Dimension 8.indb

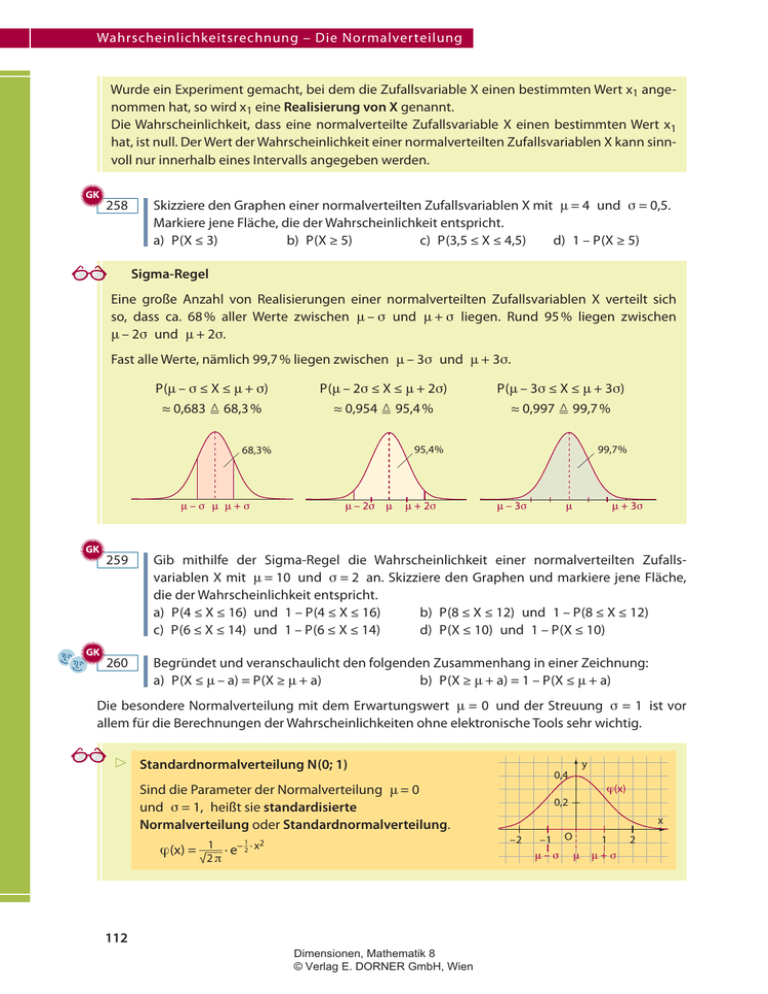
Wahrscheinlichkeitsrechnung – Die Normalverteilung
Wurde ein Experiment gemacht, bei dem die Zufallsvariable X einen bestimmten Wert x1 angenommen hat, so wird x1 eine Realisierung von X genannt.
Die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable X einen bestimmten Wert x1
hat, ist null. Der Wert der Wahrscheinlichkeit einer normalverteilten Zufallsvariablen X kann sinnvoll nur innerhalb eines Intervalls angegeben werden.
GK
258
Skizziere den Graphen einer normalverteilten Zufallsvariablen X mit Î = 4 und Ô = 0,5.
Markiere jene Fläche, die der Wahrscheinlichkeit entspricht.
a) P (X ≤ 3)
b) P (X ≥ 5)
c) P (3,5 ≤ X ≤ 4,5)
d) 1 – P (X ≥ 5)
Sigma-Regel
Eine große Anzahl von Realisierungen einer normalverteilten Zufallsvariablen X verteilt sich
so, dass ca. 68 % aller Werte zwischen Î – Ô und Î + Ô liegen. Rund 95 % liegen zwischen
Î – 2Ô und Î + 2Ô.
Fast alle Werte, nämlich 99,7 % liegen zwischen Î – 3Ô und Î + 3Ô.
P (Î – Ô ≤ X ≤ Î + Ô)
≈ 0,683 = 68,3 %
P (Î – 2Ô ≤ X ≤ Î + 2Ô)
≈ 0,954 = 95,4 %
GK
GK
99,7%
95,4%
68,3%
Î–Ô Î Î+Ô
P (Î – 3Ô ≤ X ≤ Î + 3Ô)
≈ 0,997 = 99,7 %
Ζ2Ô Î Î+2Ô
Ζ3Ô
Î
Î+3Ô
259
Gib mithilfe der Sigma-Regel die Wahrscheinlichkeit einer normalverteilten Zufallsvariablen X mit Î = 10 und Ô = 2 an. Skizziere den Graphen und markiere jene Fläche,
die der Wahrscheinlichkeit entspricht.
a) P (4 ≤ X ≤ 16) und 1 – P (4 ≤ X ≤ 16)
b) P (8 ≤ X ≤ 12) und 1 – P (8 ≤ X ≤ 12)
c) P (6 ≤ X ≤ 14) und 1 – P (6 ≤ X ≤ 14)
d) P (X ≤ 10) und 1 – P (X ≤ 10)
260
Begründet und veranschaulicht den folgenden Zusammenhang in einer Zeichnung:
a) P (X ≤ Î – a) = P (X ≥ Î + a)
b) P (X ≥ Î + a) = 1 – P (X ≤ Î + a)
Die besondere Normalverteilung mit dem Erwartungswert Î = 0 und der Streuung Ô = 1 ist vor
allem für die Berechnungen der Wahrscheinlichkeiten ohne elektronische Tools sehr wichtig.
x Standardnormalverteilung N (0; 1)
0,4
Sind die Parameter der Normalverteilung Î = 0
und Ô = 1, heißt sie standardisierte
Normalverteilung oder Standardnormalverteilung.
1
Ç(x)
0,2
x
–2
2
1
_
· e– }2 · x
Ç (x) = }
√ 2 Ñ
112
Dimensionen, Mathematik 8
© Verlag E. DORNER GmbH, Wien
y
–1
ΖÔ
O
1
Î Î+Ô
2