Versuch 1.0 Widerstand und Ohm`sches Gesetz (Materialgesetze)
Werbung

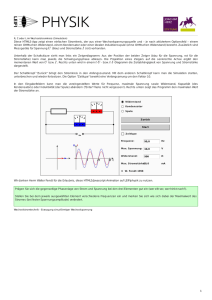
GEM, Messprogramme Versuche 0 bis 4 1/10 Versuch 1.0 Widerstand und Ohm'sches Gesetz (Materialgesetze) Lernziele Dieser Versuch wird gemeinsam mit dem Dozenten vorbereitet, durchgeführt, ausgewertet und dokumentiert. Er dient als Einführung und wird nicht benotet. • Sie kennen die Begriffe (elektrischer) Widerstand und Leitwert mit ihren Einheiten. Insbesondere können Sie unterscheiden zwischen den Bedeutungen des Begriffs Widerstand als Eigenschaft und als Bauelement. • Sie können unterscheiden zwischen den Bezeichnungen Nennwert, erwarteter Wert, "wirklicher" Wert und gemessener Wert einer physikalischen Grösse. • Sie kennen das Ohm'sche Gesetz und können es in seiner Bedeutung als Materialgesetz (konstitutives Gesetz) erläutern. • Sie können elektrische Spannungen sowie Stromstärken an einem elektrischen Bauelement (Zweipol) messen. • Sie können den elektrischen Widerstand graphisch als Kennlinie darstellen und umgekehrt aus dem Kennlinienverlauf den Widerstandswert bestimmen. • Sie können Kennlinien und Messpunkte mittels Matlab graphisch darstellen und beschriften. • Sie können den Einfluss der Temperatur auf den Widerstandswert eines Metalls qualitativ erläutern. • Sie kennen die redaktionellen und formalen Regeln zur Erstellung eines Versuchsberichts. Einleitung Der Begriff Widerstand und das Ohm'sche Gesetz Das Verhältnis zwischen der Spannung U und der Stromstärke I bei einem Zweipol1 wird elektrischer Widerstand (oder kurz: Widerstand) dieses Zweipols genannt und mit dem Symbol R bezeichnet. Das zu R inverse Verhältnis wird Leitwert genannt und mit G bezeichnet. R= U I bzw. G= I 1 = U R Der Widerstand2 (auf Englisch: resistance) ist eine Eigenschaft des Zweipols. Da diese von der Geometrie und der Materialbeschaffenheit des Zweipols abhängt, wird beim Zusammenhang zwischen U und I von einem Materialgesetz gesprochen. Einheit von R: [ R] = V = Ω (Ohm) A Einheit von G: [ G] = A = Ω −1 = S (Siemens) V Gesetz von Ohm (G. S. Ohm, 1827) Bei Metallen und bei gleichbleibender Temperatur ist U proportional zu I, d. h.: das Verhältnis U/I bzw. R ist unabhängig von der Stromstärke oder von der Spannung. Trifft dies für einen Zweipol zu, so spricht man von einem ohmschen Widerstand. 1 2 Als Zweipol bezeichnet man ein elektrisches Bauelement mit zwei Anschlüssen. Mit dem Begriff Widerstand wird auch die technische Realisierung eines Bauelements bezeichnet, dass die Eigenschaft des elektrischen Widerstands besitzt (Englisch: resistor). —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 Aufgabe 2/10 Messung der U-I-Kennlinie Messen Sie die U-I-Kennlinie3 des Widerstands mit Nennwert4 RN = 100 Ω und der maximal erlaubten Leistung Pmax = 5 W. Verwenden Sie dabei folgende Messschaltung: Im I ≈ Im + A Uq U= Um V R – Figur 0.1 Messschaltung zur Bestimmung des Widerstands (der Strom durch das V-Meter kann hier vernachlässigt werden, so dass I ≈ Im) Erhöhen Sie die Spannung stufenweise bis zum maximal erlaubten Wert: U max = Pmax R N und stellen Sie die gemessenen Punkte der Kennlinie graphisch dar. Wählen Sie zwischen 10 und 12 gleichmässig verteilten Messwerte für die gesamte Kennlinie. Hinweis: Stellen sich die Messwerte von Spannung und Stromstärke sofort nach dem Umstellen am Netzgerät ein? Auswertung Diverse mögliche Fragestellungen und Zielsetzungen Bestimmen Sie den "wahren" Widerstandswert R aus den Kennlinie. Um wieviel % weicht dieser vom Nennwert ab? Wie ändert sich der gemessene Widerstandswert in Funktion der Stromstärke? Stellen Sie den Zusammenhang graphisch dar. Kann von einem Ohm'schen Widerstand gesprochen werden? Um wieviel % schwanken die gemessenen Werte bezogen auf den ermittelten Widerstandswert? Inventar 1 Netzgerät mit einstellbarer Spannung und wählbarer Strombegrenzung (HM 8142) 2 Multimeter (HM 8011) 1 Leiste mit diversen Messwiderständen, Genauigkeit 5 %, Belastbarkeit 5 W, 100 Ω € 3 4 Unter U-I-Kennlinie versteht man eine Graphik, wo die Spannung als Ordinate (y-Achse) und die Stromstärke als Abszisse (x-Achse) dargestellt wird. Bei der I-U-Kennlinie ist es gerade umgekehrt. Der Nennwert gibt den ungefähren Wert innerhalb einer bestimmten Toleranz an (z. B. ± 5%), den der Elektrische Widerstand des Bauelements aufweist. Der exakte Wert ist nicht bekannt. —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 3/10 Versuch 1.1 Kirchhoff'sche Gesetze (Bilanzgesetze) Lernziele • Sie kennen die Kirchhoff'schen Gesetze und können den Maschen- sowie den Knotensatz in ihrer Bedeutung als Bilanzgesetze erläutern. Einleitung Knoten- und Maschensatz Jedem Punkt einer Schaltung kann ein elektrisches Potential ϕk zugewiesen werden5. Die elektrische Spannung Uij zwischen zwei beliebigen Punkten, kann so durch die Differenz der Potentiale dieser Punkte ausgedrückt werden: Bsp.: Spannung zwischen den Punkten i und j: U ij = ϕ i − ϕ j Aus der Tatsache, dass zu jedem Punkt ein eindeutiges Potential zugeordnet werden kann, ergibt sich der sogenannte Maschensatz: Die Summe der Spannungen entlang eines geschlossenen Pfades (Masche) ergibt Null. Bsp.: U1 2 + U2 4 + U4 1 = ϕ1 − ϕ 2 + ϕ 2 − ϕ 4 + ϕ 4 − ϕ1 = 0 Bemerkungen • Der Pfad kann durch eine eine beliebige Anzahl Punkte abgesteckt bzw. definiert werden. • Da die Spannung zwischen zwei Punkten ein Mass für die Energie ist, die durch das Verschieben der Einheitsladung (1 As) zwischen diesen Punkten umgesetzt wird, kann der Maschensatz aus dem Energieerhaltungssatz abgeleitet werden. In den Zweigen einer Schaltung fliessen diverse Stromstärken Ik . In den Orten (Knoten), wo Zweige zusammenkommen, kann sich keine Ladung ansammeln (Ladungsstau). Daraus folgt der sogenannte Knotensatz: Die Summe der Stromstärken in einem Knoten ergibt Null. Bsp.: I1 + I2 + I4 = 0 Bemerkungen • Bei der Bildung der Summe müssen die Bezugsrichtungen der Stromstärken berücksichtigt werden: Ströme die in einen Knoten hineinfliessen müssen ein anderes Vorzeichen aufweisen als Ströme die herausfliessen. • Kommt es in einem Gebiet (Raum) nicht zu einer Ansammlung von Ladungen, so gilt der Knotensatz für die Stromstärken durch die Grenze dieses Gebiets. Zeigen Sie durch Anwendung dieser Sätze, dass a) zwei hintereinander geschaltete (Serie- oder Reihenschaltung) Widerstände R1 und R2 durch einen einzigen Widerstand mit dem Widerstandswert R = R1 + R2 ersetzt werden können. b) zwei nebeneinander geschaltete (Parallelschaltung) Widerstände R1 und R2 durch einen einzigen Widerstand mit dem Leitwert G = G1 + G2 ersetzt werden können, d. h. 1/R = 1/R1 + 1/ R2 . 5 Diese Aussage ist analog zur Feststellung, dass in einem hydraulischen System in jedem Punkt ein bestimmter Druck zugeordnet werden kann. —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 Aufgabe 4/10 Überprüfung der Kirchhoff'schen Gesetze Erstellen Sie eine beliebige Schaltung mit Widerständen aus dem Sortiment: I2 R2 + I0 Netzgerät – I1 ϕ1 R1 ϕ2 I3 I4 R3 ϕ3 R4 I5 ϕ4 R5 Figur 1.1 Beispiel einer möglichen Schaltung mit verschiedenen Widerständen Die Knoten sind mit den Potentialen bezeichnet, die Zweige durch die Zweigstromstärken. Überprüfung des Maschensatzes Stellen Sie am Netzgerät eine geeignete Spannung ein, so dass die Belastung der Widerstände tolerierbar ist. Dazu müssen die Stromstärken und die Leistungen in den Widerständen im Voraus rechnerisch bestimmt werden! Messen Sie sämtliche Spannungen zwischen den Knotenpunkten (U1 2, U1 3, U1 4, U2 3, U2 4 und U3 4). Zeigen Sie, dass entlang eines beliebigen Pfads die Summe der Spannungen Null ergibt6. Beachten Sie dabei, dass bei einer Vertauschung der Indizes Uij = – Uji gilt. Bestimmen Sie die Potentiale der Knoten für zwei verschiedene Festlegungen des Referenzpunktes (Knoten mit Potential Null). Beispiel: U2 3 + U3 4 + U4 2 = 0 V, bzw. U2 3 + U3 4 – U2 4 = 0 V Überprüfung des Knotensatzes Bestimmen Sie die Stromstärken in den Widerständen indirekt aus den Spannungen über den Widerständen, z.B. I1 = U1 2/R1 . Zeigen Sie, dass die Summe aller Ströme die in einen beliebigen Knoten hineinfliessen der Summe der Stromstärken entspricht die herausfliessen7. Beispiele: für den Knoten 1: – I0 + I1 + I2 = 0, bzw. für den Knoten 4: – I4 – I5 + I0 = 0 addiert man die beiden Gleichungen ergibt sich: I1 + I2 – I4 – I5 = 0 (wie ist das zu verstehen?) Bemerkung: Wird die Bezugsrichtung8 einer Stromstärke umgedreht, so ändert sich das Vorzeichen der betroffenen Stromstärke. Inventar 1 Netzgerät mit einstellbarer Spannung und wählbarer Strombegrenzung (HM 8142) 2 Multimeter (HM 8011) 2 Leisten mit Messwiderständen, Genauigkeit 5 %, Belastbarkeit 5 W, verfügbare Werte: 2 × 1 Ω, 1.5 Ω, 3.3 Ω, 6.8 Ω, 10 Ω, 22 Ω, 100 Ω, 2 × 1 kΩ, 2 × 10 kΩ, 100 kΩ, 2 × 100 Ω, 2 × 330 Ω, 2 × 1 kΩ, 2 × 3.3 kΩ, 2 × 10 kΩ, 2 × 33 kΩ, 2 × 100 kΩ 6 7 8 Auf Grund der begrenzten Messgenauigkeit kann anstelle von Null ein kleiner Restbetrag übrigbleiben. Möglicherweise bis zu einem von der Mess- und Rechengenauigkeit abhängigen Restbetrag. Die Strombezugsrichtung ist willkürlich gewählt und wird in einem Schaltschema durch die Pfeilrichtung angegeben. Fliesst ein Strom in Pfeilrichtung, so ist die Stromstärke positiv, fliesst er entgegen der Pfeilrichtung, so ist sie negativ. —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 5/10 Versuch 1.2 Kennlinien aktiver Zweipole Lernziele • Sie kennen die Definitionen der Begriffe aktiver und passiver Zweipol. • Sie kennen die Begriffe ideale Spannungs- und Stromquelle und ihre Kennlinien. • Sie kennen die Begriffe lineare Spannungs- und Stromquelle und ihre Kennlinien. • Sie kennen die Begriffe Leerlaufspannung und Kurzschlussstrom. • Sie können Kennlinien von aktiven Zweipolen wie Batterien messtechnisch aufnehmen und diese durch ein lineares mathematisches Modell (lineare Kennlinie) näherungsweise beschreiben. • Sie sind in der Lage eine physikalische Ersatzschaltung (lineare Spannungsquelle, lineare Stromquelle) und deren Parameter zu ermitteln, für einen beliebigen Zweipol der eine vorgegebene lineare Kennlinie aufweist (linearer Zweipol). Einleitung Realisierung von idealen und linearen Quellen Das am Laborplatz vorhandene Netzgerät verwendet elektronische Schaltungstechniken, um das Verhalten einer nahezu idealen Spannungs- bzw. Stromquelle zu erzeugen. Für relativ hochohmige Lastwiderstände verhält sich das Gerät wie eine ideale Spannungsquelle9, deren Spannungswert Uq eingestellt werden kann. Bei relativ niederohmigen Lastwiderständen verhält sich das Gerät wie eine ideale Stromquelle10, deren Stromwert Iq eingestellt werden kann. Der Übergang vom Spannungsquellen- zum Stromquellenbetrieb geschieht beim Lastwiderstand RL=Uq /Iq . Ergänzen wir nun diese idealen Quellen mit einem externen Widerstand (Ri in der Figur 1.1, bzw. Gi in der Figur 1.2), so erhalten wir in beiden Fällen eine sogenannte lineare Quelle. Ri Im + Uq Um V A + R Gi – Figur 1.1 Lineare Spannungsquelle Iq Im Um V A R – Figur 1.2 Lineare Stromquelle Aufgabe 1 Lineare Spannungs- und Stromquellen a) Stellen Sie am Netzgerät bei Leerlauf die Quellenspannung Uq = 10.0 V ein. Schalten Sie gemäss Figur 1.1 einen Widerstand von Ri = 100 Ω in Serie zum Netzgerät. Nehmen Sie nun mit einem variablen Widerstand R die U-I-Kennlinie des somit erhaltenen Zweipols auf. Der Lastwiderstand RL des Zweipols kann aus den Messwerten Um und Im bestimmt werden: RL = Um/Im. Beschreiben Sie die erhaltene Kennlinie mathematisch in Funktion der Grössen Uq , Ri und RL. b) Stellen Sie am Netzgerät bei Kurzschluss den Quellenstrom Iq = 100 mA ein. Schalten Sie gemäss Figur 1.2 denselben Widerstand Ri wie bei der Teilaufgabe a) (Leitwert Gi = 1/Ri = 1.00·10-2 Ω-1) parallel zum Netzgerät. Nehmen Sie nun mit einem variablen Widerstand R die U-I-Kennlinie des somit erhaltenen Zweipols auf. Beschreiben Sie die erhaltene Kennlinie mathematisch in Funktion der Grössen Iq , Gi und GL = 1/RL. 9 10 Eine ideale Spannungsquelle liefert eine feste Spannung, unabhängig von der Stromstärke durch die Quelle, d. h. auch unabhängig von der Quellenbelastung. Eine ideale Stromquelle liefert eine feste Stromstärke, unabhängig von der Spannung über der Quelle, d. h. auch unabhängig von der Quellenbelastung. —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 6/10 Vergleichen Sie die Ergebnisse aus a) und b). Fragestellungen • Welche Schlussfolgerungen ziehen Sie aus diesem Vergleich? • Wie genau können die Quellenwerte Uq und Iq eingestellt werden und welchen Einfluss hat eine Abweichung im wirklichen Wert von Ri vom angenommenen Wert? Aufgabe 2 Kennlinie einer Trockenbatterie Ermitteln Sie die Kennlinie einer Trockenbatterie, indem Sie bei verschiedenen Lastwiderständen die sich einstellenden Arbeitspunkte aufnehmen (siehe Figur 1.3). Überlegen Sie im Voraus, welche Lastwiderstände in Frage kommen. Die Batterieeigenschaften sind im Abschnitt Inventar under Messobjekt zu finden. Im + A Batterie V Um R (variabel) – Figur 1.3 Schaltung zur Messung der U-I-Kennlinie einer Batterie Fragestellungen • Kann diese Kennlinie durch eine Gerade angenähert werden? Wie gut? In welchem Bereich? • Haben deren Parameter (Steigung, Schnittpunkte mit Abszisse und Ordinate) eine physikalische Bedeutung? Welche? • Wie könnte ein einfaches Ersatzschema für das elektrische Verhalten dieser Batterie gemäss der obigen Näherung aussehen? Vergleichen Sie Ihre Ergebnisse mit den Angaben aus der Literatur. Inventar 1 Netzgerät mit einstellbarer Spannung und wählbarer Strombegrenzung (HM 8142) 2 Multimeter (HM 8011) 2 Leisten mit Messwiderständen, Genauigkeit 5 %, Belastbarkeit 5 W, Werte: 2 × 1 Ω, 1.5 Ω, 3.3 Ω, 6.8 Ω, 10 Ω, 22 Ω, 100 Ω, 2 × 1 kΩ, 2 × 10 kΩ, 100 kΩ 2 Widerstandsdekaden (1 Ω … 11 MΩ), Genauigkeit 1 %, Belastbarkeit 1 W 2 Krokodilklemmen Messobjekt 1 Batterie (Typ Leclanché) 4.5 V, 3R12 Dieser Batterietyp kann für kurze Zeiten kurzgeschlossen werden. Bei einer neuwertigen Batterie kann der Kurzschlusstrom mehr als 10 A und die an 0.5 Ω abgegebene Leistung bis zu 50 W betragen! Als Lastwiderstände unbedingt 5 W-Widerstände verwenden und diese nur kurzzeitig belasten. Der Kurzschlusstrom nimmt mit dem Ladezustand der Batterie ab. Allgemein sollte die Batterie nur kurzzeitig belastet werden, da der Arbeitspunkt sonst wegdriftet. —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 7/10 Versuch 1.3 Arbeitspunkt und Leistungsanpassung Lernziele • Sie kennen die formalen Zusammenhänge zwischen Spannung, Stromstärke und (dissipierter) Leistung für einen elektrischen Widerstand. • Sie können durch Messung von Spannung und Stromstärke die Grössen (elektrischer) Widerstand und (dissipierte) Leistung bestimmen. • Sie wissen wie systematische Fehler bei simultaner Spannungs- und Stromstärkemessung zustande kommen und wissen wie diese durch geeignete Massnahmen vermindert und durch Rechnung korrigiert werden können. Sie verstehen dabei die Begriffe spannungsrichtiges und stromrichtiges Messen. • Sie kennen die elektrischen Eigenschaften der Spannungs- und Strommessgeräte: Sie kennen die Grössenordnungen ihrer Widerstandswerte und ihren Zusammenhang mit den eingestellten Messbereichen. • Sie kennen den Begriff zufälliger Fehler und die Fehlerfortpflanzungsgesetze für die elementaren Operationen Addition, Subtraktion, Multiplikation und Division. • Sie können unterscheiden zwischen relativen und absoluten Fehlergrössen. • Sie können die Begriffe Arbeitspunkt und Leistungsanpassung für eine lineare Quelle erläutern. Einleitung Systematische Messfehler Die Bestimmung eines unbekannten Widerstands kann durch simultane Messung von Strom und Spannung erfolgen. Bei Objekten mit grossen oder kleinen Widerstandswerten muss überprüft werden ob die Messgeräte nicht zu systematischen Messfehlern führen, d. h. ob die Messwerte nicht durch die Messgeräte selbst beeinflusst werden. • Spannungsrichtige Messung oder Stromfehlerschaltung, gemäss Figur 3.1 eignet sich zur Messung von Objekten mit verhältnismässig niedrigem Widerstand. Dabei wird der Strom durch das V-Meter zusammen mit dem Strom im betrachteten Objekt gemessen. Ist nun der Innenwiderstand des V-Meters in der Grössenordnung von dem des Objekts oder sogar kleiner, so ist die angezeigte Stromstärke sicher falsch. Ein Anzeichen für einen systematischen Fehler liegt dann vor, wenn sich beim Abhängen des VMeters die gemessene Stromstärke verändert. • Stromrichtige Messung oder Spannungsfehlerschaltung, gemäss Figur 3.2 eignet sich zur Messung von Objekten mit verhältnismässig hohem Widerstand. Dabei wird die Spannung über dem A-Meter zusammen mit der über dem betrachteten Objekt gemessen. Ist nun der Innenwiderstand des A-Meters in der Grössenordnung von dem des Objekts oder sogar grösser, so ist die angezeigte Spannung sicher falsch. Ein Anzeichen für einen systematischen Fehler liegt dann vor, wenn sich beim Überbrücken (Kurzschliessen) des A-Meters der gemessene Spannungswert verändert. Im I I = Im + + A A Uq Uq V – Figur 3.1 Spannungsrichtiges Messen V Um U – Figur 3.2 Stromrichtiges Messen Ohne die Korrektur des systematischen Fehlers (Rm = Um/Im) liefert die spannungsrichtige Messung einen zu kleinen Widerstandswert (Rm < R = U/I), die stromrichtige Messung hingegen einen zu grossen (Rm > R —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 8/10 = U/I). Diese systematischen Fehler können bei bekannten Innenwiderstandswerten der Messgeräte11 abgeschätzt und gegebenenfalls rechnerisch korrigiert werden. Im Allgemeinen wird die Schaltung ausgewählt, die den kleineren systematischen Fehler ergibt, so dass unter Umständen auf die Korrektur verzichtet werden kann. Ob ein systematischer Fehler überhaupt korrigiert werden muss, hängt von der gewünschten Messgenauigkeit und von den zufälligen Fehlern, bzw. der Genauigkeit der Messgeräte ab. Im Allgemeinen besitzen V-Meter hohe Innenwiderstandswerte (Grössenordnung: 1 bis 10 MΩ), so dass mit spannungsrichtigem Messen meistens (aber nicht immer!) kein nennenswerter systematischer Fehler gemacht wird. Die Innenwiderstandswerte der A-Meter nehmen mit kleiner werdendem Messbereich zum Teil stark zu (Grössenordnung: Ω bis kΩ !, je nach Bereich). Mit dem Messwertepaar Um und Im kann ebenfalls die in der Last dissipierte12 Leistung Pm bestimmt werden: Pm = Um·Im. Bei beiden Schaltungen ist der ermittelte Leistungswert auf Grund der systematischen Fehler zu gross (Pm > P = U·I). Hier aber richtet sich die Wahl der Schaltung nicht nach den systematischen Fehlern, sondern nach der Bedingung unter welcher die Leistung im Messobjekt bestimmt werden soll: z. B. die Messung der Leistung in einem Widerstand bei 12.0 V Spannung verlangt spannungsrichtiges Messen. Aufgabe 1 Bestimmung der Messfehler Messen Sie den Widerstandswert und die dissipierte Leistung eines Widerstands mit Nennwert 100 Ω bei der vorgegebenen Stromstärke von 10.0 mA und eines Widerstands mit Nennwert 1 MΩ bei der vorgegebenen Spannung von 30.0 V. Die Wahl der Messchaltungen soll es dabei ermöglichen die Randbedingungen einzustellen. Bestimmen Sie sämtliche systematische und zufällige Fehler. Aufgabe 2 Leistungsanpassung In diesem Versuch soll die von der linearen Quelle an die Last abgegebene Leistung PL in Funktion des Lastwiderstands RL untersucht werden. Bei Kurzschluss (RL = 0) und bei Leerlauf (RL = ∞) gibt die Quelle keine Leistung ab. Daher muss es einen optimalen Lastwiderstand RLopt geben, bei dem die abgegebene Leistung maximal wird. Leiten Sie den Verlauf von PL in Funktion von RL formal her und stellen Sie diese Funktion in einer halblogarithmischen Skala (logarithmisch für RL, linear für PL) graphisch dar. Bestimmen Sie theoretisch den optimalen Widerstand und die dabei abgegebene maximale Leistung PLmax. Benutzen Sie die Messwerte der Aufgabe 1 a) aus Versuch 1.2 (lineare Spannungsquelle mit Leerlaufspannung U0 = 10.0 V und Kurzschlussstrom IC = 100 mA). Bestimmen Sie die von dieser Quelle an die Last abgegebene Leistung für die diversen Arbeitspunkte, bzw. für die verschiedenen Lastwiderstandswerte. Tragen Sie diese Messwerte in die vorbereitete Graphik mit dem theoretischen Funktionsverlauf ein. Fragestellungen • In welchem Bereich darf der Lastwiderstand liegen, wenn mindestens 95% von PLmax an die Last abgegeben werden soll? • Bei welchem Lastwiderstand beträgt der Wirkungsgrad13 der Schaltung 95%? • Ergeben sich die selben Ergebnisse bei einer linearen Stromquelle? • Wie lassen sich diese Ergebnisse für beliebige lineare Quellen verallgemeinern? Inventar 1 Netzgerät mit einstellbarer Spannung und wählbarer Strombegrenzung (HM 8142) 2 Multimeter (HM 8011) 2 Widerstandsdekaden (1 Ω … 11 MΩ), Genauigkeit 1 %, Belastbarkeit 1 W 11 12 13 Das elektrische Gleichstromverhalten der Messgeräte kann durch Widerstände beschrieben werden. dissipiert: in Wärmeenergie ungesetzt Mit Wirkungsgrad versteht man hier das Verhältnis von PL (Nutzleistung = Um·Im) zur Leistung welche die ideale Quelle (hier das Netzgerät) abgibt (totale Leistung = Uq ·Im). —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 9/10 Versuch 1.4 Kennlinien einer Solarzelle Lernziele • Sie kennen die Solarzelle als ein Beispiel für einen Energiewandler (Energieumlader). • Sie kennen das Verbraucher- und das Erzeugerpfeilsystem für Spannung, Strom und Energiestrom von Zweipolen und können Kennlinien entsprechend dem Pfeilsystem umzeichnen und interpretieren. • Sie können die Begriffe aktiver, passiver, aktiv wirkender und passiv wirkender Zweipol erläutern und richtig verwenden. • Sie verstehen die Bedeutung des Begriffs Leistungsanpassung für einen nichtlinearen aktiven Zweipol und sind in der Lage den entsprechenden optimalen Arbeitspunkt zu ermitteln. Einleitung Solarzellen Solarzellen sind nichtlineare Zweipole, die sich je nach Schaltung und Lichteinfall aktiv oder passiv verhalten können14. Ohne Lichteinfall unterscheiden sie sich nicht wesentlich von gewöhnlichen Halbleiterdioden. IU-Kennlinie einer Solarzelle bei Lichteinfall 400 350 300 I Strom in mA 250 U 200 150 100 50 0 -50 -3 -2 -1 Spannung in V 0 1 Figur 4.1 I-U-Kennlinie einer Solarzelle bei Lichteinfall Bei Lichteinfall verschiebt sich ihre I-U-Kennlinie in Richtung negativer Ströme, so dass ein Teil davon in den vierten Quadranten zu liegen kommt (siehe Figur 4.1). Im ersten Quadranten weicht die Kennlinie nur wenig von jener ohne Lichteinfall ab. Im dritten Quadranten verhält sich die Solarzelle wie ein Photowiderstand (lichtabhängiger Widerstand). Im vierten Quadranten wirkt die Zelle aktiv. 14 passiv verhalten oder passiv wirken: Energie aufnehmen aktiv verhalten oder aktiv wirken: Energie abgeben —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup GEM, Messprogramme Versuche 0 bis 4 10/10 Aufgabe 1 Messen der I-U-Kennlinie einer Solarzelle im aktiven Quadranten Bei dieser Messung stellt der Lichteinfall (Strahlungsintensität, W/m2 ) einen zusätzlichen Parameter dar. Wählen Sie 2 verschiedene Lichtintensitäten, eine entsprechend der maximalen Glühlampenleistung von 25 W. Damit Ihre Messung nicht vom Umgebungslicht beeinflusst wird, müssen die Solarzelle und die Glühbirne mit einer Hülle (Kartonschachtel) abgedeckt werden. Da die Solarzelle nur bei sehr geringen Spannungen aktiv wirkt, wird ihre Kennlinie im vierten Quadranten mit folgender Schaltung ausgemessen. RL I V Um Kartonschachtel Glühlampe Netzgerät Figur 4.2 Messschaltung für Messung der Kennlinie im 4. Quadranten Für RL verwende man Widerstände zwischen 0.5 Ω und 100 Ω. Der Strom muss aus Um und RL bestimmt werden, d.h. RL muss möglicherweise noch ausgemessen werden. Hinweise: • Erklären Sie, warum hier die direkte Messung des Stromes mit einem Strommessgerät nicht geeignet ist. • Um die Polarität der Solarzelle feststellen zu können, ist vorab eine (grobe) Messung der Kennlinie ohne Lichteinfall nötig. In Vorwärtsrichtung wird die maximale Stromstärke mit einer Spannung unterhalb 1 V erreicht. Stellen Sie die beiden I-U-Kennlinien der Solarzelle in der selben Graphik dar. Aufgabe 2 Auswertung Stellen Sie für die beiden Lichtintensitäten die Solarzellenleistung in Abhängigkeit der Zellenspannung, d.h. für verschiedene Lastwiderstände, dar. Bestimmen Sie für die betrachteten Lichtintensitäten den Lastwiderstandswert, bei dem die von der Solarzelle abgegebene Leistung maximal wird (Leistungsanpassung). Sind diese optimalen Lastwiderstände in beiden Fällen gleich? Welche Leistung gibt die Solarzelle dabei pro cm2 ab? Inventar 1 2 2 2 1 Netzgerät mit einstellbarer Spannung und wählbarer Strombegrenzung (HM 8142) Multimeter (HM 8011) Widerstandsdekaden (1 Ω … 11 MΩ), Genauigkeit 1 %, Belastbarkeit 1 W Lampen (24 V, 25 W) auf Sockel Kartonabdeckung Messobjekt 1 Solarzelle auf Sockel, maximale Stromstärke in beide Richtungen: 400 mA, maximale Spannung in Sperrrichtung: 3 V —————————————————————————————————————————————————— Zürcher Hochschule Winterthur, Departement T 15. Oktober 2005, © M. Schlup