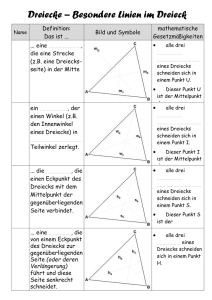
A14_Merkwürdige Punkte

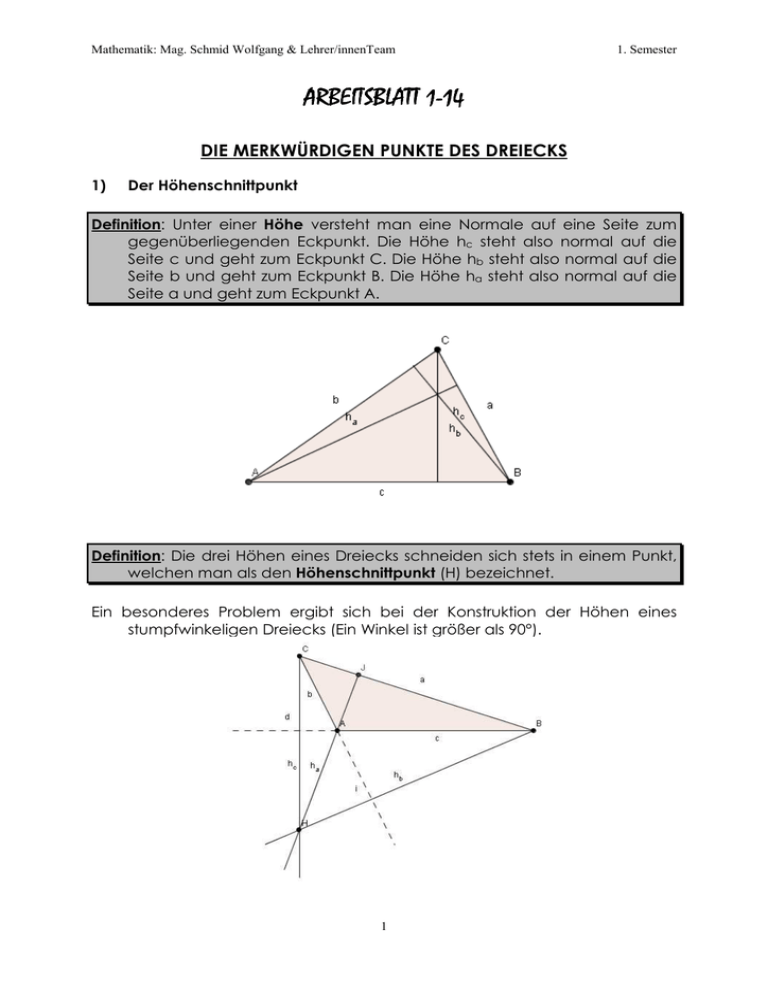
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
ARBEITSBLATT 1-14
DIE MERKWÜRDIGEN PUNKTE DES DREIECKS
1)
Der Höhenschnittpunkt
Definition: Unter einer Höhe versteht man eine Normale auf eine Seite zum
gegenüberliegenden Eckpunkt. Die Höhe hc steht also normal auf die
Seite c und geht zum Eckpunkt C. Die Höhe hb steht also normal auf die
Seite b und geht zum Eckpunkt B. Die Höhe ha steht also normal auf die
Seite a und geht zum Eckpunkt A.
Definition: Die drei Höhen eines Dreiecks schneiden sich stets in einem Punkt,
welchen man als den Höhenschnittpunkt (H) bezeichnet.
Ein besonderes Problem ergibt sich bei der Konstruktion der Höhen eines
stumpfwinkeligen Dreiecks (Ein Winkel ist größer als 90°).
1
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Wir erkennen, dass sich bei der Konstruktion der Höhe ha das Problem ergibt,
dass die Seite a zu kurz ist. Folglich müssen wir die Seite a wie benötigt
verlängern. Die Länge der Höhe ha ergibt sich durch die Distanz des
Punktes A vom Schnittpunkt der Höhe ha mit der Seite a.
Entsprechendes gilt auch für die Höhe hb.
Wenn wir aber den Höhenschnittpunkt haben wollen, so müssen wir auch
noch die Höhen verlängern.
Übungen: Übungsblatt 14; Aufgabe 240
2)
Der Schwerpunkt:
Definition: Der Schwerpunkt ist der Schnittpunkt der Schwerlinien. Eine
Schwerlinie
geht
vom
Halbierungspunkt
einer
Seite
zum
gegenüberliegenden Eckpunkt. Alle drei Schwerlinien eines Dreiecks
schneiden sich stets in einem Punkt.
Den Halbierungspunkt einer Seite wollen wir aber nicht einfach ausrechnen
und abmessen, sondern konstruieren:
A
B
Wir suchen einen Punkt, der von A gleich weit weg ist wie von B. Wir stechen
also in A mit dem Zirkel ein, stellen den Zirkel auf eine Größe über die
Hälfte der Strecke AB ein und ziehen einen Teilkreis.
A
B
Auf diesem Kreis liegen nun alle Punkte, die von A den Abstand unseres
Radius haben. Wir brauchen nun jenen Punkt auf dem Kreis, der auch
von B genau diesen Radius entfernt ist. Dazu verändern wir die Größe des
Radius nicht, stechen in B ein und schlagen ab.
2
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
S
A
B
Der erhaltene Schnittpunkt S ist gleich weit von A als auch B entfernt. Mit
anderen Radien könnten wir uns beliebig viele solcher Punkte
konstruieren. Logischerweise (Überlege!!) müssen aber alle diese Punkte
auf einer Normalen auf die Strecke AB liegen.
S
A
HAB
B
sAB
Auf dieser Geraden (sAB bezeichnet) liegen folglich alle Punkte, die von A und
B gleich weit weg sind. Man nennt eine derartige Gerade eine
Streckensymmetrale. Den Schnittpunkt der Streckensymmetrale mit der
entsprechenden Strecke nennt man den Halbierungspunkt ( HAB
bezeichnet) der Strecke.
Definition: Eine Streckensymmetrale ist die Menge aller Punkte, die zu den
Endpunkten der Strecke gleichen Abstand haben. Der Halbierungspunkt
einer Strecke ist jener Punkt auf der Strecke, der von den beiden
Endpunkten der Strecke gleichen Abstand hat.
Nun konstruieren wir bei einem gegebenen Dreieck den Schwerpunkt. Für die
Schwerlinie auf die Seite c benötigen wir zunächst den Halbierungspunkt
der Strecke; also Zirkel größer als die Hälfte der Seite c einstellen, in A
einstechen, einen Teilkreis ziehen, in B einstechen und abschlagen. Nun
das Geodreieck normal auf die Seite c anlegen und eine Normale auf c
durch den Schnittpunkt der Kreise ziehen. Der Schnittpunkt dieser
Normalen mit unserer Seite c ist der gesuchte Halbierungspunkt.
3
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
C
sc
A
HAB
B
Die
Verbindungslinie
des
Halbierungspunktes
HAB
mit
dem
gegenüberliegenden Eckpunkt C ist die Schwerlinie auf C (sc abgekürzt).
Nun konstruieren wir die Schwerlinie einer anderen Seite, z.B auf b.
C
Die dritte Schwerlinie müssen wir nicht unbedingt konstruieren, da sie ja durch
den Schnittpunkt der ersten beiden Schwerlinien gehen muss. Der
Schnittpunkt der Schwerlinien ist der Schwerpunkt.
Übungen: Übungsblatt 14; Aufgabe 241
3)
Der Umkreismittelpunkt
Definition: Der Umkreis ist ein Kreis der durch alle drei Eckpunkte eines
Dreiecks geht. Den Mittelpunkt dieses Kreises nennt man den
Umkreismittelpunkt, welcher der Schnittpunkt der Streckensymmetralen
ist.
Wir konstruieren nun also den Umkreis: Wir konstruieren zunächst einmal die
Streckensymmetrale auf die Seite c. Wie bereits beim Schwerpunkt
erklärt: Zirkel einstellen in A einstechen und Teilkreis ziehen, in B
einstechen und abschlagen. Die Normale auf die Seite c durch den
4
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Schnittpunkt der beiden Kreise ist die Streckensymmetrale auf AB (sAB
bezeichnet)
C
sAB
B
A
Nun konstruieren wir noch die Streckensymmetrale auf die Seiten a und b
(Eine würde genügen, da sich wieder alle drei Geraden in einem Punkt
schneiden).
Der
gemeinsame
Schnittpunkt
aller
drei
Streckensymmetralen ist der Umkreismittelpunkt (U). Somit können wir
auch den Umkreis einzeichnen: In U einstechen und den Zirkel bis zu
einem beliebigen Eckpunkt von der Größe einstellen.
Übungen: Übungsblatt 14; Aufgabe 242
5
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
4)
1. Semester
Der Inkreismittelpunkt
Unter dem Inkreis eines Kreises versteht man einen Kreis, der alle drei Seiten
berührt, sie aber nicht schneidet. Ein Inkreis soll also folgendermaßen
aussehen:
C
A
B
Definition: Unter einem Inkreis versteht man einen Kreis, der alle drei Seiten
des Dreiecks berührt. Den Mittelpunkt dieses Dreiecks nennt man den
Inkreismittelpunkt(I),
welcher
sich
als
der
Schnittpunkt
der
Winkelsymmetralen ergibt.
Zunächst müssen wir uns einmal klar machen, was eine Winkelsymmetrale ist
und wie man sie konstruiert.
Definition: Eine Winkelsymmetrale ist eine Gerade, die einen gegebenen
Winkel halbiert.
Nun
überlegen wir uns, wie wir diese konstruieren können: Jede
Winkelhalbierende muss natürlich durch den Scheitel des Winkels gehen.
Was wir also noch benötigen ist ein zweiter Punkt der Winkelsymmetrale.
Dies muß ein Punkt sein der von beiden Schenkeln des Winkels gleichen
Normalabstand hat.
Um diesen zu konstruieren, stechen wir mit dem Zirkel im Scheitel des Punktes
ein und ziehen einen derartigen Teilkreis so, dass beide Schenkel
geschnitten werden.
S2
S1
Nun stechen wir im ersten Schnittpunkt (S1 bezeichnet) ein, zeichnen einen
Teilkreis, verstellen den Zirkel nicht, stechen in S2 ein und schlagen ab.
6
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Der erhaltene Schnittpunkt muss folglich gleich weit von den beiden
Schenkeln entfernt sein, also ein Punkt der Winkelsymmetrale sein.
Folglich ist eine Gerade durch diesen Punkt und dem Scheitel die
Winkelsymmetrale w.
S1
w
S2
Wollen wir also den Inkreismittelpunkt konstruieren, so müssen wir die
Winkelhalbierende zweier Winkel konstruieren. Ihr Schnittpunkt ist der
Inkreismittelpunkt (Die dritte Winkelsymmetrale geht natürlich ebenfalls
durch den Inkreismittelpunkt).
Um den Inkreis aber nun einzeichnen zu können, benötigen wir noch eine
Information:
Merke: Eine berührende Gerade steht immer im rechten Winkel auf den
Radius zum Berührpunkt.
Dies bedeutet, dass wir z.B. von der Seite b aus eine Linie im rechten Winkel
zum Inkreismittelpunkt zeichnen. Die Länge dieser Strecke ist der Radius
des Inkreises (r bezeichnet).
Übungen: Übungsblatt 14; Aufgabe 243
7
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
5)
1. Semester
Die EULER´sche Gerade
Satz: Höhenschnittpunkt, Schwerpunkt und Umkreismittelpunkt eines Dreiecks
liegen immer auf einer Geraden; diese nennt man die Euler´sche
Gerade.
Übungen: Übungsblatt 14; Aufgabe 244
Der Maßstab
Viele Figuren oder Pläne wie dieser Wohnungsplan oben können nicht direkt
gezeichnet werden, da die Längenangaben zu groß sind. Man hilft sich ab,
indem man die tatsächlichen Größen so verkleinert, dass eine Zeichnung
möglich ist. Das Ausmaß der Verkleinerung muss aber immer angegeben sein,
da man ja von den messbaren Zeichnungsgrößen umgekehrt wieder auf die
realen Größen zurückrechnen können muss. Das Maß der Verkleinerung nennt
man den Maßstab.
8
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
In unserem obigen Beispiel ist der Maßstab 1: 100. Dies bedeutet, dass 1 cm
auf dem Plan 100 cm in der Wirklichkeit entsprechen. Messen wir also auf der
Zeichnung eine Länge, so müssen wir sie mit 100 multiplizieren, um die
tatsächliche Länge zu wissen. Umgekehrt müssen wir eine tatsächliche Länge
durch 100 dividieren, um sie am Plan einzeichnen zu können.
⋅ 100
PLAN
WIRKLICHKEIT
: 100
Beispiel: Ein Plan hat den Maßstab 1: 50. Eine Linie misst 5 cm. Wie lang ist
diese Strecke real?
Lösung: 5 ⋅ 50 = 250cm = 2,5m
Übungen: Übungsblatt 14; Aufgaben 245 - 248
9