1. Zahlenbereiche - Fakultät für Mathematik

Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
51 722 Elementarmathematik (LH)
1.
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
und Fehlerfreiheit
Zahlenbereiche
1.2. Die ganzen Zahlen
1.2.1. Zahlenbereichserweiterung
In der Schulmathematik erfolgt eine Zahlenbereichserweiterung dann, wenn bestimmte Rechenoperationen in der bereits bekannten Zahlenmenge nicht durchführbar sind. Man spricht von der so
genannten Nichtabgeschlossenheit einer Zahlenmenge hinsichtlich einer bestimmten Rechenoperation.
a, b ∈ IN,
aber a D b ∉ IN
Beispiel: Die Operation 5 – 8 ist in IN nicht abgeschlossen
1.2.2. Der Begriff der Äquivalenzklasse
Die ganzen Zahlen werden als Äquivalenzklasse definiert.
Man spricht von einer Äquivalenzklasse, wenn folgende drei Eigenschaften innerhalb den Elementen einer Menge gelten:
• Reflexivität: a ~ a
Jedes Objekt ist zu sich selbst äquivalent.
• Symmetrie: a ~ b
⇔ b~a
Wenn a zu b äquivalent ist, dann ist auch b äquivalent zu a (und umgekehrt).
• Transitivität: a ~ b
und
b~c
⇒
a~c
Wenn a zu b äquivalent und b zu c äquivalent ist, dann ist a äquivalent zu c.
Ein Beispiel: Betrachten wir die Menge aller Nutztiere in einem landwirtschaftlichen Betrieb.
Wir definieren eine Relation und sagen: Zwei Tiere stehen in Relation zueinander, wenn sie von
derselben Art sind.
Das Pferd Silli zum Beispiel steht mit dem Pferd Bruno in Relation, aber nicht mit dem Huhn Kleinei. Diese Relation ist eine Äquivalenzrelation: Jedes Tier ist von derselben Art wie es selbst ist
(Eigenschaft der Reflexivität). Ist ein Tier von derselben Art wie das andere, dann ist das andere
auch von derselben Art wie das eine (Eigenschaft der Symmetrie). Wenn Silli und Karo von derselben Art sind und Silli und Bruno, dann sind auch Silli und Karo von derselben Art (Eigenschaft der
Transitivität), also alle drei Lebewesen sind Pferde.
Eine Äquivalenzklasse besteht hier also aus den Tieren einer Art. Zum Beispiel bilden auch Hühner
eine Äquivalenzklasse oder die Rinder eine andere Äquivalenzklasse.
1.2.3. Definition der ganzen Zahlen
a) Während das Teilen im praktischen Rechnen zwangsläufig zu Brüchen führt, die als Gegenstände des Rechnens und damit als „Zahlen“ empfunden werden, gilt dies für ein Ergebnis einer
Subtraktion a – b mit a < b nicht.
Aus 5 € – 8 € folgt nicht notwendigerweise, dass „3 € Schulden“ gleichzusetzen ist mit der negativen Zahl –3.
b) Ist die Menge der natürlichen Zahlen gegeben, dann lassen sich die ganzen Zahlen daraus
konstruieren:
Wir betrachten die Menge IN × IN aller Paare (a; b) natürlichen Zahlen und definieren folgende
Äquivalenzrelation:
(a, b) ~ (c, d)
falls a + d = c + b
mit a, b, c, d ∈ IN
(5, 9) ~ (6, 8)
da 5 + 9 = 6 + 8
⇔
5–8=6–9
Die Zahlenpaare (5, 9) und (6, 8) definieren also die Eigenschaft einer Äquivalenzklasse. Alle
Zahlenpaare mit dieser Eigenschaft legen eine Äquivalenzklasse fest, hier die Zahl –3.
–3 = {(1; 4); (2; 5); (3; 6); . . .}
Auf diese Weise erhalten wir beliebig viele neue Zahlen. Wir bezeichnen sie als negative ganze
–
Zahlen und schreiben ZZ .
Im Bereich der Schulmathematik wird die Notwendigkeit der Zahlenbereichserweiterung meist
mit der Nichtabgeschlossenheit der Subtraktion in IN begründet.
c) Will man an die Erfahrungswelt der Schüler anknüpfen, so kann man verschiedene Konzepte
verwenden.
ca)
Das Temperaturkonzept
cb)
Das Schuldenkonzept
cc)
Das Höhenkonzept
cd)
Das Schrittkonzept
Allen diesen Konzepten gemeinsam ist, dass sie bestimmten in der Natur oder dem Alltag
vorkommenden Ereignissen durch ein Minuszeichen eine bestimmte Vereinbarung zuordnen, die zur Unterscheidung einer entgegen gesetzten Vereinbarung dient. Als Vorarbeit
(Propädeutik) oder Modell zur Rekonstruktion von Wissensdefiziten beim Rechnen in ZZ erscheinen diese Konzepte geeignet.
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
1.2.4. Das Permanenzprinzip
Eine neue Zahlenmenge soll möglichst so definiert sein, dass die in den bisher bekannten Zahlenmengen gültigen Definitionen weiterhin Gültigkeit haben. Das Permanenzprinzip ist kein Gesetz im
strengen mathematischen Sinn, da es nicht logisch begründet werden kann und auch kein Axiom
darstellt. Am Besten versteht man es als zweckmäßige Vereinbarung.
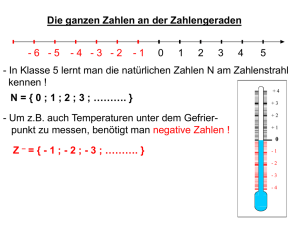
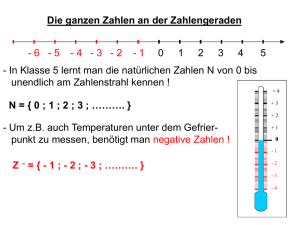
1.2.5. Einordnung der natürlichen Zahlen
–
Die Elemente der neuen Zahlenmenge ZZ ordnen wir sinnvoller Weise auf der Zahlenhalbgeraden
links von der Null an. Die Zahlenhalbgerade wird damit zur Zahlengerade. Wegen des Permanenzprinzips behalten wir die aus der Definition und Anordnung der natürlichen Zahlen bekannten Eigenschaften bei. Das sind
1. die gewählte Skalierung
2. die Kleinerbeziehung
–10
–5
0
5
10
Aus dem Permanenzprinzip folgt also beispielsweise, dass –3 < –2.
Als Äquivalenzklasse lässt sich beispielsweise auch +3 = {(4; 1); (5; 2); (6; 3); . . .} festlegen. Die
+
auf diese Weise festgelegte Zahlenmenge ZZ nennen wir positive ganze Zahlen. Ausgehend von
–
den zugrunde gelegten Definitionen von ZZ und IN ist die mathematische Natur etwa der Zahlen
+3 und 3 zu unterscheiden. Da es aber sinnvoll erscheint, die positiven Zahlen entsprechend dem
Permanenzprinzip auf der Zahlengeraden wie in der Zahlenmenge IN üblich anzuordnen, wird häu+
fig nicht zwischen den Elementen der Zahlenmenge IN und ZZ unterschieden.
+
–
IN ⊂ ZZ
Es gelten folgende Beziehungen: ZZ ∪ ZZ = ZZ
1.2.6. Größenbereich
In der Schulmathematik versteht man unter einem Größe z ein positives reelles Vielfaches n (Maßzahl) einer Einheit e. Daraus folgt, dass gilt z = n ⋅ e.
Beispiel:
n=3
e=1m
z=3⋅1m=3m
Größen dienen im Bereich der Schulmathematik zur Beschreibung alltagsbezogener Situationen.
Negative Zahlen können hierzu nach Definition nicht verwendet werden.
1.2.7. Unterrichtsspezifische Anmerkungen
a)
Das Pfeilmodell
Positive Zahlen werden durch einen Rechtspfeil, negative Zahlen durch einen Linkspfeil
dargestellt. Jedem Rechtspfeil entspricht eine Zahl auf der Zahlenhalbgeraden. Ordnen wir
auch jedem Linkspfeil eine Zahl zu, so erweitern wir unsere Zahlenhalbgerade nach links
zur Zahlengeraden.
Linkspfeile
–1
Rechtspfeile
+1
–2
+2
–3
+3
–4
+4
Bildpunkt
–4
–3
–2
–1
0
1
2
3
4
Die Zeichen "+" und "–" legen die Richtung der Zahlenpfeile bzw. die Lage der Zahlenbilder
bezüglich des Nullpunktes fest. Man nennt sie Vorzeichen der Zahlen. Das Vorzeichen gibt
also an, ob die Zahl positiv oder negativ ist.
b)
Zahl und Gegenzahl
Zwei Zahlen, deren Zahlenpfeile sich nur durch die Richtung
unterscheiden, nennt man Zahl und Gegenzahl. So ist die Zahl
–3 die Gegenzahl zu 3 und umgekehrt ist die Zahl 3 die Gegenzahl zu –3.
Zahl
Gegenzahl
–6
+6
–4
+4
5
–5
+8
–8
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
c)
und Fehlerfreiheit
Vorzeichenregeln
Wir kennzeichnen die Bildung der Gegenzahl durch ein Minuszeichen.
Gegenzahl zu
–3 ist –(–3)
Gegenzahl zu
+3 ist –(+3)
– (+3) = –3
– (–3) = +3 = 3
Gegenzahl zu
–3 ist +3
d)
Gegenzahl zu
+3 ist –3
Addition (Spitze-Fuß-Verknüpfung) und Subtraktion (Spitze-Spitze-Verknüpfung) in ZZ werden durch das Pfeilmodell veranschaulicht.
Wir veranschaulichen die Subtraktion zweier Zahlen am Pfeilmodell.
An die Spitze des ersten Pfeils wird die Spitze des zweiten Pfeils angesetzt. Der Ergebnispfeil reicht vom Fuß des Minuenden bis zum Fuß des Subtrahenden.
6
Spitze
Minuend
4
6–2=4
3
Spitze
Ergebnispfeil
0
e)
1
2
Subtrahend
3
4
5
6
7
8
9
Betrag einer Zahl
Die Maßzahl der Länge eines Zahlenpfeils heißt – ungeachtet seiner Richtung – Betrag der
Zahl.
Wir schreiben | a |. Also gilt:
|a|
| a | = –a
|a|=0
|a|=a
wenn a < 0
wenn a = 0
wenn a > 0
1.2.8. Addition von ganzen Zahlen
a)
Addition bei gleichen Vorzeichen
1.
Man addiert die Beträge.
2.
Man ordnet der Summe der Beträge das gemeinsame Vorzeichen zu.
(+a) + (+b) = +(a + b)
(–a) + (–b) = –(a + b)
a, b > 0
b)
Addition bei verschiedenen Vorzeichen
Der Ergebnispfeil ist so lang wie der Unterschied der beiden Pfeile. Er hat auch die gleiche Richtung wie der längere Pfeil. Also gilt:
1. Man subtrahiert den kleineren Betrag vom größeren Betrag.
2. Man ordnet dem Differenzwert das Vorzeichen der Zahl mit dem größeren Betrag zu.
(+a) + (–b) = +(a – b)
(–a) + (+b) = –(a – b)
a, b > 0
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
1.2.9. Subtraktion von ganzen Zahlen
Die Subtraktion einer Zahl kann durch die Addition der Gegenzahl ersetzt werden. Wir beachten die bekannten Verknüpfungsregeln und unterscheiden:
1. Fall:
Subtrahend positiv
2. Fall:
(+4) – (+3) = +1
S-S-Verknüpfung
+4
+1
0
1
2
Subtrahend negativ
(+4) – (–3) = +7
+4
–3
+3
3
4
5
6 7
0
1
2
+7
3
4
5
6
7
Die Addition der Gegenzahl führt zum gleichen Ergebnis.
Vergleiche:
(+4) – (+3) = +1
(+4) – (–3) = +7
Addition der Gegenzahl
Addition der Gegenzahl
(+4) + (–3) = +1
(+4) + (+3) = +7
Subtraktion einer Zahl
Addition der Gegenzahl
(+4) + (+3) = +7
S-S-
(+4) + (–3) = +1
+4
+4
+3
–3
+1
0
a – (+b) = a + (–b)
1
2
3
4
5
6 7
a – (–b) = a + (–b)
0
1
2
a ∈ ZZ
+7
3
4
5
6
7
b ∈ IN0
Anmerkungen: Das Ersetzen der Subtraktion einer Zahl durch die Addition einer Gegenzahl
ist unabhängig davon, ob der Minuend positiv oder negativ ist.
Jede Differenz kann als Summe geschrieben werden. Wir sprechen deshalb auch dann von
algebraischen Summen, wenn das Rechenzeichen "minus" auftritt.
Vereinfachung der Schreibweise
Bei positiven Zahlen dürfen Klammer und Vorzeichen weggelassen werden, das Rechenzeichen muss geschrieben werden.
Bei negativen Zahlen fassen wir Vorzeichen und Rechenzeichen zusammen: Sind sie
gleich, zu einem Plus-Zeichen, sind sie verschieden, zu einem Minus-Zeichen.
(+a) + (+b) =
(+a) – (+b) =
a+b
+a – b
(+a) + (–b) =
(+a) – (–b) =
a–b
a+b
Ist die erste Zahl negativ, so wird die Klammer weggelassen, das Vorzeichen wird beibehalten.
1.2.10. Multiplikation und Division in ZZ
Bei der Multiplikation zweier Zahlen gibt es vier Möglichkeiten, die Vorzeichen zu kombinieren. Die Multiplikation in ZZ können wir als verkürzte Addition gleicher Summanden ansehen. Wir betrachten zuerst die Fälle, bei denen der 1. Faktor eine positive Zahl ist.
1. Fall:
also:
(+3) ⋅ (+4)
3 ⋅ (+4)
(+4) + (+4) +(+4)
(+3) ⋅ (+4)
=
=
= +12
= +12
2. Fall:
also:
(+3) ⋅ (–4)
3 ⋅ (–4)
(–4) + (–4) +(–4)
(+3) ⋅ (–4)
Ist der erste Faktor eine negative Zahl, so kann man nicht wie oben vorgehen.
=
=
= –12
= –12
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
3. Fall: (–3) ⋅ (+4) =
Wir fordern die Gültigkeit des
Kommutativgesetzes der Multiplikation (Permanenzprinzip).
(–3) ⋅ (+4) =
(+4) ⋅ (–3) = –12
also:
(–3) ⋅ (+4) = –12
und Fehlerfreiheit
4. Fall: (–3) ⋅ (–4) =
Wir fordern die Gültigkeit des
Distributivgesetzes und betrachten den
Term (–3) ⋅ 0 mit dem Termwert 0.
Wir schreiben statt (–3) ⋅ 0:
(–3) ⋅ [(–4)
+ (+4)]
=0
(–3) ⋅ (–4)
+ (–3) ⋅ (+4) = 0
(–3) ⋅ (–4)
– 12
=0
+12
– 12
=0
also:
(–3) ⋅ (–4) = +12
1.2.11. Fachsprachliche Anmerkungen zu ZZ
1.2.12. Aufbau eines Zahlensystems
Je nach Gültigkeit bestimmter Gesetze bzw. Vorhandensein bestimmter Eigenschaften lassen sich
besondere Eigenschaften einer Zahlenmenge festlegen.
Einfache
VerknüpDoppelte
Verknüpfung
a, b, c, d
(1)
a°b=c
(2)
a ° (b ° c) = (a ° b) ° c)
(3)
a°e=e°a=a
(4)
a–1 so, dass a–1 ° a = e
(5)
a°b=b°a
Ist die bisherige Verknüpfung additiv, so gilt
für eine zweite multiplikative Verknüpfung
(2’)
a • (b • c) = (a • b) • c
(3’)
a • e’ = e’ • a = a
(6)
a • (b ° c) = a • b ° a • c
(b ° c) • a = b • a ° c a
(5’)
a•b=b•a
(4’)
a–1 so, dass a–1 • a = e
Menge
Bereich
Gruppe
Abel-Gruppe
Ring
Kommutativer Ring
Körper
1.2.13. Kulturhistorische Anmerkungen
Negative Zahlen als Schulden
Schon in einem Rechenbuch von Leonardo von Pisa (1180 – 1250 n. Chr.) findet sich eine
Rechenaufgabe über die Aufteilung eines Geldbetrages, die nur lösbar ist, wenn man negative
Zahlen, verstanden als Schulden, zulässt.
Rechnen mit negative Zahlen
Michael Stifel (1487 – 1587) war wohl einer der ersten Mathematiker, der es sinnvoll fand, mit
negativen Zahlen zu rechnen. Hierzu stellte er Rechenregeln auf, die auch heute noch Gültigkeit
haben.
So taucht um 1450 in einem Rechenbuch des Mathematikers Nicolas Chuquet der Begriff "mit plus
und minus zusammengesetzte Zahlen" auf, mit denen er rechnet.
Seine Aufgabe:
"Ich will fünf Zahlen finden, die zusammen ohne die erste 120 ergeben, ohne die
zweite 180, ohne die dritte 240, ohne die vierte 300 und ohne die fünfte 360".
Seine Lösung:
Addition dieser fünf Zahlen
120 + 180 + 240 + 300 + 360 = 1200
Division des Summenwertes durch 4
1200 : 4 = 300
Subtraktion der fünf Zahlen
300 – 120 = 180
300 – 180 = 120
300 – 240 = 60
300 – 300 = 0
300 – 360 = –60
Dagegen konnte sich John Wallis (1616 – 1703) negative Zahlen nur als Schritte in die
"Gegenrichtung" zur positiven Richtung vorstellen.
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
51 722 Elementarmathematik (LH)
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
und Fehlerfreiheit
Anerkennung der negativen Zahlen
Auch wenn man insbesondere in kaufmännischen Fragen ein Vorverständnis negativer Zahlen
entwickelte, dauerte es bis in das 17. Jahrhundert, bis man in der Mathematik vom Sinn der neuen
Zahlenmenge der negativen Zahlen überzeugt war.
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
51 722 Elementarmathematik (LH)
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
und Fehlerfreiheit
1.2.14. Übungsblatt: Zahlenbereiche – Ganze Zahlen
Aufgabe 1
1. Veranschaulichen Sie mit Zahlenpfeilen. Wählen Sie einen geeigneten Maßstab.
a) 8 – 3
b) 5 – (+2)
c) 9 – 8
d) (–24) – 12
e) (–18) – (–15)
f) (–22) + 17
g) –85 + (+45)
h) 80 – 25
i) 110 + 75
Aufgabe 2
2. Aufgabe nach Stifel:
"Ich will fünf Zahlen finden, die zusammen ohne die erste 120 ergeben,
ohne die zweite 180, ohne die dritte 240, ohne die vierte 300 und ohne
die fünfte 360".
Aufgabe 3
3. Überprüfen Sie an einem Zahlenbeispiel, ob die Menge ZZ ein Körper ist.
Aufgabe 4
4.0
4.1
4.2
4.3
Gegeben ist folgendes Schaubild.
Welche Zahlen sind dargestellt?
Ergänzen Sie die fehenden Zahlenpaare.
Begründen Sie, warum die gezeichneten
Halbgeraden zu Geraden ergänzt werden
können.
4.4 Welche Voraussetzungen sind nötig,
damit Punkte auf den Gerden markiert
werden können ?
(1; 3)
(4; 3)
(3; 2)
(2; 1)
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
Lösungen zu 1.2.14
Zu Aufgabe 1
a)
Es gibt zwei Möglichkeiten:
8 – 3 = (+8) – (+3) = (+8) + (–3) =
+8
+5
+3
1. Möglichkeit
5
0
8
+8
+5
–3
1. Möglichkeit
0
5
8
Zu Aufgabe 2
Addition dieser fünf Zahlen
120 + 180 + 240 + 300 + 360 = 1200
Division des Summenwertes durch 4
1200 : 4 = 300
Subtraktion der fünf Zahlen
300 – 120 = 180
300 – 180 = 120
300 – 240 = 60
300 – 300 = 0
300 – 360 = –60
Zu Aufgabe 3
Bedingung für Körper ist die Existenz eines inversen Elements der multiplikativen Verknüpfung.
a ⋅ n = 1 mit a ∈ ZZ und n ∉ ZZ
Also ist ZZ kein Körper.
Zu Aufgabe 4
4.1
4.2
4.3
4.4
Dargestellt sind differenzgleiche Zahlenpaare.
vgl. Zeichnung
Man verwendet ZZ .
Subtraktion in ZZ .
(1; 3)
(4; 3)
(3; 2)
(2; 1)
(1; 0)
(0; –1)
(–1; –2)
(–2; –3)