Das Fermat-und Lehman-Verfahren zur Faktorisierung - T

Karl Schwalen
6.06
Version 10.12
Weitere Aufsätze des Verfassers unter http://www.primath.homepage.t-online.de
Das Fermat-Verfahren u. das Lehman-Verfahren zur Faktorisierung
Die Basis-Algorithmen sowie Varianten zu deren Optimierung
Inhaltsübersicht
Seite
1. Das Fermat Verfahren
1.1 Grundlagen und Basis-Algorithmen
1.2 Kenngrößen des Verfahren
....
....
....
....
....
....
....
....
....
....
....
2
4
2.
2.1
2.2
2.3
Restklassen-Restriktionen
Unterscheidung nach Restklassen mod 8
....
Einschränkung der Lösungsmenge
....
....
Bestimmung optimaler Moduln / Quadratfilter ....
....
....
....
....
....
....
....
....
....
6
8
10
3.
3.1
3.2
3.3
Verwendung von Vorfaktoren
Beschreibung der Wirkungsweise
fester Vorfaktor ....
....
....
variable Vorfaktoren
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
14
16
18
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
22
22
23
24
Anlage 1
Zur Lösungsanzahl von x2 – n ≡ y2 mod m ....
....
.... nach Seite 26
4. Das Lehman-Verfahren
4.1
4.2
4.3
4.4
Der Basis-Algorithmus ....
Optimierungsmöglichkeiten
Der „Spitzendetektor“ ....
Aussieben geeigneter Faktoren
....
....
....
....
Anhang 1
Zum Lösungsansatz 2k–2 ⋅ x 2 + a⋅x –
n+r
2
k
= 2k–2 ⋅ y 2 + b⋅y
Anhang 2
Programm für den seriellen Einsatz von Vorfaktoren
Anhang 3
Vergleich Lehman Verfahren versus Spitzendetektor
1
Vorbemerkung:
Die hier angesprochenen Methoden (im wesentlichen das Fermat- und das daraus entwickelte
Lehman-Verfahren), die die Zerlegung einer ganzen Zahl durch deren Darstellung als
Differenz zweier Quadratzahlen bewerkstelligen, werden heute meist nur noch aus Gründen
der historischen Vollständigkeit am Rande behandelt. Die im Zusammenhang mit der
Kryptografie auf diesem Gebiet betriebene Forschung hat inzwischen zu ungleich
leistungsfähigeren Faktorisierungs-Verfahren geführt. Da aber auch die meisten der neueren
Methoden indirekt darauf fußen, erscheint es nicht gänzlich uninteressant, die
mannigfaltigen Optimierungsmöglichkeiten dieses elementaren Verfahrens ausführlicher
darzustellen.
Es wird dabei aufgezeigt, wie sowohl das Fermat- als auch das Lehman-Verfahren sich
gegenüber den Standard-Algorithmen wesentlich leistungsfähiger gestalten lassen.
1. Fermat-Verfahren
1.1 Grundlagen
Ausgangspunkt ist das Binom x2 – y2 = (x – y)⋅(x + y) [= t1⋅t2 = n]
(1.∗)
Die Darstellung einer ganzen Zahl als Differenz zweier Quadratzahlen liefert also zugleich
das Teilerpaar (x + y, x – y) der betr. Zahl.
Welche Zahlen besitzen eine solche Darstellung?
In der Identität [n =] t1⋅t2 = (
t1 + t 2 2
)
2
−(
t1 − t 2 2
)
2
müssen – wie der Vergleich mit (1.∗) zeigt –
die beiden Klammerterme ganzzahlig sein. Das ist der Fall, wenn die ganzen Zahlen t1 und t2
beide gerade oder beide ungerade sind, da ihre Summe bzw. Differenz nur dann durch 2
teilbar ist. Sind beide Teiler ungerade, ist auch n ungerade; sind dagegen beide gerade, ist ihr
Produkt n durch 4 teilbar. Ungerade Zahlen besitzen daher für jedes Teilerpaar eine
Darstellung als Differenz zweier Quadrate; gerade Zahlen dagegen nur für die Teilerpaare, bei
denen Teiler und Komplementärteiler beide gerade sind. Zahlen der Form n ≡ 2 mod 4 lassen
sich aus diesem Grund nicht als Quadrate-Differenz schreiben.
Für die triviale Zerlegung (einer ungeraden Zahl) n = 1⋅n ist wegen x – y = 1 und x + y = n
stets x = (n+1)/2 und y = (n – 1)/2. Ist dagegen n eine Quadratzahl, erhält man die unteren
Grenzen von x und y aus n = x2 – 02 zu x = n und y = 0. Während der kleinere Teiler t1 nur
im Intervall [1, n ] zu suchen ist, können x und y also beinahe im gesamten Bereich von 0
bis n/2 auftreten! Um auf der Basis von (1.∗) dennoch zumindest für Zahlen mit einem Teiler
t1 , der nur (relativ) wenig kleiner als n ist, zu einem brauchbaren Verfahren zu kommen,
ging bereits Fermat so vor, dass er – ausgehend von u =  n  – in der Gleichung m = u2 – n
den Wert von u sukzessive erhöhte und dann jeweils prüfte, ob m ein Quadrat war. Ist m ein
solches, hat man mit u – m einen Teiler von n gefunden. Somit erhält man als
2
Basis-Algorithmus Fermatverfahren
Eingabe: n (n mod 4 ≠ 2)
u = Int(Sqr(n)): m = u^2 – n: w = 0
(*) Do While w ^2 <> m
u = u + 1: m = u^2 – n: w = Int(Sqr(m))
Loop
Ausgabe: Teilerpaar t1 = u – w, t2 = u + w
If u – w > 2 Then w = – n: Goto (*)
Mittels der (eigentlich nicht zur Basis-Variante gehörenden) letzten Zeile liefert der
Algorithmus alle Teilerpaare einer ungeraden Zahl; für durch 4 teilbare Zahlen jedoch nur die
Teilerpaare, bei denen Teiler und Komplementärteiler gerade sind.
Gibt man anstelle der Zahl n die Eingabe 4⋅n vor, so erhält man auch im Falle eines geraden n
(einschließlich n mod 4 = 2) alle Teilerpaare, wobei die beiden Ausgabewerte (u – w) bzw.
(u + w) jeweils durch 2 zu teilen sind.
Da im obigen Alg. u ab u =  n  die Folge der Quadratzahlen durchläuft, und die Differenz
zweier benachbarter Quadratzahlen (u + 1) 2 – u 2 = 2u + 1 ist, lässt sich die fortlaufende
Berechnung von u 2 – n vermeiden:
Eingabe: n (n mod 4 ≠ 2)
u = Int(Sqr(n)): m = u^2 – n: w = 0
Do While w ^2 <> m
m = m + 2*u + 1: w = Int(Sqr(m)): u = u + 1
Loop
Ausgabe: Teilerpaar t1 = u – w, t2 = u + w
Eine dritte Variante des Basis-Algorithmus kommt innerhalb der While – Loop-Schleife
gänzlich ohne Multiplikationen und Wurzelberechnungen aus:
Eingabe: n (n mod 4 ≠ 2)
u = Int(Sqr(n)): r = n – u^2: v = 2*u + 1: w = 1
Do While r > 0
Do While r < v
r = r + w: w = w + 2
Loop
r = r – v: v = v + 2
Loop
Ausgabe: Teilerpaar t1 = (v – w) / 2 , t2 = (v + w – 2) / 2
Die Haupt-Schleife wird in den drei Varianten gleich oft durchlaufen. Bei der letztgenannten
wird die innere Schleife je Durchlauf der Haupt-Schleife während der ersten Schritte des
Verfahrens allerdings mehrfach durchlaufen. Experimentell findet man, dass die dritte
Variante etwa erst ab einem Teilerverhältnis t 2 / t1 > 4 zeitliche Vorteile bringt. (Eine das
berücksichtigende Anwendung nebst Erläuterung siehe Ziffer 2.)
Zunächst werden nun einige Kenngrößen des Verfahrens abgeleitet.
3
1.2 Kenngrößen des Verfahren
•
Abhängigkeit der ’Schrittzahl’ i (Anzahl der zu prüfenden Differenzen u2 – n bis
ein Quadrat gefunden wird) vom Teilerverhältnis.
Es sei wiederum n = t1⋅t2 mit t1 < t2 . Dann ist t1 = x – y = x –
t2 = x +
x 2 − n . Damit erhält man eine Gleichung für das Teilerverhältnis v = t2 / t1.
Die Auflösung dieser Gleichung nach x führt auf x =
x=
v +1
2⋅ v
⋅ n . Da die Suche bei
 n  +1 beginnt, besteht zur Schrittzahl die Beziehung i = x –  n . Daraus

1
n  . Au
i = ( v +
− 2)⋅
 +1
2
v


folgt
Wegen
•
x 2 − n und
v=
t2
t1
und
n=
(1.∗∗)
t 1⋅t 2 ist das gleichwertig mit i =
t1 + t 2
−
2
 n .
Länge (si) des i-ten Schrittes
Unter der ’Länge des i-ten Schrittes’ wird hier die Größe des Intervalls bezeichnet, in
dem der Teiler t 2 liegen kann, wenn er im i-ten Schritt des Basis-Alg. gefunden wird.
Wie aus (1.∗∗) ersichtlich, kann v infolge der Rundungsvorschrift in einem gewissen
Umfang variieren ohne dass i sich ändert. Auflösen des Rundungsterms nach v ergibt
für io = i – 1 = const.:
t2 =
n + io ±
v = n + io ±
2 io n + io
2
2 i o n + i o ) / n bzw.
2
. Im 1. Schritt (io = 1) wird genau dann ein Teiler von n
gefunden, wenn n +1 ≤ t 2 < n + 1 + 2 n + 1 .(Wegen t 2 > t 1 ist t2 min = n +1
d.h. in diesem Fall ist nur das positive Vorzeichen vor dem Wurzelterm gültig.)
Damit ist im Sinne der obigen Definition s 1 = 2 n + 1 ≈ 2 ⋅4 n .
Wurde also im 1. Schritt kein Teiler gefunden, besitzt n im Bereich zwischen
1 + n und 1 + n + 2 ⋅4 n keinen Teiler.
Für den i. Schritt folgt (solange die Voraussetzung ’i sehr viel kleiner n ’ erfüllt ist),
durch Bildung der Differenzen analog si ≈ ( 2⋅i − 2⋅(i −1) ) ⋅ 4 n [= r⋅ 4 n ].
Nachstehend sind einige Werte des Faktors r von
i = 1:
2:
3:
4:
100:
r = 1,41...
0,58...
0,45...
0,37...
0,07...
4
n angeben:
(100%)
( 41%)
( 32%)
( 26%)
( 5%)
Die Tabelle verdeutlicht, wie schnell das Verfahren mit zunehmender Schrittzahl
uneffektiv wird. Andererseits ist die Länge von Schritt 1 durchaus bemerkenswert:
4
Beispiel: n = 10 100 ==> s1 = 1,41⋅ 10 25 D.h. mit einer einzigen Schleife des BasisAlgorithmus lassen sich mehr als 10 24 potentielle (ungerade) Teiler ausschließen, bzw.
lässt sich ein in diesem Bereich vorhandener Teiler feststellen.
Im Intervall [10 50, 1050 + 1,41⋅ 1025 ] gibt es immerhin etwa s1 / ( ln(1050) + 1) ≈
1,2⋅ 1023 Primzahlen.
Mit den obigen Formeln lässt sich auch der „praktische“ Anwendungsbereich des Verfahrens
angeben: Nimmt man an, aus Gründen der zeitlichen Beschränkung sei die maximale
Schrittzahl auf i = 10 9 begrenzt, so ergeben sich abhängig vom Teilerverhältnis v folgende
Werte:
v≤2
nmax = 2,7⋅ 10 20
(Suche nach großen Teilern)
1/3
14
v≤n
10
v≤n
2,0⋅ 10 9
Die Suche nach einem Teilerpaar (t1, t2) mit t2 ≤ 2t1 kann also bis oberhalb 10 20 vollständig
durchgeführt werden, während ein ’Primzahltest’ (v = n) nur bis 2⋅10 9 bereits 10 9 Schritte
beanspruchen würde.
Bevor im weiteren einige Möglichkeiten beschrieben werden, die geeignet sind, die
Effektivität des Verfahrens zu steigern, noch drei Anmerkungen:
a) Die Form x2 – y2 ist ein Sonderfall des allgemeinen Binoms xm – ym. Für dieses gilt:
x m − y m = ( x − y) ⋅
m −1
∑x
h
⋅ y m−1−h . Zur Gewinnung von Faktoren ganzer Zahlen ist nur der
h =0
(vorliegend behandelte) Fall m = 2 interessant, da – wie oben erwähnt – jede ungerade Zahl
eine solche Darstellung besitzt, während für m > 2 die Dichte dieser Zahlen immer weiter
zurückgeht und kein Kriterium bekannt ist, ob eine vorgegebene Zahl tatsächlich eine solche
Zerlegung besitzt.
[Aus der obigen Formel ist sofort ersichtlich, dass Zahlen, die als xm – ym (m > 1) darstellbar
sind, nur dann Primzahlen sein können, wenn x – y = 1 und es somit keine Primzahl der
Form n = xm – 1 geben kann, außer wenn x = 2 (Mersenne-Zahlen)].
b) Das hier behandelte Verfahren wurde zuerst von Pierre de Fermat (1601 – 1665)
beschrieben. Der Minoriten-Pater Marin Mersenne, über den vielfach der Kontakt Fermat’s zu
anderen Gelehrten Frankreichs lief, forderte Fermat in einem Brief auf, als Probe seines
Könnens die Faktoren der Zahl 100.895.598.169 anzugeben. Nach kurzer Zeit antwortete
Fermat: 112.303 und 898.423. Es ist allerdings kaum anzunehmen, dass er diese
bemerkenswerte Leistung mittels des nach ihm benannten o.a. Basis-Algorithmus geschafft
hat, denn damit findet man die Lösung erst nach rd. 190.000 Versuchen (, wenn die Suche ab
 n  sukzessive durchgeführt wird). Er hätte dann vermutlich keine Zeit mehr gefunden,
seinen berühmten ’letzten Satz’ aufzustellen.
Erstaunlich ist, dass Fermat trotz seiner Fähigkeiten im Faktorisieren die sog. 5. Fermat-Zahl
F5 = 232 + 1 für eine Primzahl hielt, obwohl 641 ein – zudem recht kleiner, zuerst von
L. Euler gefundener – Teiler von F5 ist.
c) Algorithmen werden hier größtenteils in leicht ‚lesbarem’ BASIC angegeben, wobei auf
Typdeklarationen, Speicherplatzzuweisungen u. dergl. ganz verzichtet wird und Ein-/
Ausgabe-Routinen nur schematisiert angedeutet werden.
5
2. Restklassen-Restriktionen
2.1 Unterscheidung nach den ungeraden Restklassen mod 4 und mod 8
Bei ungeradem n können in n = x2 – y2 die Variablen x und y nicht beide gerade oder beide
ungerade sein. Es sei zunächst x = 2v und y = 2w + 1; also n = 4v2 – (4w2 + 4w + 1) und
damit (n + 1)/4 = v2 – (w2 + w). Da die rechte Seite der Gleichung eine ganze Zahl ist, muss
es auch die linke sein, was gleichbedeutend ist mit n ≡ 3 mod 4.
Analog ergibt x = 2v + 1 und y = 2w : (n – 1)/4 = v2 + v – w2. Anstelle eine Lösung von
x2 – n = y2 zu suchen, tritt für
– (n + 1)/4 = w2 + w und
• n ≡ 3 mod 4: v2
• n ≡ 1 mod 4: v2 + v – (n – 1)/4 = w2
Wie eingangs beschrieben, ist die erforderliche Schrittzahl beim Fermat-Verfahren
proportional zur Wurzel n. Da hier n (annähernd) durch n / 4 ersetzt wird, kommt man mit der
halben Schrittzahl zum Ziel.
Mit diesem Ansatz und einer weiteren, unten erläuterten Überlegung, lässt sich das FermatVerfahren weiterentwickeln:
Eingabe: n (ungerade Zahl)
‘=====================================
‘Teil 1
IF n MOD 4 = 3 THEN b = (n+1)/4 ELSE b = (3*n+1)/4
u = INT (SQR(b)): m = u^2 – b
IF m = 0 THEN t1 = 2 * u – 1: t2 = t1 + 2: GOTO 11
w = 0: k = 1000
FOR i = 1 TO k
m = m + 2 * u + 1: u = u + 1
w = INT (SQR (m)): r = m – w *(w + 1)
IF r = 0 THEN
t1 = 2 *(u – w) – 1: t2 = 2 *(u + w) + 1: GOTO 11
END IF
NEXT i
'====================================
‘Synchronisation
w = w + 1: b = b + w^2 + w: h = 2 *(w + 1)
'====================================
‘Teil 2
q = INT (SQR(b)): g = 2 * q + 1: r = b – q^2
DO WHILE r > 0
DO WHILE r < g
r = r + h: h = h + 2
LOOP
r = r – g: g = g + 2
LOOP
t1 = g – h: t2 = g + h – 2
'====================================
11 IF n MOD 4 = 1 THEN
IF t1 MOD 3 = 0 THEN t1 = t1/3 ELSE t2 = t2/3
END IF
Ausgabe: Teiler: t1;t2
Das bedarf einiger Erklärungen:
– In Teil 1 sind die eingangs dieses Abschnitts gewonnenen Erkenntnisse verarbeitet.
Um den Programmcode nicht für die beiden Restklassen 1 und 3 (mod 4) trennen zu
müssen, werden Zahlen n ≡ 1 mod 4 mit 3 multipliziert; am Schluss wird die 3 dann
wieder aus dem Teilerpaar herausdividiert.
6
In der 3. Zeile wird der Sonderfall, dass b ein Quadrat ist, erledigt.
Wie man sieht, bereitet die Prüfung, ob die Zahl m von der Form w2 + w ist, keinerlei
zusätzliche Probleme; die üblicherweise benutzte (in dieser Basic-Version nicht
bereitgestellte) schnelle Funktion isqrt(x) kann auch in diesem Fall eingesetzt werden.
– Im oberen Teil wird – sofern nicht vorher eine Lösung gefunden wurde – eine
vorgegebene Anzahl (0 ≤ k < n) von Zyklen durchlaufen und die Ausführung dann an
Teil 2 (dritte Variante des Basis-Algorithmus gemäß Ziffer 1.) übergeben.
Funktionsweise: Eine Lösung ist gefunden, wenn in r = (n + 1)/4 + w2 + w – v2 der
Wert von r Null ist . Das ist gleichwertig zu f (w) –  f ( w )  = r wobei (n + 1)/4 +
w2 + w mit f (w) abgekürzt wurde. Die Differenz r der beiden Terme liegt stets im
Intervall [0, g] mit g = 2⋅  f ( w )  – 1; d.h. an den Sprungstellen infolge der
Rundung nimmt g jeweils um 2 zu. Bei rekursiver Darstellung dieser Zusammenhänge
folgt insgesamt daraus der o.a. Algorithmus.
2
Der eingangs dieser Ziffer 2.1 gemachte Ansatz lässt sich fortsetzen und führt zu folgendem
Ergebnis:
Bei den folgenden Restklassen mod 2 k existieren für alle Teilerpaare eines ungeraden n
natürliche Zahlen x und y, so dass im Fall ....
Restklasse
n ≡ 1(2) → n =
Teilerpaare
(x + y)⋅(x – y)
n ≡ 1(4) → n = (2x + 2y + 1)⋅(2x – 2y + 1)
n ≡ 3(4) → n = (2x + 2y + 1)⋅(2x – 2y – 1)
n ≡ 3(8) → n = (4x + 2y + 3)⋅(4x – 2y + 1)
n ≡ 7(8) → n = (4x + 2y + 1)⋅(4x – 2y – 1)
Berechnungsansatz →
Startwert für x
x2 – n = y2
n −1
= y2
x2 + x –
4
n +1
x2 –
= y2 + y
4
n−3
4x 2 + 4x –
= y2 + y
4
n +1
4x 2 –
= y2 + y
4
x=  n
x=

( n − 1) 
x=

n + 1
x=

n + 1
x=

1
2
1
2
1
4
1
4
( n + 1 − 2) 
Darüber hinaus scheint es keine derartigen Zerlegungen zu geben, die für eine gesamte
Restklasse mod 2 k Gültigkeit besitzen; vielmehr beschränkt sich deren Gültigkeit auf
bestimmte Teiler-Restklassen mod 2 k , was die Eignung zur Teilersuche naturgemäß
beeinträchtigt. Als Beispiel seien die beiden übrigen Restklassen mod 8 aufgeführt:
n ≡ 1(8)
– Restklassen der Teilerpaare mod 8 : (1, 1) und (5, 5)
n −1
n = (4x + 4y + 1)⋅(4x – 4y + 1)
2x 2 + x –
= 2y 2
8
– Restklassen der Teilerpaare mod 8 : (3, 3) und (7, 7)
n−9
n = (4x + 4y + 3)⋅(4x – 4y + 3)
2x 2 + 3x –
= 2y 2
8
7
n ≡ 5(8)
– Restklassen der Teilerpaare mod 8 : (3, 7)
4x 2 + 2x –
n = (4x + 2y + 3)⋅(4x – 2y – 1)
– Restklassen der Teilerpaare mod 8 : (1, 5)
4x 2 + 6x –
n = (4x + 2y + 5)⋅(4x – 2y +1)
n+3
= y 2 + 2y
4
n −5
= y 2 + 2y
4
Genauere Aussagen darüber, wie man im Fall des Modul 2 k zu den einzelnen Gleichungen
gelangt und wie man die Werte x und y bestimmt, sind im Anhang 1 aufgeführt. In der
folgenden Ziffer soll nun untersucht werden, wie im Falle eines allgemeinen Modul die
Lösungsmenge für x verringert werden kann. Es zeigt sich, dass dies in sehr effektiver Weise
möglich ist.
2.2 Verringerung der potentiellen Lösungsmenge
Für die (diophantische) Gleichung n = x2 – y2 werden ausschließlich ganzzahlige Lösungen
gesucht. Sie kann daher ohne weiteres als Restklassengleichung zu einem beliebigen Modul
m geschrieben werden: [n] = [x]2 – [y]2 (Wählt man m = n, ergibt das [0]n = [ x ]2n − [ y]2n , was
gleichbedeutend mit der sog. Legendre-Kongruenz x2 ≡ y2 mod n ist. Diese ist die Basis
nahezu aller heutigen leistungsfähigen Faktorisierungs-Verfahren.)
Im weiteren werden alle Restklassen durch ihre kleinsten nicht-negativen Vertreter
angegeben.
Anstelle n als Quadrate-Differenz darzustellen, lautet die Aufgabe jetzt, zunächst alle
’Quadrat-Reste’ r (man könnte auch sagen ’quadratische Reste’, für die aber wird
ggT(r,m) = 1 gefordert) ausfindig zu machen, deren Differenz eine prime Restklasse zum (frei
gewählten) Modul m ergibt. Besonders geeignet sind dabei natürlich Moduln, für die sich
diese Aufgabe mit möglichst wenigen Restklassen erfüllen lässt, denn nur die Werte von x,
die in die betr. Restklassen fallen, kommen für eine Lösung infrage.
Beispiel : m = 6
Restklassen: [0], [1], [2], [3], [4], [5]
Prime Restklassen: [1], [5]
Ermittlung der Quadrat-Reste:
a: 0, 1, 2, 3, 4, 5
a2: 0, 1, 4, 9, 16, 25
r = a2 mod 6: 0, 1, 4, 3, 4, 1
Die möglichen Quadrat-Reste sind also 0, 1, 3, 4. Mit diesen lassen sich für die beiden
primen Restklassen nur die folgenden Gleichungen [n] = [x]2 – [y]2 aufstellen:
[1] = [1] – [0]
[5] = [0] – [1]
[1] = [4] – [3]
[5] = [3] – [4]
Ersetzt man die Quadrat-Reste durch die zugrundeliegenden x- bzw. y-Werte/Restklassen,
erhält man alle in diesem Fall möglichen Restklassengleichungen:
[1] = [1]2 – [0]2
[5] = [3]2 – [2]2
2
2
[1] = [5] – [0]
[5] = [3]2 – [4]2
[1] = [2]2 – [3]2
[1] = [4]2 – [3]2
[5] = [0]2 – [1]2
[5] = [0]2 – [5]2
8
Dass für Zahlen n ≡ 1 mod 6 das gesuchte x insgesamt 4 der 6 Restklassen belegen kann
([1], [2], [4], [5]), lässt diese Vorgehensweise als nicht sehr effektiv erscheinen; bei
n ≡ 5 mod 6 sieht es mit nur zwei ’zulässigen’ Restklassen schon besser aus. Eine Halbierung
erzielt man durch Verwendung der eingangs gezeigten Tatsache, dass x bei Zahlen n ≡ 3 mod
4 stets gerade sein muss und im Fall n ≡ 1 mod 4 ungerade. Bei Verwendung eines geraden
Modul gilt das auch allgemein für die Restklassen von x.
Das abschließende Ergebnis für den Modul 6 lautet somit in Tabellenform:
n mod 6
1
5
x mod 6
n ≡ 1 mod 4 n ≡ 3 mod 4
1, 5
3
2, 4
0
Bei der praktischen Anwendung wird natürlich nicht jedes x darauf überprüft, ob es in einer
Restklasse liegt, die für eine Lösung infrage kommt, sondern zu jeder primen Restklasse von
n wird als Startwert für den Zyklus die kleinste Restklasse gespeichert und ausgehend von
dieser die Schrittfolge (Zyklus) festgelegt, bei deren Addition man immer auf einer zulässigen
Restklasse „landet“. Das sieht dann so aus:
n mod 6
1
5
x mod 6
n ≡ 1 mod 4
n ≡ 3 mod 4
Startwert Schrittfolge Startwert Schrittfolge
1
3
4, 2
6
2
0
2, 4
6
Für m = 2⋅3⋅5 = 30 erhält man folgende Tabelle:
n mod 30
1
7
11
13
17
19
23
29
n ≡ 1 mod 4
x mod 30
1, 5, 11, 19, 25, 29
1, 11, 19, 29
9, 15, 21
7, 13, 17, 23
9, 21
5, 7, 13, 17, 23, 25
3, 7
3, 15, 27
n ≡ 3 mod 4
4, 10, 14, 16, 20, 26
4, 14, 16, 26
0, 6, 24
2, 8, 22, 28
6, 24
2, 8, 10, 20, 22, 28
12, 18
0, 12, 18
9
2.3 Bestimmung optimaler Moduln (m und n sind teilerfremd)
Aus den beiden Beispielen (m = 6 und m = 30) ist ersichtlich, dass die Anzahl der xRestklassen (im Weiteren mit Ax bezeichnet) von der primen Restklasse n mod m abhängt.
In Anlage 1 ist dargelegt, dass
- Ax für Moduln m = p k (p > 2) nur zwei Werte annimmt (ϕ (m) / 2 – Ck (p) bzw.
ϕ (m) /2), je nach dem n mod p ein quadratischer Rest (QR) oder QNR ist.
- Ax für Moduln 2 e im wesentlichen davon abhängt, in welcher Restklasse zum Modul 8
n liegt.
- Ax sich für zusammengesetztes m sich durch Multiplikation aus den Ax-Werten der
Faktoren (Primzahlpotenzen) ergibt.
Mittels der Berechnung von Ax (ohne die x-Restklassen im Einzeln bestimmen zu müssen),
bietet sich eine einfache Möglichkeit, die Beschleunigung des Fermat-Verfahrens zu
beurteilen: Beim Basis-Alg. ist der mittlere Abstand der x-Werte gleich 1, da ab Wurzel n
jeder x-Wert überprüft wird, während der mittlere Abstand nun – durch Ausnutzen der
Tatsache, dass nicht jedes x die Kongruenz x 2 – n ≡ y 2 mod m zu lösen vermag – gleich
m / Ax ist.
Gemäß Anlage 1 ist für m = p k (p > 2) Ax ≤ 1 + ϕ (m) / 2, so dass der mittlere Abstand mit
jeden zusätzlichen Primteiler etwa um den Faktor 2 zunimmt; d.h. im Prinzip kann der
mittlere Abstand beliebig groß gemacht werden. Allerdings nimmt Ax mit jedem Primteiler
ungefähr um den Faktor p / 2 zu, was den Aufwand zur Berechnung der x-Restklassen stark
anwachsen lässt und dadurch der Vorteil der Abstands-Erhöhung überkompensiert werden
kann. Jedenfalls ist klar, dass m möglichst kleine Primfaktoren enthalten sollte.
Zur Festlegung der Exponenten der einzelnen Primfaktoren ist einerseits entscheidend, dass
wie erwähnt der Exponent k keinen Einfluss auf m / Ax hat, wenn n ein QNR zum Modul
p (p > 2) ist und –falls n ein QR ist – der Quotient m / (ϕ (m) / 2 – Ck) zügig gegen einen
Grenzwert Sg (p) konvergiert. (Z.B.: p = 2 → Sg = 24; p = 3 → Sg = 12; p = 5 → Sg = 4,3..;
p = 7 → Sg = 3.29..; usw.)
Die beiden folgenden Tabellen fassen die vorstehenden Aussagen zusammen:
m = 2e
e-opt.
S∅
n ≡ 1(8)
11
22,6
n ≡ 5(8)
5
8
m = pk
QR
p:
k-opt.
S∅
k-opt.
S∅
3
5
5
2
11,04 3,57
1
1
3
2,5
QNR
n ≡ 3(4)
3
4
← mittlerer Abstand = m / Ax
7
2
3,06
1
2,3
11
2
2,63
1
2,2
13
17
1
1
1,85 1,88
1
1
2,16 2,11
19
1
1,91
1
2,1 = 2p / (p – 1)
Beispiel: Aus Gründen des zur Verfügung stehenden Arbeitsspeichers sei m < 10 8.
- n sei QR nach 2, 3 und 5. Die Dimensionierung gemäß Tabelle ergibt: m = 2 11⋅3 5 ⋅5 2 ⋅7 =
87.091.200 → S∅ = 2.041 → Ax= 42.670. Ersetzt man 3 5 durch 3 4 → m = 29.030.400
→ S∅ = 1.878 → Ax= 15.458. Die Verringerung von Ax ist beträchtlich, während die
Verringerung des mittleren Abstands evtl. weniger ins Gewicht fällt.
- n sei kongruent 3 mod 4 und QNR nach 3 bis 19: m = 2 3 ⋅3⋅5⋅7⋅11⋅13⋅17⋅19 = 38.798.760
→
S∅ = 4⋅3⋅2,5 ⋅....⋅ 2,1 = 1.452 → Ax= 26.721.
10
Es stellt sich nun die Frage, wie die bisherigen Überlegungen in einen möglichst effizienten
Algorithmus umgesetzt werden können. Entscheidend ist dabei, dass die jeweils infrage
kommenden x-Restklassen mit wenig Aufwand gefunden werden. Die folgende Lösung (,die
nur für Zahlen kleiner 10 18 anwendbar ist,) macht von dem heute im PC allgemein eher
reichlich bemessenen Arbeitsspeicher umfänglich Gebrauch:
n=73445017 * 270985441
Teil 1: Optimaler Modul m
FOR i=1 TO 20: a(i)=q(i): NEXT i
q (i) = pi ( vorberechnete Primzahl-Folge)
IF n MOD 4=3 THEN a(1)=2^3
Festlegung des optimalen m (Ist n < 10 18
IF n MOD 8=5 THEN a(1)=2^5
sollten die Exponenten der Primfaktoren um 1
IF n MOD 8=1 THEN a(1)=2^10
reduziert werden (im Vergleich zu den ‘optimalen’)).
IF n MOD 3=1 THEN a(2)=3^4
g=n MOD 5: IF g=1 OR g=4 THEN a(3)=5^2
n ist QR mod p
g=n MOD 7: IF g=1 OR g=4 OR g=2 THEN a(4)=7^1
g=n MOD 11: IF g=1 OR g=4 OR g=9 OR g=3 OR g=5 THEN a(5)=11^1
m=1: FOR i=1 TO 12: m=m*a(i): IF m*a(i+1)>5*10^8 THEN i0=i: EXIT FOR
NEXT i: FOR i=1 TO i0:PRINT a(i): NEXT: PRINT , “ m = “;m
‘-------------------------------------------------------------- Teil 2:
FOR i=0 TO m-1: r =(i^2)MOD m: u(r)=1:NEXT i
Speichern aller QR (= y 2) als Adresse in u ( )
s=n MOD m: k=0
FOR x=0 TO m-1
Speichern aller möglichen Lösungen x von
r=(x^2)MOD m-s: IF r<0 THEN r=r+m
x 2 – n ≡ y 2 mod m als Adresse in p ( )
IF u(r)=1 THEN k=k+1: p(x)=1
NEXT x: ax=k
ax = Ax
FOR i=0 TO m-1: IF p(i)=1 THEN EXIT FOR
d (- 1): Startwert der
NEXT i: d(-1)=i: a=i: k=-1
Differenzen-Folge (Fixpunkt)
FOR i=a+1 TO m-1:IF p(i)=1 THEN k=k+1:d(k)=i-a: a=i
Berechnen der Differenzenfolge aus
NEXT i: d(k+1)=2*d(-1)
den x-Werten und Speichern in d ( )
'-------------------------------------------------------------Teil 3:
u0=INT(SQR(n)): ru=u0 MOD m: i=0: uw=d(-1)
Da die Lösungssuche im Fermat-Verfahren
FOR i=0 TO ax: uw=uw+d(i)
bei Wurzel n beginnt, ist zunächst der
IF uw+d(i+1)=>ru THEN EXIT FOR
passende Startwert modulo m in der Diff.NEXT i: u=u0-ru+uw: w=0: v=1: k=0
Folge zu suchen (u = u0 – u0 mod m + uw).
‚-------------------------------------------------------------DO WHILE v<>w^2
Hauptteil
k=k+1: i=i+1: IF i=ax THEN i=0
‘Zyklenschalter’ für die Differenzenfolge
u=u+d(i): v=u^2-n: w=INT(SQR(v))
Anstelle u = u + 1 nun u = u + d (i)
LOOP
PRINT n, u+w; u-w, (u+w)*(u-w)
Ergebnis (Teilerpaar von n)
PRINT ax, m/ax, k
Ax, mittl. Abstand, Anzahl Schritte bis zur Lösung
Für die angenommene Beispiel-Zahl erhält man: m = 107.627.520, Ax = 55.296, S∅ = 1.946
Die Do while..Loop-Schleife wird 828.272-mal durchlaufen; im Basis-Alg. wären rd.
1,6 ⋅10 9 Durchläufe erforderlich.
Fazit: Durch Vergrößerung des Moduls m (Erhöhung der Anzahl der Primfaktoren) lässt sich
der mittlere Abstand prinzipiell beliebig vergrößern. Da die potentielle Lösungsmenge für
Primfaktoren p > 20 in etwa proportional zu p ist, während sich der Abstand nur etwa
verdoppelt, erhöht sich der Aufwand zur Berechnung der Ax x-Restklassen letztlich so stark,
dass der Zeitaufwand der Vorausberechnungen die Ersparnis bei der finalen Quadratsuche
übersteigt.
Eine Implementierung gemäß dem obigen Basic-Code (schnell, aber mindestens 4 GB
Arbeitsspeicher erforderlich; Begrenzung des Modul auf 5⋅10 8 ) liefert mittl. Abstände von
11
bis zu 3000 (bei Ax-Werten < 10 5) , was insgesamt eine Erweiterung des Einsatzbereiches des
Fermat-Verfahrens um den Faktor 10 7 (bei gleichem Zeitaufwand) ermöglicht !
Anmerkungen:
• Ein Grund dafür, dass man in den einschlägigen Darstellungen kaum Hinweise auf
oben beschriebene Optimierungs-Möglichkeit findet, dürfte sein, dass weitere
Verbesserungen sehr naheliegend sind; aber das firmiert dann nicht mehr unter
„Fermat-Verfahren“.
•
Der obige Algorithmus bezieht sich auf die Zerlegung n = x2 – y2. Das Verfahren
lässt sich (mit einem leicht modifizierten Algorithmus) aber auch auf die für
Zahlen n ≡ 3 mod 4 mögliche und um den Faktor zwei schnellere Zerlegung
v2 – (n + 1)/4 = w2 + w anwenden. Unterscheidet man dann danach, ob (n + 1)/4
gerade oder ungerade ist, entstehen genau die gleichen Schrittfolgen-Zyklen, wie
bei der Zerlegung n = x2 – y2 und Auftrennung in die beiden ungeraden
Restklassen mod 4; allerdings ist die Zuordnung zu den jeweiligen primen
Restklassen eine andere. (Für Zahlen n ≡ 1 mod 4 funktioniert die letztere
Aufteilung nicht.)
•
Der Algorithmus kann unverändert auf gerade Zahlen (n ≡ 0 mod 4) angewandt
werden (wobei der Modul dann natürlich ungerade sein muss).
•
Zu Vervollständigung noch ein weitere, manchmal beschriebene Variante:
Ist n ungerade, sind es auch Teiler und Komplementärteiler jeden Teilerpaares:
n = t1⋅t2 = (2ks + 1)(2ls + 1). Daraus: n + 1 = 4kls2 + t1 + t2 und schließlich
t1 + t 2
n+ 1
2
2 ≡ 2 mod ( 2s ) . Andererseits ist immer noch
t +t
n = t1⋅t2 = ( 1 2 2 ) 2 − ( t1 −2 t 2 ) 2 = x2 – y2 . Folglich kommen für x nur die Werte
infrage, die in der gleichen Restklasse ( mod 2s2) liegen, wie (n+1)/2. Liegen (wie
das meistens der Fall ist) keine Informationen über die Struktur der Teiler vor,
bleibt nur s = 1; d.h. x liegt in der Folge der geraden bzw. ungeraden Zahlen. Aber
bei den Mersenne-Zahlen ist
x ≡ 22p–1 mod (2p2) und
p
bei den Fermat-Zahlen ist
x ≡ ( 2 2 −1 + 1) mod (22p+1) .
•
In jedem Zyklus des Fermat-Verfahrens ist zu prüfen, ob eine Zahl m = u2 – n eine
Quadratzahl ist, was einen Großteil der gesamten Rechenzeit beansprucht. Auch die
Anzahl dieser Prüfungen lässt sich aufgrund von Restklassen-Restriktionen wesentlich
einschränken: Sei q ein Quadrat und r die Restklasse von q zu einem Modul h. Dann
ist [s] = [r]2 die Restklasse von q. s ist also Quadrat-Rest und die Quadrat-Reste stellen
für h > 2 immer nur eine Teilmenge der Restklassen {0,1,.......,h–1} dar.
Kleinstes Beispiel: h = 3
[r]
[r]2
0
0
1
1
Folglich ist eine Zahl n ≡ 2 mod 3 kein Quadrat.
2
1
Bei einem im Sinne der hier gestellten Aufgabe zweckmäßigen Modul sollte der
Quotient h / k groß sein, wobei k die Anzahl der Quadrat-Reste bezeichnet. Je größer
nämlich dieser Quotient ist, mit desto größerer Wahrscheinlichkeit werden Nicht12
Quadrate „herausgefiltert“. Beim Modul 10.080 ist h / k = 30; d.h. knapp 97% aller
Nicht-Quadrate werden als solche erkannt! Diese Quote lässt sich mit wesentlich
größeren Moduln natürlich noch übertreffen, aber die Rechenzeit beeinflusst das kaum
noch.
Die Umsetzung dieses „Quadrat-Filters“ in einen Algorithmus kann folgendermaßen
aussehen:
Mat a() = Zer: h = 10080
For i = 0 to h –1: q = i^2 mod h: a(q) = 1: Next i ((Abspeichern der QuadratEingabe: n
Reste im Vektor a(). ))
u0 = isqrt(n): m = u0^2 – n
For u = u0 + 1 to n
m=m+u+u+1
s = m mod h: If a(s) <>1 then Iterate (***)
w = isqrt (m): If w^2 = m then Exit For
Next u
Ausgabe: Teilerpaar (u – w); (u + w)
Durch Einfügen der mit (***) gekennzeichneten Programm-Zeile wird eine
Verkürzung der Rechenzeit um etwa 30% erzielt (, wobei die Verkürzung mit der
Größe von n leicht zunimmt).
13
3. Beaufschlagung der zu zerlegenden Zahl mit Faktoren
3.1 Beschreibung der Wirkungsweise
Wie in Abschnitt 1. gezeigt, arbeitet das Fermat-Verfahren am besten, wenn Teiler und
Komplementärteiler einer Zahl nahe bei n liegen, also das Teilerverhältnis v (= t2/t1 mit
t2 > t1) nicht viel größer als 1 ist. Im weiteren werden nun Möglichkeiten untersucht, die
vorgelegte Zahl n mittels Faktoren f derart zu „manipulieren“, dass das Teilerverhältnis v´
eines Teilerpaares von f⋅n kleiner als v ist. Findet man ein Teilerpaar von f⋅n, so können die
(gesuchten) Teiler von n leicht per ggT-Berechnung bestimmt werden.
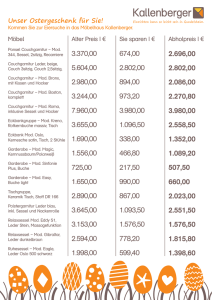
Zunächst soll die Auswirkung eines Vorfaktors anhand der folgenden Grafik veranschaulicht
werden.
20000
i (Schrittzahl)
16000
n = pi⋅pj ≈ 108 (pi, pj prim)
v = pi / pj (pi > pj)
12000
19,46
f=1
8000
5,0
5,94
f = 16
4000
2,0
7,7
f = 15
15
4,0
0
11 1,66
6
11
16
21
v
Bild 1: Auswirkung auf die zum Auffinden eines Teilers von n erforderliche Schrittzahl i in
Abhängigkeit vom Teilerverhältnis v am Beispiel der Vorfaktoren 15 und 16 im Vergleich
zum Basisalgorithmus (f = 1). (Es wurden nur Zahlen pi ⋅pj zerlegt, deren Produkt möglichst
nahe bei 108 liegt, um die Auswirkung von n auf die Schrittzahl (s. 1. ∗∗) zu neutralisieren.)
Dem Bild entnimmt man, dass der Vorfaktor 15 ab v = 5,94 eine erhebliche und nachhaltigere
Verringerung der Schrittzahl, die zum Auffinden eines Teilers von n benötigt wird, bewirkt,
während dies bei f = 16 nur (und in wesentlich kleinerem Ausmaß) im Bereich
2,51 < v < 19,46 der Fall ist.
14
Da das Teilerverhältnis bei einer vorgelegten Zahl nicht bekannt ist, sondern gerade die
gesuchte Größe ist, sind Vorfaktoren nur sinnvoll anzuwenden (sie können ja auch eine
Vergrößerung der Schrittzahl zur Folge haben), wenn klar ist, wie die im Bild beispielhaft
dargestellten Kurven zustande kommen.
Sei f eine Zahl mit r Teilerpaaren f = hk⋅tk , für die t k ≡ h k mod 2 gilt. Mit der Festlegung
h
h k ≥ t k und 1 < h k < h k + 1 ≤ f ist dann 1 ≤ ..< ht kk < t kk ++11 < ...≤ f. (Den Wert 1 kann der
Quotient nur annehmen, wenn f eine Quadratzahl ist; den Wert f – wegen t k ≡ h k mod 2 – nur,
wenn f ungerade ist.)
Im weiteren werden die Quotienten hk / tk mit vk bezeichnet.
Beispiele:
f = 15 → v1 = 5 / 3; v2 = 15 / 1
f = 16 → v1 = 4 / 4; v2 = 8 / 2
f = 3⋅5⋅7 → v1 = 15 / 7; v2 = 21 / 5; v3 = 35 / 3; v4 = 105 / 1
Gemäß Ziffer 1. (Seite 2) besteht beim Basisalgorithmus zwischen der Schrittzahl i und dem



( v − 1)

Teilerverhältnis v der formelmäßige Zusammenhang i = 
bzw. ( bei
 2 ⋅ v  ⋅ n  +1



Vernachlässigung der 1 sowie der Rundung) i = (
v
1
+
1
v
2
− 2)⋅
n
2
. Diese Formel gilt
natürlich auch, wenn n durch f⋅n ersetzt wird. Bezogen auf die Teiler von n ist das
gleichbedeutend mit i =
(
v
vk
+
vk
v
− 2)⋅
f⋅ n
2
(3.∗)
wobei vk der Reihe nach die Werte von v1 bis vr durchläuft. Dabei erfolgt der Übergang von
vk auf vk + 1 genau dann, wenn für einen eindeutig bestimmten Wert von v (= vs) gilt:
i (vs, vk) = i (vs, vk + 1).
Mit (3.∗) kann der Verlauf von i(v) leicht beschrieben werden:
Für v = vk ist der Klammerausdruck gleich Null, d.h. i(v) besitzt r Minima mit i(v = vk) = 0.
Der Schnittpunkt der beiden Kurven i(v, vk) und i(v, vk + 1) liegt bei v = vs, k =
v k ⋅ v k +1 .
Dieser Punkt ist jeweils ein rel. Maximum im Verlauf i(v).
Beispiele:
f = 15: vs, 1 = (5 / 3) ⋅ (15 / 1) = 5
Siehe Bild 1
f = 16: vs, 1 =
( 4 / 4) ⋅ (8 / 2) = 2
f = 105: vs, 1 = (15 / 7) ⋅ ( 21 / 5) = 3, vs, 2 = 7, vs, 3 = 35
Etwas schwieriger und auch rechenintensiver ist die Bestimmung der Schnittpunkte von
Verläufen zweier unterschiedlicher Vorfaktoren (f1 und f2). Die Gleichsetzung der beiden für
f1 bzw. f2 gültigen Terme (3.∗) führt auf eine quadratische Gleichung mit den beiden
Lösungen
va,b = (
− e ± e 2 − 4⋅u⋅w 2
) . (3.∗∗) Darin sind
2⋅u
e = 2 v k ⋅ v m ( f1 − f 2 )
u=
v k ⋅ f 2 − v m ⋅ f1
w=–
v k ⋅ v m ( v k ⋅ f1 − v m ⋅ f 2 )
Der Quotient des m-ten Teilerpaares von f2 ist zur Unterscheidung mit vm bezeichnet,
während vk (wie oben eingeführt) der Quotient des k-ten Teilerpaare von f1 ist.
15
Die so ermittelten Lösungen geben nur dann die gesuchten Ordinaten der Schnittpunkte
wieder, wenn zwischen v = vm und v = vk keine weiteren „Nullstellen“ der betrachteten
Vorfaktoren liegen. Im Beispiel f = 15 und f = 16 aus Bild 1 gibt es für die ’v-Paare’
(15/1, 8/2), (5/3, 8/2) sowie (5/3, 4/4) jeweils nur einen Schnittpunkt (v = 7,7..; 2,59..und
1,285..), der zwangsläufig zwischen den betreffenden zwei Nullstellen liegt. (In den drei
Fällen ist die zweite Lösung von (3.∗∗) kleiner Eins und somit nicht von Interesse.)
Zu beachten ist noch der Sonderfall v k = o 1 / e und v m = o 2 / e – wenn also die beiden
Nenner gleich sind (z.B. f1 = 4 →vk = 2 / 2 und f2 = 16 → vm = 8 / 2 ). Dann existiert nur ein
Schnittpunkt, und der besitzt die Ordinate vs =
(
o 2 − o1
2 ⋅( f 2 − f 1 )
).
2
Nach soviel „Kurvendiskussion“ soll nun die Nutzung von Vorfaktoren in konkreten
Algorithmen geprüft werden.
3.2 Beaufschlagung von n mit einem festen Vorfaktor
Nimmt man an, dass bei einem vorgegebenen n = t1⋅t2 das Teilerverhältnis v = t1/t2 für alle
möglichen Werte von v unterhalb einer bestimmten Grenze vo gleich wahrscheinlich ist (d.h.
v ist statistisch gleichverteilt), kann man den Vorteil (Nachteil), der sich im Mittel bei
Anwendung eines bestimmten Vorfaktors einstellt, leicht berechnen indem die Fläche
unterhalb der Kurve i = f(v)|v = v1 zu der entsprechenden Fläche für i = f(v)|v = v2 ins Verhältnis
gesetzt wird.
Weil es nicht auf die absoluten Flächengrößen ankommt, sondern nur auf deren Verhältnis,
kann man immer auf i / n normieren, d.h. die Ergebnisse sind von n unabhängig.
1
−1
Besonders einfach ist die Berechnung im Fall f = 1: Wegen in = 12 ( v 2 + v 2 − 2 ) gilt
v0
Ff = 1 =
1
2
−
∫ ( v + v − 2 ) dv = 13 ⋅ ( v o − 1) + ( v o − 1) − ( v o − 1) .
1
1
2
3
2
1
2
2
1
Besitzt f mehrere (k) Teilerpaare mit den nach aufsteigender Größe geordneten
Teilerverhältnissen vi , sind als erstes daraus – wie oben gezeigt – alle Schnittpunkte vs,i < vo
zu berechnen. Die zwischen den Schnittpunkten vs, i – 1 und vs, i liegenden Kurvenzüge können
jeweils analog zum Fall f = 1 integriert werden. Die gesuchte Gesamtfläche Ff ist dann die
Summe der m Einzelflächen:
m
Ff =
∑ Ff , i = ∑
i =1
vs , i
m
i =1
f
2
∫ (
v s , i −1
v
vi
+
vi
v
− 2) dv Es ist vs, 0 = 1 und vs, m = vo zu nehmen. Die i-te
3
3
1
1
Einzelfläche ergibt sich zu Ff, i = f ⋅  3⋅ 1v ( v s,2i − v s ,2i −1 ) + v i ( v s ,2i − v s,2i −1 ) − ( v s , i − v s , i −1 )
 i

In der nachstehenden (auch experimentell verifizierten) Tabelle sind für einige vo und
Vorfaktoren f die Quotienten der im Mittel erforderlichen Schrittzahlen if = 1/if =fo
angegeben. (Der Eintrag 3,44 bedeutet also, dass die erforderliche Schrittzahl bei
Verwendung des Vorfaktor f sich im Vergleich zum Basisalgorithmus (f = 1) um den Faktor
3,44 verringert.) Die markierten Werte stellen die Optima einer Vielzahl getesteter
Vorfaktoren dar.
f \ vo:
5
10
100
1000
1.440
2.880
10.080
181.440
Tabelle 3.1
3,44 (5)
2,10 (5)
2,00 (8)
0,81 (13)
4,41
6,25
3,95
2,39
14,41
18,12
23,74
10,60
16
6,13 (In Klammern
14,22 gesetzte Zahlen:
14,27 Siehe Text unten)
32,69
Die Aussagen der Tabelle sind insofern zu relativieren, als die Annahme, die v-Werte seien
unterhalb der Grenze vo gleichverteilt, bekanntlich nicht zutrifft. Z.B. besitzen rd. ein Drittel
aller ungeraden 7-stelligen Zahlen (ohne Primzahlen und Quadratzahlen) mindestens ein
Teilerpaar (t1, t2) mit t2 / t1 < 5, d.h. die restlichen zwei Drittel verteilen sich auf den Bereich
5 bis 107 / 3. Bei rd. 11 % der genannten Zahlen ist sogar t2 / t1 < 1,5 (jeweils t2 > t1).
Daraus ist zu folgern, dass nur die drei erstgenannten Vorfaktoren in Frage kommen; diese
aber „im Mittel“ einen erheblichen Vorteil bringen. Die wesentliche Aussage der Tabelle ist
aber, dass – wie auch immer vo gewählt wird – es für den Vorfaktor einen optimalen Wert
gibt, und eine weitere Vergrößerung die erforderliche Schrittzahl erhöht, auch wenn der betr.
Faktor u.U. sehr viele „Nullstellen“ im Bereich 1 bis vo aufzuweisen hat (siehe Zahlen in
Klammern unter vo = 5).
Ein weiterer Aspekt, unter dem ein Vorfaktor bewertet werden kann (und der auch weiter
unten Anwendung findet), ist seine „effektive Schrittlänge“ (des ersten Schritts).
Dazu ist (3.∗) nach
v aufzulösen:
v=
(
v k 1+
i
f ⋅n
± (1 +
i
f ⋅n
)
) 2 −1 .
(3.∗∗∗)
 n + i ⋅( 1 ± 1 + 2⋅ f ⋅ n )  umformen. Für (rel.) kleine Werte


i
f


von i ist die 1 unter dem Wurzelzeichen vernachlässigbar, was zu der leichter
interpretierbaren Darstellung
v
2⋅ v
v = 1n  v k n + i⋅ fk ± i⋅ 4 f k ⋅ 4 n  führt.


Bei Verwendung eines Vorfaktors werden die Umgebungen aller „Nullstellen“ v = v k im
ersten Schritt simultan darauf getestet, ob sich eine Quadratdarstellung und somit ein Teiler
von n findet. Die beiden Grenzwerte für das Teilerverhältnis der k-ten „Nullstelle, bei der ein
Teiler im 1. Schritt gefunden wird, sind diejenigen Werte, für die der in den
Das lässt sich zu
v=
vk
n

Rundungsklammern stehenden Term der Beziehung i = (
gleich 1 ist. In der obigen Auflösung nach
v⋅ n=
t2
t1
v
vk
+
vk
v
− 2) ⋅
f⋅ n
2
 + 1 gerade
v ist also i = 1 einzusetzen und wegen
⋅ t 1 ⋅t 2 = t2 erhält man schließlich das Intervall, in dem der Teiler t2 im ersten
Schritt gefunden wird: ∆ t2 =
2⋅ 2 ⋅ v k
4f
⋅ 4 n (= d ⋅
4
n ).
Somit hat man in dem vor der 4-ten Wurzel n stehenden Faktor d einen Bewertungsmaßstab
für verschiedene Vorfaktoren, wobei für einen vorgegebenen Vorfaktor f und ein
vorgegebenes vo die Summe über die vk zu bilden ist, die kleiner als vo sind.
Ist vk =1, was nur bei Vorfaktoren vorkommt, die Quadratzahlen sind, ist die Besonderheit zu
beachten, dass in dem Ausdruck für d anstelle der 2 eine 1 zu setzen ist, da v hier immer
größer 1 definiert ist (t2 > t1; z.B. f =1: d = 1⋅ 2 ).
In der nachstehenden Tabelle sind die effektiven Längen des ersten Schritts (Vielfache von
4
n ) für einige Vorfaktoren aufgelistet.
17
f \ vo:
5
1
3
4
16
1440
2880
10080
20160
60480
1,41
3,72
1,0
3,53
3,63
3,72
3,37
3,58
3,32
Summe di für v < vo
10
100
6,15
5,91
5,54
5,45
5,77
17,35
17,05
17,83
18,48
18,15
1000
alle
26,06
32,59
36,00
36,90
44,29
50,18
62,17
84,95
Tabelle 3.2: Effektive Länge des ersten Schrittes bezogen auf 4 n für
ausgewählte Vorfaktoren. Die insgesamt gefundenen Maximalwerte sind markiert.
Ein Vergleich mit Tabelle 3.1 zeigt, dass die Lage der Optima recht gut
übereinstimmt.
3.3 Der serielle Einsatz von Vorfaktoren
Naheliegend ist der Gedanke, der Reihe nach Vorfaktoren mit den „Nullstellen“ 1, 2, 3, 4,
5,.... anzuwenden, indem jeweils die Schnittpunkte (vf, if) für aufeinander folgende
Vorfaktoren berechnet werden und sodann der Basisalgorithmus mit if Schritten für die Zahl
f⋅n ausgeführt wird. Für große n ergeben sich mit diesem Verfahren allerdings leicht zu große
Werte von if . Um hier mehr Flexibilität zu erhalten, kann man wie folgt vorgehen:
Vorab wird die max. Schrittzahl imax , mit der ein Vorfaktor höchstens eingesetzt wird, sowie
das max. Teilerverhältnis vmax , für das ein Teilerpaar von n gesucht wird (z.B. vmax = 3),
festgelegt. (Die Begrenzung auf vmax ist kein Nachteil, da die sukzessiv eingesetzten
Vorfaktoren auch (in der Regel zahlreiche) „Nullstellen“ besitzen, die größer als vmax sind
und die Umgebung dieser Nullstellen jeweils simultan auf Teiler getestet wird. Wird dennoch
ein Teilerpaar mit v > vmax nicht gefunden, kann das Verfahren anschließend für die Zahl
n⋅vmax wiederholt werden.)
Als erstes werden die ‚Ränder’ des v–Bereichs mit f = 1 bzw. f = vmax bearbeitet. Durch
Einsetzen von imax in (3.∗∗∗) und quadrieren erhält man u. a. die beiden Werte v1,o und vmax,u;
diese werden abgespeichert. Der zwischen diesen beiden Eckpunkten liegende Bereich wird
nun mittels weiterer Vorfaktoren fx solange mit Intervallen [vx,u – vx,o] aufgefüllt, bis der
gesamte Bereich belegt ist.
Dabei wird die Folge der Vorfaktoren f = c⋅s (v = c / s) wie folgt gebildet:
Der Nenner s durchläuft – beginnend mit s = 2 – die Folge der (ersten) natürlichen Zahlen.
Zu jedem Wert von s durchläuft der Zähler c (mit Schrittweite 2) alle Werte von c = s + 2 bis
c = vmax⋅s – 2.
18
Die ersten f-Werte z.B. für vmax = 3 sind demnach:
s
2
3
4
5
6
7
f = c⋅s
4⋅2
5⋅3
7⋅3
8⋅4
6⋅4
7⋅5
9⋅5
8⋅6
10⋅6
...... ......
10⋅4
11⋅5
12⋅6
13⋅5
14⋅6
16⋅6
Treten dabei die Fälle ggT(c, s) > 2 (in der Tabelle rot) oder c ≡ 2 mod 4 und zugleich
s ≡ 2 mod 4 (in der Tabelle blau) auf, wird der betr. Vorfaktor f = c⋅s übergangen (, da die
gekürzten Brüche zuvor bereits zur Anwendung kamen). Insgesamt stellt dieses Vorgehen
sicher, dass betragsmäßig kleine Vorfaktoren bevorzugt zur Anwendung kommen.
Für jeden ‚brauchbaren’ Vorfaktor fx werden mit i = imax die beiden Grenzen vx, o und vx, u
berechnet. Dabei sind – um Überschneidungen und damit Doppelarbeit zu vermeiden –
folgende Fälle zu beachten:
1. Die „Nullstelle“ c / s des aktuellen Vorfaktors fx fällt in einen Bereich, der bereits
von einem der vorhergehenden Vorfaktoren ‚belegt’ ist → fx wird übergangen.
2. a) vx,o liegt in einem bereits durch irgendeinen Vorfaktor fy belegten Bereich (d.h.
vx,o > vy,u; siehe Bild 2). Dann ist durch Einsetzen von vy,u in (3.∗∗) die
(abzuspeichernde) Schrittzahl ix,o < imax und mit dieser wiederum das verkleinerte
vx,u zu berechnen. (Damit schließt der von fx belegte Bereich exakt an den Bereich
von fy an.)
i
belegt
Lücke
belegt
imax
fx
x
RestLücke
fz
vz, o
fy
ix, o
vx, u
vx, o = vy, u
v
Bild 2
b) vx,u liegt in einem bereits durch irgendeinen Vorfaktor fz belegten Bereich (d.h.
vx,u < vz,o). → Analog zu a).
c) vx,o und vx,u liegen beide in (von zwei verschiedenen Vorfaktoren) bereits belegten
Bereichen (siehe Bild 3). Mit Hilfe von vz,o und vy,u werden ix,u und ix,o berechnet;
der größere der beiden i-Werte (im Bild ix,u) ist abzuspeichern. Damit ist der v19
Bereich zwischen fz und fy belegt, (wobei eine geringfügige Überlappung (im Bild
ist vx,o > vy,u) in Kauf genommen wird).
i
belegt
Lücke
belegt
imax
x
ix,u
fz
fx
fy
ix,o
vx,u = vz,o
vy,u
v
Bild 3
Auf diesem Wege lassen sich die zur vollständigen Belegung des vorgegebenen v-Bereiches
erforderlichen Vorfaktoren (unter Berücksichtigung der je Vorfaktor maximalen Schrittzahl)
bestimmen. Zur schnellen und einfachen Umsetzung für die praktische Nutzung sind
allerdings noch zwei Punkte zu berücksichtigen:
– Die strikte Vorgabe von imax kann dazu führen, dass zwischen zwei belegten Bereichen
eine sehr kleine Lücke bestehen bleibt und es schwierig ist, für diese einen geeigneten
Vorfaktor zu finden. Das kann man vermeiden, indem jeweils geprüft wird, ob die
verbleibende Lücke durch eine geringe Überschreitung von imax ( z.B. < 5% )
vollständig geschlossen werden kann. Falls ja, wird für den betr. Vorfaktor imax soweit
wie erforderlich erhöht (Überführung von Fall 2.a) in 2.c)).
– Wie gesagt, ist für jeden Vorfaktor fx zu überprüfen, inwieweit der Bereich [vx,u – vx,o]
noch frei ist. Um langwierige Suchvorgänge zu vermeiden, ist es zweckmäßig die von
den betreffenden Vorfaktoren belegten Bereiche ‚geordnet’ abzuspeichern. Eine leicht
umzusetzende Möglichkeit besteht darin, die Werte vx,u und vx,o mit Faktor B (nat.
Zahl) zu multiplizieren und B⋅vx,u sowie B⋅vx,o (nach Abrundung) in einem Vektor der
Länge B⋅vmax abzulegen. Der gesamte Bereich zwischen Bvx,u und Bvx,o wird als
‚belegt’ markiert.
Zur Überprüfung der quantitativen Wirksamkeit des beschriebenen Konzeptes wurde das im
Anhang 2 beigefügte Programm benutzt. Es ergaben sich z.B. folgende Verminderungen der
erforderlichen Schrittzahl im Vergleich zum Basis-Alg.(vmax = 3 und unter der Annahme, dass
das Teilerverhältnis der Faktoren von n in der Nähe von vmax liegt):
n ≈ 10 16 , imax = 200 → Schrittzahlverringerung um den Faktor 110
n ≈ 10 29 , imax = 10 7 → Schrittzahlverringerung um den Faktor 380
Da der Zeitaufwand zur Durchführung des Programms praktisch vernachlässigbar ist, ist die
Laufzeitverringerung in der Größenordnung der Schrittzahlverringerung. Allerdings lohnt der
Einsatz sich – wegen des kleinen vmax – sich erst für n > 1020.
20
Fazit: Kombiniert man den seriellen Einsatz von Vorfaktoren mit dem Verfahren zur
Schrittlängenvergrößerung gemäß Ziffer 2. lassen sich große Teiler (vmax < 5) von Zahlen bis
etwa 1030 bestimmen; eine Größenordnung, die üblicherweise nicht mit dem FermatVerfahren in Zusammenhang gebracht wird.
21
4. Das Lehman-Verfahren
4.1 Der Basis-Algorithmus
Die konsequente Weiterführung der in Ziffer 3. diskutierten Verwendung von Vorfaktoren
führt auf das nachstehende, von Lehman entwickelte Verfahren, dessen Zeitbedarf
proportional zur dritten Wurzel von n ist.
Eine vorgelegte Zahl n` wird zunächst per Probedivision darauf überprüft, ob ein (oder
mehrere) Teiler t <= n`1/3 vorhanden sind; diese werden ggf. herausdividiert. Die verbleibende
Zahl n ist somit entweder prim oder – da n keine drei Faktoren enthalten kann, die alle größer
n1/3 sind – von der Form n = pi⋅pj (pi, pj prim; pi < pj) mit pi > n1/3 und pj < pi2.
Unter Beachtung dieser Voraussetzungen sieht der (Standard-)Algorithmus des LehmanVerfahrens wie folgt aus:
Eingabe: n
(Der kleinste Primteiler von n muss größer n1/3 sein; s.o.)
For f = 1 To n^(1/3)
fn = 4*f*n: ug = Int(Sqr(fn)) + 1: og = ug + Int(n^(1/6)/(4*Sqr(f)))
For u = ug To og
m = u^2 – fn: w = Int(Sqr(m))
If m = w^2 then Exit, Exit
Next u
Next f
Ausgabe: Teiler: t1 = ggT(u + w, n), t2 = n / t1
f durchläuft ggf. alle Zahlen von 1 bis 3 n . U.A. um auch die Werte von f verwenden zu
können, für die f ≡ 2 mod 4 ist, wird n generell vorab mit 4 multipliziert. Zu den Einzelheiten,
insbesondere zum Beweis, dass unter den genannten Voraussetzungen immer ein Teiler
gefunden wird, sei auf diesbezügliche Darstellungen im Netz verwiesen .
Nachteilig zu werten ist, dass die „Ordnung“ insofern verloren geht, als Teiler, die z.B. ganz
in der Nähe von 2 n liegen, dennoch u. U. erst nach relativ vielen Schritten gefunden werden.
Daher eignet es sich nicht zur gezielten Suche nach großen Teilern von Zahlen.
4.2 Optimierungen des Lehman-Verfahren
Als erstes liegt eine Aufteilung des Algorithmus nahe, denn die ’u-Schleife’ wird nur solange
benötigt, wie n1/6 / (4⋅ f ) > 1. Also ist die Berechnung der oberen Grenze der u-Schleife nur
bis f = n1/3 /16 erforderlich.
Des Weiteren: Wendet man den „Multiplikator“ 4 nur auf die geraden Werte von f an,
resultiert daraus im Mittel eine Verkürzung der Rechenzeit um etwa 15 %; bei ungeradem f ist
die Multiplikation mit 4 überflüssig und nachteilig. (Die Bezeichnung „Multiplikator“ wird
benutzt zwecks Unterscheidung vom „Vorfaktor“ 4⋅f .)
Es stellt sich außerdem die Frage, ob die 4 als Multiplikator optimal ist. Wie sich zeigt , ist die
16 deutlich effektiver. Im Mittel ergibt sich nahezu eine Halbierung der Rechenzeit, was man
mit Hilfe des im Anhang 3 beigefügten Programms verifizieren kann. Das liegt zum einen
daran, dass der Multiplikator 16 zusätzlich zu vk = 4 / 4 = 1 noch über die „Nullstelle“
vk = 8 / 2 = 4 verfügt (siehe Bild 3.1) und die Anzahl Durchläufe der inneren Schleife sich um
rd. ¾ reduziert.
22
4.3 Der „Spitzendetektor“
Es scheint allerdings so zu sein, dass die Multiplikatoren 4 und 16 die einzigen sind, die für
alle dem Lehman-Verfahren zugänglichen Zahlen die Forderung erfüllen, dass ein Teiler von
n spätestens nach n1/3 Durchläufen der Hauptschleife gefunden wird. Bei allen weiteren
untersuchten Multiplikatoren mit vielen Nullstellen liegt die erforderliche Rechenzeit im
Mittel zwar deutlich unterhalb derjenigen des Standard-Alg., aber für einzelne Zahlen
übersteigt die Anzahl der Hauptschleifen-Durchläufe den Wert von n1/3, so dass man wohl
nicht mehr von einer Variante des Lehman-Verfahren sprechen kann.
Der im Sinne einer Minimierung der Rechenzeit optimale Multiplikator scheint 10.080 zu
sein. Infolge der erhöhten Wirksamkeit dieses Faktors kann die innere (zweite) Schleife beim
Lehman-Verfahren ganz entfallen, so dass sich ein sehr einfacher Algorithmus ergibt:
Algorithmus ’Spitzendetektor’
Eingabe: n (n ungerade, kein Quadrat, keine Primzahl)
fn = 10080 * n: v = 0: m = 1: w = 0
(∗)
Do While w^2 <> m
v = v + fn: u = Int (Sqr(v)) + 1
m = u^2 – v: w = Int (Sqr(m))
Loop
Ausgabe: Teiler sind t1 = ggT(u – w, n) und t2 = n / t1
(Für den o.a. Mersenne-Prüfling werden nur 35 Iterationen benötigt!)
Im Ergebnis wird die Rechenzeit gegenüber der Standard-Variante im Mittel auf weniger als
ein Drittel verkürzt. Zur Verifizierung dieser Aussage ist im Anhang 3 ein unter der im Netz
frei verfügbaren Langzahlarithmetik „ari.bas“ lauffähiges Programm wiedergegeben, in dem
jeweils ein Satz zufällig ausgewählter Zahlen mittels der drei hier behandelten Varianten
(„LEH“, „LEH16“ und „Spitzendetektor“) faktorisiert wird und die benötigten Zyklen und
Rechenzeiten (jeweils Mittelwerte) verglichen werden.
Anmerkungen:
• Die Bezeichnung „Spitzendetektor“ wurde wegen einer naheliegenden ‚graphischen’
Interpretation des Verfahrens gewählt. Diese ist im Beitrag „Über quadratische Reste
und quadratische Kongruenzen“ des Verfassers beschrieben.
•
Beschränkt man n nicht auf Zahlen, deren kleinster Teiler größer n1/3 ist, kann
ggT( u – w, n) = 1 eintreten. In diesem Fall setzt man m = v und fährt mit (*) fort. Bei
der Ermittlung kleiner Teiler ist der Algorithmus – ähnlich wie das Fermat-Verfahren
– allerdings häufig uneffektiv.
•
Wegen des rel. großen Multiplikators ergeben sich ab etwa n > 1012 im Laufe der
Berechnung leicht Zahlen, die die Größenordnung von 1018 überschreiten, so dass man
eine Langzahl-Arithmetik (etwa ‚ari.bas’) verwenden muß.
23
4.4 Das Aussieben geeigneter Faktoren
Die gezielte Suche nach großen Teilern ( n > t1 > n / 2 ) großer Zahlen ist mit den bisher
beschriebenen drei Varianten nicht möglich, da bei diesen das Teilerverhältnis und die erf.
Schrittzahl kaum miteinander korrelieren.
Da gemäß obiger Definition das Teilerverhältnis v für ‚große Teiler’ zwischen 1 und 2 liegt,
müsste die untersuchte Zahl – anstelle mit den Gliedern der Folge 1, 2, 3, 4,... – ausschließlich
mit Zahlen multipliziert werden, die je über mindestens ein Teilerpaar (o, u) verfügen, mit
1 < o / u < 2. Folglich ist eine entsprechende Auswahl aus den zwischen 1 und 2 liegenden
rationalen Zahlen zu treffen. Der unten stehende Algorithmus liefert alle verschiedenen
rationalen Zahlen zwischen h –1 und h mit h = {2, 3, 4,...} in reduzierter Form, bei denen das
Produkt von Zähler und Nenner unterhalb einer Grenze mmax bleibt. Diese Zahlen werden hier
aus naheliegenden Gründen „geeignete Faktoren“ genannt.
Algorithmus GeFak
mmax = 1000 'Vorgabe
h=2
'Vorgabe
IF h MOD 2 = 0 THEN nr = h –1: b = h ELSE nr = h: b = h –1
nb = nr: na = 1: d = 1
FOR i = 1 TO mmax
na = na + 1: nb = nb + b
n1 = na: n2 = nb: f = n1 * n2
IF f > mmax THEN EXIT
IF na MOD 2 = 0 THEN c = 1: r = nr: e = 4 ELSE c = 2: r = 2 * nr: e = 1
d = d + 1: e(d) = e * f
FOR j = 1 TO mmax
n1 = n1 + c: n2 = n2 + r: f = n1 * n2
IF f > mmax THEN EXIT
ed = n2 – n1: ec = n1
DO UNTIL ed = 0: er = ec MOD ed: ec = ed: ed = er: LOOP
gg = ec: IF gg < 2 THEN d = d + 1: e(d) = e * f
NEXT j
NEXT i
e(1) = h –1: ko = d + 1: e(ko) = h
IF e(1) MOD 2 = 0 THEN e(1) = 4 * e(1)
IF e(ko)MOD 2 = 0 THEN e(ko) = 4 * e(ko)
ARRAY SORT e() FOR ko, ASCEND
Es wäre wohl nicht zielführend, dieses Programm im einzelnen zu erläutern. Am leichtesten
dürfte der Zugang sein, wenn man die generierten Zahlen (die Produkte von Zähler und
Nenner) über den dazugehörenden, nach ihrer Größe sortierten rationalen Zahlen (Quotienten
von Zähler und Nenner) grafisch darstellt. Die ’Produkte’ liegen dann auf Parabeln, die
ihrerseits wiederum ihren Ursprung in den ganzzahligen Werten einer Parabel haben. All
diese Parabeln können als die Produkte je zweier Geraden aufgefasst werden; auf der einen
liegen die Zähler auf der anderen die Nenner. Das bildet der obige Algorithmus nach: Die
äußere (i) Schleife berechnet die jeweiligen Startpunkte für die Zähler- und Nenner-Geraden
(j–Schleife). Haben Zähler und Nenner einen ggT größer als 1, wird die betr. Zahl nicht
weiter verwendet. Fallen Zähler und Nenner nicht in die gleiche Restklasse (mod 2), wird das
’Produkt’ aus den bekannten Gründen mit 4 multipliziert. Sodann werden sie als „geeignete
Faktoren“ in einem Vektor e() abgespeichert und abschließend dem Betrag nach aufsteigend
sortiert.
24
Als erstes interessiert natürlich der Zusammenhang zwischen der oberen Grenze mmax und der
Anzahl der unter den genannten Bedingungen möglichen rationalen Zahlen. Die Frage –
etwas allgemeiner formuliert – lautet also: Wie viele unechte (wegen o / u > 1), voll gekürzte
Brüche (o / u) gibt es im Intervall [1, k) mit o⋅u ≤ m max? Klarerweise entspricht die gesuchte
Anzahl der Anzahl Ak echter, voll gekürzter Brüche im Intervall ( 1k , 1] mit o⋅u ≤ m (k ≤ m).
Die Anzahl Qk aller (also einschließlich derer mit ggT(o, u) > 1) Brüche im Intervall mit
o⋅u ≤ m ergibt sich (experimentell) zu Qk ≈ m⋅ln(k) / 2.
Bekanntlich ist die Wahrscheinlichkeit, dass zwei zufällig gewählte nat. Zahlen teilerfremd
sind, gleich ζ (12 ) = π62 = 0,6079271... Das trifft auch zu, wenn die beiden Zahlen aus einem
vorgegebenen Intervall stammen.
ln ( k )
3 ⋅ ln ( k )
= m⋅
Für k = 2 folgt: a 2 = A 2 / m ≈ 0,2106914...
Damit: A k ≈ m ⋅
2 ⋅ ζ( 2)
π2
Wie die nachstehende Tabelle verdeutlicht, liefert die Formel Werte, die sehr nahe an der
tatsächlichen Anzahl geeigneter Faktoren „A 2-Ist“ liegen.
m
A 2-Ist
10
10 2
10 3
10 4
10 5
10 6
10 7
10 8
2
22
211
2112
21070
210695
2106905
21069138
m⋅ln(2)⋅3 / π 2 
2
22
211
2108
21069
210692
2106915
21069148
Anm.: (ohne direkten Zusammenhang mit dem Thema)
Es ist:
m
m
1
1
∑ ϕ(i) / ∑ i ≈ 1 / ζ(2). Die Summe im Nenner ist gleich m (m + 1) / 2; die Summe im
Zähler sei mit Sϕ (m) abgekürzt. Folglich hat man: Sϕ (m) ≈ 3⋅m⋅(m+1) / π 2 (= P). Ist m prim,
gilt Sϕ (m) > P; ist ϕ (m) ≤ m / 4, ist Sϕ (m) < P. Der Wert von Sϕ (m) oszilliert also (mit
immer kleiner werdender rel. Amplitude) um den Wert P. Erstaunlicherweise lässt sich die
Summe der „unberechenbaren“ Eulerschen ϕ -Funktion so einfach und genau abschätzen.
------------------Fazit: Zur Zerlegung einer Zahl n = p i ⋅p j mit p i / p j < 2 mittels des Lehman-Verfahren gibt
es rd. 0,21 ⋅n1/3 geeignete Faktoren f, die für Bildung des Vorfaktors 4⋅f infrage kommen.
Diese können mit dem o.a. Alg. schnell (im Vergleich zur Gesamt-Rechenzeit) bestimmt
werden.
Die nähere Untersuchung zeigt, dass von den so gebildeten Vorfaktoren in der Praxis nur rd.
die Hälfte benötigt wird. Diese wiederum aus den geeigneten Vorfaktoren auszusieben
erübrigt sich, da die nicht benötigten im Wesentlichen zugleich auch die betragsmäßig
größten sind (und die geeigneten Faktoren ja nach aufsteigendem Betrag sortiert wurden).
Am Beispiel: n ≤ 106 => mmax = n1/3 = 100 => aq = 22. Tatsächlich benötigt werden nur 13
Faktoren: 1, 8, 15, 24, 35, 45, 48, 63, 77, 80, 91, 99 und 120; mit diesen können alle Zahlen n
kleiner als 106, mit n = p i ⋅p j und p i / p j < 2, mittels Lehman-Verfahren (ohne Vorfaktor 4,
denn der ist in den o.a. Zahlen schon berücksichtigt) zerlegt werden.
25
Die angegebene Zahlenfolge entspricht genau den ersten Zahlen der Folge der geeigneten
Faktoren, mit der Ausnahme, dass zwischen der 99 und 120 die 112 fehlt, also nicht benötigt
wird.
Fazit: Zur Zerlegung aller hier in Rede stehenden Zahlen reichen rd. n1/3 / 9 Faktoren aus.
Um eine belastbare Aussage zu erhalten, welchen effektiven Vorteil der Einsatz der
„geeigneten“ Vorfaktoren bringt, wurden alle Zahlen n unterhalb von 1010 mit n = p i ⋅p j und
p i / p j < 2 mittels des Standard-Alg., des Spitzendetektors und mit Hilfe der geeigneten
Faktoren zerlegt und die Rechenzeiten verglichen (wobei der Zeitbedarf für die Berechnung
der geeigneten Faktoren mit berücksichtigt wurde). Es ergibt sich folgendes Bild:
Verfahren:
Lehman
Zeitbedarf:
100 %
172 %
Spitzendetektor
Leh + geeignete Faktoren
58 %
100 %
21,5 %
37 %
Der Vorteil ist also durchaus nennenswert, wobei der prozentuale Zeitgewinn mit größer
werdenden Zahlen noch deutlich zunimmt.
(Der Vorteil des Spitzendetektor im Vergleich zu Lehman-Verfahren ist hier deutlich geringer
als der oben (mit rd. drei) angegebene, was der Beschränkung auf Zahlen mit einem
Teilerverhältnis kleiner 2 geschuldet ist.)
26
Anlage 1
Anzahl der Restklassen x mod m, welche als Lösung der Kongruenz x 2 – n ≡ y 2 mod m
bei vorgegebenem n infrage*) kommen.
(Die nachstehenden Angaben und Formeln beruhen auf der Verallgemeinerung
experimenteller Befunde. Beweis?)
Im folgenden wird n als ungerade natürliche Zahl mit ggT(n, m) = 1 vorausgesetzt, d.h.
r = n mod m ist eine prime Restklasse.
Es bedeuten: AQR : Anzahl der quadratischen Reste (Teilmenge der primen Restklassen)
ApR : Anzahl primer Restklassen, bei denen die Menge der Restklassen x die
gleiche Elementanzahl (Ax) besitzt.
Ax : Anzahl der (möglichen) Lösungsrestklassen x mod m
Untersucht werden – je in Abhängigkeit vom Modul m – die Fragen, wie viele
unterschiedliche Ax-Werte es gibt, welche Werte die Ax explizit annehmen und wie viele
prime Restklassen zu den einzelnen Ax-Werten ‚gehören’.
Bei der Beantwortung dieser Fragen spielt die Anzahl AQR der quadratischen Reste modulo m
eine wesentliche Rolle.
α
Die Anzahl AQR(m) der QR ist für m = 2 e ⋅ p1α 1 ⋅ . . . ⋅ p h h
(pi > 2) gegeben durch
h
für
e
<
2
ϕ( m )
h + 1 für e = 2
AQR(m) =
mit f =
h + 2 für e > 2
2f
1.) m ist Primzahlpotenz; m = p k
a) p > 2
Man findet:
ApR
Ax
ϕ (m) / 2
ϕ (m) / 2 – Ck (m)
ϕ (m) / 2
ϕ (m) / 2
Es gibt also jeweils 2 verschiedene Ax-Werte, und diese treffen je für genau die Hälfte der
primen Restklassen zu. Wichtig ist, dass es sich bei den primen Restklassen der ersten Zeile
der Tabelle (ϕ (m) / 2 = AQR ) ausschließlich um quadratische Reste handelt.
Für Ck gilt:
Ck (p k)
k
1
2
3
4
5
6
–1
p–2
p2 – p – 1
p3 – p2 + p – 2
p4– p3 + p2 – p – 1
......
Das ergibt die Formeln für k >1: Ck (p k) =
k ungerade: Ck =
=
=
=
=
ϕ (p) – 1
ϕ (p 2) – 1
ϕ (p 3) + ϕ (p ) – 1
ϕ (p 4) + ϕ (p 2) – 1
k −1
∑ ( − 1) k −1+ i ⋅p i − 2 ( k −1) mod 2
oder auch
i= 1
k / 2 
k/2
i= 1
i= 1
∑ ϕ ( p 2⋅i ) −1 bzw. k gerade: Ck = ∑ ϕ ( p 2⋅i −1 ) −1
-----------------------*) Die im konkreten Fall tatsächlich vorhandene Lösungsmenge hängt von der hier als nicht bekannt angenommenen
Teilerstruktur von n ab.
1
Zwei Beispiele: m = 11 → ϕ (m) = 10, AQR = 5, Ck (11) = – 1
ApR
5
5
Ax
6
5
Die 5 primen Restklassen, die auf Ax = 6 führen, sind die 1, 3, 4, 5, 9
Das sind die qua. Reste mod 11. Im einzeln gilt folgende Zuordnung:
pri. Restkl. x-Restklassen
1 →
1, 2, 4, 7, 9, 10
3 →
1, 2, 5, 6, 9, 10
4 →
2, 3, 4, 7, 8, 9
5 →
3, 4, 5, 6, 7, 8
9 →
1, 3, 5, 6, 8, 10
m = 3 6 → ϕ (m) = 3 6 – 3 5 = 486, AQR = 243, Ck (3 6) = 2 + 18 + 162 – 1 = 181
ApR
243
243
Ax
243 – 181 = 62
243
b) p = 2 → m = 2e → ϕ (m) = 2e – 1, AQR = 2e – 3 für e > 2; AQR = 1 sonst
Da die Aufteilung der Ax nicht in das einfache Schema für p > 2 passt, andererseits eine
Zuordnung der primen Restklassen mod 4 bzw. mod 8 (geschrieben als ‚r(s)’) zu den
x-Restklassen mod 2 bzw. mod 4 möglich ist, erfolgt die Angabe tabellarisch:
e
1
2
3
4
5
ApR
1
1 1(4)
1 3(4)
2
1 3(8)
1 7(8)
4
2 3(8)
2 7(8)
4 1(8)
4 5(8)
4 3(8)
4 7(8)
Ax
1
2 1(2)
2 0(2)
4
2 2(4)
2 0(4)
4
4 2(4)
4 0(4)
8
4
8 2(4)
8 0(4)
e
6
≥7
e
7
8
9
ApR
8 1(8)
8 5(8)
8 3(8)
8 7(8)
2e – 3 1(8)
2e – 3 5(8)
2e – 3 3(8)
2e – 3 7(8)
Ax
8
8
16 2(4)
16 0(4)
Be
2e – 3
2e – 2 2(4)
2e – 2 0(4)
Be
12
16
28
e
10
11
12
Be
48
92
…..
Für die Be gilt die Rekurrenz Be = 2(Be – 1 – 2 1 + e mod 2) mit B6 = 8 und somit
Be = (a + 2e – 3) / 3 mit a = 16 für e ungerade und a = 20 für e gerade.
Bekanntlich sind alle Restklassen r mod 2e für e > 2 quadratische Reste für r ≡ 1 mod 8. Ab
e = 7 weist das zugehörige Ax sich durch den von den übrigen verschiedenen Wert Be aus.
Bemerkenswert ist, dass sich erst ab 27 ein festes Schema bezüglich der Ax einstellt.
2
α
2.) m ist das Produkt von Potenzen ungerader Primzahlen; m = p1α 1 ⋅ . . . ⋅ p h h
Die Lösungen von (quadratischen) Kongruenzen zu einem zusammengesetzten Modul erhält
man bekanntlich (siehe z.B. „Über quadratische Reste und quadratische Kongruenzen“ auf der
Netz-Seite des Verfassers) indem zunächst die Lösungen zu den einzelnen Primfaktoren
bestimmt werden und diese dann mittels des Chinesischen Restsatzes kombiniert werden. Die
gesamte Lösungsanzahl ist das Produkt aus der Anzahl der Lösungen zu den einzelnen
Primzahlpotenzen.
Analog dazu werden vorliegend entsprechend der Beziehung ϕ (m) = AQR⋅2h die ϕ (m)
primen Restklassen in 2h Teilmengen mit der Elementanzahl AQR zerlegt. Die zu diesen
Teilmengen gehörenden Ax erhält man durch Bilden aller möglichen Produkte aus den zu
jedem Faktor p iαi existierenden zwei Ax-Werten, was gerade 2h Werte ergibt.
Am Beispiel: m = 3 3 ⋅5 ⋅11 2 → ϕ (m) = 7920 = 990 ⋅2 3
Die Ax-Werte der Faktoren sind gemäß Ziffer 1): 3 3 5 11 2
4 3 46 ← Ax der qua. Reste
9 2 55
Das ergibt (der Größe nach geordnet) folgende Ax-Werte:
Ax ( zu je 990 primen Restklassen mod m)
4⋅2⋅46 = 368
9⋅2⋅46 = 828
4⋅2⋅55 = 440
9⋅2⋅55 = 990
4⋅3⋅46 = 552
9⋅3⋅46 = 1242
4⋅3⋅55 = 660
9⋅3⋅55 = 1485
Auf diese Weise lassen sich die Ax-Werte zu jedem ungeraden Modul bestimmen. Die
quadratischen Reste führen auch in diesem Fall alle zum gleichen Ax-Wert. Im Beispiel ist das
das Produkt 4⋅3⋅46 = 552.
Nicht bei jedem ungeraden Modul kommen 2h unterschiedliche Ax-Werte vor – sondern in
manchen Fällen gehört das gleiche Ax zu einem Vielfachen von AQR. Dies ist aber nur
scheinbar eine Ausnahme von der Regel, die genau dann auftritt, wenn das betreffende Ax auf
mehrere Arten aus den Faktoren dargestellt werden kann. Z.B.: m = 105 = 3⋅5⋅7 → ϕ (m) =
6⋅8 → AQR = 6
Ax der Faktoren: 3 5
7
1 2
3
Es ist 1⋅3⋅4 = 2⋅2⋅3 = 12; also zwei Darstellungen →
2 3
4
Für Ax = 12 ist ApR = 2⋅AQR = 2⋅6 = 12
-------------------------Anmerkung zu den x-Restklassen
Wie unter 1.a) gezeigt, weisen die ϕ (p k) (nicht unbedingt verschiedenen) Lösungsmengen Lx(r) für
p > 2 nur zwei unterschiedliche Mächtigkeiten auf, und zwar besitzen die Lx(r) für alle r mod p k, die
QR mod p sind, die gleiche Elementanzahl (Ax(QR)) und desgleichen führen die QNR mod p auf
Ax(QNR).
Hinsichtlich der Elemente der Lx(r) fallen folgende Eigenschaften ins Auge:
Insgesamt kommen in den Lx(r) alle Restklassen mod p k mindestens einmal vor (gilt auch für p = 2).
Weiter gilt: x ∈ Lx(r) → m – x ∈ Lx(r) (symmetrische Anordnung, da mit x immer auch – x eine
Lösung der quadratischen Kongruenz ist).
Daraus folgt, dass Ax genau dann ungerade ist, wenn Lx(r) die Restklasse ’0’ enthält, da in diesem Fall
x und m – x mod m identisch sind.
Die Lx(r) mit ungerader Elementanzahl enthalten außerdem alle x mit x ≡ 0 mod p (das sind p k – 1). In
den Lx(r) mit gerader Elementanzahl sind ausschließlich zu p teilerfremde x-Restklassen enthalten.
3
α
3.) Allgemeiner Modul m = 2 e ⋅ p1α 1 ⋅ . . . ⋅ p h h
Zweckmäßigerweise werden zunächst die 2h Ax-Werte des ungeraden Anteils u von m gemäß
Ziffer 2.) berechnet. Die Auswirkungen der Multiplikation mit 2e werden aus Gründen der
Übersichtlichkeit in Tabellenform (die im Wesentlichen eine Kurzform der Tabelle aus Ziffer
1.b) ist) angegeben.
Es sei AQR(2e ⋅u) = fQR ⋅AQR(u); ApR(2e ⋅u) = fpR ⋅ApR(u); Ax (2e ⋅u) = fx ⋅Ax (u)
e
1
2
3
fQR
1
1
1
4
5
2
4
5(8)
6
8
1,5(8)
≥7
2e – 3
1(8)
5(8)
3,7(8)
ApR
16⋅6 = 96
16⋅12 = 192
16⋅6 = 96
16⋅6 = 96
16⋅12 = 192
16⋅6 = 96
32⋅6 = 192
32⋅12 = 384
32⋅6 = 192
1,5(8)
fpR
1
2
2
2
8
4
12
16
16
2e – 3
2e – 3
2e – 2
fx
2
2
4
2
4
4
8
8
16
Be
2e – 3
2e – 2
Beispiel: m = 27 ⋅32 ⋅5 → AQR(u) = 6
ApR(u)
6
12
6
Ax (u)
4
6
9
Es ist 2e – 3 = 16 und B7 = 12
Damit können die Werte für
ApR(m) und Ax (m) berechnet werden
(siehe nachstehende Tabelle).
Ax
12⋅4 = 48
12⋅6 = 72
12⋅9 = 108
16⋅4 = 64
16⋅6 = 96
16⋅9 = 144
32⋅4 = 128
32⋅6 = 192
32⋅9 = 288
4.) Zuordnung vorgegebene prime Restklasse → Ax
Die obigen Ergebnisse ermöglichen die Bestimmung der unterschiedlichen Mächtigkeiten Ax
der potentiellen Lösungsmengen (Restklassen x mod m) und machen Aussagen, wie viele
prime Restklassen den verschiedenen Ax zuzuordnen sind. Darüber hinaus ist aber auch leicht
zu bestimmen, auf welches Ax eine vorgegebene prime Restklasse r = n mod m führt. Z.B.
sei bei dem Modul m = 27 ⋅32 ⋅5 des vorstehenden Beispiels r = 437. Wie groß ist Ax(r) ?
Da die ungeraden Primzahlpotenzen bezüglich der Ax nur danach unterscheiden, ob r
quadratischer Rest bzw. Nichtrest ist, ist je ungeradem Primfaktor das Legendre-Symbol zu
berechnen, und für den geraden Anteil 2e ist festzustellen, in welcher Restklasse modulo 8 der
Rest r liegt.
Vorliegend ist r mod 8 = 5, r mod 3 = 2 (also kein QR) und r mod 5 = 2 (ebenfalls kein QR).
Damit liefert 27 den Faktor 16 (siehe obige Tab.), 32 den Faktor 3 (= ϕ (9) / 2) und 5 den
Faktor 2 (= ϕ (5) / 2).
D.h. beim Rest r = n mod m = 437 sind (von den insgesamt 5760) genau Ax = 16⋅3⋅2 = 96
Restklassen x mod 5760 in Betracht zu ziehen, welche als Lösung der Kongruenz x2 – n ≡ y2
mod m infrage kommen.
4
Anhang 1
Jede Lösung der diophantischen Gleichung n = x2 – y2 (*) kann man trivialer Weise einem
der folgenden vier Fälle zuordnen:
(g,g): x ist gerade und y ist gerade
(g,u): x ist gerade und y ist ungerade
Analog: (u,g) und (u,u)
Beschränkt man sich auf ungerade n kommen nur die beiden Fälle (g,u) und (u,g) in Frage.
Fall (g,u):
Einsetzen von x = 2x’ und y = 2y’ +1 in (*) führt auf n 4+ 1 = x '² − ( y'² + y' ) bzw. (wenn die
beiden Variablen wieder mit x und y bezeichnet werden) auf
x²−
n+1
= y² + y .
4
(**)
Diese Gleichung ist lösbar, wenn (n + 1)/4 eine ganze Zahl ist, wenn also n ≡ 3(4) .
Die Suche nach einer Lösung startet man zweckmäßigerweise mit x o = 12 n + 1  . Die zum
Auffinden einer Lösung erforderliche Schrittzahl ist dann nur halb so groß (im Grenzwert)
wie bei Anwendung von (*); das Teilerpaar (t1,t2) errechnet sich aus t1 = 2(x + y) + 1 und
t2 = 2(x – y) – 1.
Fall (u,g):
Das analoge Vorgehen führt auf x ² + x −
n −1
= y² .
4
(***) Diese Form bezieht sich auf
Zahlen n ≡ 1(4). Es gilt x o = 12 ( n − 1) , t1 = 2(x + y) + 1 und t2 = 2(x – y) + 1.
Wird die gleiche Prozedur auf die Gleichungen (**) und (***) angewandt, erhält man
insgesamt 8 Gleichungen. Zum Modul 8 gibt es 4 ungerade Restklassen. Auf jede dieser
Restklassen entfallen genau 2 der 8 Gleichungen. Diese – und ebenso alle weiteren auf diese
Art erzeugten Gleichungen – sind von folgender Form:
2 ( k − 2) ⋅ x ² + a ⋅ x −
n+r
2k
= 2 ( k − 2) ⋅ y ² + b ⋅ y
(****)
In (**) und (***) ist k = 2; in der darauffolgenden Stufe ist k = 3, u.s.w. Die drei Größen a, b
und r lassen sich unter Verwendung der Abkürzung h = 2(k – 2) für die jeweils nächste Stufe
rekursiv leicht bestimmen:
(g,g):
(g,u):
(u,g):
(u,u):
a <== a;
a <== a;
a <== 2h + a;
a <== 2h + a;
b <== b;
b <== 2h + b;
b <== b;
b <== 2h + b;
r <== r
r <== r + 2k ⋅ (h + b)
r <== r – 2k ⋅ (h + a)
r <== r + 2k ⋅ (b – a)
Abschließend: k <== k + 1 h = 2h. Die Restklasse mod 2k, für die die betr. Gleichung
„zuständig“ ist, folgt natürlich sofort aus der Größe r.
Beispiel: Aus (**) soll die im Fall (u,u) gültige Gleichung entwickelt werden.
k = 2: a = 0; b = 1; r = 1; h = 1. Es folgt
k = 3: a = 2⋅1 + 0; b = 2⋅1 + 1; r = 1 + 22⋅(1 – 0) = 5. n + 5 ist genau dann durch 23
teilbar, wenn n ≡ 3(23). Für diese lautet also eine der beiden Gleichungen:
2x² + 2x –
n+ 5
8
= 2y² + 3y
(Wie sich zeigt, lassen sich mit dieser Gleichung sogar alle Teilerpaare der Zahlen
n ≡ 3(8) bestimmen.)
1
Praktisch anwendbar zur
Der Startwert für x ist x o =  ( k1−1) ( n + r + a 2 − a )
 2

Teilersuche sind die Gleichungen natürlich nur, wenn es ein einfaches Kriterium gibt, das
entscheidet, ob ein vorgelegtes x die betr. Gleichung erfüllt. Dieses Kriterium ist vorhanden: x
ist genau dann eine Lösung, wenn der Term d = 2k ⋅m + b2 ein Quadrat – also d = w2 – ist,
wobei der Wert der linken Seite von (****) mit ‚m’ abgekürzt wurde.
Hat man ein d = w2 gefunden, errechnet sich das zugehörige Teilerpaar t1⋅t2 = n zu
t1 = 2(k – 1)⋅x + a + w und t2 = 2(k – 1)⋅x + a – w. [Also n = (2(k – 1)⋅x + a) 2 – w 2 ]
Nun stellt sich natürlich die Frage, inwieweit das Verfahren geeignet ist, die Anzahl der
Iterationen („Schrittzahl“) des Basis-Algorithmus zu reduzieren. Für k = 2 wurde oben bereits
gesagt, dass die Schrittzahl halbiert wird und man beim Übergang zu k = 3 für jede der 4
ungeraden Restklassen von 23 zwei Gleichungen erhält. Das ist bei jeder weiteren Erhöhung
von k so; die Anzahl der je Restklasse zu lösenden Gleichungen beträgt somit 2(k – 2). Da die
Schrittzahl je Gleichung sich gegenüber Basis-Algorithmus gleichzeitig ungefähr auf den 2(k –
1)
ten Teil reduziert, ergibt sich gegenüber k = 2 keine Verbesserung mehr (was auch nicht
überrascht).
Die weitere Prüfung zeigt allerdings, dass die gemäß dem o.a. Verfahren gebildeten
Gleichungen nicht alle benötigt werden, denn alle Gleichungen, in denen der Wert von a
derselbe ist, liefern die gleichen Teilerpaare der vorgelegten Zahl n. Es ist daher einfach, die
überflüssigen Gleichungen auszusortieren. Die nachstehende Tabelle zeigt in Abhängigkeit
von k, wie viele Gleichungen tatsächlich benötigt werden. Dabei gibt es bemerkenswerte
Unterschiede je nach dem zu welcher Restklasse mod 8 die zu zerlegende Zahl gehört.
k:
2
3
4
5
6
7
8
9
10
n ≡ 1(8):
5(8):
3,7(8):
1
1
1
2
2
1
2
2
2
4
2
4
4
4
8
6
8
16
8
16
32
14
32
64
24
64
128
Für Zahlen n ≡ 3(4) ist also ab k = 3 keine Verbesserung mehr möglich; für n ≡ 5(8) liegt die
Schwelle bei k = 5. Dagegen scheint die Zunahme an Gleichungen für n ≡ 1 (8) auch für
große k immer unterhalb einer Verdoppelung zu bleiben; allerdings ist der Gewinn ab k = 10
nicht mehr nennenswert.
Im folgenden sind – als Auswahl der zahlreichen Varianten (gleiche a-Werte) – für k = 4 die
maßgeblichen Größen r, a und b (siehe (****)) der 2 je prime Restklasse mod 16
erforderlichen Gleichungen angegeben.
Die letzte Spalte zeigt, zu welcher Restklasse mod 16 die beiden Teiler (eines Paares)
gehören, die von der betreffenden Gleichung gefunden werden. Ihr Produkt muss natürlich die
in der ersten Spalte angegebene Restklasse ergeben.
2
n(16)
r
a
b
{t1,t2} mod 16
1
–1
– 49
1
7
0
0
1/1, 9/9, 5/13,
3/11, 7/7, 15/15
3
–3
13
2
6
1
7
1/3, 9/11
5/7, 13/15
5
–5
11
3
5
2
6
1/5, 9/13
3/7, 11/15
7
–7
9
4
0
3
3
1/7, 9/15
3/13, 5/11
9
–9
7
5
3
4
4
1/9, 5/5, 13/13
3/3, 7/15, 11/11
11
–11
5
6
2
5
3
1/11, 3/9
5/15, 7/13
13
–13
3
7
1
6
2
1/13, 5/9
3/15, 7/11
15
–15
49
4
0
1
7
3/5, 11/13
1/15, 7/9
Insgesamt ist es erstaunlich, dass die mehrfache Anwendung der nun wirklich trivialen
Information „Die Lösung ist entweder gerade oder ungerade“ eine wesentliche Verminderung
des Aufwandes zur Teilerbestimmung bewerkstelligen kann.
Der Algorithmus (zum Experimentieren; hier am Beispiel n ≡ 1 mod 16; erste Zeile):
Vorgabe: n (≡ 1 mod 16)
k = 4: a = 1: b = 0: r = – 1
k0 = 2^k: k1 = k0 div 2: k2 = k1 div 2
x = int ((sqr (n + r + a^2) – a) / k1): nr = (n + r) div k0
m = k2 * x^2 + a * x – nr: d = 0: w = 1
do while d <> w^2
m = m + k2 * (2 * x + 1) + a
d = k0 * m + b^2: w = isqrt(d)
x=x+1
loop
c = k1 * x + a
Ausgabe: t1 = c + w: t2 = c – w (falls die beiden Teiler in den o.a. Restklassen liegen.)
3
Eine effektive Nutzung für die Faktorisierung ist dann nur möglich, wenn alle Gleichungen,
die die betr. Zahl erfüllen können, simultan abgearbeitet werden. Das ist ohne weiteres
möglich, wie das nachstehende Beispiel zeigt, wobei auf die o.a. Darstellung
n = (2(k – 1)⋅x + a) 2 – w 2 zurück gegriffen wird:
Eingabe: n (≡ 5 mod 16 oder ≡ 9 mod 16)
k = 4: a = 3: a2 = 5
k1 = 2^(k–1): f2 = 2 * k1 * (a2 – a): e2= a2^2 – a^2
x0 = INT ((SQR (n + 1 – a^2) – 1) / k1)
FOR x = x0 + 1 TO n
s = k1 * x + a
m = s^2 – n: y = INT (SQR (m))
IF y^2 = m THEN PRINT “Teiler: ”;s + y; s – y: EXIT
m2 = m + f 2 * x + e2: y2 = INT (SQR (m2))
IF y2^2 = m2 THEN PRINT “Teiler: “;s – a + a2 + y2; s – a + a2 – y2: EXIT
NEXT x
Der Algorithmus benötigt also nur die beiden für die Restklasse 5(16) und 9(16) zuständigen
a-Werte (siehe obige Tabelle); der Wert von m2 wird zur Vereinfachung aus m berechnet.
Fazit:
Jede zusammengesetzte ungerade Zahl besitzt für alle k mit 2 k < n Darstellungen als
n = (2 k – 1 ⋅x + a) 2 – y 2
(0 ≤ a < 2 k–1 )
wobei a nur von den Restklassen modulo 2 k der beiden Faktoren 2 k –1⋅x + a + y und
2 k –1⋅x + a – y abhängt.
4
Anhang 2
Serieller Einsatz von Vorfaktoren
DEFEXT V-Z
DEFQUD A-U
DIM a(1 TO 83000,1 TO 3) AS LONG
DIM v(1 TO 63000000,0 TO 5) AS LONG
'=========================================
'0. Vorgaben: n,i0,f0,dd,vmax (ganzzahlig)
'z.B.:i0=5*10^2:f0=1*10^6:dd=40:vmax=3
---------------------------------------wn=SQR(n)
im=INT(wn*(SQR(vmax)+1/SQR(vmax)-2)/2)+1:PRINT im 'Schrittzahl Basis-Alg.
'1. Belegung der Ränder des Intervalls [1,v-max]
f=1:ru=f0:z=1+i0/wn
i..:Schrittzahl
vo=(z+SQR(z^2-1))^2:ro=INT(vo*f0)
ii :Schrittz.-Summe
v(ru,0)=1:v(ru,3)=i0:v(ru,4)=1:v(ru,5)=1:ii=i0
si :Belegungs-Summe
FOR j=ru TO ro:v(j,1)=ro:v(j,2)=ru:NEXT j:si=ro-ru
w..:Quadrat-Wurzel
f=vmax:ro=f*f0:z=1+i0/(wn*SQR(f))
wvu=SQR(f)*(z-SQR(z^2-1)):vu=wvu^2:ru=INT(vu*f0)
v(ru,0)=f: v(ru,3)=i0: v(ru,4)=f: v(ru,5)=1: ii=ii+i0
FOR j=ru TO ro:v(j,1)=ro:v(j,2)=ru:NEXT j:si=si+ro-ru+1 'For..Next: von f
IF si=>(vmax-1)*f0 THEN END
'belegten Bereich in v(,) markieren
'2. Erzeugung der Vorfaktoren f = c*s (v= c/s)
FOR s=2 TO 10^12
FOR c=s+2 TO vmax*s-2 STEP 2
IF c MOD 4=2 AND s MOD 4=2 THEN ITERATE 'ITERATE: Vorfaktor wird verworfen
ed=s:ec=c:DO UNTIL ed=0:er=ec MOD ed:ec=ed:ed=er:LOOP
ggt=ec: IF ggt>2 THEN ITERATE 'ggT-Berechnung
f= c*s
'3. Berechnung des von f belegten v-Intervalls sowie der Schrittzahl
wvk=SQR(c/s): rv=INT(wvk^2*f0)
IF v(rv,1)>0 THEN ITERATE
IF v(rv-dd,1)>0 AND v(rv+2*dd,1)=0 THEN ITERATE
IF v(rv+dd,1)>0 AND v(rv-2*dd,1)=0 THEN ITERATE
wf=wn*SQR(f): z=1+i0/wf
wvo=wvk*(z+SQR(z^2-1)): vo=wvo^2:ro=INT(vo*f0)-1
wvu=wvk*(z-SQR(z^2-1)): vu=wvu^2:ru=INT(vu*f0)+1
'3a. Fallunterscheidung (aa = 1, 2, 3, 4)
FOR e=1 TO 1
IF v(ro,1)=0 AND v(ru,1)=0 THEN aa=1 'Bereich komplett frei
IF v(ro+dd,1)>0 AND v(ru-dd,1)>0 THEN aa=2:ro=ro+dd:ru=ru-dd:EXIT
IF v(ro+dd,1)>0 AND v(ru-dd,1)=0 THEN aa=3:ro=ro+dd:EXIT
IF v(ro+dd,1)=0 AND v(ru-dd,1)>0 THEN aa=4:ru=ru-dd:EXIT
IF v(ro,1)>0 AND v(ru,1)>0 THEN aa=2 'Belegung überlappt beidseitig
IF v(ro,1)>0 AND v(ru,1)=0 THEN aa=3
IF v(ro,1)>0 AND v(ru-dd,1)>0 THEN aa=2:ru=ru-dd:EXIT
IF v(ro,1)=0 AND v(ru,1)>0 THEN aa=4
IF v(ro+dd,1)>0 AND v(ru,1)>0 THEN aa=2:ro=ro+dd
NEXT e
SELECT CASE aa
CASE 1
v(ru,0)=f: v(ru,3)=i0:v(ru,4)=c: v(ru,5)=s:ii=ii+i0
FOR j=ru TO ro:v(j,1)=ro:v(j,2)=ru:NEXT j:si=si+ro-ru+1
CASE 2
ru1=v(ru,1)+1:DO WHILE v(ru1,1)>0:ru1=v(ru,1)+1:ru=v(ru1,2):LOOP
ro1=v(ro,2)-1:DO WHILE v(ro1,1)>0:ro1=v(ro,2)-1:ro=v(ro1,1):LOOP
wvo=SQR((ro1+2)/f0):y=wvo/wvk+wvk/wvo-2:iho=INT(y*wf/2)+1
wvu=SQR((ru1-2)/f0):y=wvu/wvk+wvk/wvu-2:ihu=INT(y*wf/2)+1
ih=MAX(iho,ihu)
v(ru1,0)=f: v(ru1,3)=ih: v(ru1,4)=c: v(ru1,5)=s: ii= ii+ih
FOR j=ru1 TO ro1:v(j,1)=ro1:v(j,2)=ru1:NEXT j:si=si+ro1-ru1+1
1
CASE 3
ro1=v(ro,2)-1:DO WHILE v(ro1,1)>0:ro1=v(ro,2)-1:ro=v(ro1,1):LOOP
wvo=SQR((ro1+2)/f0):y=wvo/wvk+wvk/wvo-2:ih=INT(y*wf/2)+1:z=1+ih/wf
wvu=wvk*(z-SQR(z^2-1)):vu=wvu^2:ru=INT(vu*f0)
v(ru,0)=f: v(ru,3)=ih: v(ru,4)=c: v(ru,5)=s: ii= ii+ih
FOR j=ru TO ro1:v(j,1)=ro1:v(j,2)=ru:NEXT j:si=si+ro1-ru+1
CASE 4
ru1=v(ru,1)+1:DO WHILE v(ru1,1)>0:ru1=v(ru,1)+1:ru=v(ru1,2):LOOP
wvu=SQR((ru1-2)/f0):y=wvu/wvk+wvk/wvu-2:ih=INT(y*wf/2)+1:z=1+ih/wf
wvo=wvk*(z+SQR(z^2-1)):vo=wvo^2:ro=INT(vo*f0)
v(ru1,0)=f: v(ru1,3)=ih: v(ru1,4)=c: v(ru1,5)=s: ii= ii+ih
FOR j=ru1 TO ro:v(j,1)=ro:v(j,2)=ru1:NEXT j:si=si+ro-ru1+1
END SELECT
IF si=>(vmax-1)*f0 THEN EXIT,EXIT
NEXT c
NEXT s
'4. Fertig; Darstellung der Ergebnisse, Belegung
a=0
FOR o=f0 TO vmax*f0
IF v(o,0)<>0 THEN a=a+1:a(a,1)=v(o,0):a(a,2)=v(o,3)+1:a(a,3)=v(o,5)
'Speichert f, Schrittzahl, s in der Matrix a(,)
NEXT o
PRINT "n= ";n, "Schritte Basis-Alg./red. Schrittzahl: ";INT(im/ii)
PRINT "Anzahl Vorfak.:"; a,"Max. Vorfak.:";c"*";s;"=";f
'Kontrolle, ob alle v-Werte (überlappend) belegt sind
FOR h=1 TO a:'PRINT ,,,a(h,1),a(h,2),a(h,3)
z=1+a(h,2)/(wn*SQR(a(h,1))):wz=SQR(z^2-1):wv=SQR(a(h,1))/a(h,3)
wvo=wv*(z+wz):vo=wvo^2:wvu=wv*(z-wz):vu=wvu^2
IF vd-vu<0 AND h>1 THEN PRINT vo,vu,vd-vu;"Fehler!"
vd=vo
NEXT h
END
2
Anhang 3
Vergleich von Varianten des Lehman-Verfahren (Kurzbeschreibung ist unten angefügt)
function le(mi: integer);
var
n0,n,n1,n2,n3,n6,n16,nw,nu,nr,nz,v,v1,v2,i,j,g,b,k: integer;
u,ug,og,m,x,d,c,fn: integer;
t: real;
e: array[5011]
begin
#--------------------Teil 1--------------------------------------n0: = 10**mi; b: = 1000; nw: = isqrt(n0); nu: = floor(n0**(1/3));
random_seed(666); nr: = nw – nu; i: = 0;
while i < b + 10 do
v1: = random(nr); v1: = v1 + nu; n1: = next_prime(v1,0);
v2: = n0 div n1; n2: = next_prime(v2,0); n: = n1 * n2;
if n1 <> n2 then i: = i+1; e[i]: = n; end;
end;
#-------------------LEH -------------------------------------t:= timer(); c:=0;
# c zählt die Anzahl der erf. Rechenzyklen
for k:=1 to b do
n:=e[k]; n3:=floor(n**(1/3)); n6:=isqrt(n3)+1;
g:=4*n; fn:=0; j:=0; i:=1;
while j=0 do
fn:=fn+g; ug:=isqrt(fn)+1;
d:=4*isqrt(i); og:=ug+floor(n6/d); i:=i+1;
for u:=ug to og do
m:=u**2-fn; x:=isqrt(m); c:=c+1;
if m=x**2 then v1:=gcd(u-x,n); v2:=n div v1; j:=1; break; end;
end;
end;
end;
writeln("LEH: ",floor(c/b)," Zyklen (Mittelw.)");
writeln("Zeit: ",floor((timer()-t)/1000)," Sek.");
#-------------------LEH16---------------------------------------t: = timer(); c: = 0;
for k: = 1 to b do
n: = e[k]; n3: = floor(n**(1/3)); nz: = floor(n3/64);
n6: = isqrt(n3); j: = 0; n16: = 16 * n;
for i: = 1 to nz do
fn: = n16 * i; ug: = isqrt(fn) + 1; d: = 8 * isqrt(i); og: = ug + floor(n6 / d);
for u: = ug to og do
m: = u**2 – fn; x: = isqrt(m); c: = c + 1;
if m = x**2 then
v1: = gcd(u + x, n); v2: = n div v1; j: = 1; nz: = n3; break;
end;
end;
if j=1 then break; end;
end;
1
for i:=nz+1 to n3 do
fn:=n16*i; u:=isqrt(fn)+1; m:=u**2-fn; x:=isqrt(m); c:=c+1;
if m=x**2 then v1:=gcd(u+x,n); v2:=n div v1; break; end;
end;
end;
writeln("LEH16 ",floor(c/b)," Zyklen (Mittelw.)");
writeln("Zeit: ",floor((timer()-t)/1000)," Sek.");
#-------------------Spitzendetektor-------------------------------t: = timer(); c: = 0;
for k: = 1 to b do
n: = e[k]; fn: = n * 10080; v: = 0; m: = 0; x: = 1;
while m <> x**2 do
v: = v + fn; u: = isqrt (v) + 1;
m: = u**2 – v; x: = isqrt(m); c: = c + 1 ;
end;
v1: = gcd (u – x, n); v2: = n div v1;
end;
writeln("Spitz.: ",floor(c/b)," Zyklen (Mittelw.)");
writeln("Zeit: ",floor((timer()-t)/1000)," Sek.");
#----------------------------------------------------------------end.
Erläuterung: Lautet die Start-Eingabe z.B. „ le(12).“, wird in Teil 1 ein Satz von 1000 Zahlen
der Größenordnung 1012 generiert, die das Produkt von 2 Primfaktoren sind. Der kleinere der
beiden Primfaktoren wird dabei ‚zufällig’ aus dem Intervall [1012/3, 1012/2] ausgewählt.
Speicherung der Zahlen im Vektor e[ ]. (Wählt man den Exponenten > 21 – etwa „ le(22).“ –
sollte man etwas Zeit zur Verfügung haben.)
Anschließend werden die 1000 Zahlen mit den 3 o.a. Varianten faktorisiert, wobei die erste
(LEH) das Standard-Verfahren beinhaltet.
Der Vorteil von „Spitz.“ gegenüber LEH wächst (im Mittel) mit dem Teilerverhältnis. Wählt
man z.B. das Teilerverhältnis ‚zufällig’ aus dem Intervall [1, n1/3] und bestimmt daraus die
beiden Teiler so, dass ihr Produkt möglichst nahe an 10x liegt, steigt der Zeitvorteil auf über
das fünffache an.
2