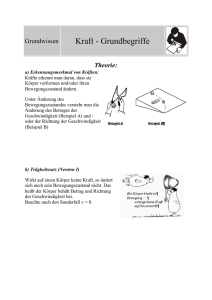
272. Die Skizze stellt den Verlauf der Schiene einer
Werbung

272. Die Skizze stellt den Verlauf der Schiene einer Loopingbahn dar. Im Punkt A hat der Wagen die Geschwindigkeit 6,1 m/s. Im Punkt C soll er einer Zentrifugalkraft vom 1,5fachen Betrag seiner Gewichtskraft ausgesetzt sein. Der Punkt C befindet sich in der Höhe hC = 22 m über dem Boden. Der Wagen wird als Massepunkt aufgefasst, von der Reibung ist abzusehen. a) Beschreiben Sie die Energiezustände in den Punkten A, B, C und die Energieumwandlungen bei der Bewegung des Wagens von A nach C. b) Berechnen Sie die Höhe hA des Punktes A über dem Boden. c) Berechnen Sie die Geschwindigkeit, mit der dieser Wagen den Punkt B, der sich in Bodenhöhe befindet, passiert. d) Geben Sie die im Punkt B auf die Schiene wirkende Gesamtkraft als Vielfaches der Gewichtskraft des Wagen an. 329. Eine Schaukel schwingt aus horizontaler Anfangslage als Pendel nach unten. Welche Kraft haben die masselos gedachten Streben der Gondel am tiefsten Punkt auszuhalten, wenn die Masse der Gondel 60 kg und die der darin sitzenden Person 70 kg beträgt? 133. Die Kurve einer Rennbahn soll bei einem Kurvenradius von 50 m für die Geschwindigkeit 36 km/h gebaut werden. Welche Neigung der Bahn ist optimal? 272. Die Skizze stellt den Verlauf der Schiene einer Loopingbahn dar. Im Punkt A hat der Wagen die Geschwindigkeit 6,1 m/s. Im Punkt C soll er einer Zentrifugalkraft vom 1,5fachen Betrag seiner Gewichtskraft ausgesetzt sein. Der Punkt C befindet sich in der Höhe hC = 22 m über dem Boden. Der Wagen wird als Massepunkt aufgefasst, von der Reibung ist abzusehen. a) Beschreiben Sie die Energiezustände in den Punkten A, B, C und die Energieumwandlungen bei der Bewegung des Wagens von A nach C. b) Berechnen Sie die Höhe hA des Punktes A über dem Boden. c) Berechnen Sie die Geschwindigkeit, mit der dieser Wagen den Punkt B, der sich in Bodenhöhe befindet, passiert. d) Geben Sie die im Punkt B auf die Schiene wirkende Gesamtkraft als Vielfaches der Gewichtskraft des Wagen an. 329. Eine Schaukel schwingt aus horizontaler Anfangslage als Pendel nach unten. Welche Kraft haben die masselos gedachten Streben der Gondel am tiefsten Punkt auszuhalten, wenn die Masse der Gondel 60 kg und die der darin sitzenden Person 70 kg beträgt? 133. Die Kurve einer Rennbahn soll bei einem Kurvenradius von 50 m für die Geschwindigkeit 36 km/h gebaut werden. Welche Neigung der Bahn ist optimal? Lösungen 272. geg.: v A = 6,1 ms ges.: FC = 1,5FG hc = 22m Lösung: a) Energieumwandlungen: Der Wagen kommt vom Punkt an, in dem er bereits eine Geschwindigkeit besitzt. Damit hat er dort kinetische und potentielle Energie. Der Boden wird als Bezugslinie angenommen. Damit besitzt er im Punkt B nur noch kinetische Energie, die genau so groß wie die Summe der Energien im Punkt A ist (Energieerhaltung) Diese kinetische Energie im Punkt B wird wieder in potenzielle Energie umgewandelt, wenn der Wagen zum Punkt C fährt. Da nicht alles umgewandelt wird, besitzt er dort wieder kinetische und potenzielle Energie. b) Als Bedingung muss gelten, dass im Punkt A so viel Energie vorhanden ist, dass der Wagen im Punkt C mit der entsprechenden Radialkraft herumschleudert. EKinA + EpotA = EkinC + EkinC m 2 m ⋅ v A + m ⋅ g ⋅ hA = ⋅ v 2C + m ⋅ g ⋅ hC 2 2 Welche Geschwindigkeit ist im Punkt C notwendig? Die Radialkraft soll das 1,5 fache der Gewichtskraft betragen. Also: FR = 1,5m ⋅ g m ⋅ v c2 = 1,5m ⋅ g r Der Radius ist die Hälfte der Höhe zum Punkt C. 2 ⋅ m ⋅ v c2 = 1,5m ⋅ g hC 2 ⋅ m ⋅ v c2 = 1,5m ⋅ g ⋅ hC v 2c = 3 ⋅ g ⋅ hC 4 Das wird in die Energiegleichung eingesetzt, aus der vorher noch die Masse m gekürzt wurde. 1 2 1 3 ⋅ g ⋅ hC ⋅ v A + g ⋅ hA = ⋅ + g ⋅ hC 2 2 4 3 ⋅ g ⋅ hC 1 g ⋅ hA = + g ⋅ hC − ⋅ v 2A 8 2 hA = 3 ⋅ hC ⋅ v2 + hC − A 8 2⋅g ( ) 2 6,1 ms 3 ⋅ 22m hA = + 22m − 8 2 ⋅ 9,81 m2 s hA = 8,25m + 22m − 1,9m hA = 28,35m c) Die Geschwindigkeit im Punkt B ergibt sich aus der Energie im Punkt A, die hier vollkommen in kinetische Energie umgewandelt wurde. EkinB = EkinA + EpotA m 2 m 2 ⋅ vB = ⋅ v A + m ⋅ g ⋅ hA 2 2 1 2 1 2 ⋅ v B = ⋅ v A + g ⋅ hA 2 2 2 vB = v 2A + 2 ⋅ g ⋅ hA vB = v 2A + 2 ⋅ g ⋅ hA vB = 24,36 ms d) Die Gesamtkraft im Punkt B berechnet sich aus der schon vorhandenen Gewichtskraft und der Radialkraft, da sich der Wagen an dieser Stelle auf der Kreisbahn befindet. m ⋅ vB2 r v2 F = m⋅ g + B r 24,36 ms F = m ⋅ 9,81 m2 + s 11m F = m ⋅ 63,8 m2 F = m⋅g + ( ) 2 s Antwort: Die normale Gewichtskraft ist die Masse mal die Fallbeschleunigung. Der Wert 63,8 ist 6,5 mal größer als die Fallbeschleunigung, so dass im Punkt B der 6,5 fache der Gewichtskraft wirken. Der Punkt A muss sich 28,35 m über dem Boden befinden. Durch den Punkt B donnert der Wagen mit 24,4 m/s. Dabei spüren die Insassen das 6,5 fache der eigenen Gewichtskraft. 329. geg.: ges.: m G = 60 kg F mP = 70 kg Lösung: Die Streben müssen im untersten Punkt zwei Kräfte aufbringen: die Gewichtskraft und die Radialkraft. F = FG + FR Die Gewichtskraft ist: FG = m ⋅ g Die Radialkraft: FR = m⋅ v 2 r r ist der Radius der Kreisbewegung und entspricht der Länge der Schaukel. Die ist aber nicht gegeben. v ist die Geschwindigkeit, die die Schaukel im untersten Punkt hat. Da sie aus der horizontalen Lage kommt, in der sie in Ruhe war, entspricht die Geschwindigkeit der Fallgeschwindigkeit aus dieser Höhe. Die Höhe ist aber der Radius. v = g⋅ t und g s = ⋅t2 2 t= 2⋅s g Damit wird: v = g⋅ 2⋅s g v = 2⋅s⋅g v = 2 ⋅r ⋅ g Damit geht man in die Gleichung der Radialkraft: m ⋅ 2 ⋅r ⋅ g r FR = 2 ⋅ m ⋅ g FR = Die Länge der Schaukel ist nicht notwendig. Nun lässt sich die Gesamtkraft berechnen: F = m⋅ g + 2 ⋅m ⋅ g F = 3 ⋅m⋅ g F = 3 ⋅130 kg ⋅ 9,81 m2 s F = 3826 N F = 3,8 kN Antwort: Die Streben müssen einer Belastung von 3,8 kN widerstehen können. Das ist das dreifache der Gewichtskraft der Person. 133. geg.: r = 50 m ges.: α v = 36 km h Lösung: Optimale Kurvenneigung heißt, dass das Fahrzeug ohne Reibung mit dieser Geschwindigkeit durch die Kurve fahren kann. Dabei ist wichtig, wie das Auto auf die Unterlage wirkt. Nur wenn die resultierende aller Kräfte senkrecht auf den Boden drückt, bleibt es in der Kurve. Ansonsten kann es nach oben oder nach unten wegrutschen. Fährt das Auto in eine Kurve, spürt es zwei Kräfte: Die senkrecht nach unten wirkende Gewichtskraft FG und die senkrecht zum Erdboden nach außen wirkende Zentrifugalkraft FZ. Diese ist eine Trägheitskraft und vom Betrag her genau so groß wie die Radialkraft. Beide Kräfte zusammen ergeben eine resultierende Kraft FR, die schräg nach unten zeigt. Ohne jegliche Reibung würde diese Kraft das Auto aus der Kurve tragen. Durch die Reibung zwischen Rädern und Straße bleibt es aber in der Kurve. Optimal wäre es, wenn die Kraft senkrecht auf den Untergrund wirken würde. Dann spürt auch der Fahrer keine Seitenkräfte, was es für ihn wesentlich angenehmer macht. Wie stark muss nun geneigt werden? Der Winkel zwischen Boden und Straße taucht, wie in der Zeichnung zu sehen, in dem Kräfteparallelogramm auf. Da ein schönes rechtwinkliges Dreieck vorliegt, gilt: tan α = FZ FG Damit lässt sich der gesuchte Winkel berechnen: tan α = m⋅ v2 r ⋅m ⋅ g tan α = v2 r⋅ g tan α = m 10 s 2 50m ⋅ 9,81 m s2 α = 11,5° Antwort: Die optimale Bahnneigung beträgt 11,5°.