12-3 Gravitation
Werbung

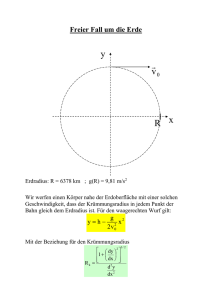
LZ F12.3/B12.6 Gravitation 6. 1 Gravitation 6.1. Einleitung 6.1.1 Geschichtlicher Hintergrund ca. 2700 v.u. Z. ca. 350 v.u. Z. ca. 265 v.u. Z. ca. 220 v.u. Z. ca. 150 1543 1600 1609 1609 1687 1809 1859 1915 1923 Sternbilder erhalten Namen Aristoteles: Kugelgestallt der Erde Aristarch von Samos: spricht vom heliozentr. Weltbild Eratosthenes: Berechnung des Erdumfangs Ptolemaios: Begründer des geozentr. Weltbildes Copernicus: Begründung des heliozentr. Weltbildes G. Bruno: Bekenntnis zum heliozentr. Weltbild – Inquisition/Scheiterhaufen Kepler: Gesetze der Planetenbewegung Galilei: intensive Himmelsbeobachtung – Inquisition Newton: Gravitationsgesetz für Planetenbewegung Gauß: Methode zur Berechnung der Planetenbahnen Kirchhoff: Begründer der Spektralanalyse Einstein: Relativitätstheorie Hubble: misst Galaxienentfernung 6.1.2. Astronomische Daten und deren frühere Messung Vermessung des Sonnensystems 6.1.2.1. Geographische Länge / Geographische Breite Die geographische Länge wird als Winkelmaß ausgehend vom Nullmeridian angegeben. Die geographische Breite ist die im Winkelmaß angegebene nördliche oder südliche Entfernung eines Ortes der Erdoberfläche vom Äquator. Gegenüber der Angabe im Dezimalsystem erfolgt jedoch die Angabe im Sexagesimalsystem (Grad, Minute, Sekunde; 1° ̂ 60') Kelheim: Längengrad Breitengrad 11.8667° / 11° 52' 0'' 48.9167° / 48° 55' 0'' Ein Sterntag (eine Erdrotation um die eigene Achse) hat 23 Stunden 56 Minuten. Da sich die Erde während ihrer Eigenrotation auf der Bahn um die Sonne weiter bewegt, sieht man am nächsten Tag die Sonne 4 Minuten später (1 Sonnentag hat 24 Stunden)! Bestimmung der Längengrade: genaue Uhr; Kenntnis der Zeit von Greenwich Bildquelle: http://www.kowoma.de/gps/astronav/laenge_mittagsmethode.htm LZ F12.3/B12.6 Gravitation 2 6.1.2.2. Bestimmung des Erdradius und -umfang 150 Jahre nach Aristoteles machte der Grieche Eratosthenes folgende Überlegung die im Prinzip richtig war. Die Entfernung Alexandrien - Assuan beträgt 850 km; Die Sonnenstrahlen verlaufen angenähert parallel! Am 21.6. sieht man die Sonne im Wasser des Brunnens sich spiegeln und zur gleichen Zeit wirft der Obelisk in Alexandrien einen Schatten mit einem Winkel von 7,5° Mit diesen Daten kann man den Erdumfang und -radius berechnen. 3600 : 7,50 = 48; u = 48 · 850 km = 40800 km mit u 2 rE rE u 6494km 2 ( genauer Wert rE 6386km ) Von Pythagoras wird berichtet, dass er der Ansicht war, dass die Erde der Mittelpunkt der Welt sei und dass sie Kugelgestalt hat. 200 Jahre später: Aristoteles 384 - 322 v. Chr. erkannte, dass bei Mondfinsternis der Schatten den die Erde auf den Mond wirft immer kreisförmig ist! Heutige Verfahren: fotografisch und mit Radarverfahren von Satelliten aus vermessen. 6.1.2.3. Bestimmung des Abstandes Erde-Mond Im 18. Jahrhundert wurde die Entfernung zum Mond trigonometrisch bestimmt. In Berlin (geogr. Breite φ1 = 52,52°) wie auch am Kap der Guten Hoffnung (geogr. Breite φ2 = –33.93°), die auf demselben Längenkreis liegen, wurde der Mond zur selben Zeit angepeilt. Es ergaben sich δ1 = 57,92° und δ2 = 34,28°. Nordpol Berlin δ1 zum Mond φ1 Äquator φ2 δ2 Kap Südpol Quelle: Müller-Fonfara: Mathematik verstehen, Falken-Verlag, 1994, S. 326 Mittlerer Mondbahnradius RM = 384 · 103 km = 60,3 · rE 1969 Astronaut Armstrong: Spiegel auf Mond - Radarsignal E-M-E Messung der Laufzeit - daraus Entfernung auf 10cm genau berechnet! LZ F12.3/B12.6 Gravitation 3 6.1.2.4. Bestimmung des Mondradius 1m 1cm Scheibe Mond Auge RM Aus bekannter Mondentfernung: Mondradius bestimmbar rM R M 0,5cm 1m rM 1738km ; rM 0,273 rE 6.1.2.5. Entfernung der Sonne (Erdbahnradius) nach Aristarch von Samos Bei Halbmond stehen die Linien a und b genau senkrecht aufeinander. Der Winkel wurde mit = 87° gemessen. Das Prinzip ist richtig. Der errechnete Wert von rE war jedoch ungenau. Tatsächlicher Winkel = 89°51´ RE = 149,6 · 106 km 6.1.2.6. Sonnenradius Die Sonne erscheint am Himmel so groß wie der Mond (Sonnenfinsternis) bekannt : Abstand Erde Mond, Monddurchmesser, Erdbahnradius. Erde RM Mond Sonne RE Sonnenradius: rS 109 rE Ähnlich wurden die Daten der Planeten bestimmt. Mit dem freien Auge sind 5 Planeten sichtbar: Merkur - Venus - Mars - Jupiter - Saturn + Mond und Sonne ...........heilige Zahl 7: später entdeckt: 1781 Uranus, 1840 Neptun, 1930 Pluto, ? LZ F12.3/B12.6 Gravitation 4 6.1.3. Die Keplerschen Gesetze, Weltbilder Kosmos....gr. Weltall; gea....gr. Erde, centrum....lt. Mittelpunkt 6.1.3.1. Geozentrisches Weltbild von Ptolemaios (85- 165 n.Chr.) Im Mittelpunkt der Welt befindet sich die kugelförmige Erde Die Hohlkugel der Fixsternsphäre ist so weit von der Erde entfernt, dass die Fixsterne nur als Punkte erkennbar sind. Die Fixsternsphäre dreht sich im Laufe eines Tages einmal um die Erde. Sonne, Mond und die Planeten beschreiben Bahnen, die sich aus Kreisbahnen zusammensetzen lassen. Ptolemaios bevorzugte die Kreisbahn als die vollkommene Bahn, die den himmlischen Gestirnen am besten angemessen ist! Dieses Weltbild blieb fast 1500 Jahre unverändert Die Kinematik der Planetenbewegung war jedoch kompliziert. Nachdem das Fernrohr erfunden wurde, beobachtete Galilei (Prof. in Pisa), dass die Venus manchmal als Sichel erkennbar war. Er folgerte, dass sie sich um die Sonne drehen muß. Auch die anderen Planeten drehen sich um die Sonne. 6.1.3.2. Heliozentrisches Weltbild von Kopernikus und Kepler helios....gr Sonne Die Sonne ruht im Mittelpunkt des Weltalls Die Erde ist ein Planet Die Planetenbewegung wird durch die Keplerschen Gesetze beschrieben. Der Fixsternhimmel ruht. Die Erde rotiert im Laufe eines Tages einmal um ihre Drehachse. Nikolaus Kopernikus: Domherr in Frauenburg, 1473 - 1543; „Über die Bewegung der Himmelskörper“ Tycho Brahe (Däne) war Hofastronom bei Kaiser Rudolf II Johannes Kepler (1571 - 1630) war Gehilfe und Nachfolger von Brahe. Er diente drei Kaisern in Prag: Rudolf II, Mathias und Ferdinand II. Zugleich war er Professor in Linz. Lebte auch zeitweise in Regensburg. Er starb bei einem Besuch in Regensburg, als er vom Kaiser wiederholt sein Gehalt einforderte (Reichstag - Reformationszeit) Aus dem riesigen Zahlenmaterial und der Aufgabe der Kreisbahn (Aristoteles) nahm er als Bahn die Ellipsenform an. Er hatte damit Erfolg und schrieb darüber zwei Bücher. 1609... „Neue Astronomie“; 1619... „Die Harmonie der Welt“ LZ F12.3/B12.6 Gravitation 5 6.1.3.3. Die drei Gesetze von Kepler 1. Kepler-Gesetz: Gesetz von der Gestalt der Bahn Die Planeten bewegen sich auf elliptischen Bahnen, in deren einem Brennpunkt sich die Sonne befindet. Perihel P Sonnennähe 2. Kepler-Gesetz: Sonne Aphel A Sonnenferne Gesetz der Flächen Der von der Sonne nach einem Planeten gezogene Ortsvektor überstreicht in gleichen Zeiten gleiche Flächen. v v 3. Kepler-Gesetz: Gesetz der Umlaufzeiten Die Quadrate der Umlaufzeiten T zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen a der Bahnellipsen Halbachsen = mittlere Entfernung von der Sonne - in Näherung = Kreisbahnen! a R 2 3 T1 R1 T2 R2 T2 CS konst. R3 T ... Umlaufdauer; R ... mittlerer Bahnradius CS ... Keplerkonstante des Sonnensystems Die Konstante C ist für alle Satelliten (Planeten, ...), die dasselbe Zentralgestirn umlaufen, gleich. z.B.: Die Erde ist Zentralgestirn für den kreisenden Mond und für die Satelliten. Die Sonne ist Zentralgestirn für alle Planeten des Sonnensystems. LZ F12.3/B12.6 Gravitation 6 6.1.3.4. Aufgaben und Übungen LB. S. 220 Nr. 1 Weitere Aufgaben 1.1 Berechnen Sie aus der Umlaufzeit des Merkur und den Bahnradien des Mars und Merkur die Umlaufzeit des Mars! Wie verhalten sich die Bahngeschwindigkeiten von Merkur und Mars zueinander? 1.2 (1,88a; ca. 2:1) Berechnen Sie die Konstante CS des 3. Kepler Gesetzes für die Sonne als Zentralgestirn aus der Bewegung des Merkur um die Sonne! 2.1. Berechnen Sie die Konstante CE des 3. Kepler Gesetzes für die Erde als Zentralgestirn aus der Bewegung des Mondes um die Erde! 2.2. Was lässt sich über diese Konstante CE für künstliche Erdsatelliten aussagen? Der erste künstliche Erdsatellit, Sputnik I, hatte eine Umlaufdauer von 96 Minuten. Berechnen Sie seinen mittleren Bahnradius! 2.3. Welche mittlere Bahngeschwindigkeit hatte Sputnik I ? ( 9,9 1029 a 2 m3 ; 7,0 106 m; 7,6km s 1 ) 3.0. Ein künstlicher Satellit umläuft die Erde in der Zeit T nahezu auf einer Kreisbahn. 3.1. Von welchen weiteren Größen hängt der mittlere Abstand h (Höhe) von der Erdoberfläche ab? Stellen Sie die Funktion h(T) in Form einer Gleichung auf! 3.2. Welche Umlaufzeit muss demnach ein Erdsatellit mindestens haben? 3.3. In der Nähe der Erdoberfläche ist die Fallbeschleunigung 9,8m s 2 . Die in 3.2. berechnete Umlaufzeit erhält man auch, wenn man ansetzt, dass die Gewichtskraft des Erdsatelliten zugleich die Zentralkraft ist. Berechnen Sie auch auf diese Art die Mindestumlaufdauer eines Erdsatelliten! (1,4h; 1,4h) LZ F12.3/B12.6 Gravitation 7 6.2. Das Gravitationsgesetz von Newton 6.2.1 Herleitung des Gravitationsgesetzes Sir Isaac Newton: Anekdote - Newton sitzt unter einem Apfelbaum und beobachtet das Herunterfallen eines Apfels. Warum fällt der Mond nicht auf die Erde? Die wirksame Zentralkraft die den Mond auf seine Umlaufbahn zwingt ist die gleiche Kraft, die einen fallenden Apfel zu Boden beschleunigt. Die Ursache dieser ist Kraft die Eigenschaft aller Körper sich anzuziehen - Gravitationskraft. Aus der Mondbewegung, den Gesetzen der Kreisbewegung, den Newtonschen Gesetzen und dem 3. Kepler-Gesetz Schlussfolgerung auf die Planetenbewegungen! 4 2 Newton war bekannt: FZ m aZ mit aZ r r 2 T bekannte Daten des Mondes: RM , TM , mM 2 Theoretische Überlegung: 4 2 FZ mM RM 2 TM TM 2 2 3 mit 3. Kepler-Gesetz CE 3 bzw. TM CE RM RM 4 2 4 2 1 FZ mM RM mM CE RM3 CE RM2 FZ ~ mM mit 4 2 = konstant CE 1 RM2 Mit dem 3. Satz von Newton (Wechselwirkungsgesetz) folgt: mE FME FEM mM FME = - FEM FME = FEM RM 1 1 FME ~ mE 2 2 , so ist RM RM 1 1 F G mE mM 2 und damit folgt: F ~ mE mM 2 RM RM ist FZ FEM ~ mM allgemein FG G m1 m2 r2 G ... Gravitationskonstante, Naturkonstante LZ F12.3/B12.6 Gravitation 8 6.2.2. Bestimmung der Gravitationskonstanten G - nach Cavendish (1731 - 1810) (Beschleunigungsmethode) 6.2.2.1. Aufbau der Gravitationsdrehwaage und Herleitung Newton war es mit den damaligen experimentellen Einrichtungen nicht möglich die Gravitationskonstante G zu ermitteln. Erst 1798 gelang es Cavendish mit der unten beschriebenen Methode diese Konstante zu ermitteln. Spiegel, Torsionsfaden m2 m1 FG FDrill Skala 0 Lichtzeigereinrichtung m1 = 1,5g; m2 = 1,5kg Ausgangspunkt der Messung: Nullpunkt für Lichtzeiger wird markiert, wenn angelegte große Kugeln und kleine bewegliche Kugeln (hängen mit einer Stange an einem Torsionsfaden) im Gleichgewicht sind. Es gilt: FDrill = FG ; FG ... Gravitationskraft, FDrill ... Torsionskraft s S l L ... ... ... ... Weg der kleinen Kugel Lichtzeigerweg Kugelabstand von der Achse Abstand Spiegel/Schirm m1 ... Masse der kleinen Kugel m2 ... Masse der großen Kugel r ....... Anstand der beiden Kugeln vor Beginn der Bewegung s S und tan 2 und mit der Näherung: für sehr klein gilt: tan 2 2 tan l L S l s S s folgt: Weg der kleinen Masse 2 L l 2 L Es gilt tan LZ F12.3/B12.6 Gravitation 9 Erschütterungsfreies Umlegen der großen Kugeln um 1800. Die kleinen Kugeln werden zu den großen Kugeln hin beschleunigt! Es gilt zu Beginn des entstehenden Einschwingvorganges: FBeschl 2 FG a S l L t2 m1 m2 m m m1 a 2 G 1 2 2 2 r r G a r2 2 m2 FBeschl = FDrill + FG mit FDrill = FG a 2 und mit s t 2 und s S l 2 S l a 2 L 2 L t2 mit FBeschl m1 a und FG G G S l r2 2 L t 2 m2 Experimentelle Ermittlung: Die Beschleunigung wird zu Beginn des Einschwingvorgangs experimentell ermittelt. Die Schwingungsdauer des Systems beträgt T 10 Minuten, so dass von 0 bis t1 = 0,1·T die Bewegung als gleichmäßig beschleunigt angesehen werden kann. a = konstant 6.2.2.2. Auswertung einer Messung Messtabelle t s 0 15 30 45 60 75 90 S cm 0 0,30 1,00 2,00 3,10 5,10 7,30 s 105 m 0 t2 s2 0 Hausaufgabe: Berechnen Sie mit Hilfe der Formel von Seite 8 unten , den Lichtzeigerweg auf dem Schirm S, in den „Fallweg“ s der kleiner Kugeln um. Gegeben sind weitere Daten der Versuchseinrichtung: 1 = 5,0cm; r = 4,6cm; L = 5,3m; Tragen Sie s in Abhängigkeit von t2 in folgendes Diagramm ein und ermitteln Sie daraus zeichnerisch die Beschleunigung a. LZ F12.3/B12.6 Gravitation 10 Auswertung mit Hilfe des Graphen: t 2 s Diagramm Folgerung: s t2 ; a r2 m ; mit G G= s2 2 m2 a mit s t 2 a 2 genauer Wert: absoluter Fehler: Bedeutung der Steigung .............................................. G= 1011 m3 kg 1 s2 G= 6,673 · 1011·m3 ·kg 1·s 2 1011·m3 ·kg 1·s 2 G = relativer Fehler in Prozent: Übung: LB.S. 220 Nr. 2 G = GSoll = % (= GSoll) LZ F12.3/B12.6 Gravitation 11 6.2.4 Anwendungen des Gravitationsgesetzes 6.2.4.1 Berechnung von Satellitenbahnen Satellitenbahnberechnungen beruhen auf der Überlegung von Newton, dass die Gravitationskraft diejenige Kraft ist, die Satelliten in die Kreisbahn „zwingt“. Vereinbarung über die Radienschreibweise: r ... Radius des Himmelskörpers R ... Bahnradius des Himmelskörpers FZ FG Ansatz: mZ mS RS 2 4 2 mZ 2 G TS RS 3 mS RS S 2 G TS 2 4 2 CZ RS 3 G mZ TS 2 RS 3 G mZ Keplerkonstante CZ Umlaufdauer TS 2 T RS 3 S G mZ 2 Bahnradius RS mZ 4 2 RS 3 G TS 2 Masse mZ des zentralen Gestirns Bahngeschwindigkeit vS : Ansatz: FZ FG vS 2 m m mS G Z 2 S R RS G mZ vS RS „Erdnähe“; 1. Kosmische Geschwindigkeit Der Bahnradius eines Satelliten ist RS rE h . Für h rE kann in Näherung RS rE gesetzt werden. Es ist dann die Gravitationskraft auf der Erdoberfläche gleich der Gewichtskraft! vS 2 Fg FZ mS g mS vS g rE rE vS 7,90 km s1 1. Kosmische Geschwindigkeit Mindestgeschwindigkeit für einen Satelliten, damit er sich auf einer Kreisbahn um die Erde bewegt! Übung: Berechnen Sie die Gravitationskraft auf der Erdoberfläche und die Gewichtskraft, die auf einen Probekörper der Masse m = 1,00 kg wirken. Vergleiche beide Werte durch Berechnung der Abweichung in 0/00 . LZ F12.3/B12.6 Gravitation 12 geostationäre Bahn; „Synchronsatellit“ Ein Synchronsatellit (Satelliten für Nachrichtenübertragung) der in der Äquatorebene um die Erde kreist, erscheint einem Beobachter auf der Erde „stillstehend“, d.h. er hat die gleiche Winkelgeschwindigkeit. N Beobachter Satellit Äquatorebene h S Übung: Berechnen Sie den Bahnradius eines Synchronsatelliten und seine Höhe über dem Äquator! 6.2.4.2 Gravitationsfreier Punkt zwischen zwei Massen – 1. Lagrange-Punkt Im „Gravitationsfreier“ Punkt P heben sich die Gravitationskräfte beider Massen auf einen Probekörper auf, d.h. die resultierende Kraftwirkung ist Null. m1 ; m2 verursachen die Gravitationskräfte; m1 ; m2 mP ... Probekörper F1P F2 P m1 F1P ... Kraft von Körper 1 auf m2 Probekörper in P mP F2 P ... Kraft von Körper 2 auf P Probekörper in P r2 r1 r Es gilt: (1) r r1 r2 F1P F2P (2) Übung: 1. bzw. G m1 mP m m G 2 2 P 2 r1 r2 Zeigen Sie, das folgende Gleichung gilt: r2 r [alternative Lösung: r1 2. 3. 1 m1 1 m2 m1 r r m1 m2 aus AP FOS 1973/AII] m1 m2 Berechnen Sie den gravitationsfreien Punkt im System Erde-Mond mit m1 mE ; m2 mM ; mE 81,3 mM ; r RM 60,3 rE . [Ergebnis: 1. r1 =54,3· rE ; r2 =6,0· rE 2. r1 =67,8· rE ; r2 = -7,5· rE ] Interpretieren Sie die Ergebnisse. LZ F12.3/B12.6 Gravitation 13 6.2.4.3 Massenbestimmung von Himmelskörpern Die Fallbeschleunigung auf dem Himmelskörper ist bekannt mP FG g Auf der Erdoberfläche eines Himmelskörpers wirkt auf einen Probekörper die Gewichtskraft, die gleich groß wie die Gravitationskraft im Anstand rE ist. Fg FG mZ mS RS 2 g RS2 mZ G mS g G Übung: Berechnen Sie damit die Masse der Erde und machen Sie die Einheitenkontrolle! [ mE 5,96 1024 kg ] Ermittlung der Masse eines Himmelskörpers der einen Trabanten (z.B. Mond) besitzt mZ Übung: 1. 2. 4 2 RS 3 4 2 (Herleitung siehe 6.2.4.1) G C Z G TS 2 Berechnen Sie die Masse der Sonne! [ mS 2,00 1030 kg ] Berechnen Sie die Masse der Erde mit den Daten des Mondes! Zweikörperproblem - Massenbestimmung des Mondes Da die Fallbeschleunigung des Mondes nicht bekannt war und der Mond auch keinen Begleiter hat, sind die bereits genannten Methoden zur Massenbestimmung des Mondes nicht geeignet. Da die Mondmasse gegenüber der Erdmasse bei der Bewegung dieses Zwei-Massen-Systems um die Sonne, nicht vernachlässigt werden kann, wird diese Tatsache zur Massenbestimmung des Mondes verwendet. Von der Sonne aus gesehen, bilden Erde und Mond eine „Gesamtmasse“. Diese Masse mit dem gemeinsamen Schwerpunkt S bewegt sich auf einer Kreisbahn (angenähert Erdbahnradius RE ) um die Sonne. Beide Himmelskörper wirken jeweils mit dem gleichen Betrag der Gravitationskraft aufeinander. Sie stürzen nicht aufeinander, da sie sich um den gemeinsamen Schwerpunkt S drehen und dadurch eine Fliehkraft erhalten die betragsgleich den Gravitationskräften ist. LZ F12.3/B12.6 Gravitation 14 RE Bahn des Schwerpunktes um die Sonne Erde Mond S FFE FME FEM FFM r2 r1 RM FFE = FME FFM = FEM FME = FEM = FG 4 2 4 2 mit TE TM m r M 2 TE 2 TM 2 mE r2 Hebelgesetz: mM r1 mE r1 FFE = FFM mE r1 mM r2 Die Abstände (Radien) vom gemeinsamen Schwerpunkt S verhalten sich umgekehrt wie die Massen der beiden Körper! Aufstellen des Gleichungssystems: (1) (2) mE r1 mM r2 RM r1 r2 (3) FME FEM FG G (4) FFM FG (5) FFM mM r2 Übung: mE mM RM 2 4 2 TM 2 RM 3 4 2 mE G TM 2 1. Zeigen Sie, dass für die Masse des Mondes gilt: mM 2. Berechnen Sie mit Hilfe der Gleichungen (1) und (2) jeweils die Abstände r1 und r2 ! Gegeben sind: mE ; mM ; RM [ r1 4700km , d.h. der Schwerpunkt liegt noch innerhalb des Erdkörpers] LZ F12.3/B12.6 Gravitation 15 6.2.4.4. Beschleunigung auf der Oberfläche von Himmelskörpern; Gravitationsfeldstärke Die Gravitationskraft, mit der ein Körper von einem Himmelskörper angezogen wird, ist abhängig vom Abstand zu seinem Massenmittelpunkt und seiner Masse. Diese Kraft sorgt gleichzeitig für die Beschleunigung ( ̂ Gravitationsfeldstärke) zu seinem Massenmittelpunkt. Fa FG mZ mK RS 2 m a(RS ) G Z2 RS mK a(RS ) G Übung: Berechnen Sie die Oberflächenbeschleunigung auf dem Mars, dem Mond, der Sonne und dem Jupiter! 6.2.4.5. Aufgaben und Übungen LB. S. 220 Nr. 3;4;5 6 7 8;9 11 12;13;14 - Bahn- und Massenberechnung; Gravitationsgesetz - Gravitationsfreier Punkt - Fallbeschleunigung - Bahn- und Massenberechnung; Fallbeschleunigung - Fallbeschleunigung - Bahn- und Massenberechnung; Gravitationsgesetz Aufgaben: 1.0 1.1 2.0 2.1 2.2 3.1 Mit dem Hubble Space Telescope (HST) können Fotoaufnahmen ferner Himmelsobjekte in bislang unerreichter Qualität gemacht werden.. Das HST umläuft die Erde einmal in 96,7 min auf einer kreisähnlichen Bahn. Berechnen Sie die mittlere Flughöhe über der Erdoberfläche und die durchschnittliche Bahngeschwindigkeit. ( 6,1102 km; 7,56km s1 ) Der deutsche Wissenschaftssatellit ASTRO-SPAS umlief die Erde auf einer Kreisbahn in 300km Höhe. Berechnen Sie die Umlaufzeit und die Bahngeschwindigkeit. Vergleichen Sie letztere mit der Schallgeschwindigkeit. (90,3min; 7,73 km s1 ; 23fach) Um wie viel Prozent ist die Gravitationsfeldstärke in dieser Höhe geringer als an der Erdoberfläche in Deutschland? (8,8%) Berechnen Sie die 1. Kosmische Geschwindigkeit für den Planeten Mars! (3,55km·s1 ) Abschlussprüfungsaufgaben FOS 1984/I FOS 1997/II FOS 1992/III FOS 1998/I FOS 1994/I FOS 1996/II LZ F12.3/B12.6 Gravitation 16 Abschlussprüfung 1986 - Nachtermin 1.0 Es wird angenommen, dass eine Raumfähre radial von der Erde wegfliegt. In der Fähre wird mit Hilfe eines Fallversuches der Betrag der Fallbeschleunigung g(h) in Abhängigkeit von der Höhe h bezüglich der Erdoberfläche untersucht. In den Messintervallen t kann die jeweilige Fallbeschleunigung als konstant angesehen werden, die Reibungskräfte sind vernachlässigbar klein. Für die Fallzeit t der Kugel in Abhängigkeit von der Höhe h ergibt sich folgende Messreihe: Messung Nr. 1 0,00 h in rE t in s 0,451 Dabei ist rE der mittlere Erdradius. 2 0,50 0,677 3 1,00 0,903 4 2,50 1,58 1.1.1 Warum setzt eine sinnvolle Versuchsdurchführung voraus, dass die Raumfähre während jeder Messung jeweils mit konstanter Geschwindigkeit fliegt? (3BE) 1.1.2 Beschreiben Sie die Durchführung des Versuchs. (5BE) 1.2 Berechnen Sie für die Höhen von 1.0. jeweils den Betrag der Fallbeschleunigung g(h) und zeigen Sie, dass für h 0 g(h) nicht direkt proportional zu 1.3.0 Bezogen auf den Erdmittelpunkt muss gelten: g(r) ~ 1 ist. h2 (6BE) 1 . r2 1.3.1 Bestätigen Sie diesen Zusammenhang durch graphische Auswertung der Messreihe. Maßstab: 1 m , 2 = 1cm 2 10cm; 100 rE s (6BE) 1.3.2 Ermitteln Sie unter Verwendung Ihres Diagramms von 1.3.1 die Höhe über der Erdoberfläche, in welcher der Betrag der Fallbeschleunigung 4,9 m ist. s2 1.3.3 Bestimmen Sie mit Hilfe der Messung Nr. 4 die Masse mE der Erde. (6BE) (4BE) Arbeitszeit ca. 55 Minuten; Punkte 30 gesamt Abschlussprüfungsaufgaben Lösungen: 3 1996: 1.3 k=3,6·108 m s ; 1,9·1027kg; 1.4.1 1,6·108m; 28,2 km·s-1 1.5.1 3. Kepler-Gesetz 1.5.2 6,60·1010J 1997: 1.2 6,39·1023kg; 1.3.2 6,69·107J; 1.4.2 2,69·1010J 29 Punkte, 52 Minuten. 27 Punkte; 49 Minuten 1994: 2.2 7,68 km·s-1; 8,73 m·s-2; 2.3.2 3,07 km·s-1; 42,2·103km 2.3.3 1,41·1010J; 2.4.1 24,5·103km; 2.4.2 1,91·104s 33 Punkte; 60 Minuten 1998: 1.1 FG=FZ; 1.2 1,988·1030kg; 1.3 273,5Nkg-1; 1.4.1.87,9d; 1.4.2 Energie nicht im LP 31 Punkte; 55 Minuten *********************** Ende Kapitel 6. ************************** 2016-01-19