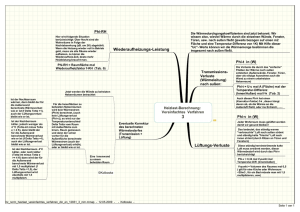
Anwendung und Analyse strahlbasierter Messmethoden am

Zentrum für
Synchrotronstrahlung
Diplomarbeit an der Fakultät Physik
der Technischen Universität Dortmund
Anwendung und Analyse strahlbasierter
Messmethoden am Speicherring DELTA
Helge J. Rast
26. März 2010
Inhaltsverzeichnis
1. Einleitung
1
2. Grundlagen der Strahloptik
5
2.1. Beschleunigung und Ablenkung . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2. Koordinatensystem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3. Strahlführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3.1. Magnetfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3.2. Elemente der Strahlführung . . . . . . . . . . . . . . . . . . . . . .
8
2.4. Bewegung entlang des Sollorbits . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4.1. Bewegungsgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.4.2. Lösung der Bewegungsgleichung für Einzelteilchen . . . . . . . . . 11
2.4.3. Betatronschwingung . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.5. Störungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.5.1. Dipolstörungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.5.2. Quadrupolstörungen . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.6. Hysterese . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3. DELTA
19
3.1. Magnetstruktur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1.1. Triplettstruktur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.1.2. Magnettypen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3.2. Diagnose- und Korrektursysteme . . . . . . . . . . . . . . . . . . . . . . . 26
3.2.1. Strahllagemonitore . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.2.2. Orbitkorrektur und Sollorbit
. . . . . . . . . . . . . . . . . . . . . 28
3.2.3. Relais-Kaskade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.2.4. Kontrollsystem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.2.5. Induktive Wegaufnehmer
. . . . . . . . . . . . . . . . . . . . . . . 30
3.3. Thermische und mechanische Einflüsse auf die Quadrupole . . . . . . . . . 31
3.3.1. Thermische Ausdehnung der Quadrupole . . . . . . . . . . . . . . . 31
3.3.2. Translation der Quadrupole . . . . . . . . . . . . . . . . . . . . . . 33
III
Inhaltsverzeichnis
3.3.3. Messung der thermischen Ausdehnung und Verschiebung . . . . . . 34
3.3.4. Aufstellungsfehler der Quadrupole . . . . . . . . . . . . . . . . . . 36
4. Strahlbasierte Messmethoden
39
4.1. Bestimmung von Offsets der Strahllagemonitore . . . . . . . . . . . . . . . 39
4.1.1. Strahlbasierte Methode . . . . . . . . . . . . . . . . . . . . . . . . 39
4.2. Bestimmung von Quadrupolfehlaufstellungen . . . . . . . . . . . . . . . . 42
4.2.1. Modellbasierte Methode . . . . . . . . . . . . . . . . . . . . . . . . 42
4.2.2. Korrektorbasierte Methode . . . . . . . . . . . . . . . . . . . . . . 45
5. Diskussion und Analyse der verwendeten Messmethoden
49
5.1. Strahlbasierte Methode zur Bestimmung von Offsets der Strahllagemonitore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
5.1.1. Einfluss eines zeitlich konstanten Dipolkorrektorfeldes . . . . . . . 50
5.1.2. Einfluss eines zeitlich veränderlichen Dipolkorrektorfeldes . . . . . 51
5.2. Modellbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
54
5.2.1. Einfluss von Magnetfeldern unterschiedlicher Ordnung . . . . . . . 54
5.2.2. Größenordnung des Einflusses der Sextupolmagnete . . . . . . . . . 56
5.2.3. ∆k-Abhängigkeit der bestimmten Fehlaufstellung . . . . . . . . . . 57
5.2.4. Genauigkeit und Iterative Anwendung der modellbasierten Messmethode an DELTA . . . . . . . . . . . . . . . . . . . . . . . . . . 58
5.3. Korrektorbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen 59
5.3.1. Einfluss von Magnetfeldern unterschiedlicher Ordnung . . . . . . . 60
5.3.2. Bestimmung der zur ∆k-Kompensation nötigen Korrektorstärke . . 61
5.3.3. Genauigkeit
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
6. Messergebnisse und Bewertung der Messmethoden
6.1. Iterative Anwendung der modellbasierten Methode am Triplett „qf03+06“
67
67
6.1.1. Iterative Korrektur der Fehlaufstellung . . . . . . . . . . . . . . . . 69
6.1.2. Ergebnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
6.1.3. Erster Test der korrektorbasierten Methode . . . . . . . . . . . . . 72
6.2. Anwendung der korrektorbasierten Methode am Triplett „qf03+02“ . . . . 72
6.2.1. Korrektur der Fehlaufstellung . . . . . . . . . . . . . . . . . . . . . 73
6.2.2. Ergebnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6.3. Vergleich der Messmethoden . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6.3.1. Genauigkeit der Bestimmung der Fehlaufstellung . . . . . . . . . . 75
6.3.2. Genauigkeit der Bestimmung von xc . . . . . . . . . . . . . . . . . 76
IV
Inhaltsverzeichnis
6.4. Auswirkung der Korrektur der Fehlaufstellungen . . . . . . . . . . . . . . 79
6.4.1. Reduktion der integralen Korrektorstärke . . . . . . . . . . . . . . 79
6.4.2. Lokalität der Korrektorentlastung
. . . . . . . . . . . . . . . . . . 80
6.5. Bewertung der Messmethoden . . . . . . . . . . . . . . . . . . . . . . . . . 82
7. Zusammenfassung
83
A. Messergebnisse der modellbasierten Methode
87
B. Abbildungen
91
V
1. Einleitung
In einem Speicherring können hochenergetische geladene Teilchen durch magnetische
Felder auf einer geschlossenen Bahn geführt und über längere Zeit stabil eingeschlossen bzw. gespeichert werden. Diese Teilchen (z.B. Ionen oder Elektronen) stehen dann
für interne bzw. externe Wechselwirkung mit Gas oder fester Materie in so genannten
Target-Experimenten zur Verfügung. Speichert man zwei Strahlen mit nicht notwendigerweise gleicher Energie und Teilchensorte gegenläufig, so kann man die Teilchen auch an
ausgezeichneten Punkten kollidieren lassen. Man spricht dann von einem Collider. Die
vorgenannten Experimente finden überwiegend im Bereich der Hadronen-, Kern- und
Teilchen-(Hochenergie-)physik statt.
Im Fall gespeicherter ultrarelativistischer Elektronen mit Energien größer als etwa
100 MeV bis hin zu einigen GeV ist man heute mehrheitlich an der externen Nutzung
von Synchrotronstrahlung interessiert. Diese entsteht, wenn Elektronen sehr hoher kinetischer Energie senkrecht zu ihrer Bewegungsrichtung durch magnetische Felder abgelenkt
werden. Da diese Strahlung erstmals an einem Synchrotron beobachtet wurde [4], wird
sie Synchrotronstrahlung genannt. Durch ihre besonderen Eigenschaften kann die Synchrotronstrahlung für viele Anwendungen, wie z.B. festkörperphysikalische Experimente
der Oberflächen- und Kristallstrukturanalyse, genutzt werden. Die Strahlung ermöglicht
darüber hinaus Einblicke in die elektronische Struktur von kondensierter Materie, leistet
entscheidende Beiträge im Bereich der Werkstoffanalytik und Werkstoffkunde und findet
ihre Anwendungen in der Bildgebung der Medizin. Synchrotronstrahlungsquellen der 3.
Generation werden ausschließlich zur Erzeugung von Synchrotronstrahlung eingesetzt. In
ihnen befinden sich spezielle Magnetstrukturen. Diese werden „Insertion Devices“ genannt
und erzeugen Synchrotronstrahlung sehr hoher Intensität und Qualität.
DELTA1 ist eine solche Synchrotronstrahlungsquelle der 3. Generation. Elektronen
können mit einer Energie von bis zu 1,5 GeV bei Strahlströmen von (100 − 130) mA über
Stunden stabil gespeichert werden. Die Anlage besteht aus einem 75 MeV Linearbeschleuniger Linac als Injektor, dem Boostersynchrotron BoDo, in dem die Elektronen auf die
Endenergie beschleunigt werden und dem eigentlichen Speicherring DELTA. Der Umfang
beträgt 115 m, die Umlaufszeit der Elektronen 0,384 µs. Zur Führung der Teilchen auf
1
DELTA ist ein Akronym für „Dortmunder ELekTronenspeicherring-Anlage
1
Kapitel 1. Einleitung
der geschlossenen Bahn werden magnetische Dipole, zur transversalen Fokussierung der
Teilchen magnetische Quadrupole eingesetzt. Diese besitzen ein linear mit dem Abstand
von der Strahlachse anwachsendes magnetisches Feld, welches rücktreibende Kräfte auf
die Elektronen ausübt. In den Speicherring sind drei Insertion Devices eingebaut (siehe Abb. 1.1). Es handelt sich hierbei um zwei Undulatoren (U55 und U250) und einen
supraleitenden Wiggler (SAW) [22].
BL1
BL2
BL3
BL4
U250
BL5
(FEL)
Gun
Linac
BL0
BL6
BL12
BL11
BoDo
Delta
U55
BL10
BL9
BL8
SAW
BL7
Abbildung 1.1.: Aufbau der Synchrotronstrahlungsquelle DELTA, bestehend aus einem
Linearbeschleuniger (Linac), dem Boostersynchrotron BoDo und dem Speicherring DELTA. Eingezeichnet sind die drei eingebauten Insertion Devices (U55, U250, SAW [22]),
die zur Erzeugung sehr intensiver Synchrotronstrahlung genutzt werden. Über die 12 Beamlines (BL) wird die erzeugte Synchrotronstrahlung zu den Experimentierplätzen geführt.
Die Qualität des Elektronenstrahls einer Synchrotronstrahlungsquelle ist derart hoch,
dass die Querdimensionen des Strahls weniger als 1 mm, oft auch weniger als 100 µm
betragen. Die herausragenden Eigenschaften der Synchrotronstrahlung (kleine Emissionsfläche bei kleinen Winkeldivergenzen) können daher nur zum Tragen kommen, wenn
der Strahl selbst sich auf der Sollposition innerhalb des Rings befindet. Dies gilt insbesondere für die Orte der Strahlungserzeugung, also die „Insertion Devices“. Feld- und
Aufstellungsfehler der magnetischen Elemente bedingen jedoch eine Strahllage, die von
der Solllage des Strahls (Sollorbit) abweicht. Über den Ring verteilte Dipolkorrektoren
sorgen dann für eine entsprechende Korrektur. Die Größe der notwendigen Korrektur
hängt notwendigerweise insbesondere von Ort und Größe der Fehlaufstellungen ab. Dies
2
gilt im Besonderen für die Quadrupole, da deren magnetische Achse mit dem Sollorbit
zusammenfallen muss. Üblicherweise überträgt sich eine solche Fehlaufstellung um eine
Größenordnung verstärkt auf die Lage des Strahls. Besitzt ein Quadrupolmagnet eine
Fehlaufstellung in Bezug auf seine Sollposition, hat er neben seiner fokussierenden Wirkung auf den Teilchenstrahl die ablenkende Wirkung eines Dipolmagneten. Diese stört
die Teilchenbahn und muss mit Dipolkorrektoren kompensiert werden.
Langfristig sollten allerdings die Fehlaufstellungen korrigiert werden. Dazu ist eine
geodätische Vermessung mit anschließender Positionskorrektur üblicherweise die Methode der Wahl. Da diese Methode aber nur im abgeschalteten Zustand des Beschleunigers
anwendbar ist, werden Positionsänderungen von Komponenten - etwa durch thermische
Belastungen - während des Betriebs mit Strahl nicht erfasst. Zur Messung und Korrektur der Fehlaufstellungen der Quadrupole werden bei DELTA strahlbasierte Methoden
eingesetzt. Diese nutzen Lageinformationen des Strahls, die aus der Auslese von Strahllagemonitoren (BPMs) gewonnen werden, um die Fehlaufstellungen der beteiligten Komponenten zu ermitteln. Im Rahmen der vorliegenden Arbeit werden zwei voneinander
unabhängige strahlbasierte Methoden eingehend betrachtet und angewendet. Eine der
Methoden ist dabei von einer theoretischen Beschreibung der Teilchenoptik im Ring unabhängig und wurde bei DELTA erstmalig angewendet.
In Kapitel 2 werden zunächst theoretische Grundlagen behandelt. Dabei werden die zur
Strahlführung nötigen Magnettypen vorgestellt und die Teilchenbahn durch eine ideale
Magnetstruktur beschrieben. Anschließend werden Störungen der idealen Teilchenbewegung diskutiert. In Kapitel 3 wird die Magnetstruktur des DELTA Speicherrings und die
in dieser Arbeit verwendeten Diagnose- und Korrektursysteme vorgestellt.
Die beiden angewendeten strahlbasierten Methoden werden im Folgenden eingehend
besprochen und hinsichtlich ihrer Eigenschaften im Vergleich bewertet. Es folgen die
Ergebnisse der Messungen mit den unterschiedlichen Methoden an ausgewählten Quadrupolstrukturen und die Ergebnisse der Korrektur der Fehlaufstellung. Die Arbeit endet
mit einer Zusammenfassung und einem kurzen Ausblick.
3
2. Grundlagen der Strahloptik
In diesem Kapitel werden die Grundlagen für das Verständnis der strahlbasierten Messmethoden vorgestellt. Zunächst wird dabei auf die Kräfte, die auf einen geladenen Teilchenstrahl wirken, eingegangen. Dann werden die zur Strahlführung nötigen Magnettypen
vorgestellt und die Teilchenbewegung in einer idealen Magnetstruktur beschrieben. Zum
Schluss werden Störungen der idealen Teilchenbewegung und Hystereseeffekte diskutiert.
Dieses Kapitel folgt in großen Teilen der Argumentation von [29, 30].
2.1. Beschleunigung und Ablenkung
Um die Bewegung eines geladenen Teilchens zu beeinflussen, muss eine Kraft auf dieses
wirken. Von den vier prinzipiell zur Verfügung stehenden Kräften der Natur (Gravitation,
Elektromagnetismus, starke und schwache Kraft), bleibt nur die elektromagnetische Kraft
übrig, da alle anderen Kräfte entweder zu schwach sind oder ihre Reichweite zu kurz
ist. Bewegt sich ein geladenes Teichen der Ladung q und Geschwindigkeit ~v durch ein
elektromagnetisches Feld, so wirkt auf dieses die Lorentzkraft
~ + E).
~
F~ = q(~v × B
(2.1)
Da diese Arbeit an einem Elektronenbeschleuniger durchgeführt wurde, werden im Folgenden nur Elektronen betrachtet, es gilt also q = −e, wobei e die Elementarladung ist.
Magnetfelder sind nicht geeignet geladene Teilchen zu beschleunigen, da der magnetische
Term der Lorentzkraft nach (2.1) immer senkrecht zur Bewegungsrichtung wirkt. Magnetfelder lenken ein bewegtes geladenes Teilchens daher nur ab. Der elektrische Term
der Lorentzkraft (2.1) wirkt auf ein geladenes Teilchen immer in Richtung des elektrischen Feldes. Es ist damit in der Lage geladenen Teilchen zu beschleunigen, wenn das
Feld eine Komponente in der Bewegungsrichtung des Teilchens besitzt. Dieses erfährt
daher den Energiegewinn ∆E mit
Z~r1
∆E = −e
~ r = −eU
Ed~
(2.2)
~
r0
wobei U die durchlaufene Potentialdifferenz auf dem Weg von ~r0 nach ~r1 ist.
5
Kapitel 2. Grundlagen der Strahloptik
Bei Elektronenbeschleunigern hat man es in der Regel mit hochrelativistischen Teilchen
zu tun, für die v ≈ c gilt. Möchte man auf ein solches Teilchen eine Kraft transversal
~ und B-Feld
~
zur Bewegungsrichtung ausüben, so haben E-,
die gleiche Wirkung, wenn
|E| = c|B| ist (vgl. (2.1)). Mit normalleitenden Magneten sind Felder bis zu B ≈ 1,5 T
realisierbar1 . Eine äquivalente Wirkung lässt sich mit einem elektrischen Feld der Stärke
E ≈ 450 · 106
V
m
erzielen. In Vakuum realisierbar2 sind aber nur Felder bis E = 40 · 106
V
m
[19, 6], während mit supraleitenden Magneten sogar magnetische Felder bis B ≥ 8 T möglich sind. Dies entspricht der Wirkung eines elektrischen Feldes der Stärke E ≥ 2,4·109
V
m.
Aus diesem Grund verwendet man überwiegend Magnetfelder um hochenergetische geladene Teilchenstrahlen entlang eines vorgegebenen Pfades zu führen.
2.2. Koordinatensystem
In der Regel ist die transversale Strahlbreite sehr klein gegenüber den Abmessungen des
gesamten Beschleunigers. Zur Beschreibung der Dynamik der einzelnen Teilchen im Strahl
wäre also ein Koordinatensystem ungeeignet, dessen Ursprung fest mit dem Beschleuniger verbunden ist. Man definiert daher eine ideale Referenzteilchenbahn, den „Sollorbit“.
Dieser beschreibt genau die Bahn, der ein Referenzteilchen mit Sollenergie folgen würde.
Sie ist durch die Magnetstruktur des Beschleunigers festgelegt. Weiter definiert man ein
Koordinatensystem Σ(s,x,y), dessen Ursprung sich mit der Geschwindigkeit des Referenzteilchens auf dem Sollorbit mitbewegt, siehe Abb. 2.1. Die s-Koordinate beschreibt
die longitudinale, die x- und y-Koordinate die transversale Position eines beliebigen Teilchens in Bezug auf das Referenzteilchen. Dieses Koordinatensystem ermöglicht es, die
Teilchenbewegung in unmittelbarer Nähe um den Sollorbit zu beschreiben.
2.3. Strahlführung
2.3.1. Magnetfelder
Bewegt sich ein geladenes Teilchen durch ein Magnetfeld B(s,x,y), so erfährt es die
Lorentzkraft und wird transversal von seiner Bahn abgelenkt. Aus dem Kräftegleichgewicht zwischen Zentrifugal3 - und Lorentzkraft
F~Zentrifugal + F~Lorentz = 0
1
2
3
Mit Eisenmagneten sind Felder bis B ≈ 2 T möglich, aber ab B ≈ 1 T setzt die Sättigung ein. Technisch
nutzbar sind Felder bis B ≈ 1,5 T
Oberhalb der Durchschlagsspannung kommt es durch Feldemission zu Überschlägen, die die aufgebaute
Spannung schlagartig entladen.
~Zentrifugal = pv , dabei ist p der Impuls, v die Geschwindigkeit des Teilchens und R
Zentrifugalkraft: F
R
der Krümmungsradius der Teilchenbahn
6
(2.3)
2.3. Strahlführung
y
eTeilchenbahn
s
Sollorbit
x
Abbildung 2.1.: Koordinatensystem Σ(s,x,y) das mit dem Referenzteilchen mitbewegt
wird [30].
folgt für den Krümmungsradius R(s,x,y) der Bahn
e
1
= B(s,x,y)
R(s,x,y)
p
(2.4)
wobei e die Ladung eines Elektrons und p der relativistische Impuls des Teilchens sind.
Die direkte Umgebung der Strahlachse wird als frei von Ladungsträgern und Strömen
angenommen. Die Wechselwirkung der Strahlteilchen untereinander ist ein Effekt höherer
Ordnung und soll an dieser Stelle vernachlässigt werden. Das magnetische Feld, das
auf die Strahlteilchen wirkt, kann dann aus einem Potential V (s,x,y) abgeleitet werden.
Dieses muss eine Lösung der ladungsfreien Laplace-Gleichung
∆V = 0
(2.5)
sein. Nimmt man an es würden keine longitudinalen Felder existieren, so erfüllt der
Ansatz [29]
V (r,ϕ,s) = −
pX 1
An (s)rn einϕ
e
n!
(2.6)
n≥0
mit den komplexen Koeffizienten An (s), die Laplace-Gleichung in Zylinder-Koordinaten (r,ϕ,s). Das Magnetfeld ergibt sich dann als Gradient des Potentials. Real-, und
Imaginärteil des Ansatzes sind unabhängige Lösungen der Laplace-Gleichung. Die Potentialentwicklung bis zur 3. Ordnung sieht dann in kartesischen Koordinaten wie folgt
aus [29]
e
− V (s,x,y)
p
=
1
A1 [x + iy] + A2 i(x2 − y 2 ) + xy . . .
2
1 3
1
2
2
3
+A3 i(x − 3xy ) + (3x y − y ) + . . .
6
6
(2.7)
7
Kapitel 2. Grundlagen der Strahloptik
Speicherringe werden in der Regel in der horizontalen Ebene aufgebaut. Zur Ablenkung
und Fokussierung eines Teilchenstrahls werden in einem solchen Speicherring hauptsächlich Magnete verwendet, deren Potential durch den Realteil der Entwicklung beschreiben
werden. Im Folgenden soll daher nur der Realteil der Entwicklung betrachtet werden.
Aus der Lösung der Laplace-Gleichung leitet sich dann die folgende Multipol-Zerlegung
des Magnetfeldes ab
~
~
B(s,x,y)
= −∇(Re(V
(s,x,y)))
(2.8)
Für die vertikale Komponente des Magnetfeld ergibt sich damit [29]
e
By (s,x,y)
p
=
e
A1 (s)
p
+
e
A2 (s)x
p
+
e
1
A3 (s) (x2 − y 2 )
p
2
+
...
=
1
R(s)
+
k(s)x
+
1
m(s)(x2 − y 2 )
2
+
...
(2.9)
und für die horizontale Komponente [29]
e
Bx (s,x,y)
p
=
0
+
e
A2 (s)x
p
+
e
A3 (s)xy
p
+
...
k(s)x
+
m(s)xy
+
...
(2.10)
=
Dabei sind
1
R
= pe A1 , k = pe A2 und m = pe A3 die energieinvarianten Multipol-Stärken.
2.3.2. Elemente der Strahlführung
Dipole
Zur Ablenkung eines geladenen Teilchenstrahls wird die niedrigste Multipolkomponente
n = 1 des Magnetfeldes verwendet. Diese entspricht dem Feld eines magnetischen Dipols.
Die Feldstärke ist dabei unabhängig von der (x,y)-Position, somit ist der Krümmungsradius R der Bahn bezüglich (x,y) konstant und nur noch von s abhängig. Ein solches Feld
wird von zwei planparallelen Äquipotentialflächen erzeugt (vgl. Abb. 2.2). Alle Dipole
zusammen lenken den Strahl in einem Speicherring um 360 ◦ ab.
Quadrupole
Der Teilchenstrahl wird in einem Speicherring über einen langen Zeitraum gespeichert.
Dabei kommt es aufgrund verschiedener Effekte zu einer Divergenz des Strahls. Um diese
zu kompensieren, müssen die Teilchen des Strahls auf die Sollbahn fokussiert werden. Die
8
2.3. Strahlführung
y
1
Eisenjoch
Spule
0.5
-1
e-
x
-0.5
0.5
1
-0.5
-1
Abbildung 2.2.: Links: Äquipotential-Flächen, die ein Dipolfeld erzeugen. Rechts: Querschnitt eines Dipolmagneten ausgeführt als „C-Magnet“. [30]
Multipolkomponente n = 2 erzeugt ein linear mit der Ablage von der Sollbahn anwachsendes Feld. Die Feldverteilung entspricht der eines magnetischen Quadrupols. Dieser
fokussiert den Strahl je nach Polarität nur in einer Ebene und defokussiert ind der anderen. Durch eine geeignete Kombination von Quadrupolen alternierender Polarität lässt
sich jedoch insgesamt eine fokussierende Wirkung in beiden Ebene realisieren („alternierende Gradientenfokussierung“). Die Anwesenheit von Quadrupolfeldern führt dazu, dass
der Teilchenstrahl quasiharmonische Schwingungen um die Strahlachse ausführt (siehe
Kap. 2.4.3). Die Dynamik eines geladenen Teilchenstrahls in Dipol- und Quadrupolfel-
z
z
Spulen
Eisenjoch
S
N
x
N
S
hyperbolische
Polflächen
Abbildung 2.3.: Querschnitt durch einen Quadrupolmagneten [30].
dern wird von der linearen Strahloptik beschrieben.
9
Kapitel 2. Grundlagen der Strahloptik
Sextupole
Ein realer Teilchenstrahl ist nie monochromatisch. Die Teilchen besitzen eine Energieverteilung um eine Sollenergie. Teilchen mit Energie- und Impulsabweichung werden in den
Quadrupolen zu schwach oder zu stark fokussiert (vgl. (2.10)). Diesen Effekt nennt man
z
Spulen
Eisenjoch
N
S
S
x
N
N
S
Abbildung 2.4.: Querschnitt durch einen Sextupolmagneten [30].
Chromatizität. Da Teilchen mit zu großem oder zu kleinem Impuls auch in den Dipolen
unterschiedlich abgelenkt werden, gelangen diese Teilchen auf eine Dispersionsbahn. Sextupole lassen sich in Kombination mit der Dispersionsbahn nutzen die Chromatizität zu
kompensieren. Da die Sextupole allerdings ein nichtlineares Feld erzeugen, verlässt man
mit ihrem Einbau in einen Beschleuniger den Bereich der linearen Strahloptik.
Dipolkorrektoren
Durch unvermeidbare Dipolstörfelder wird der Strahl vom Sollorbit abgelenkt. Um den
Strahl zurück auf den Sollorbit zu zwingen werden Dipolkorrektoren verwendet. Bei zu
vielen oder zu starken Dipolstörfeldern ist eine Strahlführung ohne Korrektur überhaupt
nicht möglich. Gelegentlich möchte man in Beschleunigern den Teilchenstrahl gezielt
vom Sollorbit ablenken und lokal eine Bahn mit bestimmter Ablage und/oder Winkel
erzeugen. Auch dazu verwendet man Dipolkorrektoren. Durch eine Linearkombination
mehrerer Dipolkorrektoren lässt sich lokal eine geschlossene Beule um den Sollorbit herum
erzeugen, die den Orbit außerhalb dieser Beule nicht beeinflusst.
2.4. Bewegung entlang des Sollorbits
Zur Beschreibung der Bewegung der Teilchen entlang des Sollorbits wird zunächst die
Bewegungsgleichung für beide Ebenen aufgestellt. Dazu soll im Folgenden ein ebener
Beschleuniger betrachtet werden, in dem nur horizontale Ablenkmagnete existieren.
10
2.4. Bewegung entlang des Sollorbits
2.4.1. Bewegungsgleichung
Die Teilchenbewegung wird im zuvor definierten mitbewegten Koordinatensystem Σ(s,x,y)
beschrieben. Durch eine Transformation der Teilchenbewegung aus dem Laborsystem in
das Koordinatensystem des Sollteilchens erhält man die folgenden linearen Bewegungsgleichungen
d2
x(s) +
ds2
1
1 ∆p
− k(s) x(s) =
2
R (s)
R(s) p0
2
d
y(s) + k(s)y(s) = 0
ds2
(2.11)
(2.12)
Dabei wurde nur die Multipolentwicklung (2.9)-(2.10) bis zur 2. Ordnung beachtet, die
relative Impulsabweichung der Strahlteilchen als klein angenommen ( ∆p
p 1) und Produkte und Potenzen von x, y und
∆p
p0
vernachlässigt, da x R, y R,
Der von den Dipolen stammende Term
1
R2 (s)
∆p
p0
1.
führt zu einer horizontalen Fokussierung,
die im Gegensatz zur starken Fokussierung der Quadrupole −k(s) als „schwache Fokussierung“ bezeichnet wird. Die Bewegungsgleichungen sind in Dipolen und Quadrupolen
nicht gekoppelt. Betrachtet man nur Teilchen mit Sollimpuls
ke und schwache Fokussierung zu κ(s) =
1
R(s)2
∆p
p0
= 0 und fasst star-
− k(s) zusammen, so vereinfacht sich
die horizontale Bewegungsgleichung (2.11) zur einer Differentialgleichung des „Hillschen
Typs“
d2
x(s) + κ(s)x(s) = 0.
ds2
(2.13)
Eine analoge Differentialgleichung erhält man für die y-Ebene.
2.4.2. Lösung der Bewegungsgleichung für Einzelteilchen
Eine allgemeine Lösung der Hillschen Differentialgleichung für beliebige Magnetfelder ist
nicht möglich. Wenn man den longitudinalen Verlauf der Magnetfelder allerdings durch
ein „Rechteckmodell“ in dem der Magnetfeldverlauf stückweise konstant ist κ(s) = κ (vgl.
Abb. 2.5) nähert, wird stückweise eine analytische Lösung möglich. Um die Wirkung
auf den Teilchenstrahl korrekt wiederzugeben, muss die Länge der Magnete durch eine
„effektive Länge“
Z
leff =
B(s)
ds
B0
(2.14)
ersetzt werden. Mit der Näherung des Rechteckmodells vereinfacht sich die Hillsche Differentialgleichung zu einer Differentialgleichung 2. Ordnung mit konstanten Koeffizienten.
d2
x(s) + κx(s) = 0
ds2
(2.15)
11
Kapitel 2. Grundlagen der Strahloptik
B
realer
Feldverlauf
RechteckModell
B0
l eff
s
Abbildung 2.5.: Schematisch dargestellter Verlauf des realen Magnetfeldes und des
durch das Rechteckmodell approximierten Feldes in Abhängigkeit der longitudinalen Position s. Der Bereich des approximierten Feldverlaufs hat die Länge leff und wird effektive
Magnetlänge genannt.
Die Lösung dieser lautet
√
√
x(s) = A cosh κs + B sinh κs
√
√
√
√
x0 (s) =
κA sinh κs + κB cosh κs
(2.16)
(2.17)
mit den Anfangsbedingungen x(0) = x0 und x0 (0) = x00 folgt
√
√
1
x(s) = x0 cosh κs + x00 √ sinh κs
κ
√
√
√
0
0
x (s) = x0 κ sinh κs + x0 cosh κs
(2.18)
(2.19)
Mit (2.18) und (2.19) lässt sich die Teilchenbewegung abschnittsweise durch Teile der
Magnetstruktur mit konstantem κ verfolgen. Dabei sind die Anfangsbedingungen x0 und
x00 für jedes Teilchen verschieden. Dies führt dazu, dass jedes Teilchen eine andere Bahn
verfolgt. Die Einhüllende der Schar aller Einzelteilchenbahnen ist die „Enveloppe“, siehe
Abb. 2.6.
Die Trajektorie des Ladungsschwerpunkts in der zweidimensionalen transversalen Ebene geht nach einem vollständigen Umlauf in sich selbst über. Diese spezielle geschlossene
Teilchenbahn wird „Closed-Orbit“ genannt.
Dünne Magnete
Der Krümmungsradius R der Teilchenbahnen ist in den Magneten in der Regel sehr viel
größer als die longitudinale Ausdehnung der Magnete. Die Magnete lassen sich daher als
12
2.4. Bewegung entlang des Sollorbits
x
s
Teilchenbahn
Enveloppe
x
s
Abbildung 2.6.: Enveloppe und Einzelteilchenbahnen [30].
dünne Elemente betrachten und verursachen in dieser Näherung nur eine Winkeländerung
der Bahn. Für den Krümmungsradius der Bahn im Rechteckmodell gilt
e
1
= B(x,y)
R
p
(2.20)
Der dünne Magnet lenkt den Strahl somit um den Winkel
Zleff
Θ=
e
e
B(x,y)ds = B(x,y)leff
p
p
(2.21)
0
ab. Für einen Dipol folgt mit B(x,y) aus (2.10)
ΘD =
1
· leff
R
(2.22)
und analog für einen Quadrupol
ΘQ = k · x · leff
(2.23)
ein Quadrupol wird so analog zur geometrischen Optik durch eine „dünne Linse“ beschrieben.
13
Kapitel 2. Grundlagen der Strahloptik
2.4.3. Betatronschwingung
Die Einzelteilchenlösung der Hillschen Differentialgleichung aus Kap. 2.4.2 beschreibt
nicht das kollektive Verhalten des Gesamtstrahls. Die Differentialgleichung soll daher
noch einmal für den gesamten Strahl gelöst werden. Die Lösung x(s) von (2.13) stellt
eine Schwingung der Teilchen um den Sollorbit dar, die Betatronschwingung genannt
wird. Amplitude und Phase sind dabei ortsabhängig. (2.13) lässt sich durch
p
x(s) = β(s) cos(ϕ(s) − ϕ0 )
(2.24)
mit den Integrationskonstanten und ϕ0 lösen. wird Emittanz und die ortsabhängige
Amplitudenfunktion β(s) Betafunktion genannt. Für die ortsabhängige Phase ergibt sich
aus (2.24)
Zs
ϕ(s) =
dσ
.
β(σ)
(2.25)
0
ϕ(s) beschreibt die Phase des Gesamtstrahls und wird Betatronphase genannt, während
die Integrationskonstante ϕ0 eine beliebige Anfangsphase der Einzelteilchen zwischen 0
und 2π beschreibt. Die Differenz der Betatronphase zwischen zwei verschiedenen Orten
s wird auch Phasenvorschub genannt. Mit dem Phasenvorschub über einen vollständigen
Umlauf ϕ(L) definiert man den Arbeitspunkt ν als
1
ϕ(L)
=
ν=
2π
2π
ZL
ds
β(s)
(2.26)
0
Der Arbeitspunkt gibt die Anzahl ν der Betatronschwingungen um den Sollorbit bei
einem vollständigen Umlauf an.
2.5. Störungen
2.5.1. Dipolstörungen
Durch Dipolfeldfehler entstehen Störungen des Closed-Orbit. Diese können etwa durch
Feldfehler der Dipolmagnete entstehen, d.h. durch zu starke oder zu schwache Dipolmagnete. Eine Verdrehung von horizontal ablenkenden Dipolmagneten um die longitudinale
Achse führt dazu dass ein Teil der Bewegung in die vertikale Ebene eingekoppelt wird
und so störend wirkt. Eine weitere nicht zu vernachlässigende Quelle von Dipolstörungen
sind transversale Fehlaufstellungen von Magneten höherer Multipolordnung. Tritt ein
störendes Dipolfeld am Ort si auf, das den Strahl um den Winkel ΘDi ablenkt, so wird
die Änderung des Closed-Orbit am Ort s durch
p
β(s)β(si )
uco (s) =
ΘDi cos(νπ − νϕ(s) + νϕ(si ))
2 sin πν
14
(2.27)
2.6. Hysterese
beschrieben [29]. Treten an mehreren Orten si Dipolstörungen auf, so werden diese superponiert
uco (s) =
X
i
Anhand des
1
sin πν -Terms
p
β(s)β(si )
ΘDi cos(νπ − νϕ(s) + νϕ(si ))
2 sin πν
(2.28)
in (2.28) erkennt man die Bedeutung des Arbeitspunktes ν aus
(2.26). Nimmt dieser einen ganzzahligen Wert an, so divergiert die Closed-Orbit-Störung
und führt zu einem Verlust des Teilchenstrahls.
2.5.2. Quadrupolstörungen
Als Quadrupolstörung bezeichnet man zusätzliche ungewollte Quadrupolfelder. Diese
können z.B. durch Fertigungsfehler oder falsche Bestromung der Quadrupolmagnete entstehen. Tritt an den Orten s eine Störung der Quadrupolstärke k(s) um den Betrag ∆k(s)
auf, so verschieben diese den Arbeitspunkt ν um
1
∆ν =
4π
I
∆k(s)β(s)ds
(2.29)
für ∆k(s) k(s). Damit wird durch Quadrupolfeldfehler die Fokussierung des Beschleunigers geändert. Die daraus resultierende Änderung der Betafunktion am Ort s für kleine
Störungen ∆k lässt sich durch
∆β(s) = −
β(s)
2 sin 2πν
I
β(s0 )∆k(s0 ) cos 2(ϕ(s0 ) − ϕ(s)) − 2πν ds0
(2.30)
ausdrücken[30]. Man sieht sofort, dass der Ausdruck für ganz- und halbzahlige Werte von
ν aufgrund des
1
sin 2πν -Terms
divergiert. Durch das Anwachsen der Betafunktion wächst
auch die Strahlbreite, was zu einem Verlust des Teilchenstrahls führt.
2.6. Hysterese
Der Großteil der Magnete, die bei DELTA zum Einsatz kommen, sind konventionelle
Eisenmagnete. Die magnetischen Momente des Magneteisens sind innerhalb der Weißschen Bezirke gleich ausgerichtet. Im unmagnetisierten Zustand unterscheiden sich die
Weißschen Bezirke untereinander aber in ihrer Ausrichtung, so dass die gesamte mittlere
Magnetisierung des Materials Null ist.
~ hier durch Bestromen der
Bringt man ein Eisenjoch in das äußeres Magnetfeld H,
um das Eisenjoch gewickelten Spulen, so richten sich die Weißschen Bezirke im Material
entlang des äußeren Feldes aus und erzeugen so eine makroskopische Magnetisierung. Die
15
Kapitel 2. Grundlagen der Strahloptik
Sättigung
Magnetisierung M
Remanenz
Grenzkurve
Neukurve
Koerzitivfeldstärke
Sättigung
H-Feld
~ als Funktion des äußeren Magnetfeldes H.
~ Die
Abbildung 2.7.: Magnetisierung M
~
dargestellte Hysteresiskurve der Magnetisierung entsteht, wenn das äußere Magnetfeld H
~ max , dann monoton fallend bis auf
von 0 monoton steigend bis auf einen Maximalwert H
~ max und wieder zurück variiert wird. [11]
−H
~ (H)
~ des Materials erzeugte magnetische Flussdichte4 B
~ im
durch die Magnetisierung M
Material
~ = µ0 (H
~ +M
~ (H))
~
B
mit
~ (H)
~ = (µr − 1)H
~
M
(2.31)
~
~ = µ0 H,
~ da für Eisen
ist viel stärker die nur durch das H-Feld
erzeugte Flussdichte B
µr ≈ 5500 beträgt. Die Magnetisierung des Materials steigt zunächst linear mit dem
~ erreicht aber einen Sättigungswert M
~ s , wenn alle Weißschen Beäußeren Magnetfeld H,
~
zirke entlang des äußeren Magnetfeldes ausgerichtet sind. Die magnetische Flussdichte B
~ der Spulen an.
im Material steigt dann nur noch linear mit magnetischen Feldstärke H
Schaltet man das äußere Magnetfeld ab, so verbleibt ein Teil der Weißschen Bezirke in
seiner Orientierung. Es bleibt eine Restmagnetisierung, die Remanenz, zurück. Diese verschwindet erst nach Anlegen eines äußeren Gegenfeldes, der Koerzitivfeldstärke. Erhöht
~ s der Magnetisierung.
man das Gegenfeld weiter, so erreicht man den Sättigungswert −M
~ (H),
~
Beim Durchfahren des äußeren Magnetfeldes durchläuft man die Hysteresiskurve M
siehe Abb. 2.7. Für die Eisenmagnete in Teilchenbeschleunigern bedeutet dies, dass nach
einer Erhöhung und darauf folgender Absenkung der Bestromung auf den Ursprungswert das von ihm erzeugt Magnetfeld nicht die gleiche Stärke hat wie vorher. Bei den in
4
~ entsprechend dem üblichen
In den restlichen Kapiteln dieser Arbeit wird die magnetische Flussdichte B
~ als Magnetfeld bezeichnet.
Sprachgebrauch anstelle von H
16
2.6. Hysterese
den folgenden Kapiteln vorgestellten Messmethoden wird aber eine Variation der Quadrupolfeldstärke benötigt. Dabei ist allerdings nur der Betrag der Feldstärkenänderung
von Bedeutung. Da bei jeder Änderung der Feldstärke die Hysteresiskurve durchlaufen
wird, sollte die Feldstärke zuerst abgesenkt und anschließend um den gleichen Betrag
wieder angehoben werden, da es so möglich ist nach Abschluss der Variation wieder den
Magnetisierung
Ausgangspunkt in der Hysteresiskurve zu erreichen (vgl. Abb. 2.8) [11].
3
4
2
5
1
6
Setzwert
H-Feld
~
Abbildung 2.8.: Ausschnitt der Hysteresiskurve M ( ~H.
) und zwei mögliche Pfade, die zu
~ |-Änderung führen [11]. Erreicht man die |∆M
~ |-Änderung indem man
der gleichen |∆M
~ von (1) nach (2) bewegt, so ist es durch
sich durch eine Erhöhung des Magnetfeldes H
~ auf den ursprünglichen Wert nicht möglich den Ausgangspunkt (1)
ein Absenken von H
auf der Kurve zu erreichen. Statt dessen erreicht man den Punkt (3). Erzeugt man die
~ |-Änderung jedoch durch eine Absenkung des Magnetfeldes H
~ von (1) nach (6), so
|∆M
~ wieder den Ausgangspunkt (1)
erreicht man durch ein anschließendes Anheben von H
[11].
17
3. DELTA
In diesem Kapitel wird zunächst die bestehende Magnetstruktur des Speicherrings beschrieben. Dabei wird auf die Diagnose- und Korrektursysteme eingegangen, die für die
Messungen in den folgenden Kapiteln verwendet wurden. Der erste Teil des Kapitels basiert auf vorangegangenen Arbeiten an DELTA1 . Zum Abschluss werden thermische und
mechanische Einflüsse auf die Position der Quadrupolmagnete diskutiert und Messungen
zum thermischen Verhalten vorgestellt.
3.1. Magnetstruktur
DELTA ist ein Synchrotron mit einem Umfang von 115,2 m, das als Speicherring betrieben wird. Der gespeicherte Elektronenstrahl besitzt eine Maximalenergie von 1,5 GeV.
Typischerweise werden für den Nutzerbetrieb 130 mA Strahlstrom akkumuliert. Das Ziel
beim Design von DELTA war es kleine Emittanzen zu erreichen und Platz für sogenannte „Insertion-Devices“ 2 zu bieten. Dazu wurde DELTA in vier Quadranten aufgeteilt, die
jeweils spiegelsymmetrisch zueinander ausgebaut sind. Die Bögen im Osten und Westen bestehen aus einer Abfolge von Triplett-Zellen, siehe Kap. 3.1.1. Im Norden und
Süden befinden sich zwischen den Bögen gerade Sektionen, die Platz für je drei „Insertion Devices“ bieten, die durch 3 ◦ - bzw. 7 ◦ -Ablenkmagnete voneinander getrennt sind.
Zwischen den Bögen und den Geraden befinden sich „Dispersion-Suppressor-Zellen“, die
die Dispersion in den Geraden zu Null kompensieren. Die im Synchrotron „BoDo“ 3 beschleunigten Elektronen werden über einen Transferkanal mit gepulsten Magneten in der
Mitte des östlichen Bogens in DELTA injiziert. Um den Energieverlust der Elektronen
durch Abstrahlung von Synchrotronstrahlung auszugleichen befindet sich in der Mitte
des westlichen Bogens ein 500 MHz Cavity. In der nördlichen Geraden ist der Undulator
U250 installiert, der dem Betrieb eines „Free-Electron-Lasers“ dient. In der südlichen Ge1
2
Als Quellen sind hier zu nennen: [2, 7, 8, 9, 10, 12, 21, 24].
Insertion Device: Überbegriff für verschiedenartige Magnetstrukturen, die die Strahllage im restlichen
Beschleuniger nicht beeinflusse dürfen. Insertion Devices sind z.B. Undulatoren/Wiggler, die zur
3
Erzeugung von Synchrotron-Strahlung genutzt werden.
BoDo ist ein Akronym für „Boostersynchrotron Dortmund.
19
Kapitel 3. DELTA
raden befindet sich der Undulator U55 und ein supraleitender asymmetrischer Wiggler
[22], kurz SAW.
3.1.1. Triplettstruktur
Ein einzelner Quadrupol wirkt immer nur in einer Ebene fokussierend und in der anderen
defokussierend. Um insgesamt eine Fokussierung in beiden Ebene zu erreichen, kommen
Triplettzellen zum Einsatz. Die Struktur der Tripettzelle im ursprünglichen Design und
der Verlauf der optischen Funktionen in einer solchen sind in Abb. 3.1 dargestellt. Zwei
Abbildung 3.1.: Aufbau der Triplettzellen im ursprünglichen Design und Verlauf der
optischen Funktionen [21].
benachbarte Triplettzellen bilden jeweils eine Struktur von drei Quadrupolen zwischen
zwei langen Dipolen aus. Davon wirken zwei Quadrupole horizontal defokussierend und
einer horizontal fokussierend. Der horizontal fokussierende Quadrupol (kurz QF) hat die
doppelte Länge der defokussierenden Quadrupolen (kurz QD) und befindet sich mittig
zwischen ihnen [21]. Im Folgenden wird mit Quadrupoltriplett immer die Struktur QDQF-QD bezeichnet.
20
3.1. Magnetstruktur
3.1.2. Magnettypen
Dipole
Dipole entsprechen, gemäß den Ausführungen in Kap. 2.3.1, der niedrigsten Ordnung
der Multipolentwicklung des Magnetfeldes und bewirken eine Ablenkung des Elektronenstrahls. Sie sind bei DELTA als Rechteckmagnete ausgeführt und haben einen C-förmigen
Querschnitt (vgl. Abb. 2.2 und Abb. 3.2). Dadurch kommt es zu zusätzlicher Kantenfokussierung, da der Teilchenstrahl nicht senkrecht in die Stirnseite des Dipols eintritt.
Die Magnetjoche kommen in zwei verschiedenen Ausführungen vor. Die langen Dipole
Abbildung 3.2.: Aufbau eines kurzen DELTA-Dipolmagneten. links: Ansicht von oben.
rechts: Ansicht Strahlaustrittsseite [2].
lenken den Strahl um 20◦ ab und haben eine Länge von 1,15 m. Die kurzen Dipole lenken
den Strahl je nach Bestromung um 7◦ oder 3◦ ab und haben eine Länge von 0,52 m.
Die Spulenwindungen sind aus Kupferrohr gefertigt, durch welches zur Kühlung Wasser
fließt.
Quadrupole
In den Triplettzellen der Bögen kommen zur Fokussierung des Strahls zwei verschiedene Quadrupoltypen zum Einsatz. Die kurzen defokussierenden Quadrupole haben eine
Länge von 0,2 m, die fokussierenden Quadrupole haben eine Länge von 0,4 m. Alle Quadrupole sind mit wassergekühlten Kupferspulen bestückt. Insgesamt existieren in DELTA
76 Quadrupole, von denen jeweils zwei oder vier zusammen in einer von insgesamt 24
Gruppen (Familien) von jeweils einem Netzgerät bestromt werden. Die Netzgeräte sind
in der Lage die Quadrupole mit maximal ±60 A zu bestromen. Ab einer Bestromung mit
40 A kommen Sättigungseffekte des Magneteisens zum Tragen.
21
Kapitel 3. DELTA
Abbildung 3.3.: Aufbau eines kurzen DELTA-Quadrupolmagneten [2]. links: Ansicht
qn04+02
qn03+0
qn 02 + 2
qn01+002
2
qd
qf0 04+
q d 3 + 05
0 4 03
+0
6
qn06+02
qn05+02
qn08+01
qn07+01
qn04+01
qn06+01
qn05+01
1
qn03+0 1
qn02+0 1
qn01+0
4
+0
04 02
qd f03+ 03
q 0 4+
qd
q
q d0
qd f03 4+
04 +0 02
+0 1
1
qd0
3
qf02 +01
qd0 +01
2 +0
1
qn08+02
qn07+02
Strahlaustrittsseite. rechts: Ansicht von oben.
7
+0 4
04 +0 08
d
q f03 4+
q d0
q
2
3 +0
q d 0 2 +0 2
0
f
q
2
2+0
qd0
qd01+02
qd01+01
qf01+01
qf01+02
qd01+04
qd01+03
qs08+02
qs09+02
qd
q 04 +
qd f03+ 14
04 0 7
+1
3
qs01+0
qs02+0 2
qs03+0 2
2
qs04+02
qs05+02
qs06+02
qs07+02
qs08+01
qs09+01
1
+1
04 0 6
qd 3+ 12
qf0 04+
qd
1
qs01++001
qs02 1
qs03+0
qs04+01
qs05+01
qs06+01
qs07+01
qd
qf002+03
qd0 2+03
3+0
3
q
q d0
qd f03 4+
0
+
04 0 9
+1 5
0
4
2+0
qd0 +04
2
0
q f 0 3+0 4
qd
6
+1 8
04 3+0 15
d
q f0 4+
q d0
q
Abbildung 3.4.: Position und Nomenklatur der Quadrupol-Magnete im DELTASpeicherring [11].
22
3.1. Magnetstruktur
Sextupole
Zur Korrektur der Chromatizität, siehe Kap. 2.3.2, sind bei DELTA zusätzliche Sextupolmagnete installiert. Diese sind als externe und interne Sextupole ausgeführt.
Das Eisenjoch der externen Sextupole ist über nichtmagnetische Träger aus Aluminum
an den Eisenjochen der Quadrupole montiert. Insgesamt wurden bei DELTA 54 externe
Sextupole installiert. Zusätzlich zu den externen Sextupolen gibt es noch interne Sextu-
Abbildung 3.5.: Aufbau der DELTA-Sextupol-Magnete [2]. links: Externer SextupolMagnet. rechts: Interner Sextupol-Magnet.
pole. Diese nutzen zum einen das Joch und die vier Polschuhe der Quadrupole und zum
anderen jeweils zwei zusätzliche Polschuhe, die in den Quadrupolen ober- und unterhalb
der Vakuumkammer zwischen den Quadrupol-Polschuhen installiert wurden, wie in Abb.
3.5 skizziert ist. Das Windungsverhältnis von Polschuhspulen zu Jochspulen ist so abgestimmt, dass die Dipolkomponente des erzeugten Feldes verschwindet [2, 7]. Insgesamt
wurden bei DELTA 28 interne Sextupole installiert. Davon befinden sich 18 in den langen
Quadrupolen und 10 in den kurzen.
Dipolkorrektoren
Um den Orbit gezielt verändern oder korrigieren zu können wurden bei DELTA 30 horizontale (Nomenklatur: hk01-hk30) und 26 vertikale (vk01-vk26) Dipolkorrektoren an den
in Abb. 3.6 skizzierten Positionen installiert. Des Weiteren existieren fünf weitere DCSpulen dc1-dc5, die der Strahllagevariation im Injektionsbereich dienen. Mit Ausnahme
der DC-Spulen sind alle Dipolkorrektoren durch Zusatzspulen auf den Quadrupoljochen
realisiert, wie in Abb. 3.7 skizziert. Gemäß (2.27) skaliert die Wirkung einer Dipolstörung
mit der β-Funktion am Ort der Störung. Die Korrektoren sind folglich am Ort maximaler
β-Funktion am effektivsten. Daher sind die horizontalen Korrektorspulen in den horizontal fokussierenden Quadrupolen und die vertikalen Korrektorspulen entsprechend in den
23
13
hk
hk12
vk10
hk11
hk10
vk09
vk07
hk08
hk06
hk07
vk06
hk05
vk05
04
hk
v
hk k04
03
vk08
hk09
Kapitel 3. DELTA
11
vk k1 4
h
2 dc1
vk1
5
hk113
vk
dc2
vk
hk003
2
vk0
2
vk01
hk16
hk01
dc3
vk14
d c4
vk1
h k1 5
7
vk1
6 dc5
vk21
hk24
hk26
vk22
hk25
vk23
hk27
19
vk18
h k2 0
hk21
vk19
hk22
vk20
hk23
hk
h
vk k 1 8
17
hk
29
hk k24
v
28
6
vk2
0
3
k
h 25
vk
Abbildung 3.6.: Position der Dipolkorrektoren im Speicherring. Mit Ausnahme der
DC-Spulen dc1-dc5 sind alle Korrektoren als Zusatzspulen auf kurzen oder langen Quadrupolen realisiert [11].
Abbildung 3.7.: Die auf den Quadrupolen installierten Dipol-Korrektor-Spulen (blau)
erzeugen einen Feldverlauf wie durch die Pfeile skizziert. [7] links: horizontaler Korrektor.
rechts: vertikaler Korrektor.
24
3.1. Magnetstruktur
vertikal fokussierenden Quadrupolen installiert, da dort die β-Funktion der jeweiligen
Ebene maximal ist (vgl. Abb. 3.1).
Da die Korrektorspulen das Eisenjoch der Quadrupole verwenden, erzeugen sie kein
reines Dipolfeld. Feldstärkemessungen ergaben, dass die durch die Korrektoren erzeugten
Sextupolkomponenten vergleichbar mit den Sextupolfeldern der internen Sextupole ist
[7, 2].
Die Korrektorspulen werden jeweils von einem unipolaren4 , stromgeregelten Netzgerät
mit Polwender5 bestromt. Dieses wird von einem 12 Bit DAC6 gesteuert, der Setzwerte
zwischen 0 A und 10 A zulässt. Der vom Netzgerät ausgegebene Strom kann über einen
12 Bit ADC7 zurückgelesen werden. Da 1 Bit für das Vorzeichen des Stroms benötigt
wird, resultiert aus der 12 Bit Auflösung des DAC bzw. ADC eine Genauigkeit von Setzund Rücklesewert von 10 A/211 ≈ 4,8 mA.
4
5
unipolar: Es kann zwar die Stärke des Gleichstroms verändert werden, aber nicht die Stromrichtung.
Da die Stromrichtung der unipolaren Netzgeräte nicht geändert werden kann, muss mechanisch die
Polarität des Anschlusses der Korrektorspulen getauscht werden um einen Wechsel der Stromrichtung
zu bewirken.
DAC (engl.): digital to analog converter
7
ADC (engl.): analog to digital converter
6
25
Kapitel 3. DELTA
3.2. Diagnose- und Korrektursysteme
3.2.1. Strahllagemonitore
Zur Überwachung der Strahlposition in der Magnetstruktur werden Strahllagemonitore,
kurz BPMs8 , eingesetzt. Diese sind bei DELTA in die Vakuumkammer integriert. Die
Vakuumkammer wurde dazu an den Stellen verstärkt, an denen Strahllagemonitore installiert werden sollten, so dass sie dort den in Abb. 3.8 dargestellten Monitorkopf ausbildet. In einen Monitorkopf sind an der Ober- und Unterseite der Vakuumkammer je zwei
kapazitive Pickup-Elektroden eingelassen. Passiert der Elektronenstrahl den Monitor-
Koaxial-Verbinder
(SMA-Stecker)
Keramik-Isolation
Pickup-Elektrode
1
10.80 mm
20 mm
2
z
x
37 mm
29.8 mm
3
4
Abbildung 3.8.: DELTA Strahllagemonitorkopf. Dargestellt ist die verstärkte Vakuumkammer in die die 4 Pickup-Elektroden zur Strahllagemessung eingelassen wurden [8].
kopf, so verursacht er in den Pickup-Elektroden eine Ladungsverschiebung, abhängig von
Strahlstrom, Strahlposition und transversaler Ladungsverteilung [3, 8]. Aus den Spannungssignalen ui der Elektroden i = 1 . . . 4 lässt sich über
x = ax
(u2 + u4 ) − (u1 + u3 )
u1 + u2 + u3 + u4
(3.1)
y = ay
(u1 + u2 ) − (u3 + u4 )
u1 + u2 + u3 + u4
(3.2)
und
8
BPM (engl.): beam position monitor
26
m2
1
m2
2
bp
b p m2 0
bp
bpm18
bpm19
bpm16
bpm17
bpm14
05
bpm13
bpm12
bpm11
bpm
04
m
bpm10
b p m0 9
bp
m
8
m0
bp 07
m
bp
bp
bpm15
3.2. Diagnose- und Korrektursysteme
06
23
m
b p m2 4
bp
25
bpm
26
bpm
bpm
03
bpm27
bpm02
bpm01
bpm28
bpm29
bpm54
bpm
30
bpm
31
53
bpm
52
bpm
bpm43
bpm42
bpm45
bpm44
bpm47
bpm46
bp
m
bp 49
m4
8
bpm36
bpm37
bpm38
bpm39
bpm40
bpm41
4
m3
bp 35
m
bp
bp
b p m3 2
m
33
51
m
bp m50
bp
Abbildung 3.9.: Positionen im DELTA-Speicherring, an denen Strahllagemonitore in
der Vakuumkammer installiert wurden [12].
die transversale Strahlposition ermitteln. Dabei sind ax und ay monitorabhängige Kalibrierungsfaktoren, die in der Nähe des Symmetriepunktes des Monitors in guter Näherung als konstant angenommen werden können [8]. Zur Auswertung der Signale der
Pickup-Elektroden werden Messelektroniken der Firma BERGOZ [17] Precision-BeamInstrumentation verwendet. An einigen Strahllagemonitoren kommen LIBERA [14] Elektroniken der Firma i-tech zum Einsatz.
Die Strahllage kann mit den Strahllagemonitoren in Bezug auf die mechanische Mitte des Monitorkopfes mit einer Genauigkeit von ±200 µm bestimmt werden. Eine relative Änderung der Strahllage kann mit einer Genauigkeit von ±5 µm bestimmt werden [8]. Konstruktionsbedingt können sich die fixierten Strahllagemonitore maximal um
±70 µm gegenüber dem Quadrupol in dem sie montiert sind bewegen. Die nicht fixierten Strahllagemonitore in DELTA haben allerdings einen größeren Bewegungsspielraum
von ±(1,8 bis 2,0) mm im Quadrupol. Aus diesem Grund müssen insbesondere die nichtfixierten Strahllagemonitore auf die Achsen der benachbarten Quadrupole kalibriert werden. Dazu wird bei DELTA die in Kap. 4.1 vorgestellte strahlbasierte Messmethode
verwendet.
Insgesamt sind in DELTA an 54 Positionen, die in Abb. 3.9 dargestellt sind, Monitorköpfe in der Vakuumkammer installiert.
27
Kapitel 3. DELTA
3.2.2. Orbitkorrektur und Sollorbit
Der Designorbit beschreibt den Orbit, der in der idealen Magnetstruktur, die keine Aufstellungsfehler besitzt, durch die Zentren der Quadrupole verläuft. Wie zuvor beschrieben, bestehen die Bögen des DELTA Speicherrings aus Triplettzellen, von denen zwei
benachbarte jeweils eine Struktur von Quadrupolstripletts ausbilden. An den äußeren
Quadrupolen der Tripletts ist jeweils ein Strahllagemonitor installiert. Die Quadrupole
können sich in Folge von thermischen Effekten bewegen und können daher Aufstellungsfehler bezüglich ihrer Designpositionen besitzen. Die Strahllagemonitore werden durch
eine strahlbasierte Messmethode, siehe dazu Kap. 4.1, auf die magnetischen Mitten der
jeweiligen Quadrupole kalibriert. Aus diesem Grund liefern sie keine Informationen über
die Strahllage in Bezug auf den Designorbit.
Der Sollorbit in DELTA ist daher der Orbit, der durch die Nullpositionen der Strahllagemonitore definiert wird und verläuft somit durch die Mitten der Quadrupole, die mit
einem solchen Strahllagemonitor ausgestattet sind. Die Orbitkorrektur kann den Elektronenstrahl mit Hilfe der Dipolkorrektoren dorthin führen.
Um die Strahllage zu korrigieren bzw. gezielt zu verändern wird bei DELTA eine Orbitkorrektursoftware eingesetzt [7], die die Dipolkorrektoren steuert.
Lenkt man den Strahl mit dem Dipolkorrektor i um den Winkel Θi ab und zeichnet
die Strahllageänderung ∆xj (bzw. ∆yj ) an den n Strahllagemonitoren von DELTA auf,
−→
so erhält man einen n-dimensionalen Vektor ∆x = (∆x1 , . . . ,∆xn ). Dieser Vektor wird
nach einer Normierung auf den Ablenkwinkel Responsevektor ~ri genannt.
~ri =
−→
∆x
Θi
(3.3)
Zeichnet man die Responsevektoren ri für alle m Dipolkorrektoren auf, erhält man eine
n × m-dimensionale Responsematrix
R(~r1 . . . ~rm )
(3.4)
deren Spalten die m Responsevektoren enthalten. Bildet man die Inverse der Response−−→
matrix R und multipliziert diese mit dem m-dimensionalen Vektor ∆O der gewünschten
Orbitänderung,
−→
−−→
∆k = R−1 ∆O
(3.5)
−→
so erhält man einen n-dim Vektor ∆k, der die Änderung der Ablenkwinkel der n Korrektoren enthält, die nötig sind um die gewünschte Orbitänderung zu erzeugen. Da bei
Beschleunigern in der Regel die Zahl m der Strahllagemonitore nicht mit der Zahl n der
Korrektoren übereinstimmt, ist die Responsematrix R in der Regel nicht quadratisch.
28
3.2. Diagnose- und Korrektursysteme
Daher wird von der Software das SVD9 -Verfahren [7] verwendet um für nichtquadratische Responsematrizen eine Pseudoinverse zu bestimmen. Die Software liest die Daten
der Strahllagemonitore (Orbit) aus und bestimmt die Abweichung des gemessenen Orbits
von der gewünschten Orbit-Referenz. Mit dem SVD-Verfahren werden dann die nötigen
Stärken der Dipolkorrektoren ermittelt, um die Orbitabweichung zu kompensieren.
3.2.3. Relais-Kaskade
Die 76 DELTA-Quadrupole werden in Familien, von jeweils 2 oder 4 Magneten, jeweils
in Reihe von einem von 30 Netzgeräten bestromt. Daher kann ihre Bestromung nicht
individuell unabhängig voneinander verändert werden. Für die im Folgenden vorgestellten Messmethoden ist eine individuelle Variation der Quadrupolbestromung allerdings
notwendig.
Um eine individuelle Variation einzelner Quadrupolstärken zu ermöglichen wurden zwei
zusätzliche Netzgeräte installiert. Diese Geräte können parallel zu einem der Quadrupole über eine kaskadierende Relaisschaltung geschaltet werden [9] und versorgen diesen
dann individuell mit einem Zusatzstrom, der seine Stärke gezielt verändert. Ein positiver Zusatzstrom führt auf einem horizontal fokussierenden Quadrupol zu einer stärkeren
horizontalen Fokussierung [12].
3.2.4. Kontrollsystem
Die Steuerung der Relaiskaskade und der meisten übrigen Komponenten des Beschleunigers geschieht über das Kontrollsystem. Das DELTA-Kontrollsystem basiert auf EPICS
[16]. Alle wichtigen Variablen und Messgrößen haben in der EPICS Datenbank eigene
Einträge, die Records heißen. Diese können ausgelesen oder verändert werden. Verschiedene EPICS-Records können in einem EPICS-Log protokolliert werden. So ist eine spätere
Auswertung des zeitlichen Verhaltens der einzelnen Einträge möglich. Die Steuerung der
Magnetströme und die Auslese der Daten der Strahllagemonitore geschieht ebenfalls über
EPICS-Records. Magnetströme die über die Records ausgelesen werden, können mit dem
Programm i2k [7] in die jeweiligen Multipolstärken der DELTA-Magnete umgerechnet
werden. In die andere Richtung wird das Programm k2i verwendet um Multipolstärken
in die zur Erzeugung nötigen Stromstärken umzurechnen. MATLAB [15] ist über die Erweiterung labca [26] in der Lage auf die EPICS-Records zuzugreifen und die Parameter
zu ändern.
9
SVD (engl.): singular value decomposition [20]
29
Kapitel 3. DELTA
3.2.5. Induktive Wegaufnehmer
Zur Überwachung und Protokollierung der Bewegung verschiedener mechanischer Komponenten, insbesondere der Vakuumkammer, der Strahllagemonitorköpfe und der Quadrupole werden bei DELTA induktive Wegaufnehmer des Typs IW 15A/5-0.25-S-R der
Firma TWK-ELEKTRONIK eingesetzt [10, 24]. Ein solcher ist in Abb. 3.10 abgebildet. Die
Signalspannung der Wegaufnehmer kann über EPICS-Records abgerufen bzw. protokolliert werden. Die wichtigsten technischen Daten wurden dem technischen Datenblatt [18]
entnommen und in Tab. 3.1 aufgeführt.
Messhub
=
5 mm (10 V)
Genauigkeit (rel.)
=
±0,25 %
Genauigkeit (abs.)
≤
±12,5 µm
Temperaturdrift
≤
±0,008 %
Restwelligkeit
<
5 mVss
max. Messfrequenz
≤
100 Hz
Tabelle 3.1.: Die wichtigsten technische Daten der induktiven Wegaufnehmer des Typs
IW 15A/5-0.25-S-R der Firma TWK-ELEKTRONIK [18].
Abbildung 3.10.: Induktiver Wegaufnehmer des Typs IW 15A/5-0.25-S-R der Firma
TWK-ELEKTRONIK [18].
Die Wegaufnehmer basieren auf dem Funktionsprinzip einer Differentialdrossel. Der
Tastkopf ist am Ende einer nichtmagnetische Stange befestigt. Am anderen Ende befindet
sich ein magnetischer Kern. Dieser befindet sich in Ruhestellung des Wegaufnehmers
mittig zwischen zwei identischen Spulen, deren Induktivitäten somit gleich sind. Bewegt
sich der magnetische Kern durch eine Bewegung des Tastkopfes aus der Mitte heraus, so
sind die Induktivitäten der beiden Spulen nicht mehr gleich. Über eine Brückenschaltung
kann die Induktivitätsdifferenz in eine Spannungsdifferenz transformiert werden. Diese
ist dann proportional zur Position des Tastkopfes.
Die Stange mit dem Tastkopf wird von einer Metall-Feder aus dem Gehäuse gedrückt.
Ist sie maximal ausgefahren, so gibt der Wegaufnehmer eine Signalspannung von 0 V aus.
30
3.3. Thermische und mechanische Einflüsse auf die Quadrupole
Je weiter die Stange in das Gehäuse gedrückt wird, desto größer wird die Signalspannung,
bis sie bei 5 mm Eindringtiefe einen Maximalwert von 10 V erreicht. Die zugehörigen
EPICS-Records wurden so angelegt, dass eine Signalspannung von 5 V der Nullposition
0 mm entspricht, so sind also positive und negative Positionswerte möglich.
3.3. Thermische und mechanische Einflüsse auf die
Quadrupole
Die in dieser Arbeit diskutierten Messverfahren beziehen sich ausschließlich auf die Quadrupolmagnete. Daher sollen hier nur thermische Effekte diskutiert werden, die auf die
Quadrupolmagnete wirken. Da DELTA 5 Tage pro Woche in Betrieb ist und zwei Tage stillsteht, kühlen in den zwei Tagen Stillstand (Shutdown) alle Komponenten auf die
Hallentemperatur ab. Nach dem Einschalten erwärmen sich die Komponenten nach einigen Stunden bis Tagen Betrieb wieder und erreichen erst dann ihre Betriebstemperatur
[24, 25].
3.3.1. Thermische Ausdehnung der Quadrupole
Die kurzen Quadrupole werden in der Regel mit ca. 30 A bestromt, die langen mit ca.
50 A. Trotz Wasserkühlung erwärmen sich die Stromleitungen stark und heizen damit
das gesamte Quadrupoljoch auf. In Abb. 3.12 sind Wärmekamerabilder dargestellt, die
einen kurzen und einen langen Quadrupol unter Betriebsbedingungen zeigen.
Abbildung 3.11.: Realansicht eines Quadrupols zur Verdeutlichung des für die Aufnahme der Thermobilder gewählten Bildausschnitts
31
Kapitel 3. DELTA
Abbildung 3.12.: Wärmekamerabilder des in Abb. 3.11 dargestellten Bildausschnitts
zweier Quadrupole10 unter Betriebsbedingungen. Die angezeigte Temperatur gibt die Temperatur der mit dem mittigen Fadenkreuz markierten Stelle wieder. oberes Bild: kurzer
Quadrupol bei einer Bestromung mit 31 A. unteres Bild: langer Quadrupol bei einer Bestromung mit 51 A.
32
3.3. Thermische und mechanische Einflüsse auf die Quadrupole
Den Wärmekamerabildern ist zu entnehmen, dass die Magnettemperatur bei einer Bestromung mit 31 A bzw. 51 A von der Umgebungstemperatur von ca. 21 ◦ C auf 28 ◦ C
bzw. 38 ◦ C steigt. Das entspricht einem Temperaturanstieg um 7 ◦ C bzw. 17 ◦ C. Die aus
„1200-100A“-Stahl [2] gefertigten Quadrupoljoche besitzen einen linearen Ausdehnungskoeffizienten α ≈ 10 · 10−6 K−1 . Die Quadrupole haben eine transversale Ausdehnung
von l0 = 798 mm. Der Temperaturanstieg ∆T durch die Bestromung führt zur einer
Erhöhung ∆l der transversalen Ausdehnung, welche gemäß
∆l = l0 α∆T
(3.6)
∆l = (55 − 135) µm
(3.7)
zu
abgeschätzt werden kann. Da die horizontale Lagerung der Quadrupole symmetrisch ist
(vgl. Abb. B.1), führt die Ausdehnung des Quadrupols zu keiner horizontalen Verschiebung seiner magnetischen Mitte.
3.3.2. Translation der Quadrupole
Thermische Bewegung der Vakuumkammer
Die DELTA-Vakuumkammer ist aus nichtmagnetischem Stahl gefertigt und wird einseitig
auf der Außenseite wassergekühlt. Sie besteht aus Einzelelementen, die bis zu 10 m lang
sind. Beim Einschalten nach dem wöchentlichen Shutdown wird zunächst ohne Strahlbetrieb die Wasserkühlung eingeschaltet. Da die Kühlwassertemperatur bei kaltem Maschinenzustand niedriger als die Hallentemperatur sein kann, wird die Vakuumkammer
einseitig auf der Außenseite abgekühlt und zieht sich zunächst nur dort zusammen, da
es etwa 4 Stunden dauert bis die Vakuumkammer, aufgrund der schlechten Wärmeleitfähigkeit des Materials, eine gleichmäßige Temperatur erreicht hat [25]. Die einseitige
Abkühlung führt zu einer Verkrümmung der Vakuumkammer nach außen. Nach einiger
Betriebszeit steigt die Kühlwassertemperatur an und damit auch die Temperatur der
Außenseite der Vakuumkammer. Bei Strahlbetrieb wird die Außenseite der Vakuumkammer zusätzlich durch die vom Elektronenstrahl emittierte Synchrotronstrahlung abhängig
vom Strahlstrom, der in der Regel zwischen 70 mA bis 130 mA liegt, erwärmt [24], sie
befindet sich also kontinuierlich in thermischer Bewegung. Da sich die Vakuumkammer
häufig in direktem Kontakt zu den Quadrupolen oder Sextupolen befindet, die an diesen
montiert sind, werden diese durch die Bewegung der Vakuumkammer mitbewegt. Dies
resultiert in einer transversalen Fehlaufstellung der Quadrupole und führt zu störenden
Dipolfeldern (vgl. Kap. 2.5.1).
10
kurzer Quadrupol: qd04+11, langer Quadrupol: qf03+06
33
Kapitel 3. DELTA
Schwingungen der Trägerstruktur
Die Dipole und Quadrupole sind fest auf einer Trägerstruktur aus Stahl montiert. Diese
schwingt unter anderem durch den Betrieb der Vakuumpumpen und Kühlaggregaten im
Bereich von 5 Hz bis 73 Hz mit einem Maximum bei 5 Hz bei einer maximalen Amplitude
von 1 µm [28]. Diese Schwingungen übertragen sich auf die Quadrupole und können
über einen gewissen Zeitraum hinweg dazu führen, dass sich die Magnete von ihren
Sollpositionen weg bewegen, was wiederum zu störenden Dipol-Feldern führt.
3.3.3. Messung der thermischen Ausdehnung und Verschiebung der
Quadrupole
Um die im voran gegangenen Kapitel gemachten Überlegungen quantitativ zu überprüfen, wurde der in Abb. 3.13 dargestellte Messaufbau verwendet. Dazu wurden zwei der in
Kap. 3.2.5 beschriebenen Wegaufnehmer jeweils auf einer stabilen Messsäule aus Aluminium montiert und so platziert, dass ihre Tastköpfe mittig an die Innen-, und Außenseite
eines Quadrupols angreifen. Der Tastkopf des Wegaufnehmers, der an die Innenseite angreift, musste dazu mit einer ca. 40 cm langen Aluminiumstange verlängert werden, da
es aufgrund der Wasser- und Strom-Zuleitungen des Quadrupols nicht möglich war die
Messsäule mit dem Wegaufnehmer nah genug an dem Quadrupol zu platzieren. Die Füße
der Messsäulen wurden zusätzlich mit Gewichten bestückt um die Gefahr des Verrutschens zu vermindern. Dieser Messaufbau ist dazu geeignet die thermische Ausdehnung
Quadrupol
Wegaufnehmer (innen)
Aluminum-Säule
Wegaufnehmer (außen)
Aluminum-Säule
Abbildung 3.13.: Aufbau zur Messung der thermische Ausdehnung von Quadrupolen
34
3.3. Thermische und mechanische Einflüsse auf die Quadrupole
und eine transversale Verschiebung zu detektieren und zu quantifizieren, sofern sich der
Quadrupol im thermischen Gleichgewicht befindet.
In den Abbildungen 3.14-3.15 ist das Ergebnis einer solchen Messung für einen langen Quadrupol (qf03+06 ), der sich im östlichen Bogen von DELTA befindet, graphisch
dargestellt. Die dargestellte Messung wurde während des Einschaltens von DELTA durchgeführt. Es ist zu beobachten, dass beide Tastköpfe im Mittel eine Bewegung nach außen
-1.2
-1.25
-1.3
-1.35
-1.4
-1.45
Wegaufnehmerpos ition [mm]
(innen)
Wegaufnehmerpos ition [mm]
(aus s en)
detektieren. Dies entspricht einer Ausdehnung des Quadrupols.
-1.5
07:50
08:50
09:50
10:50
11:50
12:50
13:50
14:50
Datum / Uhrzeit
15:50
16:50
17:50
18:50
19:50
08:50
09:50
10:50
11:50
12:50
13:50
14:50
Datum / Uhrzeit
15:50
16:50
17:50
18:50
19:50
1.78
1.76
1.74
1.72
1.7
1.68
1.66
07:50
Abbildung 3.14.: Thermisches Verhalten eines langen Quadrupols qf03+06 beim Einschalten. oben: Wegaufnehmer auf der Außenseite des Quadrupols unten: Wegaufnehmer
auf der Innenseite.
Die Kontraktion des Quadrupols im Zeitraum 07:50 - 08:45 Uhr ist durch die StandardEinschaltprozedur zu erklären. Diese sieht zuerst das Einschalten der Wasserkühlung vor.
In diesem Fall führte dies zu der beobachteten Kontraktion des Quadrupols, da die Hallentemperatur und damit auch die Temperatur des Quadrupols über der des Kühlwassers
lag und das Quadrupoljoch somit zunächst abgekühlt wurde. Danach wurden die Quadrupole bestromt, in diesem Fall mit 51.21 A, was zu einer Erwärmung des Quadrupoljoches
auf 38 ◦ C führt, vgl. Abb. 3.12. Infolge dessen dehnt sich der Quadrupol über einen Zeitraum von mehreren Stunden aus. Der Ausdehnung überlagert ist eine Verschiebung des
Quadrupols. Nach 8-10 Stunden befindet sich der Quadrupol im thermisches Gleichgewicht. Wie Abb. 3.14 zu entnehmen ist, hat der Wegaufnehmer auf der Innenseite dabei
eine Positionsänderung des Tastkopfes von ∆xinnen = (−80 ± 18) µm aufgezeichnet, der
auf der Außenseite zeichnete eine Positionsänderung von ∆xaußen = (+170 ± 18) µm auf.
35
-1.38
-1.39
-1.4
-1.41
-1.42
-1.43
-1.44
07:55
Wegaufnehmerpos ition [mm]
(innen)
Wegaufnehmerpos ition [mm]
(aus s en)
Kapitel 3. DELTA
08:00
08:05
08:10
08:15
08:20
08:25 08:30 08:35
Datum / Uhrzeit
08:40
08:45
08:50
08:55
09:00
08:00
08:05
08:10
08:15
08:20
08:25 08:30 08:35
Datum / Uhrzeit
08:40
08:45
08:50
08:55
09:00
1.78
1.76
1.74
1.72
1.7
1.68
1.66
07:55
Abbildung 3.15.: Kontraktion und anschließende Verschiebung eines langen Quadrupols durch Einschalten der Wasserkühlung (vergrößerter Ausschnitt aus Abb. 3.14).
Die Messungenauigkeit resultiert aus dem Messfehler der induktiven Wegaufnehmer. Der
lange Quadrupol hat sich also um
∆llang = ∆xinnen + ∆xaußen = (90 ± 25) µm
(3.8)
ausgedehnt. Der gemessene Wert liegt in der gleichen Größenordnung, wie die in (3.7)
gemachte Abschätzung. Gleichzeitig hat sich das Zentrum des Quadrupols gemäß11
1
∆xShift = −∆xinnen + ∆l
2
(3.9)
aufgrund der thermischen Bewegung der Vakuumkammer um xShift = (125±22) µm nach
außen verschoben.
3.3.4. Aufstellungsfehler der Quadrupole
Im Oktober 2005 wurde bei DELTA eine vollständige Vermessung der Magnetpositionen durchgeführt [11, 23]. Diese mit geodätischen Methoden durchgeführte Vermessung
basiert auf optischer Triangulation spezieller Positionsmarker, die auf den Magneten angebracht sind. Die Genauigkeit des verwendeten Verfahrens ermöglicht eine Bestimmung
der absoluten Magnetpositionen auf 100 µm bis 200 µm. Als Ergebnis dieser Vermessung ist zu bemerken, dass die horizontalen Quadrupolpositionen zum Teil stark von
11
Das negative Vorzeichen vor ∆xinnen rührt aus der Konvention, dass der Wegaufnehmer auf der Innenseite bei einer Quadrupolbewegung nach außen eine abfallende Signalspannung ausgibt.
36
3.3. Thermische und mechanische Einflüsse auf die Quadrupole
ihren Designpositionen abweichen. Die Abweichungen schwanken zwischen −3,0 mm und
+4,5 mm.
Diese starken Fehlaufstellungen führen dazu, dass ein Strahlbetrieb in DELTA ohne
die Dipolkorrektoren nicht möglich ist. Dadurch werden die Dipolkorrektoren allein zur
Führung des Strahls entlang des Sollorbits stark belastet. Für verschiedene Experimente
sind an den jeweiligen Insertion-Devices bestimmte Orbitbeulen nötig. Dies belastet die
Dipolkorrektoren weiter. Die Korrektorstärken zur Einstellung eines Standard-NutzerOrbits12 sind in Abb. 3.16 graphisch dargestellt. Einige der Korrektoren sind durch diese
K orrektors trom I [A]
10
5
0
-5
-10
1
2
3
4
5
6
7
8
6
7
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Nummer des horizontalen K orrektors
K orrektors trom I [A]
10
5
0
-5
-10
1
2
3
4
5
8
9
10 11 12 13 14 15 16 17 18 19 20 21
Nummer des vertikalen K orrektors
22 23 24 25 26
Abbildung 3.16.: Bestromung der einzelnen Dipolkorrektoren zur Einstellung eines
Standard-Nutzer-Orbit.
beiden Ursachen stark bzw. maximal belastet (I = 10 A). Dies führt dazu, dass sie die
geforderten Ablenkwinkel nicht erzeugen können. Zum Teil sind Dipolkorrektoren stark
belastet, während die benachbarten Dipolkorrektoren schwach oder gar nicht belastet
sind, siehe z.B. „vk04“ und „hk08“ in Abb. 3.16. Ist eine solche Konfiguration der Korrektorstärken zu beobachten, ist dies ein Indiz für eine Quadrupolfehlaufstellung, siehe
dazu Kap. 6.4.2.
Eine Korrektur der Quadrupolfehlaufstellungen ist daher für den stabilen Betrieb des
Speicherrings unbedingt erforderlich. Dazu geeignete Methoden werden im folgenden Kapitel vorgestellt.
12
Nutzer-Orbit: Sollorbit, der für die Experimente nötige Orbit-Beulen enthält
37
4. Strahlbasierte Messmethoden
In diesem Kapitel werden die in dieser Arbeit angewendeten strahlbasierten Messmethoden vorgestellt. Da für alle strahlbasierten Messmethoden eine genaue Kenntnis der
Strahllage erforderlich ist, müssen zunächst die Strahllagemonitore kalibriert werden.
Die dafür bei DELTA verwendete strahlbasierte Messmethode [8, 9], wird im Abschnitt
4.1 vorgestellt. Darauf folgend werden zwei strahlbasierte Messmethoden präsentiert, die
es ermöglichen die Fehlaufstellung eines Triplettquadrupols in Bezug auf die Achse der
beiden anderen Triplettquadrupole zu bestimmen.
4.1. Bestimmung von Offsets der Strahllagemonitore
Für alle strahlbasierten Messmethoden ist eine genaue Kenntnis der Elektronenstrahlposition im gesamten Speicherring grundlegend. Diese Informationen werden von den
Strahllagemonitoren geliefert. Diese messen die Strahllage zunächst aber nur in Bezug
auf ihre eigene Position. Durch thermische Effekte können sich die nicht fixierten Strahllagemonitore allerdings gegenüber ihren zugehörigen Quadrupolen bewegen (vgl. Kap.
3.3.2). Diese Positionsänderung verursacht dann einen Offset bei der Bestimmung der
Strahlposition. Es ist daher nötig die Strahllagemonitore auf die magnetische Achse der
benachbarten Quadrupole kalibrieren zu können. Zur Bestimmung der Offsets wird bei
DELTA ein strahlbasiertes Verfahren verwendet [8, 9].
4.1.1. Strahlbasierte Methode
Messprinzip
Passiert ein Elektronenstrahl einen Quadrupol mit Ortsablage x, so wird er von diesem
nach (2.23) um den Winkel
Θ = leff · k · x
(4.1)
abgelenkt. In der Mitte des Quadrupols, also bei Ablage (x,y) = (0,0) verschwindet das
Feld und der Strahl erfährt keine Ablenkung. Hat der Strahl eine Ablage (x,y), die von
Null verschieden ist, ändert sich bei einer Variation der Quadrupolstärke von k auf k+∆k
39
Kapitel 4. Strahlbasierte Messmethoden
der Ablenkwinkel Θ des Quadrupols. Dadurch entsteht ein neuer Closed-Orbit, der auch
die Ablage x im Quadrupol selbst um ∆x ändert. Für ∆k k gilt ∆x x und damit
∆Θ = leff · ∆k · x
(4.2)
Diese Änderung des Ablenkwinkels führt nach (2.27) zu einer Änderung des Closed-Orbits
p
β(s)β(si )
∆Θ cos(νπ − νϕ(s) + νϕ(si ))
(4.3)
uco (s) =
2 sin πν
Diese Closed-Orbit-Änderung kann mit den Strahllagemonitoren aufgezeichnet werden
und ist proportional zur Ablage x des Strahls in Bezug auf die Quadrupolachse und der
Änderung der Quadrupolstärke ∆k.
Abbildung 4.1.: Strahlbasierte Kalibration der Strahllagemonitore. Dargestellt sind die
gemessenen Werte der mittleren quadratischen Ablage (Abweichungsquadrat) für unterschiedliche Strahlablagen im Strahllagemonitor und die angepasste Parabel.
Mit mindestens drei Dipolkorrektoren kann eine Orbitbeule mit definierter Ablage erzeugt werden. So ist es möglich den Strahl mit verschiedenen Ablagen durch den Strahllagemonitor zu führen. Der Designabstand der Strahllagemonitor zum anliegenden Quadrupol beträgt nur 17 cm, daher hat der Strahl im Quadrupol näherungsweise die gleiche Ablage wie im Strahllagemonitor. Für verschiedene Ablagen x im Strahllagemonitor
wird nun die Quadrupolstärke von k auf k + ∆k angehoben und die daraus resultierende
40
4.1. Bestimmung von Offsets der Strahllagemonitore
Closed-Orbit-Änderung an allem Strahllagemonitoren im Speicherring aufgezeichnet. Die
Closed-Orbit-Änderung ist minimal bzw. Null, wenn der Strahl durch die magnetische
Mitte des Quadrupols verläuft. Aus der aufgezeichneten Closed-Orbit-Änderung wird das
Abweichungsquadrat
∆x2 =
1
NBPM
·
NX
BPM
(∆xi )2
(4.4)
i=1
berechnet, dabei ist NBPM die Anzahl der verwendeten Strahllagemonitore und ∆xi die
Closed-Orbit-Änderung am Strahllagemonitor i.
Das Abweichungsquadrat ist bei konstantem ∆k proportional zum Quadrat der Ablage
x im Strahllagemonitor [9] (siehe Abb. 4.1)
∆x2 ∝ x2
(4.5)
An die gemessenen Werte der Abweichungsquadrate für die verschiedenen Ablagen x wird
nun eine Parabel
p(x) = ax (x − xoff )2 + c
(4.6)
angepasst. Der Wert xoff beschreibt die Position des Minimums und gibt den gesuchten
Offset des Strahllagemonitors in Bezug auf die Quadrupolmitte an.
Eine Messung der Closed-Orbit-Änderung mit konstantem ∆k für Orbitbeulen mit
verschiedener Ablage ermöglicht somit eine Bestimmung der Lage des Nullpunktes des
Strahllagemonitors in Bezug auf die magnetische Achse des benachbarten Quadrupols.
41
Kapitel 4. Strahlbasierte Messmethoden
4.2. Bestimmung von Quadrupolfehlaufstellungen
Im Folgenden werden zwei strahlbasierte Messmethoden vorgestellt, mit denen es möglich
ist, die Fehlaufstellung eines Triplettquadrupols zu bestimmen. Die Positionen der horizontal defokussierenden Quadrupole der Tripletts definieren den Sollorbit, da diese mit
Strahllagemonitoren ausgestattet sind, die auf die magnetische Achse des jeweils benachbarten Quadrupols kalibriert sind. Somit kann nur der mittlere horizontal fokussierende
Quadrupol eines Tripletts eine Fehlaufstellung in Bezug auf diesen Sollorbit besitzen. Seine Fehlaufstellung bezieht sich daher auf die Achse, die durch die magnetischen Mitten
der äußeren beiden Quadrupole definiert wird.
4.2.1. Modellbasierte Methode
Diese Methode basiert auf der Variation der Quadrupolstärke ∆k des mittleren fokussierenden Triplettquadrupols. Die dadurch entstehende Orbit-Änderung („Orbit-Antwort“)
wird in einem MATLAB-basierten Optik-Modell mit der Accelerator Toolbox1 simuliert.
Aus den Simulationsdaten lassen sich Rückschlüsse auf die Fehlaufstellung des mittleren
Triplettquadrupols ziehen. Die Methode wurde vor Beginn dieser Arbeit entwickelt und
an DELTA angewendet [13, 12] und soll in diesem Kapitel kurz beschrieben werden.
Im Folgenden wird nur die horizontale Ebene betrachtet, da in dieser bei DELTA die
größten Fehlaufstellungen auftreten. In der horizontalen Ebene hat der mittlere Triplettquadrupol eine fokussierende und die äußeren Quadrupole eine defokussierende Wirkung.
Prinzipiell kann die Methode auch in der vertikalen Ebene angewendet werden [13, 12].
Messprinzip
Der gespeicherte Elektronenstrahl wird für die Messung so geführt, dass er genau durch
die magnetischen Mitten der beiden äußeren Quadrupole des zu vermessenden Tripletts
verläuft. Besitzt der mittlere Triplettquadrupol eine Fehlaufstellung, so kann der Strahl
das Triplett nicht gradlinig passieren. Der Strahl muss in diesem Fall unter einem Winkel
in das Triplett ein- und austreten. Er beschreibt somit einen wie in Abb. 4.2 skizzierten
Verlauf, der abhängig von der Fehlaufstellung des mittleren fokussierenden Quadrupols
ist. Alle Magnete werden als dünne Elemente betrachtet (vgl. Kap. 2.4.2). Im mittleren
Quadrupol hat der Strahl in Bezug auf die Triplettachse die Ablage xg und in Bezug auf
seine magnetische Mitte die Ablage xc mit
xc = xg − xoff
1
Die Accelerator Toolbox [27] ist Teil des Matlab Middle Layer Pakets.
42
(4.7)
4.2. Bestimmung von Quadrupolfehlaufstellungen
θ+Δθ
BPM
BPM
Δxc
θ
xg
xc
xoff
s12
Sollorbit
s23
QF
QD
QD
Abbildung 4.2.: Schematische Darstellung des Verlaufs des Elektronenstrahls in einem Quadrupol-Triplett, bestehend aus zwei defokussierenden Quadrupolen und einem
fokussierenden Quadrupole, bei einer Fehlaufstellung xoff des mittleren, fokussierenden
Quadrupols. Die durchgezogene Linie skizziert die Elektronenbahn ohne zusätzliche Quadrupolstärke ∆k, die gestrichelte Linie skizziert die Elektronenbahn mit ∆k.
Er wird von dem Quadrupol, gemäß (2.23) um den Winkel
Θ = xc · k · leff
(4.8)
abgelenkt.
Ändert man die Stärke k des mittleren Quadrupols minimal um ∆k k so ändert
sich der Ablenkwinkel des Quadrupols. Ein neuer Closed-Orbit stellt sich ein, der im
mittleren Quadrupol die Ablage xc + ∆xc hat. Mit der Änderung der Ablage xc um ∆xc
und des k-Werts um ∆k folgt aus (4.8)
Θ + ∆Θ = (xc + ∆xc )(k + ∆k) · leff
(4.9)
Subtrahiert man (4.8) von (4.9) so erhält man eine Gleichung für die Änderung des
Ablenkwinkels ∆Θ
∆Θ = (xc ∆k + ∆xc k + ∆xc ∆k) · leff
(4.10)
Diese Gleichung lässt sich nach xc auflösen
xc =
k
∆Θ
− ∆xc
− ∆xc
∆k · leff
∆k
(4.11)
Unbekannt sind hier die Größen ∆Θ und ∆xc . Um diese zu ermitteln wird das OptikModell benötigt. Dazu wird die Strahlposition ~x = (xBPM1 , . . . ,xBPM54 )T im Speicherring
vor und nach der ∆k-Variation aufgezeichnet, wobei die 54 Elemente von ~x die Strahlablage in allen 54 Strahllagemonitoren beschreiben. Die Differenz
∆~xgem. = ~xk+∆k − ~xk
(4.12)
43
Kapitel 4. Strahlbasierte Messmethoden
beschreibt die Antwort des Strahls auf die ∆k-Variation. Im Optik-Modell wurden mittig
in den Quadrupolen virtuelle Dipolkorrektoren als dünne Elemente eingefügt. Der virtuelle Dipolkorrektor, der im Modell dem Quadrupol zugeordnet ist, dessen k-Wert variiert
wurde, wird jetzt dazu verwendet die gemessene Orbitantwort auf die ∆k-Variation zu
simulieren. Ein in MATLAB geschriebener Algorithmus vergleicht die gemessene Orbitantwort ∆~xgem mit der simulierten ∆~xsim . Ein quadratischer Minimierungs-Algorithmus
minimiert dazu die Differenz
∆~x = ∆~xsim − ∆~xgem
(4.13)
durch Variation des Ablenkwinkels ∆Θsim. des virtuellen Dipolkorrektors. Aus dem Winkel Ablenkwinkels ∆Θsim. , bei dem die Differenz minimal ist, erhält man die Änderung
des Ablenkwinkel ∆Θ und der Ablage ∆xc . Mit (4.8), (4.11) und den bekannten Größen
α
β
θ
xg
β
α
s12
s23
Abbildung 4.3.: Skizze zur geometrischen Berechnung der Höhe des Dreiecks, das aus
der Triplettachse und dem Orbit ohne ∆k aufgespannt wird
∆k, k und leff lässt sich der Gesamtablenkwinkel Θ im mittleren Quadrupol berechnen.
Mit Kenntnis dieses Winkels Θ und der Abstände s12 und s23 der Quadrupole voneinander lässt sich die Höhe xg des Dreiecks, das aus der Triplettachse und dem Orbit ohne
∆k (vgl. Abb. 4.2) aufgespannt wird, berechnen. Diese lässt sich durch geometrische
Betrachtungen, vgl. Abb. 4.3, zu
r
s12 + s23
(s12 + s23 )2
xg =
− sgnΘ
+ s12 · s23
2 tan Θ
2 tan2 Θ
(4.14)
berechnen. Die ausführliche Rechnung ist in [12] dargestellt. Setzt man (4.11) und (4.14)
in (4.7) ein, so erhält man die gesuchte Quadrupolfehlaufstellung bezüglich der TriplettAchse
xoff = xg − xc
44
(4.15)
4.2. Bestimmung von Quadrupolfehlaufstellungen
4.2.2. Korrektorbasierte Methode
Eine alternative Methode wurde im Rahmen dieser Arbeit bei DELTA neu eingeführt
und untersucht. Die Methode basiert ebenfalls auf der Variation der Quadrupolstärke ∆k
des mittleren fokussierenden Quadrupols. Die dadurch entstehende Orbitänderung wird
mit dem auf dem mittleren Quadrupol montierten Korrektor kompensiert. Es wird dabei
ausgenutzt, dass sich auf den mittleren Triplettquadrupolen horizontale Dipolkorrektorspulen befinden, die den Strahl in der Ebene ablenken, in der der Quadrupol fokussierend
wirkt. Ist die ∆k-Orbitänderung kompensiert, lässt sich aus der Korrektor- und Quadrupolstärke die Fehlaufstellung des mittleren Quadrupols bezüglich der Triplettachse
bestimmen.
Messprinzip
Ein fehlaufgestellter Quadrupol erzeugt ein Dipolfeld in Bezug auf den Sollorbit, das den
Strahl nach (2.23) um den Winkel
ΘQuad = k · xoff · leff
ablenkt. Dies verändert den Closed-Orbit nach (2.27) gemäß
p
p
β(s)
ΘQuad βj cos(νϕ(s) − νϕj + νπ)
uco,Quad (s) =
2 sin πν
(4.16)
(4.17)
Das Dipolfeld, das durch die auf dem Quadrupol montierten Korrektorspulen erzeugt
wird, lenkt den Strahl nach (2.22) gemäß
ΘK =
1
· leff
R
ab. Dies ändert den Closed Orbit ebenfalls gemäß (2.27) um
p
p
β(s)
uco,K (s) =
ΘK βj cos(νϕ(s) − νϕj + νπ)
2 sin πν
(4.18)
(4.19)
Wählt man nun ΘK so, dass ΘQuad grade kompensiert wird gilt
uco,Quad (s) + uco,K (s) = 0
(4.20)
Da sich bei DELTA die horizontalen Korrektoren auf den horizontal fokussierenden Quadrupolen am gleichen Ort auf dem gleichen Magneteisen befinden, sind in (4.17) und
(4.19) Betafunktion βj und Phasenvorschub ϕj am Ort von Quadrupol und Korrektor
identisch, auch die effektive Länge leff beider Magneten ist die gleiche. Es folgt dann aus
(4.20) mit (4.17) und (4.19)
ΘQuad = −ΘK
(4.21)
45
Kapitel 4. Strahlbasierte Messmethoden
und mit (4.16) und (4.18)
k · xoff = −
1
R
(4.22)
Es wird allerdings nicht der Gesamtablenkwinkel durch die Quadrupolfehlaufstellung betrachtet, sondern nur die Veränderung des Closed-Orbits bei einer zusätzlichen Bestromung des Quadrupol. Dazu wird der Strahl durch die magnetischen Zentren der äußeren
Quadrupole des zu vermessenden Tripletts geführt. Der daraus resultierende Strahlverlauf
im Triplett ist in Abb. 4.4 skizziert. Ändert man die Stärke k des mittleren Quadrupols
xc
xg
xoff
BPM
BPM
θ
s12
SollOrbit
QD
ΔθCorr
ΔθQuad
s23
QF
QD
Abbildung 4.4.: Schematische Darstellung des Verlaufs des Elektronenstrahls in einem
Quadrupoltriplett, bestehend aus zwei defokussierenden Quadrupolen und einem fokussierenden Quadrupol, bei einer Fehlaufstellung xoff des mittleren, fokussierenden Quadrupols. Die gestrichelten Linien skizzieren die Strahlablenkung durch die ∆k-Variation bzw.
durch den Korrektor. Insgesamt kompensieren sich beide so, dass der Orbit unverändert
bleibt.
um einen gewissen Wert ∆k, so wird der Strahl von diesem, je nach Vorzeichen des ∆k,
stärker oder schwächer abgelenkt. Dies führt zu einem neuen Closed-Orbit. Benutzt man
den auf dem Quadrupol montierten Dipolkorrektor um diese Closed-Orbit-Änderung zu
kompensieren, bleibt der Orbit insgesamt unverändert. Durch die Änderung der Fokussierung ändert sich der Arbeitspunkt („tune“), daher sollte ∆k k sein. In Abb. 4.4 ist dies
für eine zusätzliche Bestromung des fokussierenden Quadrupols in der Mitte des Tripletts
skizziert. Der Strahl hat im mittleren Quadrupol die Ablage xc von der magnetischen
Mitte. Die Winkeländerung durch das ∆k lässt sich durch
Θ∆k = ∆k · xc · leff
46
(4.23)
4.2. Bestimmung von Quadrupolfehlaufstellungen
ausdrücken. Der Korrektor wird nur dazu genutzt die Closed-Orbit-Änderung durch das
∆k zu kompensieren, daher wird hier aus (4.22)
∆k · xc = −
1
R
(4.24)
Durch eine Messung der Änderung der Quadrupolstärke ∆k und des Krümmungsradius
des Korrektors erhält man im Gleichgewichtsfall (Closed-Orbit-Störungen durch ∆k und
Dipolkorrektor kompensieren sich gerade) die Strahlposition xc im mittleren Quadrupol
xc = −
1
R · ∆k
(4.25)
Damit lässt sich dann der Gesamtkickwinkel Θ über
Θ = xc · k · leff
(4.26)
des Quadrupols berechnen. Über die geometrischen Betrachtungen des Strahlverlaufs im
Triplett aus Kap. 4.2.1 und Abb. 4.3 erhält man mit (4.14)
r
(s12 + s23 )2
s12 + s23
− sgnΘ
+ s12 · s23
xg =
2 tan Θ
2 tan2 Θ
(4.27)
und (4.15) die Quadrupolfehlaufstellung
xoff = xg − xc
(4.28)
Dabei sind s12 und s23 die Abstände zwischen den Quadrupolen, wie in Abb. 4.4 dar-
2
quad. Orbitabw. [mm ]
0.12
-2
∆ k = -0.035 m
0.1
0.08
0.06
0.04
0.02
0
-3
-2
-1
K orrektor R -1 [m-1 ]
Abbildung
4.5.:
0
1
x 10
-5
Quadratische Orbitabweichung in Abhängigkeit von R−1 bei
gegebenem ∆k.
gestellt. Nachdem der in Abb. 4.4 skizzierte Strahlverlauf eingestellt wurde, wird der
Orbit referenziert. Dann die Fokussierstärke des mittleren Quadrupols um ∆k verändert.
47
Kapitel 4. Strahlbasierte Messmethoden
Der resultierenden Closed-Orbit-Änderung wird der Korrektor schrittweise entgegen gefahren. Dabei wird nach jedem Schritt die Strahlposition in den Strahllagemonitoren
gemessen und die quadratische Abweichung des Orbits von der Orbitreferenz ermittelt.
Dies geschieht solange, bis die quadratische Orbitabweichung ein Minimum durchlaufen
hat (vgl. Abb. 4.5).
−1
Die Korrektorstärke Rmin
, bei der diese minimal wird, ergibt mit dem ∆k nach (4.25)
einen Wert für xc . Die Messung wird für schrittweise anwachsende ∆k wiederholt. Aus
−1
den Wertepaaren (∆k,Rmin
), bei denen die quadratische Orbitabweichung zur Referenz
minimal wird, erhält man durch lineare Regression gemäß
−1
Rmin
= xc · ∆k + const.
(4.29)
die Strahlposition in Bezug auf die magnetische Mitte des Quadrupols als Steigung
xc =
−1
d(Rmin
)
d(∆k)
(4.30)
der Regressionsgeraden. Mit (4.26)-(4.28) lässt sich dann die Fehlaufstellung des mittleren
Quadrupols in Bezug auf die Triplett-Achse bestimmen.
48
5. Diskussion und Analyse der
verwendeten Messmethoden
In diesem Kapitel werden die vorgestellten strahlbasierten Messmethoden auf störende Einflüsse hin untersucht. Entsprechend der Reihenfolge im vorangegangenen Kapitel
wird mit der Analyse der strahlbasierten Messmethode zur Bestimmung der Offsets der
Strahllagemonitore begonnen. Dabei wird der Einfluss der Dipolkorrektoren auf die Messmethode untersucht. Anschließend werden die beiden strahlbasierten Messmethoden zur
Bestimmung von Aufstellungsfehlern der Quadrupole gegenübergestellt. Im Fall der neu
eingeführten korrektorbasierten Messmethode wird dabei auch auf die Genauigkeit der
Methode eingegangen.
5.1. Strahlbasierte Methode zur Bestimmung von Offsets
der Strahllagemonitore
Zunächst soll die bei DELTA verwendete strahlbasierte Messmethode zur Bestimmung
der Offsets der Strahllagemonitore [8, 9] auf den Störeinfluss der Dipolkorrektoren hin
untersucht werden.
Anwendung an DELTA
Bei DELTA erfolgt die ∆k-Änderung der Fokussierstärke eines einzelnen Quadrupols,
die für die Messmethode nötig ist, mit Hilfe der Relaiskaskade (vgl. Kap. 3.2.3). Alle
verwendeten Komponenten des Speicherrings (Strahllagemonitore, Relaiskaskade, Quadrupole) können in normalem Betriebszustand verwendet und aus dem Kontrollraum
gesteuert werden. Ein Umbau ist somit nicht erforderlich. Im Kontrollsystem steht ein
Software-Werkzeug zur Verfügung, das eine automatische Vermessung der Strahllagemonitore ermöglicht [7].
Auf den meisten DELTA-Quadrupolen, die mit einem Strahllagemonitor ausgestattet
sind, zusätzliche Dipolkorrektorspulen montiert, die zur Erzeugung ihres Dipolfeldes das
Quadrupoljoch nutzen. Den Quadrupolfeldern sind somit Dipolfelder überlagert, die zur
Orbitkorrektur oder zur Erzeugung von Orbitbeulen genutzt werden. Für das Aufspannen
49
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
Orbitbeulen verschiedener Ablage, die nach außen hin abgeschlossen sind, müssen die
Dipolkorrektoren für jede Ablage in ihrer Stärke relativ zueinander verändert werden.
Die zur Vermessung der Offsets der Strahllagemonitore nötigen Orbitbeulen können
zunächst durch alle zur Verfügung stehenden Dipolkorrektoren erzeugt werden. Dabei
kann auch der Dipolkorrektor verwendet werden, der auf dem Quadrupol selbst montiert
ist, dessen Achse den Bezugspunkt bei der Vermessung des Offsets des Strahllagemonitors
bildet. Für jeden neuen Messpunkt wird somit die Stärke dieses Dipolkorrektors verändert. Der Einfluss eines Dipolkorrektors auf die Messmethode bei variabler Bestromung
soll in Kap. 5.1.2 untersucht werden.
Es besteht des Weiteren die Möglichkeit die Bestromung einzelner Dipolkorrektoren
konstant zu halten. Das bedeutet, dass der Dipolkorrektor gegebenenfalls eingeschaltet
bleibt, aber während der Messung nicht in seiner Stärke verändert wird. In diesem Fall
muss zur Erzeugung der Orbitbeule eine andere Linearkombination aus drei oder mehr
der zur Verfügung stehenden Dipolkorrektoren verwendet werden. Da bei DELTA insgesamt 30 horizontale und 26 vertikale Dipolkorrektoren zur Verfügung stehen, können auch
bei einer Fixierung des Dipolkorrektors Beulen mit variable Ablage x in dem betreffenden Strahllagemonitor erzeugt werden. Der Einfluss eines Dipolkorrektors mit konstanter
Bestromung auf die Messmethode soll im Folgenden untersucht werden.
5.1.1. Einfluss eines zeitlich konstanten Dipolkorrektorfeldes
Zunächst soll der Fall untersucht werden, bei dem der Strom des Dipolkorrektors konstant gehalten wird und somit nur statisch an der Bildung der Orbitbeule teilnimmt. In
erster Ordnung erzeugt der Dipolkorrektor ein Dipolfeld, das sich dem Quadrupolfeld
überlagert. Ein Dipolfeld ist nach Definition zwischen den Polschuhen ortsunabhängig
und führt zu einer Verschiebung des Zentrums des Quadrupolfeldes.
Wird die Fokussierstärke k des Quadrupols um ∆k verändert, so verändert sich nur
der Gradient des Quadrupolfeldes, nicht aber der konstante Offset durch das Dipolfeld
des Korrektors.
An einer beliebigen horizontalen Position x hat das reine Quadrupolfeld ohne Dipoloffset und zusätzlichem ∆k nach (2.9) die Stärke
e
By (x) = k · x
p
(5.1)
Mit dem zusätzlichen ∆k erhöht sich die Feldstärke um ∆B(x)
e
(By (x) + ∆By (x)) = (k + ∆k) · x
p
(5.2)
Den Feldstärkeunterschied ∆By (x) erhält man, indem man (5.1) von (5.2) subtrahiert
e
∆By (x) = ∆k · x
p
50
(5.3)
5.1. Strahlbasierte Methode zur Bestimmung von Offsets der Strahllagemonitore
Betrachtet man nun an der gleichen horizontalen Position x das Quadrupolfeld mit Dipoloffset einmal ohne und einmal mit ∆k so erhält man
e
1
By (x) = + k · x
(5.4)
p
R
e
1
(By (x) + ∆By (x)) = + (k + ∆k) · x
(5.5)
p
R
Subtrahiert man (5.4) von (5.5), so ergibt sich für den Feldstärkeunterschied ∆By (x)
ebenfalls
e
∆By (x) = ∆k · x
p
(5.6)
Die durch die ∆k-Variation hervorgerufene Änderung des Ablenkwinkels ∆Θ = leff ·∆k ·x
wird durch ein Dipolfeld, das während der gesamten Messung konstant bleibt, nicht
beeinflusst. Somit gilt für die quadratische Ablage bei einem konstantem Dipolfeld, dass
diese nach (4.5)
∆x2 ∝ x2
(5.7)
nur von der eingestellten Orbitablage x im betreffenden Strahllagemonitor abhängig ist.
Das zeitlich konstante Feld eines Dipolkorrektors hat somit in erster Ordnung keinen
Einfluss auf die strahlbasierte Offset-Bestimmung des Strahllagemonitors.
Messergebnisse
Um die theoretischen Ergebnisse des vorangegangenen Abschnitts experimentell zu bestätigen wurde eine Messreihe durchgeführt, in der der Dipolkorrektorstrom zwar konstant
war, aber für die einzelnen Offsetmessungen auf verschiedene Stärken eingestellt wurde.
In Abbildung 5.1 sind die ermittelten Monitor-Offsets gegen die Bestromung des Dipolkorrektors aufgetragen. Es ist zu beobachten, dass auch für gleiche Dipolkorrektorstärken
die gemessenen Offsets des Strahllagemonitors im Bereich 30 µm bis 50 µm streuen. Die
gemessenen Offsets streuen um ∼ 140 µm. Dies liegt im Bereich der Messgenauigkeit
von ±(20 bis 100) µm des Verfahrens bei DELTA [9]. Insgesamt konnte keine Aussage zu
einer Systematik gemacht werden.
Der Dipolkorrektor sollte also bei der Anwendung dieser Messmethode, sofern dies
möglich ist, nicht bestromt werden. Bei einigen Strahllagemonitoren führt dies allerdings
zu einem Strahlverlust. In diesem Fall sollte der Dipolkorrektor während der Messung in
seiner Bestromung konstant gehalten werden, um den Einfluss auf die Messung gering zu
halten.
5.1.2. Einfluss eines zeitlich veränderlichen Dipolkorrektorfeldes
Wird der Dipolkorrektor dazu verwendet die Orbitbeule mit Ablage x im Strahllagemonitor zu erzeugen, so verändert sich seine Stärke bei jedem neuen Messpunkt für den
51
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
0.12
0.1
B P M-Offs et x off [mm]
0.08
0.06
0.04
0.02
0
-0.02
-0.04
-0.06
-1
0
1
2
3
4
5
K orrektors trom I [A]
6
7
8
9
∆K
Abbildung 5.1.: Strahlbasiert bestimmte Offsets des Strahllagemonitors „bpm36“ in Abhängigkeit von der Bestromung des Dipolkorrektors „vk18“. Jeder Punkt ist das Ergebnis
einer eigenständigen Messung des Offsets des Strahllagemonitors.
eine neue Ablage x benötigt wird. Die dazu nötigen Korrektorströme variieren im Bereich einiger Ampere. Während der ∆k-Variation ist das Dipolfeld jeweils konstant, so
dass für die einzelnen Messpunkte die Ergebnisse aus Kap. 5.1.1 gelten. Zwischen den
Messpunkten ändert sich jedoch die Stärke des Dipolfeldes. Die Änderung der Magnetfeldstärke im Quadrupol kann nicht als klein angenommen werden. Somit kann auch die
Änderung der Magnetisierung des Quadrupoljoches nicht als klein angenommen werden.
Durch diese ist der k-Wert und der ∆k-Wert der einzelnen Messpunkte nicht konstant.
Dies führt dazu, dass die einzelnen Messwerte nicht miteinander vergleichbar sind und
sehr stark um die Parabelform streuen.
Messergebnisse
Hierzu wurde eine Vergleichsmessung durchgeführt, bei der der vertikale Offset des Strahllagemonitors „bpm36“ bestimmt wurde. Die Messung wurde dabei einmal mit konstanter
Bestromung des Dipolkorrektors „vk18“, welcher auf dem betreffenden Quadrupol montiert ist, durchgeführt und einmal mit variabler Bestromung. Die beiden Messungen sind
in Abb. 5.2 dargestellt. Die Messung mit konstanter Dipolfeldstärke liefert sehr gute
Messergebnisse, die nur wenig um die erwarteten Parabelform streuen. In diesem Fall
ist eine Bestimmung des Offsets des Strahllagemonitors möglich und wird nur durch die
52
5.1. Strahlbasierte Methode zur Bestimmung von Offsets der Strahllagemonitore
Abbildung 5.2.: Quadratische Orbitabweichung bei einer ∆k-Variation der Quadrupolstärke in Abhängigkeit von der Strahlposition im Strahllagemonitor „bpm36“. links:
Dipolfeldstärke von „vk18“ variabel. rechts: Dipolfeldstärke von „vk18“ konstant.
relative Genauigkeit der Strahllagemonitore limitiert. Die Messergebnisse bei variabler
Dipolfeldstärke streuen extrem stark, so dass das Anpassen einer Parabel nicht möglich ist. Eine Bestimmung des Offsets ist bei einer zeitlich veränderlichen Dipolfeldstärke
nicht möglich.
Der Dipolkorrektor, der auf dem Quadrupol montiert ist, dessen Achse den Bezugspunkt für die Kalibration des Strahllagemonitors darstellt, muss daher in seiner Feldstärke konstant gehalten werden, um eine strahlbasierte Bestimmung seines Offsets zu
ermöglichen.
53
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
5.2. Modellbasierte Methode zur Bestimmung von
Quadrupolfehlaufstellungen
In diesem Kapitel soll die modellbasierte Messmethode zur Bestimmung von Aufstellungsfehlern der Triplettquadrupole auf Störeinflüsse hin untersucht werden.
5.2.1. Einfluss von Magnetfeldern unterschiedlicher Ordnung
Die Messmethode geht von der vereinfachten Annahme aus, dass die Quadrupoltripletts
ausschließlich aus drei Quadrupolen bestehen, vgl. Abb. 4.2. Da für die Methode vorausgesetzt wird, dass der Strahl in den äußeren Triplettquadrupolen keine Ablage besitzt,
kann der Strahl somit nur vom mittleren Triplettquadrupol abgelenkt werden. Daher werden alle Strahlablenkungen, die innerhalb des Tripletts auf den Strahl wirken, vollständig
dem mittleren Quadrupol zugeordnet. Sind innerhalb des zu vermessenden Tripletts zusätzlich zum Feld des mittleren Quadrupols weitere Magnetfelder vorhanden, so wird
deren Wirkung auf den Strahl ebenfalls dem mittleren Quadrupol zugeordnet. Aus diesem Grund werden im Folgenden die bei DELTA möglichen Störfelder und ihr Einfluss
auf die Messmethode diskutiert.
Dipol-Felder
Zur Orbitkorrektur wurden in DELTA insgesamt 56 (30 horizontale und 26 vertikale)
Dipol-Korrektoren eingebaut. Diese wurden durch zusätzliche Spulenwindungen auf den
Quadrupolen realisiert. In der bei DELTA verwendeten Triplett-Struktur befindet sich
auf dem mittleren horizontal fokussierenden Quadrupol immer ein horizontal ablenkender
Dipolkorrektor. Ist dieser bestromt, so erzeugt er ein zusätzliches Dipolfeld, das den Strahl
zusätzlich zum Quadrupolfeld um den Winkel ΘK ablenkt
Θges = ΘQ + ΘK
(5.8)
Dabei beschreibt der Winkel ΘQ die Ablenkung des Strahls durch den Quadrupol. Damit der Algorithmus das richtige Ergebnis liefert, muss gemäß (5.8) ΘK aus ΘQ heraus
gerechnet werden, sollte ΘK von Null verschieden sein.
Um diese Korrektur zu vermeiden, sollte der Dipolkorrektor daher ausgeschaltet werden.
Sextupol-Felder
Neben vielen Quadrupolen befinden sich Sextupolmagnete, welche ein nichtlineares Magnetfeld erzeugen. Diese Sextupolmagnete sind bei DELTA in Strahlrichtung entweder
54
5.2. Modellbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
direkt hinter den Quadrupolen, oder durch interne Zusatzspulen in den Quadrupolen realisiert (vgl. Kap. 3.1.2). Durch nichtlineare Sextupolfelder innerhalb des zu vermessenden
simulierter
Strahlverlauf
BPM
SollOrbit
realer
Strahlverlauf
QD
BPM
ZusatzKick
QF
S
QD
Abbildung 5.3.: Schematische Darstellung des Verlaufs des Elektronenstrahls in einem
Quadrupol-Triplett, bestehend aus 2 defokussierenden Quadrupolen „QD“, einem fokussierenden Quadrupole „QF“ und einem Sextupolmagneten „S“ der direkt hinter dem „QF“
montiert ist, bei einer gemeinsamen Fehlaufstellung xoff des mittleren, fokussierenden
Quadrupols und des Sextupols.
Triplett verliert die lineare Näherung bei der Simulation der Orbitantwort auf die ∆kVariation ihre Gültigkeit, da die Orbitantwort durch Bilden des Differenzorbits ermittelt
wird. Bei der Differenzbildung geht gerade die Information der absoluten Strahlposition
im Sextupol verloren. Die gemessene Orbitantwort in nichtlinearen Feldern hängt somit
von der absoluten Strahllage in diesen ab. Hat der Strahl im realen Sextupol die Ablage
xSext. , so wird er von diesem um
ΘSext. = m · x2Sext. · leff
(5.9)
abgelenkt. Ändert sich in Folge der ∆k-Störung des Closed-Orbits die Ablage im Sextupol
um ∆xSext. , so wird der Strahl von diesem nun um
ΘSext. + ∆ΘSext. = m · (xSext. + ∆xSext. )2 · leff
(5.10)
abgelenkt. Somit folgt für die Änderung der Strahlablenkung ∆ΘSext. durch den Sextupol
∆ΘSext.,real = m · (xSext. ∆xSext. + ∆x2Sext. ) · leff
(5.11)
In der Simulation wird die Orbitantwort in Bezug auf den Sollorbit betrachtet, d.h.
xSext. = 0, der Sextupol lenkt den Strahl in der Simulation somit nur um
∆ΘSext.,sim = m · ∆x2Sext. · leff
(5.12)
55
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
ab. Der Beitrag der Sextupole zum Closed-Orbit ist in der Simulation also viel kleiner
als in der Realität, da ∆xSext. xSext. Der Algorithmus des Verfahrens muss dann den
virtuellen Dipolkorrektor zusätzlich verstärken um die zusätzliche Strahlablenkung durch
den Sextupol bei der Simulation der Orbitantwort zu berücksichtigen. Der stärkere Dipolbeitrag wird dann der Quadrupolfehlaufstellung zugeordnet. Das Verfahren ermittelt
also eine um den Sextupolbeitrag falsche Fehlaufstellung. Um diesen Fehler zu vermeiden
müssen die Sextupole vor der Messung ausgeschaltet werden.
5.2.2. Untersuchung der Größenordnung des Einflusses der
Sextupolmagnete
Zur Untersuchung der Größenordnung des Einflusses der Sextupolmagnete auf die Bestimmung der Fehlaufstellung wurde am Triplett um den Quadrupol „qf03+06“ Messreihen mit und ohne eingeschaltete Sextupolmagnete aufgenommen. Die Messungen wur0.65
interne/externe S extupole aus
interne/externe S extupole ein
0.6
F ehlaufs tellung xoff [mm]
0.55
0.5
0.45
0.4
0.35
0.3
0.25
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
K as kadens trom I ∆K [A]
-0.1
0
Abbildung 5.4.: Strahlbasiert bestimmte Fehlaufstellung des Quadrupols „qf03+06“
in Abhängigkeit von dem verwendeten ∆k-Strom, bei ein- und ausgeschalteten internen/externen Sextupolen.
den jeweils für verschiedene Zusatzmagnetströme bzw. ∆k-Werte durchgeführt. Für die
Auswertung der Orbitantwort wurden im DELTA-Modell [12] ebenfalls die Sextupole
deaktiviert. Die Ergebnisse in Abhängigkeit vom Kaskadenstrom I∆k sind in Abb. 5.4
dargestellt. Die Anwesenheit der Sextupolfelder führte in diesem Fall zu einem Offset der
56
5.2. Modellbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
gemessenen Fehlaufstellung von etwa 160 µm. Es lassen sich allerdings nicht alle Sextupolfelder in DELTA ausschalten, da die Dipolkorrektoren starke Sextupolfelder erzeugen
und diese aufgrund der Fehlaufstellungen der Quadrupole nicht ausgeschaltet werden können. Da die Sextupolkomponenten der Dipolkorrektoren in der gleichen Größenordnung
liegen, wie die der internen Sextupolmagnete, ist zu erwarten, dass diese die Messung in
ähnlicher Stärke beeinflussen wie die externen/interen Sextupole.
5.2.3. ∆k-Abhängigkeit der bestimmten Fehlaufstellung
In Abb. 5.4 ist neben dem Offset, der durch zusätzliche Strahlablenkung des Sextupolfeldes innerhalb des Tripletts verursacht wird, eine Abhängigkeit der gemessenen Fehlaufstellung von dem angelegten Zusatzstrom I bzw. ∆k-Wert zu erkennen. Dieser Effekt ist
sowohl bei der Messung mit eingeschalteten internen/externen Sextupole zu erkennen,
als auch bei der Messung bei der diese ausgeschaltet sind.
Die durch die ∆k-Störung verursachte Orbitänderung wächst nach (4.3) in der linearen Strahloptik linear mit ∆k. Betrachtet man die gemessene Orbitantwort auf die ∆kStörung, siehe Abb. 5.5, so zeigt sich allerdings ein nichtlineares Verhalten. Dieses nicht0.2
interne/externe S extupole aus
interne/externe S extupole ein
0.18
mittlere Orbitaenderung [mm]
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
K as kadens trom I ∆K [A]
-0.1
0
Abbildung 5.5.: Mittlere absolute Orbitänderung als Funktion der ∆k Zusatzströmen
für die Messreihe mit ein- und ausgeschalteten internen/externen Sextupolen.
lineare Verhalten zeigt sich sowohl bei der Messung mit eingeschalteten internen/exteren
57
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
Sextupolen, als auch bei der mit ausgeschalteten Sextupolen. An beide Messreihen wird
ein Polynom 2. Grades
y(x) = a2 · x2 + a1 · x + a0
(5.13)
angepasst, die Ergebnisse sind in Tab. 5.1 aufgeführt. Es zeigt sich, dass der Koeffizient
interne/externe
interne/externe
Sext. aus [mm]
Sext. ein [mm]
a0
0,057
0,012
a1
0,121
0,148
a2
0,099
0,247
Koeffizient
Tabelle 5.1.: Koeffizienten des angepassten Polynoms 2. Grades an die in Abb. 5.5
dargestellten Messreihen.
des linearen Terms a1 für beide Messreihen etwa gleich groß ist. Er gibt das lineare Verhalten der ∆k-Störung wieder. Der Koeffizient des quadratischen Terms a2 ist bei der
Messreihe mit eingeschalteten Sextupolen deutlich größer, als bei der mit ausgeschalteten.
Durch die lineare Orbitänderung durch das ∆k durchläuft der Strahl die nichtlinearen
Felder der Sextupole und Korrektormagnete mit anderer Ablage und erzeugt dadurch
weitere Orbitstörungen, die quadratisch mit ∆k wachsen. Da bei ausgeschalteten internen/externen Sextupolen die Anzahl der nichtlinearen Felder im Speicherring stark
reduziert ist, sinkt auch die Anzahl der nichtlinearen Orbitstörungen und damit auch
der Koeffizient a2 . Die Stärke der nichtlinearen Orbitstörungen wächst mit ∆k und wird
durch das Modell nicht korrekt simuliert. Der Algorithmus ordnet auch diese zusätzliche Orbitstörung dem mittleren Quadrupol des Tripletts zu und liefert so eine zu große
Fehlaufstellung, die mit ∆k anwächst.
5.2.4. Genauigkeit und Iterative Anwendung der modellbasierten
Messmethode an DELTA
Durch Vergleich der gemessenen ∆k-Orbit-Änderung mit der simulierten Orbit-Änderung
lässt sich mit dieser Methode Richtung und Wert der Quadrupolfehlaufstellung bezüglich
der Triplettachse bestimmen. Da das Optik-Modell aufgrund der störenden Sextupolfelder der Sextupolmagnete, wie auch der Dipolkorrektoren, nur innerhalb gewisser Grenzen
in der Lage ist den Strahlverlauf in der realen Maschine wiederzugeben, führt dies dazu, dass zwar die Richtung der Fehlaufstellung korrekt ermittelt wird, der Betrag aber
häufig zu groß ist [12]. Das Verfahren wird daher iterativ, durch abwechselndes Messen
und Korrigieren der Quadrupolposition um einen Teil der gemessenen Fehlaufstellung,
angewendet.
58
5.3. Korrektorbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
5.3. Korrektorbasierte Methode zur Bestimmung von
Quadrupolfehlaufstellungen
Im Rahmen dieser Arbeit wurde die korrektorbasierte Messmethode entwickelt und in
Form eines MATLAB-Programms1 in das Kontrollsystem von DELTA implementiert.
Nach der Auswahl der Messparameter3 übernimmt das Programm die Steuerung der
Abbildung 5.6.: Graphische Nutzeroberfläche des Messprogramm.
Magnetströme und die Auswertung des Orbits automatisch. Aus den Nutzereingaben
bildet das Programm äquidistante ∆k-Zusatzströme, die nacheinander angefahren werden. Vor dem Setzen von Magnetströmen wird der Orbit referenziert und gespeichert. Alle
Orbitabweichungen werden immer in Bezug auf diese Referenz ermittelt. Zur Messung eines Orbits werden die EPICS-Records der Strahllagemonitore mehrfach im 0,1 s-Abstand
abgefragt und über die erhaltenen Werte gemittelt um Rauschen zu minimieren. Ist ein
∆k-Wert gesetzt, setzt das Programm schrittweise den entsprechenden Korrektorstrom.
Nach jedem Schritt wird der Orbit gemessen und die quadratische Orbitabweichung zur
Orbitreferenz berechnet. Der erhaltene Wert wird zusammen mit dem gesetzten Korrektorstrom gespeichert und graphisch im Nutzerinterface dargestellt. Bei jedem Schritt
1
MATLAB greift über die API2 -Erweiterung labca auf EPICS-Records schreibend und lesend zu und
kann diese auch verändern.
API (engl.): Application Programming Interface
3
Die Variablen bei der Messung sind Kaskadenstrom I∆k und der Korrektorstrom IKorrektor , sowie die
2
Anzahl der Messpunkte
59
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
wird die quadratische Orbitabweichung, bei richtiger Wahl des Vorzeichens des Korrektorstroms, kleiner. Das Programm erhöht den Korrektorstrom schrittweise bis die Orbitabweichung ein Minimum durchlaufen hat (vgl. Abb. 5.7). Der Korrektorstrom des Minimums wird zusammen mit dem gesetzten ∆k-Zusatzstrom mit dem Programm i2k [7] in
die Multipolstärken k und R−1 umgerechnet und gespeichert. Dann wird der Korrektorstrom wieder auf Null gesetzt und die Messreihe mit dem nächsthöheren ∆k-Zusatzstrom
−1
wiederholt. Die Wertepaare (∆k,Rmin
) werden ebenfalls graphisch in der Nutzeroberflä-
che des Messprogramms dargestellt. Sind drei oder mehr Wertepaare ermittelt worden,
wird eine Regressionsgerade an sie angepasst. Aus den Fitparametern wird dann gemäß
dem vorangegangenen Kapitel die Fehlaufstellung des mittleren Quadrupols im Triplett
ermittelt. Wahlweise können alle aufgenommenen Orbit- und Magnetstromdaten gespeichert werden um eine nachträgliche erneute Auswertung zu ermöglichen.
5.3.1. Einfluss von Magnetfeldern unterschiedlicher Ordnung
Die korrektorbasierte Methode zur Messung von Quadrupolfehlaufstellungen basiert, wie
die modellbasierte Methode, auf den geometrischen Betrachtungen aus Abb. 4.3. Das
bedeutet, dass auch bei dieser Methode alle Strahlablenkungen, die zwischen den beiden
äußeren Quadrupolen auf den Strahl wirken, einzig dem mittleren Quadrupol des Triplett
zugeordnet werden. Alle zusätzlichen Strahlablenkungen, die nicht von den Quadrupolen
stammen, beeinflussen somit das Ergebnis der Bestimmung der Fehlaufstellung.
Dipolfelder
Ist der Dipolkorrektor auf dem mittleren Quadrupol vor Beginn der Messung nicht ausgeschaltet worden, so lenkt er den Strahl zusätzlich um den Winkel ΘKorrektor ab. Dies
verändert dann auch die Form der Dreiecksgeometrie (Abb. 4.3). Auch bei dieser Methode
würde dann dem mittleren Quadrupol ein zu großer Ablenkwinkel zugeordnet werden. Da
die Bestromung des Korrektors bekannt ist, kann der Gesamtablenkwinkel der Triplettmitte um den Beitrag des Korrektors korrigiert werden. Das Dipolfeld des Korrektors, der
sich auf einem langen Quadrupoljoch befindet, ist bei bekannter Bestromung aber nur
auf besser als 6% genau. Dadurch ergibt sich ein zusätzlicher Fehler bei der Bestimmung
der Fehlaufstellung. Da dies ein vermeidbarer Fehler ist, wird der Korrektor vor Beginn
der Messung immer ausgeschaltet und nur zum Ausgleich der ∆k-Störung verwendet.
Sextupolfelder
Anders als bei der modellbasierten Methode wird hier kein Differenzorbit betrachtet. Der
Einfluss der Sextupolfelder des Speicherrings bleibt also während der gesamten Messung
60
5.3. Korrektorbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
konstant, da der Orbit konstant bleibt. Auf Grund der geometrischen Betrachtungen
des Strahlverlaufs innerhalb des Tripletts muss aber der Einfluss aller Sextupole innerhalb des zu vermessenden Tripletts betrachtet werden. Da aber die Strahlposition in
den Triplettsextupolen unbekannt ist, ist auch deren Beitrag zur Strahlablenkung der
Triplettmitte unbekannt und lässt sich somit nicht korrigieren. Daher wird die Fehlaufstellung, abhängig von der Strahlablage in den Triplettsextupolen, falsch bestimmt. Die
Triplettsextupole müssen also ausgeschaltet werden um diesen systematischen Fehler zu
vermeiden.
5.3.2. Bestimmung der zur ∆k-Kompensation nötigen Korrektorstärke
Eine mit der korrektorbasierten Methode durchgeführte Messreihe am Quadrupoltriplett
um „qf03+02“ ist in Abb. 5.7 exemplarisch dargestellt. Es ist deutlich zu erkennen, dass
die Messwerte den erwarteten parabelförmigen Verlauf zeigen.
−1
über einen Fit 2. Ordnung
Bestimmung der Korrektorstärke Rmin
−1
Die Bestimmung des Wertes von Rmin
ist durch Anpassen eines Polynoms 2. Ordnung
y(x) = ax2 + bx + c
(5.14)
an die Wertepaare (R−1 ,quad. Orbitabweichung) möglich. Dies ist in Abb. 5.7 exempla−1
risch dargestellt. Die Werte für Rmin
ergeben sich dabei als Minimum von (5.14)
−1
Rmin
=−
b
2a
(5.15)
mit den Parametern a und b des angepassten Polynoms. Die so bestimmten Werte für
−1
sind für die oben aufgeführte Messung in Abb. 5.7 mit blauen Kreisen markiert.
Rmin
Man sieht sofort, dass einige der so bestimmten Minima genau zwischen zwei gemessenen
Werte liegen.
Auf diese Weise muss das Minimum nicht direkt gemessen werden, sondern kann bei
−1
genügend vielen Messwerten extrapoliert werden. Da der Wert von Rmin
aus allen Mess-
werten gewonnen wird, ist die Bestimmung unabhängig von der Granularität der Korrektornetzgeräte. Allerdings begrenzt die Granularität der Netzgeräte die Anzahl der
−1
Messpunkte die aufgenommen werden können. Der Fehler von Rmin
resultiert aus dem
Fehler bei der Bestimmung der quadratischen Orbitabweichung. Diese ist nur von der Genauigkeit der Strahllagemonitore abhängig. Der statistische Fehler bei der Bestimmung
q
von xc skaliert dabei mit N 1−p , wobei N die Zahl der Messwerte und p die Anzahl der
zu bestimmender Parameter ist [5].
61
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
0.1
0.08
0.06
0.04
0.02
0
-3
-2
-1
K orrektor R
0
-1
0.04
0.02
0
-2.5
-2
-1.5
-1
K orrektor R -1 [m-1 ]
0.2
∆ k = -0.047 m-2
-0.5
x 10
-5
∆ k = -0.053 m-2
2
0.15
0.1
0.05
0
-0.05
-3.5
0.06
-5
quad. Orbitabw. [mm ]
quad. Orbitabw. [mm2 ]
x 10
∆ k = -0.041 m-2
0.08
-0.02
-3
1
-1
[m ]
0.2
-3
-2.5
-2
-1.5
-1
K orrektor R -1 [m-1 ]
0.15
quad. Orbitabw. [mm2 ]
0.1
∆ k = -0.035 m-2
quad. Orbitabw. [mm2 ]
quad. Orbitabw. [mm2 ]
0.12
-0.5
x 10
-5
0.15
0.1
0.05
0
-3.5
-3
-2.5
-2
-1.5
K orrektor R -1 [m-1 ]
-1
-0.5
x 10
-5
∆ k = -0.059 m-2
0.1
0.05
0
-0.05
-3.5
-3
-2.5
-2
-1.5
K orrektor R -1 [m-1 ]
-1
x 10
-5
Abbildung 5.7.: Gemessene Werte der quadratischen Orbitabweichung in Abhängigkeit
von der Korrektorstärke R−1 und angepasste Polynome 2. Ordnung. Der blaue Kreis
markiert jeweils das Minimum des angepassten Polynoms, der rote Kreis markiert den
jeweils kleinsten gemessenen Wert.
62
5.3. Korrektorbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
−1
Direkte Bestimmung der Korrektorstärke Rmin
aus den Messwerten
−1
In der Entwicklungsphase der Methode wurde auf die Bestimmung von Rmin
durch einen
−1
Fit 2. Ordnung verzichtet. Die Korrektorstärke Rmin
, bei der die Orbitabweichung mi-
nimal ist, wurde in dieser Phase direkt aus den aufgenommenen Messwerten ermittelt.
Dabei wurde jeweils die Korrektorstärke gesucht, bei der die gemessene Orbitabweichung
minimal ist. Dies sind die rot markierten Messwerte in Abb. 5.7. Man sieht sofort, dass
diese Messwerte nicht immer das Minimum des parabelförmigen Verlaufs darstellen. Da
die durchgeführten Korrekturen der Quadrupolfehlaufstellungen anhand der so gewonnenen Daten durchgeführt wurde, soll der entstandene zusätzliche Fehler kurz diskutiert
werden.
−1
Die Auflösung bei dieser Art der Bestimmung von Rmin
ist begrenzt durch die 12 Bit
Auflösung der DACs/ADCs der Korrektornetzgeräte. Dies limitiert die minimale Schrittweite bei der Variation des Korrektorstroms auf 4.8 mA. Der Fehler ist also maximal,
wenn das Minimum genau zwischen zwei mit den Netzgeräten setzbaren Stromwerten
liegt, er beträgt dann ±2.4 mA. Diese Granularität der Netzgeräte überträgt sich auf die
verschiedenen Dipolkorrektoren unterschiedlich, abhängig von der Länge und Bestromung
des Quadrupols auf dem der jeweilige Korrektor montiert ist. Es lässt sich aber festhalten, dass die Granularität der Korrektorstärken ∆R−1 bei DELTA im günstigsten Fall
bei ∆R−1 = 34·10−7 m−1 und im ungünstigsten Fall bei ∆R−1 = 58·10−7 m−1 liegt. Dies
−1
führt zu einem maximalen Fehler bei der Bestimmung Rmin
von sR−1 = 2.9 · 10−6 m−1 .
min
Der Fehler überträgt sich auf die Bestimmung von xc , skaliert dabei aber mit (∆k)−1 .
Bei sehr kleinen ∆k-Werten ist der Fehler bei der Bestimmung von xc groß und liegt bei
sxc ≈ 200 µm. Bei den im Rahmen dieser Arbeit durchgeführten Messungen beträgt der
Fehler durch die Granularität der Netzgeräte der Dipolkorrektoren ca. 100 µm.
−1
Vergleich der Methoden zur Bestimmung der Korrektorstärke Rmin
Die direkt aus den Messdaten und über einen Fit 2. Ordnung ermittelten Wertepaare
−1
(∆k,Rmin
) sind für die obige Messung in Abb. 5.8 dargestellt. Der Wert von xc wird
durch eine lineare Regressionrechnung der Wertepaare bestimmt. Die auf die direkte Art
gewonnenen Wertepaare zeigen einen Sprung zwischen zwei diskreten Korrektorstärken.
Dieser ist durch die Granularität der Netzgeräte zu erklären, da diese keine Zwischenwerte der Korrektorstärke erzeugen können. Die durch einen Fit 2. Ordnung ermittelten
−1
Wertepaare (∆k,Rmin
) zeigen einen deutlich lineareren Verlauf ohne diskrete Sprünge.
Der Fehler bei der linearen Regression wird so minimiert.
63
Kapitel 5. Diskussion und Analyse der verwendeten Messmethoden
K orrektor R -1 [m-1 ]
-1
x 10
-5
-1.2
-1.4
-1.6
F it
direkt
-1.8
-0.06
-0.055
-0.05
-0.045
-0.04
-0.035
-2
K as kade ∆K [m ]
−1
−1
Abbildung 5.8.: Korrektorstärke Rmin
als Funktion von ∆k. rot: Messwerte (∆k,Rmin
)
aus Abb. 5.7 und dazugehörige lineare Ausgleichsgerade. blau: Über einen Fit 2. Ordnung
−1
bestimmte Wertepaare (∆k,Rmin
) und dazugehörige lineare Ausgleichsgerade.
5.3.3. Genauigkeit
Die Abhängigkeit der Genauigkeit der korrektorbasierten Messmethode von der Art der
Auswertung wurde im vorangegangenen Abschnitt diskutiert. Zusätzlich hängt die Genauigkeit der bestimmten Quadrupolfehlaufstellung von der Genauigkeit der verwendeten
Systeme (Strahllagemonitore und Dipolkorrektoren) ab.
Der Elektronenstrahl muss durch die magnetischen Zentren der äußeren Triplettquadrupole geführt werden. Dazu werden die anliegenden Strahllagemonitore auf diese kalibriert. Der Fehler der Kalibrierung der Strahllagemonitore verschiebt die Achse des
Quadrupoltripletts, auf die sich die bestimmte Fehlaufstellung bezieht. Der Wert für xg
wird somit falsch bestimmt. Aus dem Fehler der Kalibrierung folgt für den Fehler von xg
sofort sxg ≤ (5 bis 100) µm, welcher sich wegen (4.28)
xoff = xg − xc
(5.16)
auf die bestimmte Fehlaufstellung überträgt.
Es wurden bei DELTA nur die Felder einiger Magnete exemplarisch vermessen. Bei
bekannter Bestromung der Korrektorspulen an einem langen Quadrupoljoch ist die Stärke
des entsprechenden Korrektorfeldes daher nur auf besser als 6 % genau bekannt [7]. Bei
−1
der Bestimmung von Rmin
wird daher ein systematischer Fehler von ≤ 6 % gemacht.
Somit muss auch für den bestimmten Wert der Strahlablage xc ein relativer Fehler von
6 % angegeben werden. Bei der im Rahmen dieser Arbeit durchgeführten Messungen
wurden nur Strahlablagen xc < 1000 µm gemessen. Aus dem relativen Fehler von 6 %
folgt ein absoluter Fehler von 60 µm. Auch dieser Fehler überträgt sich mit (4.28)
xoff = xg − xc
64
(5.17)
5.3. Korrektorbasierte Methode zur Bestimmung von Quadrupolfehlaufstellungen
auf die bestimmte Fehlaufstellung.
Da dies die beiden dominierenden Fehler bei dieser Methode sind, kann die Genauigkeit
der Bestimmung von der Quadrupolfehlaufstellung xoff mit ≤ (60 bis 117) µm angegeben
werden. Sind die Strahllagemonitore sehr genau kalibriert und ist die Strahlablage xc
sehr klein, so wird auch der Fehler der bestimmten Fehlaufstellung sehr klein.
65
6. Messergebnisse und Bewertung der
Messmethoden
Insgesamt sind im Speicherring DELTA 18 Quadrupoltripletts zur strahlbasierten Vermessung geeignet. Es wurden zunächst die Quadrupoltripletts strahlbasiert vermessen,
die einen Dipolkorrektor besitzen der stark belastet ist. Alle der so ausgewählten Quadrupole wiesen Fehlaufstellungen auf. Im Folgenden sollen die Ergebnisse der Vermessung
von zwei im Rahmen dieser Arbeit vermessenen Quadrupoltripletts exemplarisch präsentiert werden. Anschließend werden die Ergebnisse beider Methode miteinander verglichen. Ein weiterer Vergleich der Methoden erfolgt über die Genauigkeit der Bestimmung
der Strahlablage im mittleren Triplettquadrupol. Abschließend wird eine Bewertung der
Methoden durchgeführt.
Im Folgenden werden für die Ergebnisse der strahlbasierten Messungen nur die statistischen Fehler angegeben, hinzu kommt der systematische Fehler der jeweiligen Methode,
vgl. Kap. 5.2.4 und Kap. 5.3.3.
6.1. Iterative Anwendung der modellbasierten Methode am
Beispiel des Tripletts „qf03+06“
Als Erstes wurde das Quadrupoltriplett um den horizontal fokussierenden Quadrupol
„qf03+06“ strahlbasiert vermessen. Die Auswahl dieses Tripletts geschah aufgrund der
folgenden Kriterien:
• Der horizontale Dipolkorrektor „hk19“ auf dem Quadrupol „qf03+06“ war maximal
belastet, d.h. er wurde mit 10 A bestromt.
• Das Quadrupoltriplett befindet sich im südöstlichen Quadranten des Speicherrings
DELTA. Dort existierte bereits eine Datenanbindung zum Kontrollsystem für die
induktiven Wegaufnehmer. Die Überwachung und Protokollierung einer potentiellen Positionskorrektur der Quadrupole über das EPICS-Log (vgl. Kap 3.2.4) war
somit möglich.
67
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
• Das Triplett war bereits für eine geodätische Vermessung vorbereitet. Eine Positionskorrektur konnte ohne zusätzliche Vorbereitung auch geodätisch überwacht
werden.
An den äußeren Quadrupolen des Tripletts „qd04+11“ und „qd04+12“ befinden sich die
Strahllagemonitore „bpm34“ und „bpm35“. Diese wurden zunächst strahlbasiert auf die
magnetische Mitte des jeweiligen Quadrupols kalibriert.
Für die Vermessung des Tripletts wurde ein möglichst glatter Orbit ohne Orbitbeulen
eingestellt. Aufgrund der in Kap. 5.2.1 beschriebenen Einflüsse auf die Messung wurden
alle Sextupolmagnete und der horizontale Korrektor „hk19“ deaktiviert. Für die Messung
wurde der Strahl so geführt, dass er in den Strahllagemonitoren „bpm34“ und „bpm35“
keine Ablage mehr besaß. Danach wurde die Orbit- und Arbeitspunktkorrektur deaktiviert.
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,41
0,0243
2,937
-20,522
-1,795
-1,073
-0,152
0,722
0,42
0,0249
2,985
-21,438
-1,825
-1,090
-0,159
0,734
0,43
0,0255
2,990
-21,991
-1,828
-1,092
-0,163
0,735
0,44
0,0262
2,980
-22,586
-1,821
-1,088
-0,167
0,733
0,45
0,0268
2,971
-23,122
-1,816
-1,085
-0,171
0,731
0,46
0,0275
2,943
-23,565
-1,799
-1,075
-0,175
0,724
0,47
0,0280
2,966
-24,228
-1,813
-1,083
-0,180
0,729
0,48
0,0285
3,013
-25,072
-1,842
-1,101
-0,186
0,741
0,49
0,0292
3,007
-25,718
-1,838
-1,099
-0,191
0,740
Tabelle 6.1.: Ergebnisse der modellbasierten Vermessung des Quadrupoltripletts um
„qf03+06“ vor allen Positionskorrekturen bei verschiedenen ∆k-Strömen ∆i.
Die eigentliche Messung über die modellbasierte Methode gemäß Kap. 4.2.1, wurde
unter den Bedingungen des Maschinensetups „DELTA.090813-1500MeV-SAW-6.snap“ bei
einem Arbeitspunkt von νx = 9,128 und νy = 3,177 mit 10 unterschiedlichen ∆k-Werten
durchgeführt. Die verwendeten Parameter und Ergebnisse der einzelnen Messungen sind
in Tab. 6.1 und die statischen Parameter des Quadrupoltripletts, die zur Berechnung der
Fehlaufstellung nötig sind, sind in Tab. 6.2 aufgeführt.
Als Ergebnis ergibt sich als arithmetisches Mittel der Ergebnisse der Einzelmessungen
eine Fehlaufstellung des mittleren Triplettquadrupols „qf03+06“ von xoff = (732 ± 6) µm
zu der Achse der äußeren Quadrupole, wobei der angegebene Fehler nicht den systematischen Fehler der Messmethode berücksichtigt.
68
6.1. Iterative Anwendung der modellbasierten Methode am Triplett „qf03+06“
kqf03+06
=
−3,77 m−2
leff,qf03+06
=
0,434 m
s12
=
0,729 m
s23
=
0,732 m
Tabelle 6.2.: Parameter des Quadrupoltripletts „qf03+06“. Parameter: k: Fokussierstärke, leff : effektive Magnetlänge, s12,23 : Abstand zwischen 1. und 2. bzw 2. und 3. Quadrupol
des Tripletts
6.1.1. Iterative Korrektur der Fehlaufstellung
Die Korrektur der Quadrupolposition geschieht über dafür vorgesehene Stellschrauben,
die in der Stützstruktur integriert sind. Zur Überwachung der Positionskorrektur wurden
drei unabhängige Systeme verwendet. Auf der Außen- und Innenseite des Quadrupols
wurden induktive Wegaufnehmer auf Messsäulen installiert, die mittig an dem Quadrupoljoch angreifen. Die Wegaufnehmersignale wurden über das EPICS-Log ausgewertet
und protokolliert. Zusätzlich wurden auf der Stützstruktur Messuhren, die eine Genauigkeit von ±10 µm besitzen, installiert, die an die Außenseite der Füße des Quadrupols
angreifen. Außerdem wurde die Positionskorrektur geodätisch überwacht [1].
Erste Positionskorrektur
Da die mit der modellbasierten Methode bestimmten Fehlaufstellungen erfahrungsgemäß
zu groß sind wurde die strahlbasiert bestimmte Fehlaufstellung xoff = (−732 ± 6) µmin
einem ersten Schritt um ∆x = −400 µm korrigiert.
Bei der Korrektur der Quadrupolposition wurden die Daten der Messuhren als Referenzwert verwendet, da diese sofort vor Ort ohne weitere Auswertung verfügbar waren.
Der Quadrupol wurde entsprechend der Messuhren um ∆xµ-Uhr = (−400 ± 14) µm (nach
innen) bewegt. Nach diesem ersten Iterationsschritt wurde die strahlbasierte Vermessung
wiederholt. In der darauf folgenden Messreihe wurden 12 Einzelmessungen für verschiedene ∆k-Werte durchgeführt. Die Parameter und Ergebnisse der Einzelmessungen sind im
Anhang in den Tabellen A.2-A.3 aufgeführt. Daraus ergibt sich als arithmetisches Mittel
der Ergebnisse der Einzelmessungen eine Fehlaufstellung des mittleren Triplettquadrupols „qf03+06“ von xoff = (580 ± 30) µm. Die Auswertung der protokollierten Daten der
induktiven Wegaufnehmer, siehe Abb. 6.1, ergibt eine Verschiebung des Quadrupols von
∆xWegaufn. = (−430 ± 28) µm.
Die induktiven Wegaufnehmer und die Messuhren liefern im Mittel eine tatsächliche
Verschiebung des Quadrupols von ∆xreal = (−420 ± 20) µm. Strahlbasierte konnte nur
eine Verschiebung der Quadrupolposition von ∆xsb = (160 ± 40) µm beobachtet werden.
69
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
0.2
Wegaufnehmerpos ition [mm]
(aus s en)
0
dx= -0.434 mm
-0.2
-0.4
-0.6
dx = -0.574 mm
-0.8
-1
dx = -0.368 mm
-1.2
-1.4
16:00
18:00
20:00
22:00
00:00
02:00
04:00
06:00
Datum / Uhrzeit
08:00
10:00
12:00
14:00
16:00
Abbildung 6.1.: Zeitlicher Verlauf der Tastkopfposition des induktiven Wegaufnehmers,
der mittig an der Außenseite des Quadrupols angreift, zur Überwachung der Positionsanpassung des Quadrupols „qf03+06“. Die Daten zeigen den Zeitraum vom 13.08.09 16:00
Uhr bis 14.08.09 16:00 Uhr.
Dabei ist ∆xsb die Differenz der strahlbasiert bestimmten Fehlaufstellung des Quadrupols
vor (xoff1 ) und nach (xoff2 ) der Positionskorrektur gemäß
∆xsb = xoff2 − xoff1
(6.1)
In Folge der ersten Positionskorrektur konnte der horizontale Korrektor „hk19“ in seiner
Bestromung von 10 A auf 7.499 A entlastet werden.
Weitere Positionskorrekturen
Qualitativ ergab die geodätische Vermessung, dass der mittlere Quadrupol in Bezug auf
die Triplettachse nach der ersten Positionskorrektur weiterhin zu weit außen steht. Aufgrund dieses qualitativen Ergebnisses und des Ergebnisses der strahlbasierten Vermessung wurde beschlossen, die Position des Quadrupols „qf03+06“ nochmals zu korrigieren.
Dies geschah in 2 weiteren Schritten, nach denen jeweils eine weitere strahlbasierte Vermessung zur Kontrolle durchgeführt wurde. Bei der Positionskorrektur wurde wieder der
Messwert der Messuhren als Referenz verwendet. Die Messwerte der Messuhren, der induktiven Wegaufnehmer und der strahlbasierten Vermessung für alle Korrekturschritte
sind in Tab. 6.3 aufgeführt. Nach den drei Positionskorrekturen ergab die strahlbasierte
Vermessung eine verbleibende Fehlaufstellung von xoff = (10 ± 10) µm. Die verbleibende
Fehlaufstellung liegt deutlich unter der geforderten Genauigkeit der Quadrupolposition
70
6.1. Iterative Anwendung der modellbasierten Methode am Triplett „qf03+06“
Korrekturschritt
∆xMessuhr
∆xWegaufn.
∆xstrahlb.
1
(−400 ± 30) µm
(−430 ± 20) µm
(−160 ± 40) µm
2
(−600 ± 30) µm
(−570 ± 20) µm
(−370 ± 40) µm
3
(−320 ± 30) µm
(−370 ± 20) µm
(−190 ± 10) µm
Tabelle 6.3.: Messwerte der Quadrupolpositionsänderungen bestimmt mit Messuhren,
induktiven Wegaufnehmer und über die strahlbasierte Vermessung für alle drei Korrekturschritte.
von ±100 µm. Auch über die geodätische Vermessung konnte keine signifikante Fehlaufstellung mehr festgestellt werden. Daher wurde auf eine weitere Positionskorrektur
verzichtet. Die Bestromung des Dipolkorrektors „hk19“ konnte durch die zusätzlichen
Positionskorrekturen um weitere 5,5 A reduziert werden. Insgesamt konnte so die Bestromung von −10 A auf −2 A reduziert werden, vgl. Kap. 6.4.2.
6.1.2. Ergebnis
Durch die iterative Anwendung der modellbasierten Methode konnte die Quadrupolfehlaufstellung mit einer größeren als der geforderten Genauigkeit korrigiert werden. Auffällig
ist, dass die strahlbasiert gemessenen Positionsänderungen (siehe Tab. 6.3) um einen Faktor von 2,0-2,5 zu klein ausfällt. Auch die absolute Fehlaufstellung vor den Korrekturen
fiel mit xoff = (730±10) µm ebenfalls etwa um einen Faktor 2 kleiner aus, als die tatsächliche Fehlaufstellung von xoff,real = (1320 ± 30) µm. Betrachtet man die durch das ∆k
0.5
gemes s ene Orbitänderung
s imulierte Orbitänderung
0.4
0.3
Ablage [mm]
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4
0
5
10
15
20
25
30
35
40
45
50
55
60
65
P os ition [m]
70
75
80
85
90
95
100
105
110
115
Abbildung 6.2.: Gemessene und simulierte ∆k-Orbitänderung. Es zeigen sich zum Teil
deutliche Abweichungen.
verursachte gemessene Orbitänderung und dazu die simulierte Orbitänderung in Abb.
6.2, so fällt auf, dass diese an vielen Strahllagemonitoren ebenfalls eine Abweichung von
71
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
bis zu einem Faktor zwei aufweist. Dieser Faktor übertragt sich durch die Linearität
der Orbitstörung auf den durch das Verfahren bestimmten Ablenkwinkel des virtuellen
Dipolkorrektors und somit über (4.7) und (4.11) auch direkt auf die bestimmte Fehlaufstellung des Quadrupols. Die Genauigkeit des Modells limitiert somit die Genauigkeit
des Verfahrens.
6.1.3. Erster Test der korrektorbasierten Methode
Vor und nach der zweiten Positionskorrektur wurde erstmals das korrektorbasierte Messverfahren nach Kap. 6.2 getestet. Da sich die Methode in der Entwicklungsphase befand,
geschah die Bestimmung des minimalen Korrektorwertes direkt aus dem kleinsten gemessenen Wert der Orbitänderung und nicht über einen Fit 2. Ordnung. Die Genauigkeit bei
dieser Art der Bestimmung des Minimums ist, wie in Kap. 5.3.2 beschreiben, durch die
Auflösung der Netzgeräte limitiert. Vor der 2. Positionskorrektur konnte so eine Fehlaufstellung des Quadrupols „qf03+06“ von xoff,sb = (+760±40) µm als arithmetisches Mittel
mehrerer Messungen bestimmt werden. Nach der 2. Positionskorrektur wurde mit diesem
Messverfahren noch eine Fehlaufstellung von xoff = (+240±40) µm gemessen. In Tab. 6.4
Messmethode
∆x
Messuhren / ind. Wegaufnehmer
(−590 ± 30) µm
modellbasierte Methode
(−370 ± 40) µm
korrektorbasierte Methode
(−520 ± 60) µm
Tabelle 6.4.: Quadrupolpositionsänderung ∆x bestimmt mit Messuhren/induktiven Wegaufnehmer und mit modell- und korrektorbasierter Messmethode für die 2. Positionskorrektur.
sind die mit den 4 verwendeten Verfahren gemessenen Positionsänderungen der 2. Positionskorrektur gegenübergestellt. Ein Vergleich zeigt, dass die mit der korrektorbasierten
Messmethode bestimmte Positionsänderung im Rahmen der Fehlerintervalle verträglich
mit der real gemessenen Positionsänderung ist. Die Fehlaufstellung des Quadrupols wurde
somit deutlich präziser als mit der modellbasierten Messmethode bestimmt.
6.2. Anwendung der korrektorbasierten Methode am
Beispiel des Tripletts „qf03+02“
Eine weitere strahlbasierte Vermessung wurde am Quadrupoltriplett um den horizontal
fokussierenden Quadrupol „qf03+02“ durchgeführt, da hier ebenfalls der horizontale Dipolkorrektor „hk04“ mit −7.5 A stark belastet war. Die Vermessung wurde aufgrund der
72
6.2. Anwendung der korrektorbasierten Methode am Triplett „qf03+02“
Ergebnisse des Tripletts „qf03+06“ (vgl. Kap. 6.1.3) mit der korrektorbasierten Methode
durchgeführt. Um einen Vergleich der beiden strahlbasierten Messmethoden zu ermöglichen (siehe Kap. 6.3.1) wurde zusätzlich auch die modellbasierte Methode angewendet.
Das Triplett besteht aus dem mittleren horizontal fokussierenden Quadrupol „qf03+02“
und den äußeren horizontal defokussierenden Quadrupolen „qd04+03“ und „qd04+04“.
An diesen befinden sich die Strahllagemonitore „bpm07“ und „bpm08“. Diese wurden
analog zum voran gezeigten Beispiel zunächst strahlbasiert auf die magnetische Mitte
des anliegenden Quadrupols kalibriert.
Für die strahlbasierte Vermessung des Tripletts wurden, wie bei der Anwendung der
modellbasierten Messmethode am Triplett „qf03+06“, die folgenden Vorbereitungen getroffen:
• Ausschalten aller Sextupolmagnete und des horizontalen Dipolkorrektors „hk04“
• Entfernung aller Orbitbeulen und Erzeugung einer Ablage von 0 mm in den TriplettStrahllagemonitoren „bpm07“ und „bpm08“
• Deaktivierung der Orbit- und Arbeitspunktkorrektursoftware
Die Vermessung wurde mehrfach durchgeführt und die Fehlaufstellung als arithmetisches Mittel der Ergebnisse der Einzelmessungen ermittelt.
6.2.1. Korrektur der Fehlaufstellung
Die Messung wurde im Entwicklungsstadium der Methode durchgeführt, daher geschah
−1
die Korrektur der Fehlaufstellung anhand des Wertes Rmin
bei dem die kleinste Orbit-
abweichung gemessen wurde (vgl. Kap 5.3.2). Nachträglich wurden die Daten nochmals
mit einem Fit 2. Ordnung ausgewertet. Die Ergebnisse beider Auswertungen sind in Tab.
6.5 aufgeführt. Dabei ergab sich je nach Auswertungsmethode eine Fehlaufstellung von
xoff = +370 µm bis xoff = +390 µm.
Nach der ersten Positionskorrektur des Quadrupols um ∆x = (−460 ± 20) µm wurde
aufgrund eines Auswertungsfehlers weiterhin eine signifikante Fehlaufstellung festgestellt.
Daher wurde die Quadrupolposition ein zweites Mal um ∆x = (−290 ± 20) µm angepasst
und die anfängliche Fehlaufstellung somit überkompensiert. Die daraus resultierende neue
Fehlaufstellung von xoff = (−390 ± 200) µm wurde dann in einem dritten Schritt um
∆x = (+310 ± 20) µm korrigiert.
Die Strecke, um die der Quadrupol „qf03+02“ insgesamt verschoben wurde, ist größer
als die anfängliche strahlbasiert ermittelte Fehlaufstellung. Daher verblieb eine Fehlaufstellung von xoff = (−140 ± 40) µm, die noch zu korrigieren war. Aufgrund der Rahmen-
73
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
nach
Fehlaufstellung
Fehlaufstellung
Korrektur-
(direkt)
(Fit 2. Ordnung)
schritt
xoff [µm]
xoff [µm]
unkorrigiert
+390 ± 90
+370 ± 60
1
−130 ± 70
−100 ± 30
2
−390 ± 200
−410 ± 10
3
−90 ± 180
−140 ± 40
Tabelle 6.5.: Ergebnisse der korrektorbasierten Vermessung der Fehlaufstellung des Quadrupols „qf03+02“ vor und nach den drei Positionskorrekturen.
bedingungen des DELTA Strahlbetriebs steht die Korrektur der verbliebenen Fehlaufstellung noch aus.
In Tab. 6.6 sind die Positionsänderungen des Quadrupols zwischen den einzelnen Korrekturschritten aufgeführt. Die strahlbasiert bestimmten Positionsänderungen ergeben
sich dabei aus den gemessenen Fehlaufstellungen vor und nach dem jeweiligen Korrekturschritt (vgl. Tab. 6.5). Die strahlbasiert bestimmte anfängliche Fehlaufstellung des
∆xreal
∆xstrahlb.
∆xstrahlb.
Positions-
Messuhr/Wegaufnehmer
korrektorbasiert
korrektorbasiert
korrektur
[µm]
(direkt) [µm]
(Fit 2. Ordnung) [mm]
1
−460 ± 20
−512 ± 110
−470 ± 70
2
−290 ± 20
−258 ± 210
−300 ± 30
3
+300 ± 20
+300 ± 270
+270 ± 40
Summe
−450 ± 30
−470 ± 360
−500 ± 80
Tabelle
6.6.:
Gemessene
Quadrupolpositionsänderung
∆x
bestimmt
mit
Messuhren/induktiven Wegaufnehmer und über die strahlbasierten Vermessung für
die drei einzelnen Positionskorrekturen und die gesamte Positionskorrektur. Der Fehler
der Summe ergibt sich aus dem Gauß’schen Fehlerfortpflanzungsgesetz [5]
Quadrupols von xoff,Anfang = (+370 ± 60) µm wurde insgesamt um ∆xreal = (−450 ±
30) µm korrigiert. Mit der korrektorbasierten Messmethode konnte strahlbasiert eine
Änderung der Quadrupolposition um ∆xstrahlb. = (−500 ± 80) µm beobachtet werden.
Aus den Werten der anfänglichen Fehlaufstellung xoff,Anfang und der gemessenen Positionsänderung ∆xreal ergibt sich, dass nach der Korrektur eine Fehlaufstellung von
xoff,theo = −80 µm verbleiben sollte. Strahlbasiert konnte die verbleibende Fehlaufstellung zu xoff = (−140 ± 40) µm bestimmt werden.
74
6.3. Vergleich der Messmethoden
6.2.2. Ergebnis
Es zeigt sich, dass die korrektorbasierte Messmethode dazu geeignet ist, die Fehlaufstellung des mittleren Triplettquadrupols im Rahmen der geforderten Genauigkeit zu
bestimmen. Die real gemessene Positionsänderung des Quadrupols konnte strahlbasiert
mit einer Genauigkeit von deutlich unter 100 µm reproduziert werden. Insgesamt ermöglicht das korrektorbasierte Messverfahren eine Korrektur der Fehlaufstellung in einem
einzelnen Schritt. Der Dipolkorrektor „hk04“ konnte durch die Positionskorrektur des
Quadrupols von −7,5 A um 4 A auf −3,5 A entlastet werden.
6.3. Vergleich der Messmethoden
6.3.1. Genauigkeit der Bestimmung der Fehlaufstellung
Bei der in Kap. 6.2 präsentierten Vermessung der Fehlaufstellung des Quadrupoltripletts
„qf03+02“ wurden beide strahlbasierten Messmethoden angewendet. Um einen Vergleich
zu ermöglichen, wurde die Fehlaufstellung vor und nach jeder Positionskorrektur sowohl
mit der korrektorbasierten als auch mit der modellbasierten Methode gemessen. Die mit
beiden Methoden gemessenen Werte der Fehlaufstellung xoff vor den jeweiligen Positionskorrekturen sind in Tabelle 6.7 aufgeführt. Der direkte Vergleich zeigt, dass die mit
der modellbasierten Methode gemessenen Werte meist deutlich größer ausfallen als die
mit der korrektorbasierten Methode gemessenen
Positions-
xoff [µm]
xoff [µm]
korrektur
korrektorbasiert
modellbasiert
unkorrigiert
+370 ± 60
+610 ± 10
1
−100 ± 30
−120 ± 10
2
−410 ± 10
−770 ± 10
3
−140 ± 40
—
Tabelle 6.7.: Messwerte der Fehlaufstellung xoff des Tripletts „qf03+02“ gemessen mit
beiden Messmethoden vor und nach den jeweiligen Positionskorrekturen (vgl. Kap 6.2).
Die Differenz der strahlbasiert gemessenen Fehlaufstellung vor und nach einer Positionskorrektur ∆xsb. sollte im Idealfall der mit den Messuhren/Wegaufnehmern gemessenen Positionsänderung ∆xreal des Quadrupols entsprechen. In Tabelle 6.8 sind die entsprechenden Werte ∆x für die erste und zweite Positionskorrektur gegenübergestellt. Es
zeigt sich eine sehr gute Übereinstimmung der realen Positionsänderungen mit der Positionsänderung, die mit der korrektorbasierten Methode bestimmt wurde. Die mit der
75
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
Positions-
∆xreal [µm]
∆xsb. [µm]
∆xsb. [µm]
korrektur
Messuhr/Wegaufnehmer
korrektorbasiert
modellbasiert
1
−460 ± 20
−470 ± 70
−730 ± 10
2
−290 ± 20
−300 ± 30
−640 ± 1
Tabelle 6.8.: Positionsänderung ∆x des Quadrupols „qf03+02“ bei der Korrektur der
Fehlaufstellung (vgl. Kap 6.2).
modellbasierten Methode bestimmten Werte der Positionsänderung sind um etwa einen
Faktor zwei größer, da im Modell die Sextupolfelder der Dipolkorrektoren nicht korrekt
erfasst werden und die Teilchenbahn somit nicht richtig simuliert wird.
6.3.2. Genauigkeit der Bestimmung von xc
Den Kern der beiden strahlbasierten Messmethoden zur Bestimmung von Quadrupolfehlaufstellungen bildet die Bestimmung der Ablage xc des Strahls in Bezug auf die magnetische Achse des mittleren Triplettquadrupols. Diese ist im Allgemeinen unbekannt,
da die DELTA-Tripletts standardmäßig nur mit zwei Strahllagemonitoren an den äußeren Quadrupolen ausgestattet sind. Zwei der DELTA-Tripletts sind jedoch mit drei statt
zwei Strahllagemonitoren ausgestattet, so dass sich an jedem Quadrupol des Tripletts
ein solcher befindet. Die Strahlablage ist hier also in allen Triplettquadrupolen jederzeit bekannt. Eines dieser Tripletts befindet sich im Injektionsbereich und ein weiteres
am DELTA-Cavity. An diesen beiden Tripletts ist es möglich die durch die strahlbasierten Methoden bestimmte Strahlposition xc im mittleren Quadrupol mit den Daten der
Strahllagemonitore zu vergleichen.
Eine solche Vergleichsmessung wurde am Triplett um den Quadrupol „qf01+01“, welches sich im Bereich des DELTA-Cavities befindet, durchgeführt. Alle drei Strahllagemonitore wurden dazu auf die Achse des jeweiligen Quadrupols kalibriert. Die Strahllagemonitore „bpm54“ und „bpm02“ befinden sich an den Außenseiten des Tripletts. Der
Monitor „bpm01“ befindet sich direkt hinter dem mittleren Quadrupol „qf01+01“ und
dient im Folgenden der Kontrolle der Methoden.
Modellbasierte Messmethode
Die Messung mit der modellbasierten Messmethode wurde mit einem ∆k-Zusatzstrom
von I∆k = 0.42 A durchgeführt. Als Ergebnis der Messung wurde die Fehlaufstellung des
Quadrupols „qf01+01“ zu xoff,modell = −358 µm bestimmt. Eine spätere Korrektur der
Quadrupolposition zeigte, dass die reale Fehlaufstellung etwa xoff,real = (−300 ± 20) µm
betrug. Der Wert von xoff,real ergibt sich dabei aus der Differenz der Wegaufnehmerpositi-
76
6.3. Vergleich der Messmethoden
on vor und nach der Korrektur. Durch die modellbasierte Messung wurde die Strahlablage
im Quadrupol „qf01+01“ in Bezug auf dessen magnetische Achse zu xc,sb,modell = 1.24 mm
bestimmt. Die Kontrollmessung mit dem Strahllagemonitor „bpm01“ ergab, dass die tatsächliche Strahlablage xc,BPM = 1.38 mm betrug. Die relative Abweichung beträgt somit
11.3 %. Bei dieser Messung trat der häufig beobachtete Faktor zwei zwischen gemessener
und realer Fehlaufstellung nicht auf.
Mit einem zeitlichen Abstand von einigen Wochen wurde die Messung erneut durchgeführt. Die Fehlaufstellung wurde mit I∆k = 0.46 A strahlbasiert zu xoff = −187 µm
bestimmt, wobei die reale Fehlaufstellung weiterhin xoff,real = (−300 ± 20) µm betrug.
Auch eine Wiederholung mit anderen Kaskadenströmen brachte keine Verbesserung. Die
Strahlablage im Quadrupol „qf01+01“ in Bezug auf dessen magnetische Achse wurde zu
xc,sb,modell = 641 µm bestimmt. Mit dem Strahllagemonitor „bpm01“ wurde die Strahlablage zu xc,BPM = 924 µm bestimmt. Es zeigt sich eine deutliche Abweichung des strahlbasiert gemessenen Wertes von dem mit dem Strahllagemonitor aufgezeichneten Wert.
Korrektorbasierte Messmethode
Die einzelnen Messschritte der korrektorbasierten Messung sind in Abbildung 6.3 dargestellt. Die Messung wurde für ∆k-Zusatzströme I∆k = −0,5 bis −1,0 A durchgeführt. Dabei ergab sich eine Fehlaufstellung des Quadrupols „qf01+01“ von xoff,korrektor = −317 µm
bei einer realen Fehlaufstellung von xoff,real = (−300 ± 20) µm.
Mehrere Kontrollmessungen wurden am Triplett „qf01+01“ durchgeführt. Mit der korrektorbasierten Messmethode wurde eine Strahlablage von xc,sb. = (957 ± 49) µm im
mittleren Quadrupol gemessen. Der zuvor auf die magnetische Mitte des Quadrupols
kalibrierte Strahllagemonitor „bpm01“ hat die Strahlablage zu xc,BPM = (917 ± 5) µm
bestimmt. Die relative Abweichung beträgt somit 4,4 %.
Mit einem zeitlichen Abstand von einigen Wochen wurde auch diese Messung erneut
durchgeführt. Die Fehlaufstellung wurde strahlbasiert zu xoff,korrektor = −302 µm bestimmt, wobei die reale Fehlaufstellung weiterhin xoff,real = (−300 ± 20) µm betrug.
Die Strahlablage im Quadrupol „qf01+01“ in Bezug auf dessen magnetische Achse wurde
zu xc,sb,korrektor = (910 ± 50) µm bestimmt. Mit dem Strahllagemonitor „bpm01“ wurde
die Strahlablage zu xc,BPM = 902 µm bestimmt.
Die korrektorbasierte Messmethode bestimmt reproduzierbar mit hoher Genauigkeit
die Strahlablage im mittleren Triplettquadrupol und in Folge dessen auch die Fehlaufstellung des Quadrupols in Bezug auf die Triplettachse.
77
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
12
-2
quad. Orbitabw. [mm2 ]
∆ k = -0.035 m
2
quad. Orbitabw. [mm ]
4
3
2
1
0
-10
-5
0
10
5
-0.5
0
K orrektor R
quad. Orbitabw. [mm2 ]
30
4
2
25
-2
-1
6
0.5
-1
1
-1
[m ]
1.5
x 10
-1
-4
-0.5
0
0.5
1
K orrektor R -1 [m-1 ]
∆ k = -0.047 m
0
-1.5
8
-5
quad. Orbitabw. [mm2 ]
quad. Orbitabw. [mm2 ]
15
x 10
10
0
-1.5
5
K orrektor R -1 [m-1 ]
-2
∆ k = -0.041 m
1.5
x 10
-4
-2
∆ k = -0.053 m
20
15
10
5
0
-1.5
-1
-0.5
0
0.5
K orrektor R -1 [m-1 ]
1
1.5
x 10
-4
-2
∆ k = -0.059 m
25
20
15
10
5
0
-1.5
-1
-0.5
0
0.5
K orrektor R -1 [m-1 ]
1
1.5
x 10
-4
Abbildung 6.3.: Korrektorbasierte Messmethode: Gemessene Werte der quadratischen
Orbitabweichung in Abhängigkeit von der Korrektorstärke R−1 für verschiedene ∆kWerte.
78
6.4. Auswirkung der Korrektur der Fehlaufstellungen
6.4. Auswirkung der Korrektur der Fehlaufstellungen
6.4.1. Reduktion der integralen Korrektorstärke
Die Fehlaufstellungen der DELTA Quadrupole führen dazu, dass ein Strahlbetrieb ohne
Dipolkorrektoren nicht möglich ist, da die Summe der Orbitstörungen durch die einzelnen
Fehlaufstellungen zu zu großen Strahlablagen führen. Die Dipolkorrektoren werden somit
zu einem großen Teil zur Kompensation der Orbitstörungen durch die Fehlaufstellungen
verwendet. Eine Reduktion der Anzahl und Stärke der Quadrupolfehlaufstellungen sollte
somit zu einer Reduktion der Belastung der Dipolkorrektoren führen. Die Gesamtbelastung der Dipolkorrektoren lässt sich durch die integrale Korrektorstärke Θint. beschreiben
Θint. =
NX
Korr.
|Θi |
(6.2)
i=1
dabei ist NKorr. die Gesamtzahl der Korrektoren in der betrachteten Ebene und Θi der
Ablenkwinkel des Korrektors i. Bei der Korrektur der Fehlaufstellung des Quadrupols
2.7
2.68
integrale K orrektors täa rke [mrad]
2.66
2.64
2.62
2.6
2.58
2.56
2.54
2.52
2.5
-1.4
-1.2
-1
-0.8
-0.6
-0.4
F ehlaufs tellung [mm]
-0.2
0
Abbildung 6.4.: Integrale Korrektorstärke in Abhängigkeit von der Fehlaufstellung des
Quadrupols „qf03+06“.
„qf03+06“, vergleiche Kap. 6.1, wurde nach jedem Korrekturschritt bei gleichem Orbit
die integrale Korrektorstärke berechnet. Die ermittelten Werte für die horizontale Ebene
sind in Abhängigkeit von der Fehlaufstellung des Quadrupols in Abb. 6.4 dargestellt.
79
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
Wie erwartet sinkt die integrale Korrektorstärke mit der Reduktion der Fehlaufstellung
des Quadrupols „qf03+06“ von 2,662 mrad auf 2,511 mrad. Das entspricht einer Reduktion
der integralen Korrektorstärke von 5,7 %.
6.4.2. Lokalität der Korrektorentlastung
Die integrale Korrektorstärke gibt keine Auskunft darüber, ob die Entlastung der Korrektoren lokal geschieht oder ob mehrere Korrektoren entlastet werden. In Kap. 3.3.4
wurde die Hypothese aufgestellt, dass ein einzelner lokal stark belasteter Dipolkorrektor
hauptsächlich zur Kompensation der Orbitstörung verwendet wird, die durch die Fehlaufstellung des Quadrupols entsteht, auf dem dieser montiert ist. Die Auswahl des Quadru-
Korrektorstrom I [A]
10
5
0
-5
-10
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Nummer des horizontalen Korrektors
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Nummer des horizontalen K orrektors
K orrektors trom I [A]
10
5
0
-5
-10
Abbildung 6.5.: Bestromung der horizontalen Dipolkorrektoren Oben: vor der Korrektur der Fehlaufstellung des Quadrupols „qf03+06“. Unten: nach der Korrektur.
poltripletts „qf03+06“ zur strahlbasierten Vermessung (vgl. Kap. 6.1) geschah aufgrund
dieser Hypothese. In Abb. 6.5 ist die Konfiguration der Bestromung der horizontalen
Dipolkorrektoren vor und nach der Korrektur des Quadrupols „qf03+06“ dargestellt.
Der horizontale Dipolkorrektor „hk19“ befindet sich auf dem Quadrupol „qf03+06“ und
ist vor der Korrektur der Fehlaufstellung, mit −10 A, maximal belastet ist. Durch die
Korrektur der Fehlaufstellung ändert sich die Konfiguration der Bestromung der Dipol-
80
6.4. Auswirkung der Korrektur der Fehlaufstellungen
Anderung der
K orrektorbes tromung ∆ I [A]
korrektoren, siehe Abb. 6.6. Dabei ist zu beobachten, dass sich im Wesentlichen nur die
10
8
6
4
2
0
-2
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Nummer des horizontalen K orrektors
Abbildung 6.6.: Änderung der Bestromung der horizontalen Dipolkorrektoren aufgrund
der Korrektur der Fehlaufstellung des Quadrupols „qf03+06“.
Bestromung des Korrektors „hk19“ ändert. Dieser konnte von −10 A um +8 A auf −2 A
entlastet werden. Alle anderen Korrektoren blieben in ihrer Bestromung fast unverändert. Dies zeigt, dass die hohe Belastung des Korrektors „hk19“ vor der Korrektur der
Fehlaufstellung des Quadrupols „qf03+06“ hauptsächlich der Kompensation der durch
die Fehlaufstellung verursachten Orbitstörung zuzuschreiben ist.
Lokal stark belastete Dipolkorrektoren sind bei DELTA somit ein Indiz für eine starke
Fehlaufstellung des Quadrupols auf dem der jeweilige Korrektor montiert ist. Im Prinzip
könnte auch ein benachbarter defokussierender Quadrupol eine Fehlaufstellung aufweisen,
die durch den betreffenden Dipolkorrektor ausgeglichen wird. Allerdings ist die Stärke
der Closed-Orbit-Störung durch eine Quadrupolfehlaufstellung nach (2.27) abhängig von
p
β(s) am Ort der Störung. Die horizontale Betafunktion β(s) in den defokussierenden
Quadrupolen beträgt aber nur etwa
1
11
der horizontalen Betafunktion in den fokussieren-
den Quadrupolen. Die Fehlaufstellung eines defokussierenden Quadrupols müsste somit
√
um 11 ≈ 3,3 größer sein, um die äquivalente Wirkung eines fehlaufgestellten fokussierenden Quadrupols zu erzeugen.
81
Kapitel 6. Messergebnisse und Bewertung der Messmethoden
6.5. Bewertung der Messmethoden
Die bisher verwendete modellbasierte Messmethode zur Bestimmung und Korrektur der
Fehlaufstellung von Triplettquadrupolen ist prinzipiell in der Lage die Quadrupolfehlaufstellungen mit ausreichend hoher Genauigkeit zu bestimmen. Im Speziellen zeigten sich
bei der Anwendung an DELTA jedoch Abweichungen der gemessenen Fehlaufstellungen
von den tatsächlichen Fehlaufstellungen der Quadrupole. Die strahlbasiert bestimmten
Werte sind zum Teil um einen Faktor zwei zu groß im Vergleich zu den real gemessenen.
Im Rahmen dieser Arbeit konnte der störende Einfluss der internen/externen Sextupolmagnete identifiziert und eliminiert werden. Es verbleiben allerdings die höheren
Multipolkomponenten der Dipolkorrektoren, die nicht beseitigt werden können. Der dominierende Fehler bei der Bestimmung der Fehlaufstellung resultiert jedoch aus der
Diskrepanz zwischen Modell und Realität. Mangels eines akkuraten Optik-Modells des
DELTA-Speicherrings konnte die modellbasierte Messmethode zwar, durch Elimination
der internen/externen Sextupole als Störquelle, in der Genauigkeit verbessert werden, ist
aber weiterhin nur iterativ anwendbar.
Die im Rahmen dieser Arbeit bei DELTA neu eingeführte korrektorbasierte Messmethode zeichnete sich bereits im Entwicklungsstadium durch eine deutlich höhere Genauigkeit und Zuverlässigkeit aus, da die Bestimmung der Fehlaufstellung ausschließlich
aus Messdaten erfolgt und keine Simulationsdaten nötig sind. Im Laufe der Entwicklung
konnte die Genauigkeit der Methode durch Anwendung eines Fits 2. Ordnung bei der
−1
Bestimmung von Rmin
sogar noch erhöht werden. Die Strahllage xc im mittleren Quadru-
pol konnte mit dieser Methode reproduzierbar mit einer relativen Genauigkeit von 4,4 %
bestimmt werden. Dies liegt im Bereich der Ungenauigkeit der Magnetfelder der Dipolkorrektoren, welche den limitierenden Faktor der Genauigkeit bei der Anwendung an
DELTA darstellen. Die Granularität der Netzgeräte der Dipolkorrektoren limitiert zwar
die Anzahl der möglichen Messpunkte, ist bei DELTA allerdings klein genug um eine
ausreichende Anzahl an Messpunkten aufzunehmen. Die statistische Schwankung der gemessenen Fehlaufstellungen ist ≤ 60 µm. Die Korrektur einer mit der korrektorbasierten
Methode festgestellten Fehlaufstellung kann daher in einem Schritt durchgeführt werden.
Eine iterative Anwendung der Methode ist nicht notwendig.
Daher ist der korrektorbasierten Methode der Vorzug zu geben, da die Fehlaufstellung
zuverlässig auf 6 % genau ist, bedingt durch die Limitierung der Genauigkeit der Dipolkorrektorfelder. Daher muss sie nicht iterativ angewendet werden. Der Arbeitsaufwand
wird so bei höherer Genauigkeit deutlich reduziert.
82
7. Zusammenfassung
Aufgrund von thermischen Effekten können sich die Quadrupole des DELTA Speicherrings von ihren Sollpositionen entfernen. Aus diesem Grund müssen die Positionen der
Quadrupole bestimmt und gegebenenfalls korrigiert werden. Zur Vermessung der Magnetpositionen werden neben geodätischen auch strahlbasierte Messmethoden verwendet, da
letztere auch unter den Bedingungen des Strahlbetriebs eingesetzt werden können. Diese
strahlbasierten Methoden wurden im Rahmen der vorliegenden Arbeit zur Bestimmung
und Korrektur der Fehlaufstellungen von Triplettquadrupolen benutzt.
Ein Ziel dieser Arbeit war zunächst die Untersuchung der bei DELTA bereits angewendeten strahlbasierten, iterativen Methode zur Bestimmung und Korrektur der Quadrupolfehlaufstellungen auf Störeinflüsse. Diese Methode basiert auf der Simulation der
am Speicherring gemessenen Orbitantwort auf eine ∆k-Störung der Quadrupolstärke
des mittleren Triplettquadrupols in einem MATLAB-Modell des Speicherrings. Aus den
Simulationsdaten lässt sich die Strahlposition im mittleren Quadrupol eines Tripletts bezüglich seiner magnetischen Achse bestimmen. Daraus ergibt sich seine Fehlaufstellung
bezüglich der Achse, die durch die magnetischen Mitten der äußeren Triplettquadrupole
definiert wird.
Zunächst wurde festgestellt, dass die Orbitantwort auf eine lineare ∆k-Störung ein
nichtlineares Verhalten aufweist. Als Grund dafür konnten die nichtlinearen Magnetfelder
im Speicherring, insbesondere die der internen und externen Sextupolmagnete identifiziert werden. Ein Abschalten der Sextupolmagnete reduzierte, wie erwartet, die Stärke
der Nichtlinearität der Orbitantwort. Zusätzlich weisen die Felder der Dipolkorrektoren,
bedingt durch ihre Bauweise, ebenfalls starke Sextupolkomponenten auf. Sie leisten einen
weiteren großen Beitrag zu den nichtlinearen Feldern im Speicherring. Aufgrund der globalen Fehlaufstellungen der DELTA Quadrupole können die Dipolkorrektoren und damit
die von ihnen erzeugten Sextupolfelder nicht ausgeschaltet werden. Aus diesem Grund
konnte die Nichtlinearität der Orbitantwort durch das alleinige Abschalten der internen
und externen Sextupolmagnete nur etwa auf die Hälfte reduziert werden.
Die Nichtlinearität der Orbitantwort wird im zugrunde liegenden MATLAB-Modell
nicht korrekt simuliert, da zum einen die Orbitantwort in nichtlinearen Feldern abhängig
83
Kapitel 7. Zusammenfassung
von der absoluten Strahlablage ist und zum anderen das Modell mit Designwerten der
Magnetstärken und Positionen arbeitet. Die Sextupolfelder der Dipolkorrektoren werden
im Modell überhaupt nicht erfasst. Die simulierte Orbitantwort zeigt aufgrund dessen
starke Abweichungen von der des realen Speicherrings und liefert bei der weiteren Rechnung nur einen Näherungswert der Fehlaufstellung.
Die modellbasierte Methode zeigte daher, abhängig vom betrachteten Triplett, uneinheitliche Fehler bei der Bestimmung der Fehlaufstellung. Bei der Bestimmung der
Strahlposition xc im mittleren Quadrupol des Tripletts „qf01+01“ trat nur ein relativer
Fehler von 11,3 % gegenüber dem direkt bestimmten Wert auf und der relative Fehler der
realen Fehlaufstellung betrug 18,5 %. An anderer Stelle („qf03-06“) konnte aber die reale
Fehlaufstellung nur mit einem relativen Fehler von 60 % bestimmt werden. Die großen
Fehler, die ihre Ursache in der ungenauen Kenntnis des optischen Modells haben, erlauben daher nur eine iterative Bestimmung von Fehlaufstellungen. Im Rahmen der Arbeit
konnten aber die Fehler gegenüber Messungen der Vergangenheit insgesamt deutlich verkleinert und die Anzahl der notwendigen Iterationen reduziert werden.
Im Rahmen dieser Arbeit wurde bei DELTA daher eine alternative Messmethode entwickelt. Die Orbitantwort des Speicherrings auf eine ∆k-Störung wird bei dieser Methode
durch ein ihr entgegengesetztes Dipolfeld kompensiert. Aus der zusätzlichen Quadrupolstärke ∆k und der zur Kompensation eingesetzten Dipolstärke R−1 lässt sich die
Strahlposition im mittleren Triplettquadrupol bestimmen. Daraus ergibt sich dann seine
Fehlaufstellung in Bezug auf die Triplettachse.
Die neu eingeführte korrektorbasierte Methode kommt im Gegensatz zur bisher verwendeten Methode ganz ohne Modellannahmen aus und ist daher mit deutlich geringeren
Fehlern bei der Bestimmung der Fehlaufstellung behaftet. Hier konnte die Strahlposition im Quadrupol „qf01+01“ mit einem relativen Fehler von nur 4,4 % und die reale
Fehlaufstellung mit nur 5 % ermittelt werden. Die Fehlerreduktion gegenüber der modellabhängigen Methode lag in diesem speziellen Fall bei ungefähr einem Faktor drei.
Messungen an anderen Tripletts zeigten dagegen eine deutlich größere Reduktion der
Fehler. Insgesamt konnten mit der neuen Methode Fehlaufstellungen mit einer absoluten Genauigkeit von (60 − 117) µm bestimmt werden. Dies ermöglicht die Korrektur der
Quadrupolfehlaufstellung in nur einem Schritt.
Für die Anwendung beider Messmethoden müssen die Strahllagemonitore auf die magnetischen Achsen der anliegenden Quadrupole kalibriert werden. Dazu wurde ebenfalls
eine strahlbasierte Methode eingesetzt. Es wurde dabei erstmals beobachtet, dass die
Dipolkorrektoren, die auf den Quadrupolen montiert sind, deren magnetische Achse für
84
die Kalibration der Strahllagemonitore herangezogen wird, die Messmethode stark beeinflussen. Eine genauere Untersuchung ergab aber, dass der Einfluss vernachlässigt werden
kann, wenn der Dipolkorrektor während der Messung in seiner Stärke nicht verändert
wird.
Basierend auf den Ergebnissen der vorliegenden Arbeit werden im DELTA-Speicherring
zunächst alle Quadrupol-Tripletts bezüglich ihrer internen Fehlaufstellung korrigiert. Die
Messprinzipien lassen sich im Prinzip auf benachbarte Tripletts und die Korrektur der
Aufstellung relativ zueinander erweitern. Sukzessive könnten so auch größere Abschnitte
im Ring relativ zueinander vermessen und bezüglich der Lage korrigiert werden. Dies
wird jedoch nicht ganz ohne Modellannahmen möglich sein.
85
A. Messergebnisse der modellbasierten
Methode
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,41
0,0243
2,937
-20,522
-1,795
-1,073
-0,152
0,722
0,42
0,0249
2,985
-21,438
-1,825
-1,090
-0,159
0,734
0,43
0,0255
2,990
-21,991
-1,828
-1,092
-0,163
0,735
0,44
0,0262
2,980
-22,586
-1,821
-1,088
-0,167
0,733
0,45
0,0268
2,971
-23,122
-1,816
-1,085
-0,171
0,731
0,46
0,0275
2,943
-23,565
-1,799
-1,075
-0,175
0,724
0,47
0,0280
2,966
-24,228
-1,813
-1,083
-0,180
0,729
0,48
0,0285
3,013
-25,072
-1,842
-1,101
-0,186
0,741
0,49
0,0292
3,007
-25,718
-1,838
-1,099
-0,191
0,740
Tabelle A.1.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 13.08.09
vor allen Positionskorrekturen.
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,40
0,0237
1,977
-13,458
-1,209
-0,722
-0,100
0,487
0,42
0,0251
2,432
-17,622
-1,488
-0,888
-0,130
0,599
0,44
0,0264
2,442
-18,658
-1,493
-0,892
-0,138
0,602
0,46
0,0274
2,500
-19,965
-1,529
-0,913
-0,148
0,616
0,48
0,0287
2,517
-21,111
-1,540
-0,920
-0,156
0,620
Tabelle A.2.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 13.08.09
nach der ersten Positionskorrektur um −400 µm.
87
Anhang A. Messergebnisse der modellbasierten Methode
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,43
0,0256
2,321
-17,177
-1,420
-0,848
-0,127
0,572
0,46
0,0275
2,326
-18,601
-1,422
-0,849
-0,138
0,573
0,49
0,0291
2,322
-19,770
-1,420
-0,848
-0,146
0,572
0,52
0,0310
2,299
-21,022
-1,406
-0,840
-0,156
0,566
0,55
0,0327
2,317
-22,448
-1,417
-0,846
-0,166
0,571
0,58
0,0347
2,327
-24,123
-1,423
-0,850
-0,179
0,573
0,61
0,0364
2,322
-25,380
-1,420
-0,848
-0,188
0,572
Tabelle A.3.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 13.08.09
nach der ersten Positionskorrektur um −400 µm.
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,46
0,0271
0,772
-6,058
-0,470
-0,282
-0,045
0,188
0,52
0,0305
0,851
-7,611
-0,518
-0,311
-0,056
0,207
0,58
0,0343
0,829
-8,436
-0,504
-0,303
-0,062
0,202
0,64
0,0377
0,896
-10,161
-0,545
-0,327
-0,075
0,218
Tabelle A.4.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 13.08.09
nach der zweiten und dritten Positionskorrektur um insgesamt weitere −600 µm.
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,40
0,0237
0,717
-4,851
-0,436
-0,262
-0,036
0,174
0,41
0,0241
0,859
-5,926
-0,523
-0,314
-0,044
0,209
0,42
0,0247
0,873
-6,180
-0,531
-0,319
-0,046
0,213
0,43
0,0254
0,823
-6,004
-0,501
-0,300
-0,044
0,200
0,44
0,0257
0,861
-6,372
-0,524
-0,315
-0,047
0,210
0,45
0,0264
0,874
-6,673
-0,532
-0,319
-0,049
0,213
0,46
0,0270
0,836
-6,516
-0,509
-0,305
-0,048
0,204
0,47
0,0277
0,829
-6,645
-0,504
-0,303
-0,049
0,202
0,48
0,0281
0,856
-6,988
-0,521
-0,313
-0,052
0,208
Tabelle A.5.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 13.08.09
nach der zweiten und dritten Positionskorrektur um insgesamt weitere −600 µm.
88
∆i [A]
∆k [ m12 ]
Θ [mrad]
∆Θ [µrad]
xc [mm]
x [mm]
∆xc [mm]
xoff [mm]
0,54
0,0316
0,060
-0,551
-0,036
-0,022
-0,004
0,014
0,58
0,0340
0,051
-0,513
-0,031
-0,019
-0,004
0,012
0,62
0,0362
0,060
-0,651
-0,037
-0,022
-0,005
0,015
0,66
0,0385
0,048
-0,560
-0,029
-0,018
-0,004
0,012
Tabelle A.6.: Messung am Quadrupoltriplett um „qf03+06“, durchgeführt am 14.08.09
nach der vierten Positionskorrektur um insgesamt weitere −320 µm.
89
B. Abbildungen
Abbildung B.1.: links: Frontansicht eines vollständig ausgestatteten Quadrupols mit
unterer Sextupolhälfte auf Girder. Auf dem Quadrupol aufgesetzt ist die Halterung zur
Aufnahme einer Taylor-Hobson-Kugeln für die geodätische Vermessung. rechts oben: Seitenansicht. rechts unten: Draufsicht der Quadrupollagerung [1].
91
Literaturverzeichnis
[1] Berges, U.: private Korrespondenz. DELTA, TU Dortmund, 2009
[2] Brinker, F.: Variable integrierte Sextupole für Speicherringe, Universität Dortmund, Diss., 1993
[3] Brinker, S. ; Heisterhagen, R. ; Wille, K.: DELTA beam position monitor.
In: Proc. IEEE Particle Accelerator Conferences, 1991, S. 1154 –1156 vol.2
[4] Elder, F. R. ; Langmuir, R. V. ; Pollock, H. C.: Radiation from Electrons
Accelerated in a Synchrotron. In: Phys. Rev. 74 (1948), Jul, Nr. 1, S. 52–56
[5] Finke, S.:
Fehlerrechnung bei der Auswertung physikalischer Messungen.
TU Dortmund. http://praktikum.physik.uni-dortmund.de/neu/a-praktikum/
anleitungen.html
[6] Giere, S. ; Kurrat, M. ; Schumann, U.: HV dielectric strength of shielding electrodes in vacuum circuit-breakers. In: 20th International Symposium on Discharges
and Electrical Insulation in Vacuum, 2002, S. 119–122
[7] Grewe, M.: SVD-basierte Orbitkorrektur am Speicherring Delta, Universität Dortmund, Diss., 2005
[8] Jankowiak, A.:
Kalibration der DELTA-Strahllagemonitore, Universität Dort-
mund, Diplomarbeit, 1994
[9] Jankowiak, A.:
Strahldiagnose und Closed-Orbit-Charakterisierung mit HF-
Strahllagemonitoren am Beispiel der Synchrotronstrahlungsquelle DELTA, Universität Dortmund, Diss., 1999
[10] Koch, A.S. ; Noll, T. ; Fölting, C. ; Schlüter, T.: Messgenauigkeit der induktiven Wegaufnehmer bei DELTA unter Berücksichtigung verschiedener Einflussfaktoren. Projektseminar, 2009
[11] Kopitetzki, O.: Vermessung und Modellierung der Optik des Speicherrings Delta,
Universität Dortmund, Diplomarbeit, 2005
93
Literaturverzeichnis
[12] Kopitetzki, O.: Iterativer Algorithmus zur strahlbasierten Vermessung und Korrektur von Magnetfehlaufstellungen am Speicherring Delta, TU Dortmund, Diss.,
2009
[13] Kopitetzki, O. ; Schirmer, D. ; Schmidt, G. ; Wille, K.: Beam Based Alignment of Quadrupole Tripletts by Use of MATLAB Based Modelling. In: Proc.
11th European Particle Accelerator Conference, 2008
[14] Kosicek, A.: Libera Electron User Manual, 2007. http://www.i-tech.si/
[15] MathWorks, The: MATLAB R2008a. http://www.mathworks.com
[16] Argonne National Laboratory: Experimental Physics and Industrial Control
System. http://www.aps.anl.gov/epics/index.php
[17] Bergoz Instrumentation: Bergoz BPM. http://www.bergoz.com
[18] Twk-Elektronik GmbH: Induktive Wegaufnehmer - Modellreihe IW 150. http:
//www.twk.de. Version: Juli 2007. – Technisches Datenblatt
[19] Okawa, M. ; Shioiri, T. ; Okubo, H. ; Yanabu, S.: Area effect on electric breakdown of copper and stainless steel electrodes in vacuum. In: Electrical Insulation,
IEEE Transactions on 23 (1988), Feb, Nr. 1, S. 77–81
[20] Press, W. H. ; Flannery, B. P. ; Teukolsky, S. A. ; Vetterling, W. T.:
Numerical Recipes in C. Cambridge University Press, 1992
[21] Schirmer, D.: Entwicklung von Strahloptiken für den Testspeicherring DELTA auf
Basis der Triplett-Struktur, Universität Dortmund, Diplomarbeit, 1989
[22] Schirmer, D.:
Entwurf und Auslegung eines supraleitenden asymmetrischen
Multipol-Wigglers zur Erzeugung intensiver Röntgenstrahlung mit variabler Polarisation am 1.5 GeV Elektronenspeicherring DELTA, Universität Dortmund, Diss.,
1994
[23] Schmidt, G.: private Korrespondenz. DELTA, TU Dortmund, 2009
[24] Schmidt, G. ; Berges, U. ; Friedl, J. ; Kasel, E. ; Wille, K. ; Zimoch, D.:
Position Sensors for Monitoring Accelerator Magnet Motion at Delta. In: Proc. 8th
European Particle Accelerator Conference, 2002, S. 2658–2660
[25] Schmidt, G. ; Kasel, E. ; D., Schirmer ; Zimoch, D. ; Wille, K.: Position
Monitoring of Accelerator Components as Magnets and Beam Position Monitors.
94
Literaturverzeichnis
In: Proc. 5th European Workshop on Beam Diagnostics and Instrumentation for
Particle Accelerators, 2001
[26] Straumann, T.: labCA - An EPICS Channel Access Interface for scilab and matlab.
http://www.slac.stanford.edu/comp/unix/package/epics/extensions/
labca/manual/manual.html. Version: May 2008
[27] Terebilo, A.: Accelerator Toolbox for MATLAB. http://ssrl.slac.stanford.
edu/at/. Version: 2001
[28] Towalski, P.: Implementierung einer schnellen lokalen Orbitkorrektur für den Speicherring Delta, TU Dortmund, Diplomarbeit, 2009
[29] Wiedemann, H.: Particle Accelerator Physics. Springer-Verlag Berlin Heidelberg,
2007
[30] Wille, K.:
Physik der Teilchenbeschleuniger und Synchrotronstrahlungsquellen.
B.G. Teubner Stuttgart, 1992
95
Danksagung
Ich danke Herrn Prof. Dr. Thomas Weis und Herrn Dr. Gerald Schmidt für die Vergabe
des Themas der vorliegenden Diplomarbeit und für die gute Betreuung bei der Bearbeitung. Herrn Prof. Dr. Carsten Westphal danke ich dafür, dass er die Bewertung dieser
Arbeit als Zweitgutachter übernommen hat.
Des Weiteren möchte ich mich bei Dr. Holger Huck und Dr. Detlev Schirmer für
die besonders kritische Korrektur dieser Arbeit bedanken, zu der in Teilen auch Dr.
Peter Hartmann beigetragen hat. Meinen Kollegen Bernard Riemann und Gerrit Schünemann danke ich für die vielen wissenschaftlichen und nichtwissenschaftlichen Diskussionen. Patryk Towalski danke ich insbesondere für die unermüdliche Unterstützung bei
„Software-Problemen“. Allen Mitarbeitern von DELTA danke ich auch für die stete Bereitschaft Fragestellungen zu diskutieren und die Unterstützung bei der Anfertigung dieser
Arbeit.
Abschließend möchte ich mich bei meiner Freundin Jessica bedanken, die mich während
der gesamten Arbeit unterstützt hat. Ganz besonders bedanke ich mich bei meinen Eltern,
die mir durch ihre Unterstützung das Physik-Studium und somit auch das Schreiben
dieser Arbeit überhaupt erst ermöglicht haben.
97