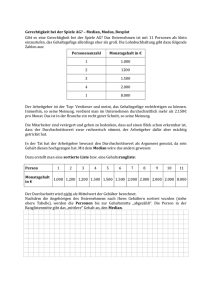
Deskriptive Statistik 1. Verteilungsformen symmetrisch

Deskriptive Statistik
1. Verteilungsformen
•
symmetrisch/asymmetrisch
•
unimodal(eingipflig) / bimodal (zweigipflig
•
schmalgipflig / breitgipflig
•
linkssteil / rechtssteil
•
U-förmig / abfallend
Statistische Kennwerte - Wieso braucht man diese
überhaupt?
Sie geben eine summarische Auskunft über die Verteilung. Alle Meßwerte sind zusammenfassend in einem
Kennwert repräsentiert.
Zwei Arten von deskriptiven Maßen:
1. Maße der zentralen Tendenz
2. Streuungsmaße (Dispersionsmaße)
1. Maße der zentralen Tendenz
Beispiel: Variable Anzahl der Geschwister aus Jugend '92
V189
ANZAHL GESCHWISTER
Value Label
TNZ
1 Geschwister
6 Geschwister
KA
Mean
Sum
1,295
5177,000
Value
Frequency
Percent
Valid
Percent
0
1
2
3
4
5
6
9
861
1824
854
296
89
49
26
6
------4005
1,000
21,5
45,5
21,3
7,4
2,2
1,2
,6
,1
------100,0
Mode
21,5
45,6
21,4
7,4
2,2
1,2
,7
Missing
------100,0
1,000
Total
Median
Modalwert oder Modus:
================ Deskriptive Statistik Seite 1 ======================
Cum
Percent
21,5
67,1
88,5
95,9
98,1
99,3
100,0
derjenige Wert einer Verteilung, der am häufigsten auftritt.
Wenn die Meßwerte in Kategorien zusammengefaßt
werden, gilt die Kategorienmitte der am häufigsten besetzten Kategorie als Modalwert. Die Angabe eines Modalwertes ist nur bei solchen Verteilungen üblich, die tatsächlich
ein Maximum besitzen (rechts und links vom Maximum
flacht der Verlauf ab).
Median
Der Wert einer mindestens ordinalskalierten Variable, der
die Häufigkeitsverteilung in zwei gleiche Hälften teilt.
Bei einer ungeraden Anzahl N der Daten ist der Median
der (N+1)/2te Wert.
Beispiel: N=7, d.h. 7 Werte: 4, 7, 1, 3, 9, 2, 11
Median ⇒ (7+1)/2 = 4. Wert
geordnete Werte 1, 2, 3, 4, 7, 9, 11
Bei einer geraden Anzahl N der Daten liegt der Median
zwischen dem N/2ten und dem (N+2)/2ten Wert.
Beispiel: N=8, d. h. 8 Werte: 4, 5, 7, 1, 3, 9, 2, 11
Median ⇒
zwischen N/2 =8/2= 4. Wert
und (N+2)/2= (8+2)/2= 10/2 = 5. Wert
geordnete Werte 1, 2, 3, 4, 5, 7, 9, 11
Der Median ist unempfindlich gegenüber Ausreißern.
Arithmetisches Mittel
Das gebräuchlichste Maß zur Kennzeichnung der zentralen
Tendenz.
================ Deskriptive Statistik Seite 2 ======================
Formel zur Berechnung - Summe aller Werte dividiert durch
die Anzahl der Werte:
_
n
Σ Xi
i=1
AM= x = 
n
Die Summe aller Abweichungen vom Mittelwert ergibt Null.
_
n
Σi=1 (Xi - X) = 0
Beispielberechnung
Mittelwert bei gruppierten Daten
_
m
Σ fk xk
AM= x = 
i=1
m
Σ fk
i=1
fk = Häufigkeit in der Kategorie k
xk = Kategorienmitte der Kategorie k
m = Anzahl der Kategorien
================ Deskriptive Statistik Seite 3 ======================
2.Streuungsmaße (Dispersionsmaße)
1. Variationsbreite, Variationsweite, Spannweite (range)
Variationsbreite = Maximum - Minimum
Nachteil dieses Maßes: es hängt nur von den Extremwerten ab
2. Perzentile (Prozentwerte der Verteilung)
Perzentile (1 bis 100) schneiden einen entsprechenden
Teil der Verteilungsfläche ab: das 5. Perzentil schneidet
die unteren 5%, das 95. Perzentil die oberen 5% ab.
Quartile teilen die Verteilung in vier gleich große Gruppen
(25., 50. und 75. Perzentil).
3. Die durchschnittliche Abweichung, AD-Streuung
)
Σ fk (Xk-X
m
i=1
AD=
n
Vorteil: Alle Werte werden berücksichtigt.
4. Varianz und Standardabweichung
Die Summe aller quadrierten Abweichungen aller Meßwerte vom arithmetischen Mittel, dividiert durch die Anzahl
aller Meßwerte.
================ Deskriptive Statistik Seite 4 ======================
Der Ausdruck im Zähler ⇒ Summe der Abweichungsquadrate, Quadratsumme (QS), sum of squares
In der Inferenzstatistik, wo die Stichprobenvarianz eine
Schätzung der Populationsvarianz ist, wird die Varianz so
berechnet:
VAR= S2 = = 
n -1
Die Standardabweichung
================ Deskriptive Statistik Seite 5 ======================
Die Streuungsbereiche der Normalverteilung:
Im Bereich x + s ⇒ ca. 2/3 aller Fälle = 68%
Im Bereich x + s ⇒ ca. 95% aller Fälle
================ Deskriptive Statistik Seite 6 ======================
Z-Transformation
Sinn und Zweck: Zwei Werte unterschiedlicher Skalen
dadurch vergleichbar machen, daß sie in Relation zum
Mittelwert und zur Standardabweichung gesetzt werden.
Standardisierung durch z-Transformation. Eine ztransformierte Verteilung hat einen Mittelwert von 0 und eine
Standardabweichung von 1.
Ein z-Wert (z-score) wird so berechnet:
_
(Xi - X)
zi = 
s
Schiefe und Exzeß
Schiefe ⇒ Maß für den Grad der Abweichung einer Verteilung von der Symmetrie
Schiefe= (Mittelwert - Modus) / Standardabweichung
Sch = 0 ⇒ symmetrische Verteilung
Sch < 0 ⇒ rechtssteile Verteilung
Sch > 0 ⇒ linkssteile Verteilung
Exzeß ⇒ Maß für den Grad der Häufung der Meßwerte um
einen Zentralpunkt, d.h. breitgipflig versus schmalgipflig.
================ Deskriptive Statistik Seite 7 ======================
Der Exzeß einer Normalverteilung beträgt 0,263, je größer
der Wert für den Exzeß, desto breitgipfliger ist der Verlauf
der Verteilung.
================ Deskriptive Statistik Seite 8 ======================