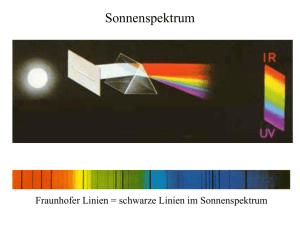
Optische Absorption
Werbung

Vorlesung “Charakterisierung von Halbleitermaterialien II” 4. Optische Spektroskopie Materials for Electronics and Energy Technology Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Begriffsbestimmung 4. Optische Spektroskopie Spektroskopie: Wellenlängenabhängige Messungen (Spektren) der (resonanten) Absorption und Emission von Photonen – Absorption Wellenlänge - - - - - Energie - - - - - - Wellenzahl - - - - - - Frequenz 7 1240 10 3×105 l [nm] E [eV] = –––––– n [cm–1] = ––––– f [THz] = ––––– l [nm] l [nm] l [nm] – Grundlagen und Aufbau – bandkantennahe Absorption – Störstellen- und Ladungsträgerabsorption – Absorption dünner Schichten – Reflexionsmessungen l > 1 mm Radiowellen (GHz/MHz-Bereich) 1 mm > l > 800 nm Infrarot IR (10–12000 cm–1 ) 800 nm > l > 400 nm sichtbares Licht 400 nm > l > 10 nm Ultraviolett UV 10 nm > l > 0,001 nm Röntgenstrahlen (keV-Bereich) – Lumineszenz – Raman-Spektroskopie – FT-IR-Spektroskopie (c) 2011 PD Dr. M. Bickermann, I-MEET, Uni Erlangen 4. Optische Spektroskopie 4. Optische Spektroskopie Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Energieniveaus (und ggf. Konzentrationen) bestimmen von 10 meV 100 μm 100 meV 10 μm IR – tiefen Störstellen 1 μm 1 eV VIS – Bandlücke – höheren Bändern – inneren Elektronen Þ chemische Analyse 10 eV 100 nm UV 10 nm 100 eV E l 1 nm Charakt Hableiter-Mat Matthias Bickermann Wellenlängenselektion: Monochromatoren Ziel der optischen Spektroskopie – Phononen, Exzitonen – flachen Störstellen Grundlagen und Aufbau Es werden immer Übergänge zwischen Zuständen betrachtet! Meist wird in Referenz zur Leitungsbandkante gemessen (Rekomb. von Elektronen), der Bereich der Bandlücke ist also besonders interessant! A: Eintreffendes Licht B: Eingangsspalt C: Erster Linsenspiegel D: drehbares Beugungsgitter (geritzt oder holographisch) E: Zweiter Linsenspiegel F: Ausgangsspalt G: Austretendes Licht – Höhere Linienzahl Þ größere Aufspaltung (geringere Intensität) – Nullte Ordnung: Gitter wird zum Spiegel bei l = 0 – Höhere Ordnungen: Auch l/n-Anteile (Ausfiltern z.B. durch Filterrad) 4. Optische Spektroskopie 4. Optische Spektroskopie Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Absorptionsmessplatz: Spektrophotometer Wechselwirkung von Licht (Photonen) mit Materie (Lampe – Monochromator – Probe – Detektor) Senkrechter Durchgang durch eine planparallele Platte: An jeder Grenzschicht wird ein Teil der elektromagnetischen Welle reflektiert und transmittiert. Spiegelchopper Strahlsammler Monochromator Lichtquelle ( ( Detektor 200 Filterrad Spiegel Probe Spiegel 400 600 800 nm Spektrum Deuteriumlampe Es gilt (für k® 0): T1 ×T2 = 1–R Luft (n = 1) Der Brechungsindex n ist eigentlich komplex (n~ = n +ik), man rechnet hier aber nur mit dem Realteil und berücksichtigt die Absorption über das Lambert-Beer’sche Gesetz: Referenzstrahl: Messung der Intensität ohne Probe Nutzbares Spektrum max. 170–4000 nm – UV: Deuteriumlampe + Photomultiplier/Si-Diode – VIS: Wolframlampe + Photomultiplier/Si-Diode – IR: Wolframlampe + InGaAs-Diode (bis 1600 nm) oder PbS-Schirm (bis 3500 nm) )2 + k² )2 + k² I – = e –ad I0 350 Þ 1 ln (I/I ) a=–– 0 Luft (n = 1) d 1000 1500 2000 2500 nm Spektrum Wolframlampe 4. Optische Spektroskopie I/I0 wird mit dem Spektrophotometer gemessen, d ist die Dicke der Probe. 4. Optische Spektroskopie Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Grundlagen und Aufbau Charakt Hableiter-Mat Matthias Bickermann Messgrenzen bei der Absorption Reflektionskorrektur Lambert-Beer’sche Gesetz: R wird nicht berücksichtigt Þ berechnetes a zu hoch Einfachreflexion (grüne Pfeile) berücksichtigt: [Achtung: n(l) muss hierfür bekannt sein!] I – = T1 T2 e–ad I0 Þ Annahme: senkrechter Lichteinfall! a = – 1– ln (I/I0 ) + 1 – ln (T1T2) d d Þ berechnetes a zu niedrig Luft (n = 1) Mehrfachreflexion über geometrische Reihe: (quadratische Gleichung in a) Luft (n = 1) Fabry-Perot-Oszillationen bei dünnen Schichten Einfluss der Oberflächenrauigkeit Maximale/minimale Absorptionskoeffizienten (SiC, Politur mit untersch. Körnung) 4. Optische Spektroskopie 4. Optische Spektroskopie Absorption in Halbleitern und Isolatoren Charakt Hableiter-Mat Matthias Bickermann Optische Absorptionsspektren zeigen energetische Übergänge in der Bandlücke. Näherungsweise gilt: a×E = B (E – Eg) n Þ Bestimmung der Bandlücke Eg Tauc, Grigorovici and Vancu, Phys. Stat. Sol. 15, 627 (1966) Bei amorphen und indirekten Halbleitern gilt n = 2 (Wurzelauftragung). Absorption freier Ladungsträger Photoionisation (flacher Störstellen) Störstellenumladung / Intraschalenübergänge Die Auftragung a×E 1/n über E nennt man Tauc-Plot. resonante Anregung (z.B. mit höherem Leitungsband) Absorpt. tiefer Störstellen exzitonische Absorption 0 fundamentale Absorption conduction band e+h Charakt Hableiter-Mat Matthias Bickermann 1. Absorption an/in der Bandkante Energy Eg Absorption in Halbleitern und Isolatoren Bei direkten Halbleitern setzt man n = 1/2 an (Quadratauftragung). Der Anstieg von a(E) an der Bandkante ist also bei direkten Halbleitern wesentlich steiler. Weit hinter der Bandkante haben Halbleiter typischerweise a » 106 cm –1 valence band 4. Optische Spektroskopie Absorption in Halbleitern und Isolatoren 4. Optische Spektroskopie Charakt Hableiter-Mat Matthias Bickermann Absorption in Halbleitern und Isolatoren 1. Absorption indirekter Halbleiter an/in der Bandkante 2. Bandkantennahe Absorption Ein Phonon muss den Wellenvektor ausgleichen Þ “Bandkante” bei Eg – –hW Þ (fast) keine Absorption an Eg, dafür Þ geringere Wahrscheinlichkeit an höheren direkten Bandübergängen Þ geringere Absorption – freie/gebundene Exzitonen (Elektron-Loch-Paare) Absorptionsbande, meist nur bei tiefen Temperaturen sichtbar (siehe Þ Lumineszenz) Charakt Hableiter-Mat Matthias Bickermann GaAs, 21 K – Amorphe Halbleiter: “Urbach-Tail” Unterhalb der Bandlücke gilt a ~ exp(E/Eu) (exponentielles Abklingen) mit der “Urbach-Energie” Eu (Dangling bonds, Gitterstörungen) Þ Bestimmung der Exzitonen-Bindungsenergie Eex 4. Optische Spektroskopie 4. Optische Spektroskopie Absorption in Halbleitern und Isolatoren Charakt Hableiter-Mat Matthias Bickermann Þ Bestimmung der Lage der Störstelle, z.B. ED und (nach Eichung) ihrer Konzentration 3. Störstellenabsorption Absorption in Halbleitern und Isolatoren Charakt Hableiter-Mat Matthias Bickermann 4. Photoionisation und Absorption freier Ladungsträger Beide zeigen ein a ~ l²-Verhalten weit weg von der Bandkante (d.h. im Infrarotbereich). Beide sind in etwa proportional zur Störstellen- bzw. Ladungsträgerdichte. Beide hängen stark von der Temperatur ab (Besetzungswahrscheinlichkeit, Fermistatistik). Absorption tiefer Störstellen in AlN. Die Banden sind verbreitert, wenn der Anfangs- oder Endzustand selbst ein Band ist. Absorption von 3d-Intraschalenübergängen von V 4+ in SiC. Diese Übergänge sind schmal, verbreitern sich aber bei hohen Temperaturen. freie Ladungsträger 4. Optische Spektroskopie Photoionisation flacher Störstellen 4. Optische Spektroskopie Absorption in Halbleitern und Isolatoren Charakt Hableiter-Mat Matthias Bickermann Charakt Hableiter-Mat Matthias Bickermann Dünne Schichten (d » l): Fabry-Pérot-Oszillationen 5. Absorption flacher Störstellen - - Absorption dünner Schichten Wie bestimmt man a(l)? l » 8,5 μm l » 35 μm in Si in Si Absorptionsbanden (energetische Übergänge oder local vibrational modes) sind erst im mittleren/fernen IR sichtbar Þ Infrarot-Spektroskopie Peakhöhe proportional zur Nettodotierkonzentration ND –NA Absorptionsspektren von amorphen AlN-SiC-Schichten von ca. 300 nm Dicke und unterschiedlicher Zusammensetzung 4. Optische Spektroskopie Wie bestimmt man a(l)? – geometrische Mittelung der Einhüllenden TM und Tm – schneidet Wendepunkte der oszillierenden Kurve Auswertung der Oszillationen? – Dicke d (aus Oszillations-Frequenz) – Brechungsindex n (aus Oszillations-Amplitude) – Absorption des Substrates (bei halbtransparenter Schicht) – Oszillationen verschwinden an der Bandlücke Þ Eg Achtung: Interpretation wird schwierig bei Mehrschichtstrukturen, rauen Oberflächen, nicht senkrechtem Lichteinfall oder inhomogenen Materialeigenschaften. 4. Optische Spektroskopie Bestimmung des absorbierenden Anteils über Reflexion bei stark absorbierenden Schichten (oder Schichten auf stark absorbierenden Substraten) Ulbricht-Kugel Strahlsammler Probe Probe Monochromator Lichtquelle Probe Filterrad 90°-Anordnung 45°-Anordnung diffuse Reflexion Referenzmessung: Spiegel (Ulbrichtkugel: Weißstandard) an Stelle der Probe Auswertemöglichkeiten: – Abweichung des Brechungsindex bei elektronischen Übergängen (Bandkante) – Rückrechnen von der Vielfachreflexion auf den transmittierten Anteil – Bestimmung von n(l) und a(l) aus Transmissions- und Reflexionsmessung 4. Optische Spektroskopie Reflexionsmessungen Charakt Hableiter-Mat Matthias Bickermann UV-Reflexionsmessungen einer 1,1 μm dicken AlN-Schicht auf (intransparentem) SiC-Substrat nahe der Bandkante. Der komplexe Brechungsindex (bzw. die dielektrische Funktion) ändert sich an der Stelle der exzitonischen Absorption. 90°-Geometrie XB,C 45°-Geometrie Charakt Hableiter-Mat Matthias Bickermann Detektor Dünne Schichten (d » l): Fabry-Pérot-Oszillationen Reflexionsmessungen Detektor Absorption dünner Schichten Charakt Hableiter-Mat Matthias Bickermann Detektor 4. Optische Spektroskopie Außerdem verschwinden die Fabry-Pérot-Oszillationen an der Bandkante (hier: XB,C ). Das A-Valenzband kann nur für E || c als Endzustand des Lochs fungieren. Þ Absorption und Reflexion können polarisationsabhängig sein!!! Literatur Charakt Hableiter-Mat Matthias Bickermann Literatur zur optischen Spektroskopie und Absorption – W. Schmidt, Optische Spektroskopie, Wiley-VCH, Weinheim 2000. – M. Fox, Optical Properties of Solids, Oxford University Press, Oxford 2003. – H. Kuzmany, Festkörperspektroskopie, Springer Verlag, Berlin 1989. – J. Garcia Sole, L.E. Bausa, D. Jaque, An Introduction to the Optical Spectroscopy of Inorganic Solids, Wiley, New York 1981. – B. Henderson, G. F. Imbusch, Optical Spectroscopy of Inorganic Solids, Clarendon Press, Oxford 1989. – R. Weingärtner, Bestimmung der Ladungsträgerkonzentration und Kompensation in Siliziumkarbid mittels optischer und elektrischer Methoden, Dissertation, Universität Erlangen-Nürnberg 2003 Optische Spektroskopie an dünnen Schichten – R. Swanepoel, J. Phys. E: Sci. Instrum. 16 (1983) 1214. – J.C. Manifacier, J. Gasiot, J.P. Fillard, J. Phys. E: Sci. Instrum. 9 (1976) 1002. – O. S. Heavens, Optical Properties of Thin Solid Films, Dover Publications, Mineola (NY) USA 1991.