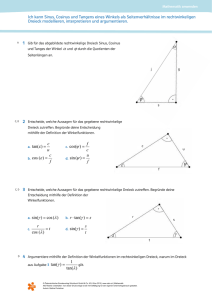
ψ λ γ = λ γ =
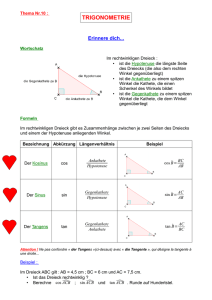
Werbung
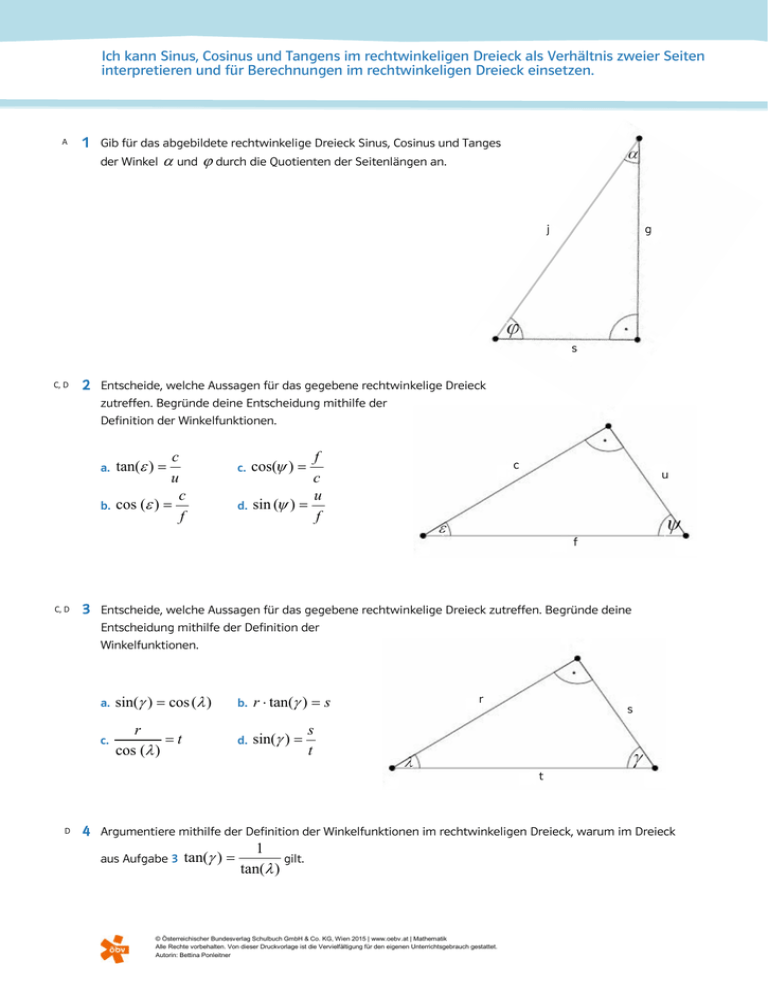
Ich kann Sinus, Cosinus und Tangens im rechtwinkeligen Dreieck als Verhältnis zweier Seiten interpretieren und für Berechnungen im rechtwinkeligen Dreieck einsetzen. A 1 Gib für das abgebildete rechtwinkelige Dreieck Sinus, Cosinus und Tanges der Winkel α und ϕ durch die Quotienten der Seitenlängen an. j g s C, D 2 Entscheide, welche Aussagen für das gegebene rechtwinkelige Dreieck zutreffen. Begründe deine Entscheidung mithilfe der Definition der Winkelfunktionen. a. b. c u c cos (ε ) = f tan(ε ) = c. d. f c u sin (ψ ) = f cos(ψ ) = c u f C, D 3 Entscheide, welche Aussagen für das gegebene rechtwinkelige Dreieck zutreffen. Begründe deine Entscheidung mithilfe der Definition der Winkelfunktionen. a. sin(γ ) = cos (λ ) b. r ⋅ tan(γ ) = s c. r =t cos (λ ) d. sin(γ ) = r s s t t D 4 Argumentiere mithilfe der Definition der Winkelfunktionen im rechtwinkeligen Dreieck, warum im Dreieck 1 aus Aufgabe 3 tan(γ ) = gilt. tan(λ ) © Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015 | www.oebv.at | Mathematik Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet. Autorin: Bettina Ponleitner Ich kann Sinus, Cosinus und Tangens im rechtwinkeligen Dreieck als Verhältnis zweier Seiten interpretieren und für Berechnungen im rechtwinkeligen Dreieck einsetzen. A, B, C 5 Vor dem Eingang eines Veranstaltungszentrums soll neben den schon vorhandenen Stufen eine geradlinige Auffahrtsrampe gebaut werden. Der zu überwindende Höhenunterschied beträgt 65cm. Die Steigung der Rampe ist mit maximal 3° vorgegeben. Aufgrund der baulichen Gegebenheiten darf der horizontale Abstand von Rampenanfang bis Rampenende höchstens 12,5m betragen. a. Berechne, ob es unter diesen Bedingungen möglich ist, eine geradlinige Rampe zu bauen. b. Berechne die Länge der Rampe. B 6 Von einem rechtwinkeligen Dreieck kennt man die Hypotenuse c = 24 cm und den Winkel α = 50° . Berechne die fehlenden Seitenlängen und Winkel, sowie den Flächeninhalt des Dreiecks. A, B 7 Georg und Sabine wollen im Garten ein Gehege für ihre Meerschweinchen bauen. Der Grundriss des Geheges soll 1,2m ein rechtwinkeliges Dreieck sein (siehe Skizze). Die beiden Katheten des Dreiecks liegen an der Gartenmauer, entlang der Hypotenuse wollen Georg und Sabine einen Zaun ε aufstellen. Eine Kathete soll 1,2 m lang sein. Es stehen 1,8m Zaun zur Verfügung. 1,8 m a. Berechne den Winkel ε , der zwischen der gegebenen Kathete und der Hypotenuse liegt. b. Berechne die Länge der anderen Kathete. c. Berechne den Flächeninhalt des Geheges. B 8 Von einem rechtwinkeligen Dreieck (siehe Skizze) kennt man eine Seite und einen Winkel. Berechne die übrigen Bestimmungsstücke. α a. 14 cm 306 cm 66° c a 27 cm 48° c. A, B b 35° b. d. β b a α 524 cm c 214 cm 9 Ein Radfahrer fährt eine Gebirgsstraße bergab. Der Kilometerzähler zeigt eine zurückgelegte Strecke von 1528 m an. Laut Höhenmesser hat der Radfahrer dabei einen Höhenunterschied von 140 m überwunden. Berechne den Steigungswinkel der Straße. © Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015 | www.oebv.at | Mathematik Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet. Autorin: Bettina Ponleitner β Mathematik anwenden Lösungen zu: Ich kann Sinus, Cosinus und Tangens im rechtwinkeligen Dreieck als Verhältnis zweier Seiten interpretieren und für Berechnungen im rechtwinkeligen Dreieck einsetzen. g j s cos (j ) = j s j g sin(j ) = j 1 sin (α ) = cos (α ) = s g g tan(ϕ ) = s tan (a ) = 2 a. falsch: An- und Gegenkathete sind vertauscht; es gilt: tan (ε ) = u c b. richtig c. falsch: Cosinus ist Ankathete durch Hypotenuse, daher gilt: cos(ψ ) = u f d. falsch: Hier wurde die Ankathete anstelle der Gegenkathete verwendet; es gilt: sin(ψ ) c f G r A r = , cos(λ ) = = H t H t 3 a. richtig, da sin(γ ) = 4 = b. falsch, da tan(γ ) = G r = ⇒ s ⋅ tan (γ ) = r A s c. richtig, da cos(λ ) = r r ⇒ =t t cos(λ ) d. falsch, da sin (γ ) = G r = H t 1 1 r = s = = tan(γ ) tan(λ ) r s 5 a. Ja, die Rampe kann gebaut werden, da der horizontale Abstand unter diesen Bedingungen etwa 12,4 m beträgt. b. Länge der Rampe: 12,42m 6 a = 18,4 cm; b = 15,4 cm; β = 40° ; A = 142cm 2 7 a. ε = 48,2° b. Kathetenlänge: 1,3 m 2 c. A ≈ 0,8m © Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015 | www.oebv.at | Mathematik Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet. Autorin: Bettina Ponleitner Mathematik anwenden Lösungen zu: Ich kann Sinus, Cosinus und Tangens im rechtwinkeligen Dreieck als Verhältnis zweier Seiten interpretieren und für Berechnungen im rechtwinkeligen Dreieck einsetzen. 8 Von einem rechtwinkeligen Dreieck (siehe Skizze) kennt man eine Seite und einen Winkel. Berechne die übrigen Bestimmungsstücke. a. b. c. d. α β a b c 35° 42° 36° 66° 55° 48° 54° 24° 15 cm 13 cm 306 cm 481 cm 22 cm 14 cm 425 cm 214 cm 27 cm 19 cm 524 cm 526 cm b α 9 Steigungswinkel: 5,26° © Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015 | www.oebv.at | Mathematik Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet. Autorin: Bettina Ponleitner a c β