ψ γ ϕ

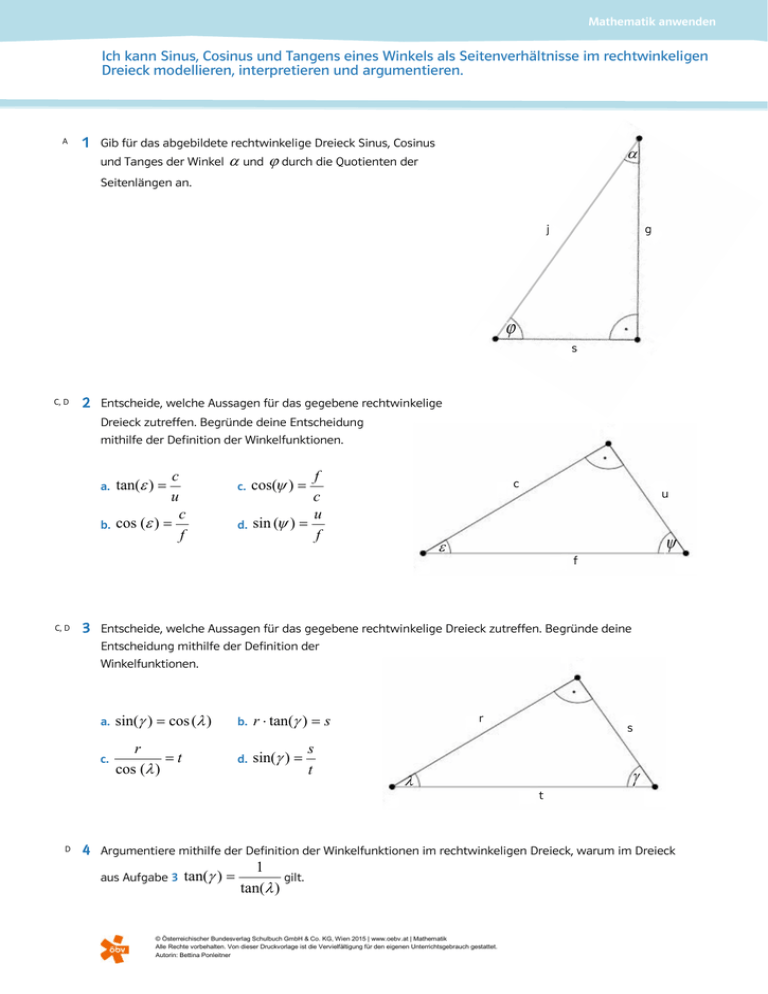
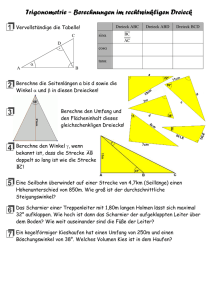
Mathematik anwenden
Ich kann Sinus, Cosinus und Tangens eines Winkels als Seitenverhältnisse im rechtwinkeligen
Dreieck modellieren, interpretieren und argumentieren.
A
1 Gib für das abgebildete rechtwinkelige Dreieck Sinus, Cosinus
und Tanges der Winkel
α
α und ϕ durch die Quotienten der
Seitenlängen an.
j
g
ϕ
s
C, D
2 Entscheide, welche Aussagen für das gegebene rechtwinkelige
Dreieck zutreffen. Begründe deine Entscheidung
mithilfe der Definition der Winkelfunktionen.
a.
b.
C, D
c
u
c
cos (ε ) =
f
tan(ε ) =
c.
d.
f
c
u
sin (ψ ) =
f
cos(ψ ) =
c
u
ψ
ε
f
3 Entscheide, welche Aussagen für das gegebene rechtwinkelige Dreieck zutreffen. Begründe deine
Entscheidung mithilfe der Definition der
Winkelfunktionen.
D
a.
sin(γ ) = cos (λ )
b.
r ⋅ tan(γ ) = s
c.
r
=t
cos (λ )
d.
sin(γ ) =
s
t
r
λ
s
γ
t
4 Argumentiere mithilfe der Definition der Winkelfunktionen im rechtwinkeligen Dreieck, warum im Dreieck
1
aus Aufgabe 3 tan(γ ) =
gilt.
tan(λ )
© Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015 | www.oebv.at | Mathematik
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet.
Autorin: Bettina Ponleitner
Mathematik anwenden
Lösungen zu:
Ich kann Sinus, Cosinus und Tangens eines Winkels als Seitenverhältnisse im rechtwinkeligen
Dreieck modellieren, interpretieren und argumentieren.
1 sin (α ) =
s
j
cos (α ) =
g
j
tan (a ) =
s
g
sin(j ) =
g
j
cos (j ) =
s
j
tan(ϕ ) =
g
s
2 a. falsch: An- und Gegenkathete sind vertauscht; es gilt: tan (ε ) =
u
c
b. richtig
c. falsch: Cosinus ist Ankathete durch Hypotenuse, daher gilt:
cos(ψ ) =
u
f
d. falsch: Hier wurde die Ankathete anstelle der Gegenkathete verwendet; es gilt: sin(ψ )
3 a. richtig, da sin(γ ) =
4
G r
A r
= , cos(λ ) =
=
H t
H t
b. falsch, da
tan(γ ) =
G r
= ⇒ s ⋅ tan (γ ) = r
A s
c. richtig, da
cos(λ ) =
r
r
⇒
=t
t
cos(λ )
d. falsch, da
sin (γ ) =
G r
=
H t
1
1 r
= s = = tan(γ )
tan(λ ) r s
© Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2014 | www.oebv.at | Mathematik
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet.
Autorin: Bettina Ponleitner
=
c
f