ueb7_0105

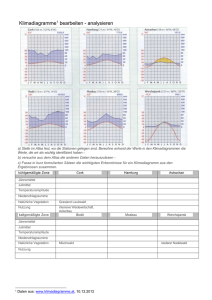
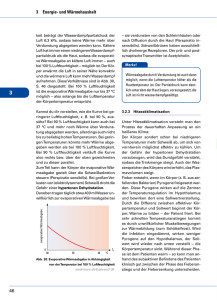
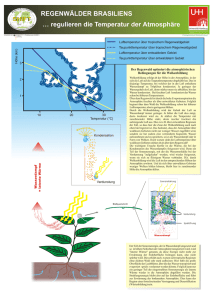
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
Evapotranspiration eines Fichtenaltbestandes
1. Einleitung
In dieser Übung geht es um die Evapotranspiration eines Fichtenbestandes im Solling. Mit der
Verdunstung von Wasser geht ein Energiefluss in Form von latenter Wärme einher, dem
System wird durch den Energieaufwand für den Phasenübergang Wärme entzogen und so in
der Atmosphäre gespeichert. Diese latente Energie wird bei Kondensationsprozessen wieder
frei und führt zur Erwärmung von Luft und Boden. Der Gewinn an Kondensationsenergie z.
B. durch Ausregnen kann 30% der Sonnenenergie ausmachen (HÄCKEL). Auf diese Art
können große Energiemengen beispielsweise den heißen und feuchten Tropen entzogen
werden und an anderen, kühleren Orten durch Kondensationsprozesse zur Erwärmung führen.
Dadurch ergibt sich die bedeutende klimatisierende Wirkung des Wassers.
Wieviel Wasser pro Fläche und Zeit verdunstet wird, hängt im wesentlichen von der relativen
Feuchte und der Temperatur ab. Je wärmer die Luft ist, desto mehr Wasser kann sie in Form
von Wasserdampf speichern und wird sie so der Erdoberfläche entziehen. Auf diese Weise
stellt sich nach einiger Zeit bei unbewegter Luft der Sättigungsdampfdruck ein und es kommt
bei konstanter Temperatur zu keinen weiteren Verdunstungsvorgängen. Werden jedoch
ständig neue ungesättigte Luftpakete durch den Wind an die verdunstende Oberfläche
herangeführt, so wird mehr Wasser verdunstet. Die Verdunstungsmenge hängt also auch von
einer Art Leitfähigkeit der Atmosphäre ab, daher kann die Verdunstungsmenge und der damit
einhergehende Energiefluss über Transportwiderstände berechnet werden.
Der aerodynamischen Transportwiderstand und der Grenzschichtwiderstand wurden für den
Fichtenstand bereits in der vorherigen Übung berechnet. Diese Widerstände hängen im
wesentlich von der Windgeschwindigkeit ab und gelten für alle möglichen Massenflüsse von
in der Atmosphäre befindlichen Stoffen. Bei dem Transport von Wasser und latenter Wärme
vom Waldbestand in die Atmosphäre durch Verdunstungsvorgänge kommt zu dieser Reihe
von Widerständen noch ein weiterer Widerstand hinzu, da die Vegetation einen beträchtlichen
Anteil zur verdunsteten Wassermenge beisteuert, der durch die Atmungs- und
Photosynthesevorgänge in den Blättern gesteuert wird. Es handelt sich hierbei um den
Stomatawiderstand, der von Faktoren wie der Globalstrahlung und der Temperatur abhängt.
Ihn wollen wir in dieser Übung als Weiterführung von Übung 6 zunächst berechnen. So kann
dann mithilfe der vollständigen Reihe von Widerständen die verdunstete Wassermenge und
-1-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
die darin gebundene Energie für den Monat Oktober des Jahres 1997 berechnet werden. Des
Weiteren wird der Unterschied zwischen aktueller und potentieller Verdunstung untersucht
und sich mit der Form der Energieabgabe als fühlbarer und latenter Wärmestrom beschäftigt.
2.Theorie
2.1 Stomatawiderstandsmodell nach Wesley
Die Transpiration von Pflanzen wird durch die Spaltöffnungen gesteuert. Bei geschlossener
Spaltöffnung ist der Widerstand hoch, bei geöffneter ist er klein. Die Öffnung der Stomata
hängt von der Blatttemperatur und der Sonneneinstrahlung ab. Wesley et. al. (1989) fanden
folgende Parametrisierung für die Reaktion der Pflanzen auf die mikrometeorologischen
Umgebungsbedingungen:
(Gl. 1)
Dabei bedeutet Q die Intensität der Globalstrahlung in W/m2 und T die Temperatur in °C.
Bei einer Strahlungsflussdichte für die Globalstrahlung von weniger als 50 W/m2 (z.B.
nachts) wird angenommen, dass die Stomata vollständig geschlossen sind und dennoch
„unfreiwillig“ über die Cuticula geatmet und transpiriert wird. Der Widerstand wird daher
auch nicht unendlich hoch sondern soll einen Maximalwert von rs = 2000 s/m annehmen.
2.2 Verdunstung und latenter Wärmestrom
Für die Verdunstung von einem kg Wasser wird eine Energie von etwa 2,5 MJ verbraucht.
Diese als latente Wärme gespeicherte Energiemenge (Verdampfungswärme) entstammt der
Einstrahlung und dem Bodenwärmestrom. Die Einstrahlung erhöht die zur Verfügung
stehende Energie und wird erniedrigt durch den Bodenwärmestrom. Bei ungehinderter
Nachlieferung von Wasser wird diese Energie vollständig zur Verdunstung genutzt. So kann
über die Energiebilanz und das Sättigungsdampfdruckdefizit in Abhängigkeit von der
Temperatur mithilfe der Transportwiderstände diese Energiemenge berechnet werden. Auf
Penman geht folgende Gleichung zurück:
-2-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
(Gl.2)
Der rechte Term ist der latente Wärmestrom, Rn die Strahlungsbilanz und G der
Bodenwärmestrom. Für die Bedeutung der anderen Konstanten siehe Erläuterungen im Skript.
Durch Division des Ergebnisses durch die Verdampfungswärme lässt sich mithilfe dieser
Gleichung die Wassermenge berechnen, die von einer freien Wasseroberfläche mit
ungehinderter Wassernachlieferung verdunstet wird.
Jedoch ist die Evapotranaspiration von Vegetationsoberfläche nicht gleichbedeutend mit der
potentiellen Verdunstung, letztere wird durch die Regulierung der Schließzellen der Pflanzen
immer kleiner sein. Monteith erweiterte 1968 die Gleichung, in dem er die
Transportwiderstände integrierte und so ein „Big Leaf“ Modell schuf:
(Gl. 3)
Der Stomatawiderstand findet sich in der Gleichung ebenso wieder wie der aerodynamische
(ra) und der Grenzschichtwiderstand (rb). Auf diese Weise kann nun der Energiefluss bei
aktueller Verdunstung (rs > 0) sowie die potentiellen Verdunstung (rs = 0) berechnet werden.
Die Evapotranspiration kann, neben der Möglichkeit diese mit der Penman-MonteithGleichung zu berechnen, auch mit der Eddy-Covarianz-Methode bestimmt werden. Bei
diesem
Verfahren
wird
die
Turbulenz
über
Windgeschwindigkeitsmessungen
bestimmt.
Durch
der
Vegetation
Kombination
mit
Hilfe
von
dieser
Werte
mit
Temperatur- und Feuchtemessungen kann auf die Größe der Luftpakete geschlossen werden,
die mit der Vegetation ausgetauscht werden. Wasser- und CO2-Flüsse können auf
Bestandesebene erfasst werden, wenn man zusätzlich die chemischen Inhalte der Luft kennt.
Diese Methode kann allerdings nur bei bestimmten topographischen Bedingungen
angewendet werden. Störend wirken sich stabile Schichtung, heterogene Umgebung und
große Hangneigung aus (SCHULZE ET AL. 2002).
Die Eddy-Covarianz-Methode wurde genutzt um den fühlbaren Wärmestrom und die
Evapotranspiration zu bestimmen.
-3-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
2.3 Bowensverhältnis
Um zu ermitteln in welcher Form die dem Boden bzw. der Pflanze zugeführte Energie
verbraucht wird bedient man sich des Bowensverhältnisses:
β=
H
(Gl. 4)
λE
Dabei beschreibt H den fühlbaren Wärmestrom und λE die Verdunstungsenergie. Beide
Größen werden in W/m² angegeben. Erreicht dieses Verhältnis Werte >1 so bedeutet dies, das
mehr Energie in Form von fühlbarer Wärme abgegeben wird als zur Verdunstung benötigt
wird. Nimmt es Werte <1 an wird mehr Energie zur Verdunstung aufgewandt als in Form von
fühlbarer Wärme abgegeben wird. Ist der Wert 1 so sind beide Energieströme gleich groß.
Durch internationale Konventionen wurde festgelegt, dass ein nach oben gerichteter
Energiefluss von H und λE ein positives Vorzeichen erhält. Somit wird β negativ, wenn der
Boden kälter ist als die Atmosphäre. Negative Werte für β kommen zudem bei der
Taubildung und Regenfällen vor.
-4-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
3. Methoden: SAS-Code
3.1 Berechnung der Widerstände
Für den Monat September wurden mittels der vorhandenen Daten zunächst die Widerstände
berechnet:
%let Z0_1 = 2.6; %let D_1=22;/*aerodynamische Eigenschaften der Fichtenfläche F1 */
data f1EvapOct;
set f1evap;
if "1Oct1997:00:00:00"dt <= saszeit <= "1Nov1997:00:00:00"dt;
hour = hour(saszeit) +0.5;
/* empirisches Stomatawiderstandsmodell
Eingangsvariablen:
Globalstrahlung (G_So ) in W/m²
Lufttemperatur (TT_So) in °C
Ausgabe:
Stomatawiderstand (rs) in s/m
*/
if
G_so
>
50
and
TT_so
>0
then
rs
=
130
*(1+(200/(G_so+0.1))**2)
*
400/(TT_so*(40-TT_so));
else rs = 2000; /* nächtlicher Wert des Stomatawiderstands */
if rs > 2000 then rs = 2000;
/* Schubspannungsgeschwindigkeit berechen */
ustar=WG_39*0.41/log((39-&d_1)/&Z0_1); /* m/s
vgl. oben : aerodynamische
Parameter für Fichtenwald */
if USTAR > 0 then do;
ra = WG_39/(USTAR**2); /* s/m */
Rb = 2 /(USTAR*0.41)* (22.2E-6/24.9e-6)**(2/3); /* s/m */
end;
Dabei wird der stomatäre Widerstand (rs) mithilfe einer Wenn-Dann-Sonst-Funktion auf
einen Maximalwert von 2000 s/m nach oben hin begrenzt. Diesen Maximalwert soll erreicht
werden, wenn die Globalstrahlung einen Wert kleiner als 50 W/m2 annimmt. Bei höheren
Werten wird der stomatäre Transportwiderstand nach Wesley (s. Gl.1) berechnet.
Die anderen Widerstände werden wie in Übung 6 berechnet.
-5-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
3.2 Latente Wärmeströme
Mithilfe der oben berechneten Widerstände wurden dann die latenten Wärmeströme für die
aktuelle und die potentielle Verdunstung berechnet. Die Verdampfungswärme λw (lmbdw)
wurde hier inklusive ihrer geringen linearen Temperaturabhängigkeit berechnet.
cp = 1004; /* J/(K kg) spezifische Wärmekapazität der Luft bei konstantem
Druck */
rho= P_02 * 100/(287.01 * (TT_so + 273.15)); /* kg/m² Luftdichte in */
lmbdw=(2.5008-0.002372*(TT_so))*1e6;/* latente Verdampfungswaerme in [J/kg] */
Es= 610.78*exp(17.08085*(TT_so)/(234.175+TT_so)) ;/* Saettigungsdampfruck Pa*/
delta=ES*3999.9080/(234.175+TT_so)/(234.175+TT_So);
/*
Steigung
der
Sättignungsdampfdruckkurve über der Temperatur Pa/K*/
gamma=1004*(P_02*100)/(0.622*lmbdw);/* Psychrometerkonstante
lE_PM
Pa / K */
=(delta*(RN-G)+rho * CP*(VPD)/(ra+rb))/( delta+gamma*(1+rs/(ra+rb)) );
/* Verdunstungrate nach Penman Monteith W/m²*/
lE_PM_pot=(delta*(RN-G)+rho * CP*(VPD)/(ra+rb))/( delta+gamma*(1+0 /(ra+rb)) );
/* potenzielle Verdunstung nach Penman Monteith W/m²*/
3.3 Bowensverhältnis
Das Bowensverhälnis wurde auf drei verschiedene Weisen berechnet. Die Werte des latenten
Wämestroms wurden in allen Fällen mit der Eddy-Covarianz-Methode berechnet. Zum einen
wurde der Quotient aus fühlbarem Wärmestrom und aktueller Verdunstung nach PenmanMonteith gebildet (bowen_1). Zum anderen wurde das Verhältnis von H und potentieller
Evapotranspiration nach Penman-Monteith berechnet (bowen_2). Schließlich wurde die mit
der
Eddy-Covarianz-Methode
bestimmte
Evapotranspiration
durch
den
fühlbaren
Wärmestrom dividiert (bowen_3).
bowen_1 = SHF_tc/lE_Pm;
/*aktuelle Verdunstung und eddifluxmessungen */
bowen_2 = SHF_tc/lE_Pm_pot;
/* potentielle Verdunstung und eddiflux*/
bowen_3 = SHF_tc/LHF_tc;
/* latent und H aus eddiflux */
-6-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
3.4 Wassermenge
Die verdunstete Wassermenge wurde durch Division der unterschiedlich ermittelten latenten
Wärmeströme (W/m2) durch die Verdampfungsenthalpie λ berechnet, und dann auf die
Stunde hochgerechnet.
wasser1 = lE_PM/lmbdw*3600; /*verdunstete Wassermenge pro m2 und h*/
wasser2 = lE_PM_pot/lmbdw*3600;
wasser3 = LHF_tc/lmbdw*3600;
-7-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
4. Ergebnisse
4.1 Transportwiderstände
In Abbildung 1 sind die mittleren monatlichen Tagesgänge der Transportwiderstände für den
Monat September dargestellt. Im Vergleich zum stomatären Widerstand (rs) sind der
Grenzschichtwiderstand (rb)
und der aerodynamische Widerstand (ra) sehr klein. Der
Stomatawiderstand erreicht nachts einen Maximalwert von 2000 s/m, bei Tagesbeginn um 6
Uhr morgens fällt er sehr rasch ab und ist in der Zeit von ca. 10 bis 16 Uhr bei ca. 200-300
s/m. Ab 16 Uhr steigt der Widerstand steil an und hat gegen 18 Uhr den Maximalwert wieder
erreicht.
Abbildung 1: Der mittlere monatliche Tagesgang der Transportwiderstände über einem Fichtenaltbestand im
Solling für den Zeitraum September 1997
-8-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
4.2 Verdunstete Wassermenge
Die Umrechnung der latenten Wärmeströme in einen Massenfluss ergab für den Monat
September ausgeprägte Tagesgänge (s.Abb.2). Die verdunstete Wassermenge ist nachts am
geringsten, für die Messwerte aus der Eddy-Covarianz-Methode (grün) und der Berechnung
nach Penman-Monteith (rot) liegt sie bei etwa 0,007 bzw. 0,003 kg/(h*m2), die berechnete
potentielle Verdunstung (blau) liegt durchschnittlich bei etwa 0,15 kg/(h*m2). Ab 6:30 Uhr
folgt für alle drei Berechnungen ein Anstieg bis zu einem Maximum gegen 14 Uhr. Die rote
Linie erreicht eine Verdunstung von ca. 0,13, die grüne ca. 0,17 und die blaue ca. 0,58
kg/(h*m2).
Abbildung 2: Der mittlere monatliche Tagesgang der verdunsteten Wassermenge in kg/(m²h) über einem
Fichtenaltbestand im Solling für den Zeitraum September 1997 nach verschiedenen Berechnungen
Nach Erreichen des Maximums fallen die rote und grüne Linie bis 17:30 Uhr relativ stark ab.
Die Berechnung nach Penman-Monteith erreicht ihr Minimum von ca. 0.003 kg/(h*m2)
schon um 18 Uhr, die Berechnung aus den Eddy-Kovarianz-Werten fällt langsamer ab und ist
erst gegen ca. 22 Uhr auf ihrem Minimalwert von 0,007 kg/(h*m2). Die Potentielle
-9-
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
Verdunstung fällt langsamer ab. Selbst im Laufe der Nacht geht die Verdunstung noch
langsam zurück, und hat ihr Minimum erst gegen 5:30 Uhr erreicht.
4.3 Bowensverhältnis
Abbildung 3: Das auf drei verschiedene Weisen berechnete Bowensverhältnis über einem Fichtenaltbestand im
Solling für den Zeitraum September 1997
Betrachtet man den mittleren monatlichen Tagesgang der drei Bowensverhältnisse so wird
deutlich, dass sich das mit Hilfe der potentiellen Evapotranspiration berechnete Verhältnis
(bowen_pot) stark von den beiden anderen Verhältnissen unterscheidet. Ein Tagesgang ist in
dieser Darstellungsform nur schwer zu erkennen, es variiert nur wenig um 0. Lediglich
zwischen 5:30 und 18 Uhr sind leicht erhöhte Werte zu erkennen. Die beiden anderen
Verhältnisse weisen dagegen einen deutlichen Tagesgang auf. Das mit der Eddy-CovarianzMethode bestimmte Verhältnis (bowen_eddy) nimmt von 0 bis 5:30 Uhr Werte um -10 an.
Anschließend steigt es stark auf Werte von etwa 1 an und nimmt dann ab 17:30 Uhr wieder
auf Werte von ca. -7 ab. Das nach der Penman-Monteith berechnete Verhältnis (bowen_PM)
schwankt von 0 bis 5:30 Uhr um -25 und steigt anschließend auf Werte von etwa 2 an. Ab
- 10 -
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
17:30 Uhr kommt es auch hier zu einem starken Abfall der Werte, die um 24 Uhr rund -20
betragen. Interessanterweise weist das nach Penman-Monteith berechnete Verhältnis
wesentlich größere Schwankungen auf, als das nach den gemessenen Werten berechnete. Um
2:30 Uhr weisen beide Verhältnisse ein lokales Maximum auf.
- 11 -
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
5. Diskussion
5.1 Transportwiderstände
Der aerodynamische Transportwiderstand und der Grenzschichtwiderstand sind im Gegensatz
zum stomatären Transportwiderstand für die Verdunstungsrate fast unbedeutend klein.
Die Luft hat schon bei sehr geringer Wasserdampfuntersättigung ein sehr stark negatives
chemisches Potential von mehreren Mpa, sehr viel höher als das des Bodens oder auch des
pflanzlichen Gewebes. Um diesem enormen Potentialgefälle entgegenzuwirken regeln die
Pflanzen mithilfe der Spaltöffnungen, wieviel Transpiration sie zu Assimilationszwecken
zulassen. Dieser Mechanismus ist sehr wirkungsvoll und erlaubt den Pflanzen überhaupt erst
ein Überleben auf dem Land. Der ausgeprägte Tagesgang des Widerstandes rührt daher, dass
die Pflanzen bei entsprechendem Lichtangebot ihre Stomata öffnen um den Gasaustausch
(CO2) zu Photosynthesezwecken zuzulassen. Dadurch ist der Widerstand tagsüber geringer
als nachts und die Verdunstungsrate höher. Nachts schließen sich die Schließzellen, da kein
Licht für die Photosynthese vorhanden ist und die Verdunstung (wie im ürbigen auch
tagsüber) möglichst gering gehalten werden muss. Der Widerstand erreicht dort seinen
Maximalwert, und eine Verdunstung findet nur noch über die Cuticula statt. Daher wird der
Maximalwert auch als cuticulärer Widerstand bezeichnet. Die cuticulären Widerstände
unterscheiden sich von Pflanzenart zu Pflanzenart, je nach Ausbildung entsprechender
Schutzmechanismen. Die xerophilen Arten trockener Gebiete haben oftmals einen höheren
Cuticulawiderstand durch Wachsüberzüge und andere anatomische Besonderheiten. Ein
höherer Grenzschichtwiderstand wird durch die Ausbildung von Blatthärchen erreicht.
In unserer Betrachtung für den Monat September zeigt sich ein U-förmiger Verlauf für den
Stomatawiderstand. Die Ergebnisse der Berechnung könnten in der Wirklichkeit und
besonders in den heißen Sommermonaten anders aussehen, denn in der Mittagshitze würde
sich der Widerstand erhöhen, um einer zu starken Austrocknung der Pflanzengewebe
entgegenzuwirken. Jedoch würde er nicht bis auf seinen Maximalwert ansteigen, denn dann
wäre keine Photosynthese möglich und die kühlende Wirkung der Verdunstung würde
ebenfalls nur eingeschränkt zur Geltung kommen. Neben der Parametriesierung nach Wesley
bestehen noch viele andere Ansätze, die alle unterschiedliche Ergebnisse liefern. Das
Widerstandsmodell wurde nur aus Gründen der einfachen Handhabung gewählt, und ist in
seiner Form zu verallgemeinernd als dass gesicherte Erkenntnisse über den wahren
Stomatawiderstand aus ihr gewonnen werden können.
- 12 -
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
5.2 Verdunstete Wassermenge
Die Werte der potentiellen Verdunstung sind plausibler Weise sehr viel höher als die Werte
der Berechnungen mit gehinderter Wassernachlieferung. Der einzige Unterschied in der
Berechnung der Verdunstungsmenge nach Penman-Monteith ist im Gegensatz zur
potentiellen Verdunstung das Einbeziehen des stomatären Widerstandes. Hier zeigen sich die
enormen Auswirkungen der Spaltöffnungsregulierung. Würden sich die Spaltöffnungen
tagsüber nicht öffnen wären die Unterschiede zwischen aktueller und potentieller
Verdunstung noch größer. Der ähnliche Verlauf der mit der Eddy-Covarianz-Methode
gemessenen und der nach Penman-Monteith berechneten aktuellen Verdunstung zeigt, dass
der Ansatz der Annäherung des latenten Wärmestroms über die Energiebilanz brauchbar ist.
Die gemessenen Verdunstungsraten sind jedoch geringfügig höher, was darauf schließen lässt,
das der wahre stomatäre Widerstand wohl geringer als der berechnete eingeschätzt werden
muss. Die Wirkung des berechneten Widerstandes zeigt sich in Abbildung 2 sehr schön in der
Zeit von 17:30 bis 22 Uhr. Dort ist die berechnete Verdunstungsrate bereits auf ihrem
Minimalwert, wohingegen die gemessene nur langsam abfällt und erst gegen 22 Uhr ihren
Minimalwert erreicht hat. Dieser Unterschied lässt sich wie folgt erklären: Die Einstrahlung
liegt im monatlichen Mittel ab 19:00 Uhr unter 50 W/m2, dadurch wird der Widerstand
maximal (s. Abb.1) und die berechnete Verdunstung geht auf ihren Minimalwert zurück bis
die Einstrahlung morgens wieder auf über 50 W/m2 ansteigt. Die Messwerte aus der EddyCovarianz-Methode gehen jedoch sehr viel langsamer zurück, da immer noch geringfügige
Strahlung vorhanden ist und auch aus dem Bodenwärmestrom Energie zur Verdunstung
bereitgestellt wird, so dass diese Reihe erst um 22 Uhr ihr nächtliches Niveau erreicht hat.
5.3 Bowensverhältnis
Der wesentlich geringere Tagesgang des potentiellen Bowensverhältnisses im Vergleich zu
den beiden anderen Varianten lässt sich mit der Tatsache erklären, dass die potentielle
Verdunstung immer wesentlich größer ist als die reale. Kleine Werte der Evaporation führen,
dazu, dass der Nenner des Bruchs kleiner wird und somit der gesamte Wert des Bruchs
größer. Die leicht erhöhten Werte zwischen 5:30 und 18:30 Uhr können durch eine stärkere
Abgabe von fühlbarer Wärme erklärt werden. Da die Werte jedoch nicht größer als 1 werden
ist die potentielle Verdunstung immer größer als der fühlbare Wärmestrom.
Die stark negativen Werte des nach Penman-Monteith berechneten Verhältnisses von 0 bis 6
Uhr lassen sich auf verschieden Weise erklären. Zum einen könnte die Luft wärmer als der
Boden sein, so dass Energie von der Luft an den Boden abgegeben wird. Eine andere
- 13 -
Kommentar: Ich habe mich
erdreistet die Uhrzeit auf 19:00 Uhr
zu ändern.
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
Erklärungsmöglichkeit wäre Taubildung, bei dieser wird durch die Kondensation der
Wassermoleküle Energie in das System befördert. Zudem könnten auch starke Niederschläge
Energie in das System befördern. Da λE von der Strahlungsbilanz und dem
Bodenwärmestrom abhängig ist, nimmt es negative Werte an, wenn der BodenBestandeswärmestrom größer als die Nettostrahlung ist. Ein starker Bodenwärmestrom sollte
also auch als Erklärung in Betracht gezogen werden. Die anschließenden positiven Werte
deuten darauf hin, dass das System Energie nach oben abgibt. Da die Werte nach der PenmanMonteith-Berechnung sogar größer als 1 werden, überwiegt in diesem Zeitraum die
Energieabgabe in Form von fühlbarer Wärme. Die folgenden negativen Werte lassen sich mit
den oben bereits erwähnten Überlegungen erklären.
Der Tagesverlauf des mit der Eddy-Covarianz-Methode berechneten Verhältnisses weist
geringere Schwankungen auf und erreicht auch keine Werte >1. Dieses lässt sich wieder mit
der Tatsache erklären, dass die berechneten Widerstände größer als die tatsächlichen sind.
Größere Werte für die Widerstände führen zu einer Erniedrigung von λE und dieses zu einer
Erhöhung des Verhältnisses, also zu deutlicheren Schwankungen im Tagesverlauf.
Das lokale Minimum der beiden letztgenannten Tagesverläufe könnte durch Wind erklärt
werden. Der Wind führt zu einer Erniedrigung der Widerstände und somit zu einer Erhöhung
der Evaporation. Eine erhöhte Evaporation wiederum führt zu einer Verkleinerung des
Bowensverhältnisses.
Für den betrachteten Zeitraum scheint es realistisch, dass die negativen Werte für die Nächte
vor allem durch Taubildung hervorgerufen werden. Nachts kühlt sich die Lufttemperatur so
stark ab, dass sie weniger Feuchte halten kann. Die Fähigkeit Feuchtigkeit zu speichern ist
nämlich stark mit der Temperatur korreliert. Auch Niederschläge kommen in als Erklärung
für die negativen Werte in Frage. Bodenfrost scheint für den September unrealistisch.
6. Zusammenfassung
Mit Hilfe eines vorliegenden Datensatzes konnten Transportwiderstände, verdampfte
Wassermenge und das Bowensverhältnis berechnet werden. Dabei wurde deutlich dass sich
die potentielle Evaporation erheblich von der tatsächlichen unterscheidet. Zudem lies sich die
starke Bedeutung des stomatären Widerstandes für die Verdunstung zeigen. Desweiteren
wurden Unterschiede zwischen zwei verschiedenen Methoden zur Bestimmung der
Evaporation sichtbar, die sich auch auf das Bowensverhältnis auswirken.
- 14 -
Verdunstung
Paul Schmidt-Walter & Nikolas von Lüpke
7. Literatur
Häckel, H., 1999: Meteorologie, Verlag Eugen Ulmer, Stuttgart, 448 Seiten
Schulze, E.-D., Beck, E., Müller-Hohenstein, K., 2002: Pflanzenökologie, Spektrum
Akademischer Verlag, Heidelberg – Berlin, 846 Seiten
- 15 -