Gewinnmaximierung

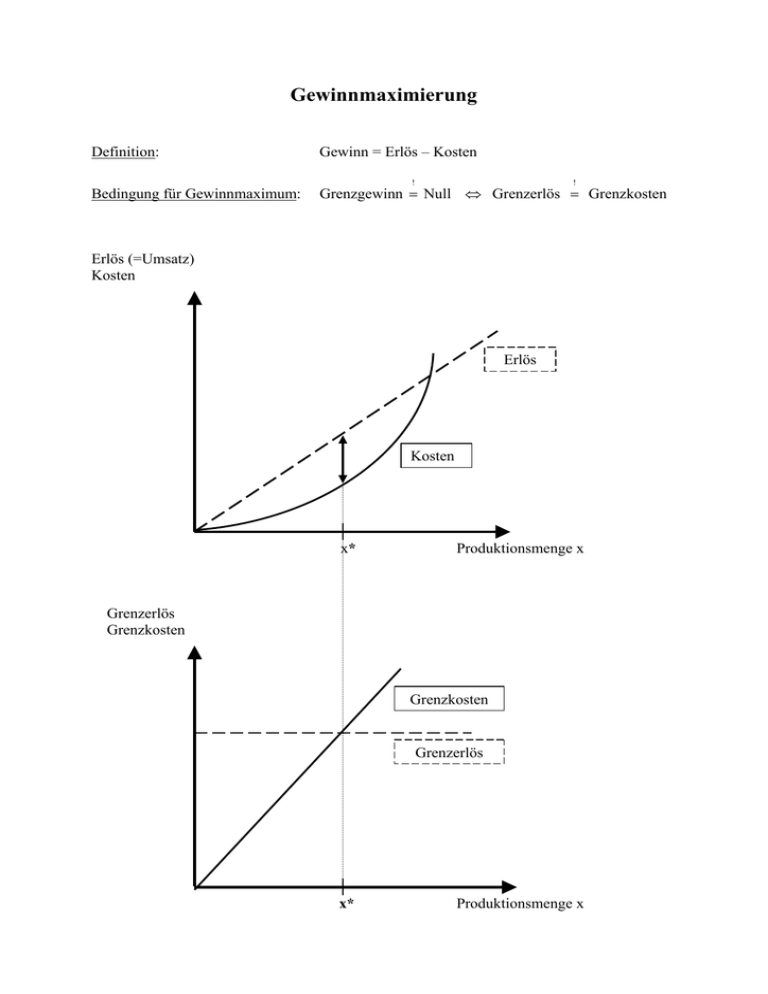
Gewinnmaximierung
Definition:
Gewinn = Erlös – Kosten
Bedingung für Gewinnmaximum:
Grenzgewinn = Null ⇔ Grenzerlös = Grenzkosten
!
!
Erlös (=Umsatz)
Kosten
Erlös
Kosten
x*
Produktionsmenge x
Grenzerlös
Grenzkosten
Grenzkosten
Grenzerlös
x*
Produktionsmenge x
Beispiel: Umsatz bzw. Erlös E ( x) = p ⋅ x und für einen Preis von z.B. p = 10 : E ( x) = 10 ⋅ x
K ( x) = x 2
Kosten
x
Absolute Werte
Erlös
Kosten
Gewinn
E(x)
K(x)
G(x)
0
0
0
0
1
10
1
9
2
20
4
16
3
30
9
21
4
40
16
24
5
50
25
25
6
60
36
24
7
70
49
21
Diskrete Änderungen
Marginale bzw. stetige Änderungen
+ E(x)
+ K(x)
+ G(x)
+10
+1
+9
+10
+3
+7
+10
+5
+5
+10
+7
+3
+10
+9
+1
+10
+11
-1
+10
+13
-3
E’(x) = p
K’(x) = 2x
G’(x)
x
+10
0
+10
0
+10
+2
+8
1
+10
+4
+6
2
+10
+6
+4
3
+10
+8
+2
4
+10
+10
0
5
+10
+12
-2
6
+10
+14
-4
7
Diskrete Betrachtung (Intervallskala)
Um welchen Betrag ändert sich der Gewinn, wenn die produzierte Menge um eine Einheit ( + x = 1 ) erhöht wird?
Man erkennt in der Tabelle:
Wird die produzierte Menge von vier auf fünf Mengeneinheiten erhöht, nimmt der Gewinn noch um eine Geldeinheit zu. Erhöht
man die produzierte Menge um eine weitere Einheit auf insgesamt sechs Mengeneinheiten, dann sinkt der Gewinn um eine
Geldeinheit.
Î Fünf Mengeneinheiten müssen optimal (=gewinnmaximal) sein!
Stetige Betrachtung (unendlich unterteilbare Skala)
Um welchen Betrag ändert sich der Gewinn, wenn die produzierte Menge marginal ( + x → 0 ) erhöht wird?
Man erkennt in der Tabelle:
Der Grenzerlös und die Grenzkosten stimmen bei fünf Mengeneinheiten überein, d.h. der Grenzgewinn ist null, wenn fünf
Mengeneinheiten produziert werden. Eine marginale Erhöhung der Menge (d.h. eine Erhöhung um eine unendlich kleine Einheit)
an dieser Stelle führt zu keinem weiteren Gewinnanstieg.
Î Fünf Mengeneinheiten müssen optimal (=gewinnmaximal) sein!
Die folgenden zwei Abbildungen stellen den Unterschied zwischen diskreter und stetiger Betrachtung grafisch am Beispiel der
2
Kostenfunktion K ( x) = x heraus. Ausgangspunkt ist die Menge x0 = 1 , d.h. im Ausgangspunkt produziert der Unternehmer genau
eine Mengeneinheit. Um welchen Betrag steigen nun die Kosten, wenn er von diesem Punkt ausgehend seine Produktionsmenge
erhöht?
Das linke Diagramm (diskrete Änderung) veranschaulicht den Kostenanstieg für genau eine weitere Mengeneinheit (die Kosten
steigen von 1 GE auf 4 GE, d.h. der Kostenanstieg beträgt 3 Geldeinheiten). Der Kostenanstieg bei diskreter Erhöhung der
Produktionsmenge entspricht somit dem Anstieg der Sekanten A.
Das rechte Diagramm (marginale bzw. stetige Änderung) veranschaulicht den Kostenanstieg für eine marginale, weitere
Mengeneinheit (d.h. die Kosten steigen im Punkt x0 = 1 entsprechend der Ableitung in diesem Punkt, d.h. um
K '(1) = 2 Geldeinheiten). Der Kostenanstieg bei stetiger Erhöhung der Produktionsmenge entspricht somit dem Anstieg der
Tangenten B.