n-Typ negative Spannung p-Typ Halbleiter in Sperrrichtung positive
Werbung

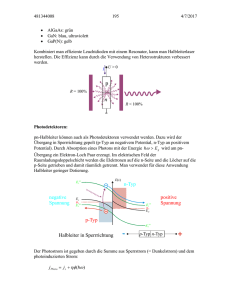
Festk0203_23 • • • 195 5/26/2003 AlGaAs: grün GaN: blau, ultraviolett GaP(N): gelb Kombiniert man effiziente Leuchtdioden mit einem Resonator, kann man Halbleiterlaser herstellen. Die Effizienz kann durch die Verwendung von Heterostrukturen verbessert werden. I U>0 p R = 100% n R < 100% Photodetektoren: pn-Halbleiter können auch als Photodetektoren verwendet werden. Dazu wird der Übergang in Sperrrichtung gepolt (p-Typ an negativem Potential, n-Typ an positivem Potential). Durch Absorption eines Photons mit der Energie hω > E g wird am pnÜbergang ein Elektron-Loch Paar erzeugt. Im elektrischen Feld der Raumladungsdoppelschicht werden die Elektronen auf die n-Seite und die Löcher auf die p-Seite getrieben und damit räumlich getrennt. Man verwendet für diese Anwendung Halbleiter geringer Dotierung. E(x) EL(p) negative Spannung EA µp(p) EV n-Typ EL(n) µn ED positive Spannung p-Typ (n) EV Halbleiter in Sperrrichtung p-Typ n-Typ Der Photostrom ist gegeben durch die Summe aus Sperrstrom (= Dunkelstrom) und dem photoinduzierten Strom: j Photo = j s + ηφ (hω ) Festk0203_23 196 5/26/2003 Hier bezeichnet µ die Quanteneffizienz (= nachgewiesene e-h+-Paare pro absorbiertes Photon) und φ (hω ) den Photonenfluss. Solarzellen: Bei Solarzellen wird der pn-Übergang grossflächig ausgebildet, damit möglichst viele Photonen in die Nähe des pn-Übergangs gelangen können. Der Photostrom führt zur Injektion von zusätzlichen Ladungen, die durch die Raumladungen an der Grenzschicht getrennt werden. 6 4 Solarzelle Strom 2 0 -2 Vopen Ishort ηφ (h (hω ) -4 -6 -4 -2 0 Vmax, Imax 2 4 Spannung 6 File Halbleiter.opj Wenn man die Kontakte kurzschliesst, fliesst der Kurzschlussstrom I short . Bei geöffnetem Kontakt ergibt sich die Leerlaufspannung U open . Die maximale Leistung kann von der Solarzelle entnommen werden, wenn sie geeignet belastet wird Pmax = f ⋅ I maxVmax f ist der Füllfaktor der Solarzelle (siehe auch Übungsaufgabe). hν p-Typ n-Typ 5.6.5. Weitere Halbleiterstrukturen Mit Hilfe von Epitaxieverfahren kann man Heterostrukturen aus verschiedenen Halbleitermaterialien herstellen. Wegen unterschiedlichen Energielücken entstehen Diskoninuitäten im Valenz- und Leitungsband. Festk0203_23 197 5/26/2003 E EL ∆EL EL1 Eg2 Eg1 µ1 EV1 µ2 ∆EV Bsp: GaAs 2 EV 2 Bsp: AlxGa1-xAs Technologisch wichtig ist zum Beispiel die Kombination von GaAs und AlxGa1-xAs. Sowohl Al als auch Ga haben 3 Valenzelektronen. Sie haben eine Gitterfehlanpassung von nur etwa 1%, aber stark verschiedene Energielücken: E gGaAs ≈ 1.4 eV , 1.4 < E gAlGaAs < 2.2 eV , je nach Aluminiumgehalt. Eine gute Gitteranpassung ist notwendig, damit an der Grenzfläche möglichst wenige Defekte entstehen. Damit kann man zum Beispiel 1- oder 2-dimensionale Quantentöpfe herstellen. AlxGa1-xAs AlxGa1-xAs GaAs E2 E1 E0 Bei einer Schichtdicke von d = 10 nm erhält man dann für die Quantisierung des Elektronengases in z-Richtung ∆k z = π d , während für die x- und y-Richtung die Quantisierung weiterhin bestimmt ist durch die Probengrösse, i.e. ∆k x = ∆k y = 2π / L , wobei L von der Grössenordnung cm ist. Damit Festk0203_23 198 5/26/2003 kann man sowohl Grundlagenforschung betreiben (z. B. Quantenhalleffekt) oder technische Anwendungen machen (Laser, Hochfrequenztransistoren etc.). In k x - und k y Richtung hat man parabolische Bänder, während in k z -Riochtung diskrete Zustände mit Energieniveaus bei E 0 , E1 etc. entstehen. ρ(E) E E2 E1/2 E0 E1 E2 E E prop. to kx,y 2 E1 E0 kx,y 5.7. Defekte in Gittern Bei der Diskussion der Halbleiter haben wir vorausgesetzt, dass die Fremdatome auf regulären Gitterplätzen des Diamantgitters eingebaut werden. Defekte sind in Kristallen wegen des Entropieterms in der freien Energie auch im thermischen Gleichgewicht vorhanden. Fehlstellen erhöhen die Entropie. Man unterscheidet • • Punktdefekte ( d = 0 ): Intrinsisch, Verunreinigungen, Dotierung Versetzungen ( d = 1 ): Es fehlt eine Linie von Atomen Versetzung • Korngrenzen, Grenzflächen, Stapelfehler, Zwillinge, Oberflächen ( d = 2 ): z.B. wenn man in eine Folge von dichtgepackten, hexagonalenen Ebenen einen Stapelfehler einfügt: abcabcabcabcabc ⇒ abcabcababcabc. Die folgende Figur zeigt als Beispiel eine Zwillingsstruktur. 2 Festk0203_23 199 5/26/2003 Zwillingsebene (113) Den Zwillingsbereich erhält man durch Spiegelung des einen Kristalls an der Zwillingsebene. Eigenschaften von Materialien werden nicht nur von den Eigenschaften des Kristalls, sondern auch von Defekten kontrolliert: Leitfähigkeit, Farbe von Kristallen, Lumineszenz, Magnetismus (Kondo-Effekt), mechanische Eigenschaften, Plastizität etc. Neueste Entwicklungen sind Nanokristalle. Wir besprechen hier nur kurz die Punktdefekte. Dazu gehören auch Dotierungen. Der einfachste Defekt ist der Schottky-Defekt. Er entspricht einem fehlenden Atom in der sonst regelmässigen Kristallstruktur. Man erhält ihn, indem man das Atom an die Oberfläche des Kristalls transportiert. In dichtgepackten Kristallstrukturen hat man in der Nähe des Schmelzpunkts typisch 10 −3 − 10 −4 Leerstellen. In harten Materialien wie TiC kann man bis zu 50% Fehlstellen haben. Schottky-Defekt Frenkel-Defekt Wenn man N Atome und n Fehlstellen hat, ist die Besetzungswahrscheinlichkeit für die Besetzung von n Stellen gegeben durch den Boltzmannfaktor n = e − E S / k BT . N −n Da n << N gilt ungefähr n ≅ Ne − ES / k BT . E S gibt an, wieviel Energie man braucht, um ein Atom von der Fehlstelle zur Oberfläche des Kristalls zu bringen. Für E S = 1 eV und T = 1000 K erhält man eine Konzentration von n ≈ 10 −5 . Beim langsamem Abkühlen Festk0203_23 200 5/26/2003 nimmt die Zahl der Fehlstellen ab. Wenn man den Kristall abschreckt, wird die Zahl der Fehlstellen grösser sein und nicht im thermodynamischen Gleichgewicht sein. Bei Ionenkristallen ist es energetisch günstiger, positiv und negativ geladene Fehlstellen gleichzeitig an die Oberfläche zu bringen, damit der Kristall elektrisch neutral bleibt. Man erhält dann für die paarweise Erzeugung von Fehlstellen n ≅ Ne − ESP /( 2 k BT ) . Ähnlich erhält man für die Kreation von Frenkeldefekten die Wahrscheinlichkeit n≅ NN 'e − EF /( 2 k BT ) . Hier bedeutet N die Anzahl der Gitterpunkte und N’ die Anzahl der Zwischengitterplätze. Die elektrische Leitung von Alkali- und Silberhalogenidkristallen basiert auf der Bewegung von Ionen und nicht von der der Elektronen. Damit sich Ionen bewegen können, müssen Fehlstellen vorhanden sein. kann nicht diffundieren kann diffundieren: mit Leerstelle möglich Bei Vorliegen eines Konzentrationsgradienten erhält man aufgrund des 1. Fick’schen Gesetzes die Gleichung J N = − D∇N . J N gibt die Zahl der Atome an, die pro cm2 und s durch eine Fläche diffundieren, D ist die Diffusionskonstante mit der Einheit cm2s-1 und N (in cm-3) gibt die Konzentration der diffundierenden Atome an. D hängt von der Temperatur ab und ist oft gegeben durch einen Ausdruck der Form D = D0 e − E / k B T . Typische Werte sind D0 ≈ 0.3 cm2s-1 und die Aktivierungsenergie E ≈ 1 meV. D kann mit Hilfe von Neutronenstreuung gemessen werden. Farbzentren: Reine Alkalihalogenid Kristalle (Isolatoren) sind normalerweise durchsichtig im sichtbaren Bereich. Dotiert man einen Alkalihalogenid-Kristall mit zuvielen Alkaliatomen,dann werden negative geladene Ionenfehlstellen erzeugt. Ein Festk0203_23 201 5/26/2003 Elektron kann dann in die Fehlstelle diffundieren. Die Farbe wird erzeugt durch elektrisch Dipolanregung des im Potentialtopf gefangenen Elektrons. Fehlstellen können auch durch Bestrahlung erzeugt werden (Neutronen, Ionen). e- Merke: Reines Silberbromid ergibt bei Belichtung kein Bild (Kodak).