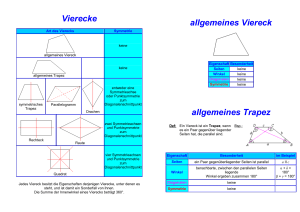
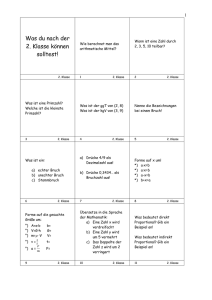
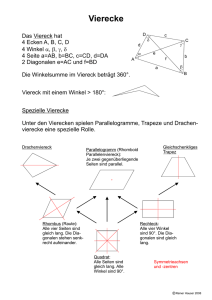
Viereck-Eigenschaften: Geometrie-Arbeitsblatt
Werbung
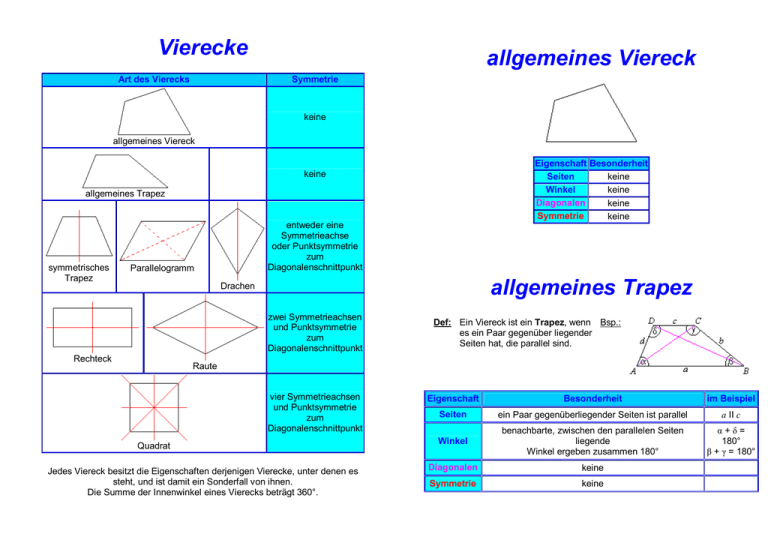
Vierecke Art des Vierecks allgemeines Viereck Symmetrie keine allgemeines Viereck Eigenschaft Besonderheit Seiten keine Winkel keine Diagonalen keine Symmetrie keine keine allgemeines Trapez symmetrisches Trapez entweder eine Symmetrieachse oder Punktsymmetrie zum Diagonalenschnittpunkt Parallelogramm allgemeines Trapez Drachen zwei Symmetrieachsen und Punktsymmetrie zum Diagonalenschnittpunkt Rechteck Def: Ein Viereck ist ein Trapez, wenn Bsp.: es ein Paar gegenüber liegender Seiten hat, die parallel sind. Raute vier Symmetrieachsen und Punktsymmetrie zum Diagonalenschnittpunkt Quadrat Jedes Viereck besitzt die Eigenschaften derjenigen Vierecke, unter denen es steht, und ist damit ein Sonderfall von ihnen. Die Summe der Innenwinkel eines Vierecks beträgt 360°. Eigenschaft Besonderheit im Beispiel Seiten ein Paar gegenüberliegender Seiten ist parallel a II c Winkel benachbarte, zwischen den parallelen Seiten liegende Winkel ergeben zusammen 180° α+δ= 180° β + γ = 180° Diagonalen keine Symmetrie keine symmetrisches Trapez Def.: Ein Viereck ist ein symmetrisches Bsp.: Trapez, wenn es ein Paar gegenüber liegender Seiten hat, die parallel sind und eine Symmetrieachse hat. Parallelogramm Def.: Ein Viereck ist ein Parallelogramm, wenn die gegenüber liegenden Seiten parallel sind. Bsp.: Eigenschaft Besonderheit im Beispiel Eigenschaft Besonderheit im Beispiel Seiten ein Paar gegenüberliegender Seiten ist parallel, das andere Seitenpaar ist gleich lang a II c b=d Seiten die gegenüber liegenden Seiten sind parallel und gleich lang a II c, a = c b II d, b = d α + δ = 180° β + γ = 180° α=β γ=δ Winkel Winkel benachbarte, zwischen den parallelen Seiten liegende Winkel ergeben zusammen 180°, benachbarte, an einer der parallelen Seiten liegende Winkel sind gleich groß die gegenüber liegenden Winkel sind jeweils gleich groß, die benachbarten Winkel ergeben zusammen 180° α=γ β=δ α + β = 180° β + γ = 180° γ + δ = 180° α + δ = 180° Diagonalen die Diagonalen halbieren sich Symmetrie keine Symmetrieachse, Punktsymmetrie zum Diagonalenschnittpunkt Diagonalen die Diagonalen sind gleich lang Symmetrie eine Symmetrieachse (durch die Mittelpunkte der parallelen Seiten) Gerade durch die Mittelpunkte von a und c Drachen Rechteck Def.: Ein Viereck ist ein Drachen, wenn es zwei Bsp.: Paare benachbarter Seiten hat, die jeweils gleich lang sind. Eigenschaft Besonderheit Def.: Ein Viereck ist ein Rechteck, Bsp.: wenn es vier rechte Winkel hat. im Beispiel Eigenschaft Besonderheit im Beispiel Seiten die gegenüber liegenden Seiten sind parallel und gleich lang a II c, a = c b II d, b = d α = β = γ = δ = 90° Seiten zwei Paare benachbarter Seiten sind jeweils gleich lang a=d b=c Winkel alle Winkel sind rechte Winkel Winkel zwei gegenüber liegende, zwischen den verschieden langen Seiten liegende Winkel sind gleich groß β=δ Diagonalen die Diagonalen halbieren sich und sind gleich lang Diagonalen die Diagonalen stehen senkrecht aufeinander und schneiden sich so, dass eine Diagonale halbiert wird (diejenige, die die Eckpunkte mit den gleich großen Winkeln verbindet) Symmetrie zwei Symmetrieachsen (die Verbindungslinien von den Mittelpunkten gegenüberliegender Seiten), Punktsymmetrie zum Diagonalenschnittpunkt Symmetrie eine Symmetrieachse (die nicht halbierte Diagonale) Raute (Rhombus) Quadrat Def.: Ein Viereck ist eine Raute Bsp.: (ein Rhombus), wenn es vier gleich lange Seiten hat. Def.: Ein Viereck ist ein Quadrat, wenn es Bsp.: vier gleich lange Seiten und vier rechte Winkel hat (regelmäßiges Viereck). Eigenschaft Besonderheit im Beispiel Eigenschaft Besonderheit im Beispiel Seiten alle Seiten sind gleich lang a=b=c=d Seiten a=b=c=d a II c, b II d die gegenüber liegenden Winkel sind jeweils gleich groß, die benachbarten Winkel ergeben zusammen 180° α=γ β=δ α + β = 180° β + γ = 180° γ + δ = 180° α + δ = 180° alle Seiten sind gleich lang und die gegenüber liegenden Seiten sind parallel Winkel alle Winkel sind rechte Winkel α = β = γ = δ = 90° Diagonalen die Diagonalen sind gleich lang, halbieren sich und stehen senkrecht aufeinander Symmetrie vier Symmetrieachsen (die Diagonalen und die Verbindungslinien von den Mittelpunkten gegenüberliegender Seiten), Punktsymmetrie zum Diagonalenschnittpunkt Winkel Diagonalen die Diagonalen halbieren sich und stehen senkrecht aufeinander Symmetrie zwei Symmetrieachsen (die Diagonalen), Punktsymmetrie zum Diagonalenschnittpunkt