Konfidenzintervall für Sigma
Werbung

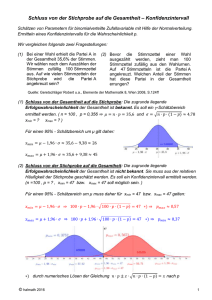
(c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Konfidenzintervall für Sigma Worum geht es in diesem Modul? Ausgangspunkt Chi^2-Verteilung Herleitung des Konfidenzintervalls Modifikation des Konfidenzintervalls Simulation: Konfidenzintervall für Sigma Breite des Konfidenzintervalls Worum geht es in diesem Modul? Aufbauend auf den bisher vorgestellten Konfidenzintervallen wird das Konfidenzintervall für (bzw. ) bei Normalverteilung nach dem bekannten Schema eingeführt. Parallel dazu wird die -Verteilung vorgestellt, die für das Kapitel "Testen" vorausgesetzt wird. Das Modul wird durch einen kurzen Ausblick auf Robustheitsaspekte bei Konfidenzintervallen abgeschlossen. Ausgangspunkt Als Einführung in die Konfidenzschätzung (s. ) haben wir das Konfidenzintervall für bei Normalverteilung hergeleitet. Dabei haben wir zunächst die Varianz als bekannt vorausgesetzt (um eine Vereinfachung der Herleitung zu erreichen), diese praxisfremde Annahme dann aber im folgenden Modul aufgegeben. Wie bereits angekündigt wollen wir uns nun dem zweiten Parameter der Normalverteilung, nämlich der Varianz , widmen. Die Herleitung des Konfidenzintervalls erfolgt dabei exakt nach dem gleichen Schema wie bisher. Wir wollen daher etwas abkürzen und gleich die Formel für das Konfidenzintervall für bei Normalverteilung bestimmen (auf die grafische Ableitung verzichten wir). Als Basis für die Ableitung wählen wir den Punktschätzer , der - wie wir bereits wissen - der Page 1 (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma unter Normalverteilung ist (vgl. ). Chi^2-Verteilung Um dem vertrauten Herleitungs-Schema folgen zu können, benötigen wir eine Zufallsvariable mit uns bekannter Verteilung, die enthält - dann können wir wieder eine entsprechende Wahrscheinlichkeitsaussage formulieren. Karl Pearson (1857-1936) und Friedrich Robert Helmert (1841-1917) Dazu machen wir davon Gebrauch, dass F. Robert Helmert (1876) und Karl Pearson (1900) die Wahrscheinlichkeitsverteilung der Zufallsvariablen hergeleitet haben, wobei die Zufallsvariable Stichprobe von unabhängig mit Erwartungswert normalverteilten Zufallsvariablen -Verteilung ("Chiquadrat"-Verteilung, Wahrscheinlichkeitsdichte Page 2 die empirische Varianz einer und Varianz ist. Die Verteilung von identisch heißt ist das griechische "Chi") und hat die (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma wobei der Parameter haben kann; - die Anzahl der Freiheitsgrade - die Werte ist die sog. "Gamma-Funktion". Für , und ist die Dichtefunktion in der Abbildung dargestellt. Dichtekurven der Chi^2-Verteilung für verschiedene Freiheitsgrade Weil nicht negativ sein kann, ist die Wahrscheinlichkeitsdichte der für negative Werte -Verteilung gleich null. Das hat auch zur Folge, dass die Verteilung nicht symmetrisch ist; allerdings nähert sie sich für der symmetrischen Glockenform der Normalverteilung. Mit Hilfe des folgenden Applet Chi-Verteilung (aa5.jar) kann die Dichte der -Verteilung in Abhängigkeit von den Freiheitsgraden betrachtet werden. Herleitung des Konfidenzintervalls Das weitere Vorgehen zur Gewinnung eines Konfidenzintervalls für entspricht unserem bisherigen Vorgehen bei der Ableitung der Konfidenzintervalle für Zunächst stellen wir das zentrale ( )-Schwankungsintervall für . auf: ; dabei sind )-Quantil der und das ( -Verteilung mit )-Quantil und das ( Freiheitsgraden. Eine Symmetriegleichung, die es uns gestattet, das ( )-Quantil durch das ( )-Quantil auszudrücken (wie bei ), gibt es wegen der fehlenden Symmetrie der -Verteilung nicht. Setzen wir in unsere letzte Gleichung ein, dann folgt , wobei ist. Würden wir den Ausdruck nach Page 3 auflösen, dann hätten wir ein zentrales (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Schwankungsintervall für müssen wir nach . Um ein Konfidenzintervall für zu bekommen, auflösen. Aus folgt , und aus folgt . Zusammengesetzt ergibt das . Die Grenzen des Intervalls für und in dieser Gleichung, , sind Zufallsvariablen; das zufällige Intervall zwischen ihnen überdeckt mit der Wahrscheinlichkeit die Varianz . Setzt man in die Gleichung für die Zufallsvariable den Stichprobenwert ein, dann erhält man die Grenzen und des konkreten Konfidenzintervalls für . Satz - Konfidenzintervall für bei Normalverteilung: Ist (d.h. Page 4 eine konkrete Stichprobe vom Umfang sind Realisierungen der Zufallsvariablen aus einer Normalverteilung , die (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma unabhängig identisch normalverteilt sind) mit unbekannter Varianz Stichprobenvarianz, dann ist und ist die mit und ein zweiseitiges Konfidenzintervall für und ( -Verteilung mit zum Konfidenzniveau )-Quantil und ( ; dabei sind )-Quantil der Freiheitsgraden. Modifikation des Konfidenzintervalls Wir haben ein Konfidenzintervall für die Varianz bei Normalverteilung hergeleitet. Aus der Punktschätzung wissen wir, dass neben der Varianz auch häufig nach der Standardabweichung - der Wurzel der Varianz - gefragt wird. Diese hat dieselbe Einheit wie die Realisierungen und ist daher besser zu veranschaulichen. Wir wollen deshalb auch das Konfidenzintervall für Normalverteilung bestimmen: bei Wenn wir in der Ungleichung die Wurzel ziehen, so dass in der Mitte steht, bleibt die Wahrscheinlichkeitsaussage unverändert. Daher ergibt sich ein zweiseitiges Konfidenzintervall für zum Konfidenzniveau sehr einfach aus dem entsprechenden Konfidenzintervall für . Das Konfidenzintervall für hat die Grenzen und mit . Beispiel: Streuung der Nettokaltmieten in Berliner Bezirken Page 5 mit (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma An dieser Stelle wird das Beispiel aus dem Modul aufgegriffen. Es ging um die Streuung der Nettokaltmieten für 2-Zimmer-Wohnungen in den Berliner Bezirken Zehlendorf und Neukölln. Folgende Daten standen zur Verfügung (Angaben in Euro): Zehlend 487 orf 650 582 714 1041 862 647 836 575 802 Neuköll 191 n 351 290 555 181 420 320 650 725 455 Die Stichprobenstandardabweichung hatten wir bereits ermittelt: und . Es sollen jetzt die Konfidenzintervalle zum Konfidenzniveau für die Mietpreise bestimmt werden. Dazu benötigen wir die Quantile der -Verteilung mit Freiheitsgraden: und . Einsetzen in ergibt für Zehlendorf . Für Neukölln erhalten wir entsprechend . Obwohl die Punktschätzwerte den Eindruck erwecken, dass die Mietpreise in Neukölln deutlich stärker streuen, wird anhand der Konfidenzintervalle deutlich, wie gering die Page 6 (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Präzision der Schätzung bei einem Stichprobenumfang von ist. Die Unterschiede könnten durchaus zufallsbedingt sein. Es wäre in jedem Fall sinnvoll, eine Nachziehung vorzunehmen, um den Stichprobenumfang (und damit die Präzision) zu vergrößern. Überlegungen zur Bestimmung eines adäquaten Stichprobenumfangs finden sich weiter unten . Beispiel: Kapitalmarkttheorie Im Rahmen der Kapitalmarkttheorie kommt der Bewertung der Risiken von Wertpapieren (Aktien, Derivaten, etc.) eine zentrale Rolle zu. Ein Maß für die Risikoträchtigkeit einer solchen Anlage ist die Standardabweichung (auch Volatilität genannt) der Renditen dieser Anlage. Eine hohe Volatilität impliziert dabei hohe Gewinnchancen und hohe Verlustrisiken gleichermaßen. Ob eine hohe Volatilität für einen Investor wünschenswert ist oder nicht, hängt von seinen Präferenzen, also seiner Risikobereitschaft, ab. Viele Kapitalmarktmodelle (z.B. das "Capital Asset Pricing Model", kurz: CAPM) unterstellen, dass die Renditen normalverteilt sind. Diverse empirische Untersuchungen (z.B. am DAX) konnten das allerdings nicht bestätigen. Sie deuten darauf hin, dass stattdessen die logarithmierten Renditen normalverteilt sind (sog. Log-Normal-Modell) oder eine Verteilung mit mehr Wahrscheinlichkeitsmasse in den Flanken ("long tailed") die Empirie besser abbildet. Der Einfachheit halber unterstellen wir im Folgenden dennoch normalverteilte Renditen. Zur Schätzung der Standardabweichung wurden die Renditen einer Aktie (bezogen auf einen Zeitraum von einem Tag) der letzten 250 Handelstage beobachtet. Es ergab sich . Wie hoch ist die Präzision dieser Schätzung beurteilt anhand des Konfidenzintervalls für zum Konfidenzniveau ? , ,,, Einsetzen in ergibt . Zum Konfidenzniveau 95% erhalten wir für unsere Renditenschätzung als Konfidenzintervall. Die Präzision der Schätzung liegt im Promille-Bereich. Die Kunden einer Spedition beschweren sich in letzter Zeit vermehrt über zu lange Transportzeiten ihrer Waren in die USA. Bisher wurde als einziges Maß zur Kontrolle der Transportzeit lediglich die mittlere Transportdauer beobachtet. Ein findiger Mitarbeiter kommt auf Idee, dass zwar möglicherweise die mittlere Transportdauer der gegenüber den Kunden kommunizierten ungefähren Transportzeit entspricht, es aber sehr starke Schwankungen gibt, die zu den Beschwerden führen. Um dies zu prüfen, soll ein Konfidenzintervall für die Standardabweichung der Transportzeit aufgestellt werden. Lösen Sie diese Aufgabe im Statistiklabor ( cf8.zmpf ). Simulation: Konfidenzintervall für Sigma Wir ziehen Stichproben vom Umfang aus einer Normalverteilung Page 7 und berechnen (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma jeweils das Konfidenzintervall für die Standardabweichung zum Konfidenzniveau und . k=100 Konfidenzintervalle für Sigma zum Konfidenzniveau 95% bzw. 99% (Stichproben vom Umfang n=10 aus N(50,10^2) Konfidenzniveau () Überdeckung (in %) Breite 95% 96% 11.04 99% 99% 16.11 Das vorgegebene Konfidenzniveau wird eingehalten. Wie erwartet, führt ein höheres Konfidenzniveau zu breiteren Intervallen (also zu geringerer Präzision der Schätzung). Mit der Breite der Konfidenzintervalle wollen wir uns im Folgenden ausführlicher beschäftigen. Die Simulation kann im Statistiklabor ( d54.spf ) nachvollzogen und modifiziert werden. Stellen Sie selbstständig im Statistiklabor ( d5b.zmpf ) eine Simulation an, in der sie die Übereinstimmung der empirischen Überdeckungshäufigkeit mit Konfidenzniveau untersuchen. Breite des Konfidenzintervalls Die absolute Breite des Konfidenzintervalls für , ist eine Zufallsvariable, weil S eine Zufallsvariable ist. Es ist leicht ersichtlich, dass ein höheres Konfidenzniveau (kleineres ) verkleinert und vergrößert. Dadurch wird in der Differenz der erste Wurzelterm größer und der zweite kleiner, so dass die erwartete Breite des Konfidenzintervalls zunimmt. Das bestätigt auch die Simulation . Die relative Breite, , wie auch die relativen Abstände der Konfidenzgrenzen von , und , sind aber keine Zufallsvariablen, d.h. die relative Präzision unserer Konfidenzaussage über hängt nur vom Stichprobenumfang und vom Konfidenzniveau ab. Daher ist es möglich, bei vorgegebenem Konfidenzniveau den Stichprobenumfang so festzulegen, dass einen vorgegebenen Wert nicht übersteigt, d.h. dass die obere Konfidenzgrenze für um nicht mehr als den Faktor von abweicht. Der Stichprobenumfang ergibt sich aus der Forderung oder , d.h. es ist so zu bestimmen, dass die Ungleichung erfüllt ist. Das folgende Beispiel erläutert die Berechnung. Beispiel: Stichprobenumfang bei vorgegebener relativer Präzision Der Stichprobenumfang soll so groß sein, dass die obere Grenze des Page 8 (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Konfidenzintervalls für zum Konfidenzniveau um nicht mehr als 30% größer ist als , dass also nicht mehr als das 1,3fache von beträgt. Es ist und daher ist das kleinste zu bestimmen, für das gilt. Da mit wachsendem wächst, berechnet man diesen Quotienten für , bis das ermittelt ist, für das die Ungleichung erfüllt ist. Daraus ergibt sich dann der gesuchte Stichprobenumfang als . Im vorliegenden Fall erhalten wir folgende Tabelle: Relation 1 0.001 0.5917 2 0.051 0.5917 3 0.216 0.5917 ... ... 34 0.583 0.5917 35 0.588 0.5917 36 0.593 0.5917 ... ... Für ergibt sich erstmals ein Wert, der größer ist als . Also ist der gesuchte Stichprobenumfang . Wir wollen das Ergebnis durch eine Simulation untermauern und ziehen dazu 5 Stichproben vom Umfang aus einer Normalverteilung . 5 Konfidenzintervalle für Sigma zum Konfidenzniveau 95% (Stichproben vom Umfang n=37 aus N(50,10^2) Wir prüfen anhand des ersten Konfidenzintervalls, ob die Vorgaben bzgl. relativer Abstände der Konfidenzgrenzen von eingehalten wurden: Page 9 12.396 7.761 9.543 9.543 1.299 0.813 (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Wie wir sehen, ist die relative Abweichung der oberen Intervallgrenze mit - wie gefordert - kleiner als 30%. Es wird außerdem deutlich, dass wir die untere Grenze vernachlässigen können, weil sie durch die asymmetrische Form des Konfidenzintervalls immer näher an liegt als . Im Beispiel haben wir bereits Konfidenzintervalle für die Standardabweichung der Nettokaltmieten in den Berliner Bezirken Zehlendorf und Neukölln aufgestellt und festgestellt, dass die Präzision der Intervallschätzung nicht unseren Anforderungen entsprach. Die obere Intervallgrenze wich um 82,6% vom entsprechenden Punktschätzwert bzw. ab. Wir wollen die relative Abweichung auf 10% begrenzen. Wie groß muss der Stichprobenumfang mindestens gewählt werden? Hinweis: Die Lösung erhält man durch Probieren, wenn man die Quantile der -Verteilung in einer Tabelle nachschlägt oder automatisiert mit Hilfe des Statistiklabors ( f68.zmpf ) . Dem Robustheitsaspekt haben wir im Rahmen der Punktschätzung ein eignes gewidmet. Wie wir festgestellt haben, ist die Robustheit eines Schätzers für die Forschungspraxis eine ganz wesentliche Eigenschaft. Daher soll an dieser Stelle exemplarisch die Robustheit eines Intervallschätzers thematisiert werden. Wir beschränken uns darauf zu untersuchen, wie das Konfidenzintervall für auf einzelne in die Stichprobe eingestreute Extremwerte reagiert, wie sie z.B. durch Mess-, Eingabe- oder Übertragungsfehler entstehen können. Zur Generierung der verschmutzen Stichproben verwenden wir das aus dem Modul Robustheit bekannte Verfahren: Wir ziehen Stichproben vom Umfang aus einer Normalverteilung. Nach einem Zufallsverfahren wird im Durchschnitt eine der 10 Beobachtungen in jeder Stichprobe ausgewählt und durch einen Wert, der um ca. abweicht, ersetzt. k=100 Konfidenzintervalle für Sigma aus "verschmutzen" Stichproben vom Umfang n=10 aus N(50, 10^2), Verschmutzungsgrad ca. 10% Obwohl im Durchschnitt jede Stichprobe nur einen Extremwert enthält, überdecken nur noch 35% der Intervalle (Breite 17.18) das wahre ; das Konfidenzniveau von wird bei weitem nicht eingehalten. Das Konfidenzintervall für ist ein besonders extremes Beispiel (wie wir wissen, ist auch kein robuster Schätzer für , vgl. ). Dennoch sollte die Robustheit auch bei Intervallschätzern nie vernachlässigt werden. Eine Verletzung der Modellannahmen kann bei Konfidenzintervallen zu einer Nichteinhaltung des Konfidenzniveaus führen, die bisweilen so extrem ausfallen kann wie in dieser Simulation. Nicht nur Extremwerte, sondern z.B. auch eine Verletzung der Verteilungsannahme oder der Unabhängigkeitsvoraussetzung kann derartige Folgen haben. Die Simulation kann im Statistiklabor ( fac.spf ) nachvollzogen und modifiziert werden. In diesem Modul haben wir ein Konfidenzintervall für (bzw.) unter Normalverteilung abgeleitet. Während die Breite des Konfidenzintervalls für eine Zufallsvariable ist, ist die relative Breite des Konfidenzintervalls eine Konstante. Die relative Breite erhält man durch Division der Breite durch den Schätzer . Analog ergeben sich die relativen Page 10 (c) Projekt Neue Statistik 2003 - Lernmodul: Konfidenzintervall für Sigma Abweichungen der Intervallgrenzen von als und. Durch diese Herangehensweise lässt sich der Stichprobenumfang so bestimmen, dass ein vorgegebener relativer Maximalabstand der oberen Intervallgrenze von nicht überschritten wird. Im Gegensatz zu den Konfidenzintervallen, die wir bisher kennengelernt haben, ist das Konfidenzintervall für nicht symmetrisch. Die obere Grenze des Intervalls weicht weiter vom Punktschätzwert ab als die untere. Im Rahmen der Herleitung des Konfidenzintervalls haben wir die -Verteilung kennengelernt, deren Quantile wir für die Bestimmung der Intervallgrenzen und benötigen. Die -Verteilung hat ebenso wie die t-Verteilung einen Parameter - die Anzahl der Freiheitsgrade, die sich aus ergeben. Die -Verteilung ist eine asymmetrische (genauer gesagt eine rechtsschiefe) Verteilung. Wie sich im Exkurs zur Robustheit gezeigt hat, ist das hergeleitete Konfidenzintervall wenig robust. Befinden sich Extremwerte in der Stichprobe, wird das Konfidenzintervall unbrauchbar, da das vorgegebene Konfidenzniveau nicht eingehalten wird. Um auch in derartigen Fällen solide Intervallschätzungen zu ermöglichen, könnte man z.B. ein Konfidenzintervall mit dem korrigierten bzw. (vgl. ) konstruieren. Mit diesem Modul werden unsere Betrachtungen zu Konfidenzintervallen für die Parameter der Normalverteilung abgeschlossen. Chi^2-Verteilung ErklärungKonfidenzintervall für Sigma ErklärungKonfidenzintervall für Sigma^2 ErklärungPräzision, relative Erklärung (c) Projekt Neue Statistik 2003, Freie Universität Berlin, Center für Digitale Systeme Kontakt: http://www.neuestatistik.de Page 11