Algorithmische Geometrie Thema: Konvexe Hüllen
Werbung

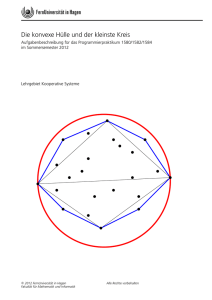
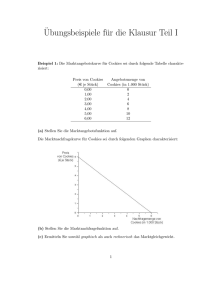
Algorithmische Geometrie Thema: Konvexe Hüllen Christoph Hermes [email protected] 17. Juni 2003 Ausblick auf den Vortrag • Was sind konvexe Hüllen? Wozu braucht man sie? • Wie kann man sie berechnen → gibt es Algorithmen? ? naiver Algorithmus: Einwickeln ? Graham Scan ? Quickhull • Wie kann man die Laufzeit verbessern? → innere Elimination • Fazit/ Demonstration 1/32 1 Was sind konvexe Hüllen? • mathematisch: definiert als das kleinste Polygon, dass alle Punkte enthält 2/32 2 Was sind konvexe Hüllen? • mathematisch: definiert als das kleinste Polygon, dass alle Punkte enthält • analog: kürzester Pfad, der alle Punkte umschließt 2/32 2 Was sind konvexe Hüllen? 2/32 • mathematisch: definiert als das kleinste Polygon, dass alle Punkte enthält • analog: kürzester Pfad, der alle Punkte umschließt • oder auch: Jede Linie, die zwei Punkte dieser Punktmenge verbindet, muss innerhalb des Polygons liegen 2 Wozu braucht man sie? • Datamining 3/32 3 Wozu braucht man sie? • Datamining • Computergraphik - Näherung für Objektgeometrie 3/32 3 Wozu braucht man sie? • Datamining • Computergraphik - Näherung für Objektgeometrie • Pathfinding 3/32 3 Einwickeln - graphisch • gegeben: Punktmenge P 4/32 4 Einwickeln - graphisch • gegeben: Punktmenge P • Suche den Punkt mit y = min 5/32 5 Einwickeln - graphisch • gegeben: Punktmenge P • Suche den Punkt mit y = min • Finde den kleinsten Winkel von der Horizontalen ausgehend 5/32 5 Einwickeln - graphisch • gegeben: Punktmenge P • Suche den Punkt mit y = min • Finde den kleinsten Winkel von der Horizontalen ausgehend • Suche den kleinsten Winkel zum nächsten Punkt 6/32 6 Einwickeln - graphisch • gegeben: Punktmenge P • Suche den Punkt mit y = min • Finde den kleinsten Winkel von der Horizontalen ausgehend • Suche den kleinsten Winkel zum nächsten Punkt • Fahre so lange fort, bis der Anfangspunkt wieder erreicht ist 7/32 7 Einwickeln - Bewertung 8/32 • Vorteil: Algorithmus lässt sich auch auf höhere Dimensionen erweitern 8 Einwickeln - Bewertung 8/32 • Vorteil: Algorithmus lässt sich auch auf höhere Dimensionen erweitern • Nachteil: Effizienz leidet erheblich NP −1 N 2−N Laufzeit: (N − i) = 2 ⇒ Θ(N 2) i=1 Das ist auch gleichzeitig Worst Case: O(N 2) 8 Einwickeln - Bewertung 8/32 • Vorteil: Algorithmus lässt sich auch auf höhere Dimensionen erweitern • Nachteil: Effizienz leidet erheblich NP −1 N 2−N Laufzeit: (N − i) = 2 ⇒ Θ(N 2) i=1 Das ist auch gleichzeitig Worst Case: O(N 2) • Es geht auch besser: Graham Scan (von R.L. Graham, 1972) 8 GrahamScan - graphisch • wieder gegeben: Punktmenge P mit A als Minimum und Pivot (A.y = min ∨ A.x = max) 9/32 9 GrahamScan - graphisch • wieder gegeben: Punktmenge P mit A als Minimum und Pivot (A.y = min ∨ A.x = max) • erzeuge ein einfaches Polygon 10/32 10 GrahamScan - graphisch • wieder gegeben: Punktmenge P mit A als Minimum und Pivot (A.y = min ∨ A.x = max) • erzeuge ein einfaches Polygon • A und B stehen schon als Teil der konvexen Hülle fest Beginne daher, ein Polygon ABC zu konstruieren 10/32 10 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D 11/32 11 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht 12/32 12 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 12/32 12 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 13/32 13 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 14/32 14 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 15/32 15 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 16/32 16 GrahamScan - graphisch • erzeuge eine neues Teilpolygon mit dem nächsten Punkt → hier D • backtracking: Eliminiere Punkte, bei denen die Hülle einen Knick nach rechts macht • wiederhole nun die letzten beiden Schritte so lange, bis das einfache Polygon abgearbeitet ist. Hier im Schnelldurchlauf. 17/32 17 GrahamScan - Pseudocode PointList GrahamScan(PointList ptLst) { ptLst = createSimplePolygon(ptLst); 18/32 // Erstelle ein einfaches Polygon 18 GrahamScan - Pseudocode 18/32 PointList GrahamScan(PointList ptLst) { ptLst = createSimplePolygon(ptLst); // Erstelle ein einfaches Polygon Point cur; for (int i=2; i<ptLst.len; i++) { // Durchlaufe Polygon mit Backtracking cur = ptLst[i-1]; while(turnRight(cur.Prev,cur,cur.Next)) { cur = cur.Prev; cur.Next.delete(); } } } 18 GrahamScan - Bewertung • eigentlicher Algorithmus läuft in linearer Zeit ab ⇒ Θ(N ) 19/32 19 GrahamScan - Bewertung • eigentlicher Algorithmus läuft in linearer Zeit ab ⇒ Θ(N ) • aber: das Sortieren erfordert Θ(N log N ) darum gesamt Θ(N log N ) 19/32 19 GrahamScan - Bewertung 19/32 • eigentlicher Algorithmus läuft in linearer Zeit ab ⇒ Θ(N ) • aber: das Sortieren erfordert Θ(N log N ) darum gesamt Θ(N log N ) • ein anderes Verfahren in der gleichen Effizienzklasse: Quickhull (analog zu Quicksort) 19 Quickhull - graphisch • Gegeben: Punktmenge P 20/32 20 Quickhull - graphisch • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften 21/32 21 Quickhull - graphisch • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons 22/32 22 Quickhull - graphisch 23/32 • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons • Verfahre genauso mit den neuen Grenzen bis keine neuen Punkte mehr zu finden sind 23 Quickhull - graphisch 24/32 • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons • Verfahre genauso mit den neuen Grenzen bis keine neuen Punkte mehr zu finden sind 24 Quickhull - graphisch 25/32 • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons • Verfahre genauso mit den neuen Grenzen bis keine neuen Punkte mehr zu finden sind 25 Quickhull - graphisch 26/32 • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons • Verfahre genauso mit den neuen Grenzen bis keine neuen Punkte mehr zu finden sind 26 Quickhull - graphisch 27/32 • Gegeben: Punktmenge P • Suche zwei Punkte, die garantiert auf der konvexen Hülle liegen und teile die Punkte dementsprechend in zwei Hälften • Finde den Punkt mit dem größten Abstand von der Teilungslinie und elimiere Punkte innerhalb des neuen Polygons • Verfahre genauso mit den neuen Grenzen bis keine neuen Punkte mehr zu finden sind und verbinde den Rest zu einem Polygon 27 Quickhull - Bewertung • Effizienz wie bei Quicksort: Θ(N log N ) 28/32 28 Quickhull - Bewertung 28/32 • Effizienz wie bei Quicksort: Θ(N log N ) aber mit Worst Case: O(N 2) (wenn alle Punkte auf der konvexen Hülle liegen) 28 Quickhull - Bewertung 28/32 • Effizienz wie bei Quicksort: Θ(N log N ) aber mit Worst Case: O(N 2) (wenn alle Punkte auf der konvexen Hülle liegen) • Im direkten Vergleich zum GrahamScan und WrapAlgorithmus das schnellste Verfahren in der praktischen Anwendung 28 Quickhull - Bewertung 28/32 • Effizienz wie bei Quicksort: Θ(N log N ) aber mit Worst Case: O(N 2) (wenn alle Punkte auf der konvexen Hülle liegen) • Im direkten Vergleich zum GrahamScan und WrapAlgorithmus das schnellste Verfahren in der praktischen Anwendung • lässt sich auch auf die dritte Dimension anwenden 28 innere Elimination 29/32 • Verbesserung des GrahamScan´s und der naiven Hülle? Sicherlich kann man an den Konstanten ein wenig ”rütteln”, aber was ist mit der Anzahl der Punkte an sich? 29 innere Elimination 29/32 • Verbesserung des GrahamScan´s und der naiven Hülle? Sicherlich kann man an den Konstanten ein wenig ”rütteln”, aber was ist mit der Anzahl der Punkte an sich? • Lösung: Vorberechung mit der ”inneren Elimination” 29 innere Elimination - Verfahren gegeben: Punktmenge P 30/32 30 innere Elimination - Verfahren → gegeben: Punktmenge P Suche vier Extrempunkte und bilde daraus ein rechteckähnliches Polygon 30/32 30 innere Elimination - Verfahren → gegeben: Punktmenge P 30/32 → Suche vier Extrempunkte und bilde daraus ein rechteckähnliches Polygon Bilde in dem Polygon ein Rechteck und eliminiere die darin enthaltene Punkte 30 innere Elimination - Bewertung • Effizienz: Θ(N ) 31/32 31 innere Elimination - Bewertung • Effizienz: Θ(N ) √ • Es bleiben N Punkte im Schnitt übrig (lt. stochastischer Geometrie) 31/32 31 innere Elimination - Bewertung • Effizienz: Θ(N ) √ • Es bleiben N Punkte im Schnitt übrig (lt. stochastischer Geometrie) • Eliminationsverfahren schon in Quickhull enthalten 31/32 31 Fazit 32/32 • Welchen der bisher dargestellten Algorithmen sollte man nun bevorzugen? 32 Fazit 32/32 • Welchen der bisher dargestellten Algorithmen sollte man nun bevorzugen? • Ist die Wahrscheinlichkeit groß, dass Punkte schon auf einer konvexen Hülle liegen: innere Elimination + GrahamScan 32 Fazit 32/32 • Welchen der bisher dargestellten Algorithmen sollte man nun bevorzugen? • Ist die Wahrscheinlichkeit groß, dass Punkte schon auf einer konvexen Hülle liegen: innere Elimination + GrahamScan • sonst: Quickhull 32 Fazit 32/32 • Welchen der bisher dargestellten Algorithmen sollte man nun bevorzugen? • Ist die Wahrscheinlichkeit groß, dass Punkte schon auf einer konvexen Hülle liegen: innere Elimination + GrahamScan • sonst: Quickhull ⇒ Und das Beste zum Schluss: Die Demonstration 32 Literatur zum Nachschlagen • R. Sedgewick: Algorithmen in C, Kap. 24/25 • Java-Applets: I http://www.cs.princeton.edu/ ah/ alg anim/version1/GrahamScan.html I http://www.pms.informatik.uni-muenchen.de/ lehre/compgeometry/Gosper/convex hull/ applet/convex hull applet.html • Ansonsten hilft meistens googlen :)