M9 Kurzfassung Trigonometrie Erinnerung: Kongruenzsätze SSS

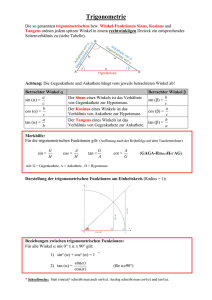
M9 Kurzfassung Trigonometrie
Erinnerung: Kongruenzsätze SSS, SWS, WSW, SsW
Wiederhole eigenständig: elementare Konstruktionen nach diesen Sätzen
Grundwissen: Elementare Sätze über Dreiecke:
o
o
o
o
Winkelsumme 1800
Dreiecksungleichung
Alle Dreiecke haben Umkreis und Inkreis
Alle Mittelsenkrechten, Winkelhalbierenden, Höhen, Seitenhalbierende
schneiden sich in je einem Punkt M, W, H, S
Dreiecke, die in den Angaben SSS, SWS, WSW, SsW übereinstimmen, sind damit
o kongruent und
o eindeutig konstruierbar → Elementarkonstruktionen
Da die Dreiecke aus je drei Daten eindeutig konstrierbar sind,
sollte es möglich sein, die restlichen Daten zu berechnen … Das geht tatsächlich!
Vorweg: „Ähnlichkeit“
Etwas salopp:
Kongruenz = gleiche Form und Größe
Ähnlichkeit = gleiche Form
Überlege:
WWW ist kein Kongruenzsatz!
WWW liefert nur ähnliche Dreiecke Δ1 und Δ2: α1 = α2 , β1 = β2 , γ1 = γ2
Für ähnliche Dreiecke Δ1 und Δ2 gilt nach dem Strahlensatz: a1:a2 = b1:b2 = c1:c2
Rechtwinklige Dreiecke
Rechtwinklige Dreiecke sind über die Sätze von Pythagoras berechenbar!
Dem rechten Winkel gegenüber: die Hypotenuse h
Betrachte die Winkel φ und φ´
Und die Gegenkathete g gegenüber φ
sowie die Ankathete a als zweiten Schenkel von φ
Mit den Mitteln höherer Mathematik sind die Seitenverhältnisse g/h und a/h direkt mit
beliebiger Genauigkeit berechenbar.
Alle TR und Computerprogramme verfügen über entspr. Algoritmen.
StD F.Sl 2010
1/5
2/5
M9 Kurzfassung Trigonometrie
Aus formalen Gründen → werden folgende sinnvollen Bezeichnungen und Schreibweisen
benutzt:
g : h = SINUS von φ = sin (φ) = auch kurz sin φ
a : h = COSINUS von φ = cos (φ) = auch kurz cos φ
Der Vollständigkeit halber definiert man noch
g : a = TANGENS von φ = tan (φ) … auch tan φ oder tg φ
Gut einprägen: Sinus (Winkel) = Gegenkathete : Hypotenuse
Cosinus (Winkel) = Ankathete : Hypotenuse
Tangens (Winkel) = Gegenkathete : Ankathete
Gut einprägen: Gegenkathete = Hypotenuse · Sinus (Winkel)
Ankathete = Hypotenuse · Cosinus (Winkel)
Gegenkathete = Ankathete · Tangens (Winkel)
0
Überlege – eine erste Regel: sin φ = cos φ´ = cos (90 –φ)
Überlege – eine zweite Regel: tan φ = sin φ / cos φ
Zeige – ein wichtiges Gesetz: (sin φ) ² + (cos φ) ² = 1
Überlege (derzeit noch) 00 < φ < 900
0 < sin φ < 1
und 1 > cos φ > 0 und 0 < tan φ < ∞
Aufgabe:
Berechnung spezieller Werte der sog. Winkelfunktionen sin, cos, tan
für die Argumente φ = 00 , 300 , 450 , 600
Merken (Eselsbrücke):
sin (300) = ½·
sin (450) = ½ ·
sin (600) = ½ ·
sin (900) = ½ ·
1 =½
2
3
4 =1
Beliebige Werte werden mit dem TR berechnet … sin ( 500) = 0,766044443 …
StD F.Sl 2010
3/5
M9 Kurzfassung Trigonometrie
Betrachte nun sin φ , cos φ und tan φ als Funktionen des Winkels φ
…
Da bislang alle Funktionen als sog Argument (Variable) ein dimensionsloses x benutzen,
führt man eine dimensionslose Winkelgröße ein …
Eine neue Winkelgröße: der ARCUS
Für einen Winkel beliebiger Größe definieren wir
Auswendig lernen:
Der ARCUS von φ = arc (φ)
ist die dimensionslose Länge des Bogens zu diesem Winkel in einem Kreis mit Radius 1.
Auswendig lernen:
der arcus eines Winkels ist die Länge des Bogens in einem Kreis mit Radius 1
Prüfe, ob du das verstanden hast:
arc ( 3600 ) = 2π = 6, 28…
arc ( 1800 ) = π = 3,14 …
arc ( 900 ) = π/2
arc ( 600 ) = π/3
arc ( 450 ) = π/4
Dein Rechner kann den Winkel in „GRAD“ ( deg) und im Arcus ( arc) verarbeiten.
Überlegen und merken: arc(φ) / π = φ/1800
Einprägen:
arc (3600) = 2π ; arc (1800) = π ; arc (900) = π/2 ; arc (600) = π/3 ; arc (450) = π/4
0
Formel: arc (φ) : 2π = φ : 360
0
bzw. arc (φ) : π = φ : 180
In einem Einheitskreis ( Radius = 1 ) lassen sich Arcus und die Winkelfunktionen elegant
gegenüberstellen.
y 11
Die Winkelfunktionswerte sind direkt als Längen
der Kathteten greifbar !
10
9
8
Der Arcus ist die Länge des Bogens zu α
7
6
Ausgehend vom Einheitskreis kann man die
Winkelfunktionen problemlos auf Winkel > 900
erweitern …
5
4
3
2
90 °
1
-1

1
1
2
3
4
5
6
7
8
9
10
x
11
12
Wir definieren sie einfach als Streckenlängen der
Katheten !
-1
-2
Damit sind sin (x) , cos (x) und tan (x) Funktionen auf R mit der Variable x als Arcus des
Winkels.
StD F.Sl 2010
4/5
M9 Kurzfassung Trigonometrie
Erweiterung der Winkelfunktionen: Winkel > 900
Die elementaren Definitionen im rechtwinkligen Dreieck
 Sinus (Winkel) = Gegenkathete : Hypotenuse
 Cosinus (Winkel) = Ankathete : Hypotenuse
 Tangens (Winkel) = Gegenkathete : Ankathete
dienen naturgemäß vorrangig Berechungen in rechtwinkligen Dreiecken …
Man kann darauf aufbauend Algorithmen für bel. Dreiecke entwickeln (Sinus-, Cosinussatz)
Mit einem genialen Trick kann man die Einschränkung 00 < Winkel < 900 überwinden –
Und man erhält ein wertvolles in Wissenschaft und Technik vielbenutztes Werkzeug …
Du brauchst dieses Werkzeug u.a. für die Beschreibung von Kreis- und Schwingbewegungen!
Die Winkelfunktionen im Einheitskreis
Wir betrachten Sinus, Cosinus, Tangens
als FUNKTIONEN des Winkels.
Dieser Winkel (Das Argument, die Variable
der Funktion) wird i.a. als reine Zahl …
als ARCUS angegeben !
Die Werte der Funktionen sind direkt auf den
Achsen ablesbar.
Beachte die Vorzeichen!
Damit erhält man periodische Graphen …
Diese Graphen beschreiben viele
Präge sie dir gut ein !
f(x) = sin (x)
f(x) = cos (x)
Wichtig: die Winkelfunktionen sin x , cos x haben die „Periode“ 2π
StD F.Sl 2010
5/5
M9 Kurzfassung Trigonometrie
Die allgemeine Winkelfunktion A · sin[2π/p · (x + Δφ)] + c
Variiere die Parameter in einem Kurvenplotter …
Paramter und Darstellung gemäß der üblichen Schreibweise und praktischen Anwendung !
A = Amplitude
p = Periodenlänge
Δφ = sog. Offset, auch Phasenverschiebung ( math. „x- Verschiebung“ gg. das Vorzeichen!)
Der Tangens
…kann nicht einfach über den Einheitskreis definiert werden, weil dies der Abhängigkeit
Tan = Sin / Cos widerspricht !!! … man erhält ein falsches Vorzeichen !
Daher die abstrakte algebraische Definition: tan
(x ) = sin (x) / cos (x)
an den Stellen x = ungerades Vielfaches von π ist der Tangens nicht definiert: Werte ± ∞
Präge dir auch diese Kurve gut ein !
StD F.Sl 2010