Vorlesung 2

Nr.2- 21.04.2016
1
Logik in der Schule
Bildungsplan 2004 (Zitat:)
Begründen
Elementare Regeln und Gesetze der
Logik kennen und anwenden
Begründungstypen und Beweismethoden der Mathematik kennen,
gezielt auswählen und anwenden
2
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 1
Lernziel:
Der Sch. weiß,
dass ein mathematischer (Lehr-)Satz
die Form „Wenn [A], dann [B]“ hat.
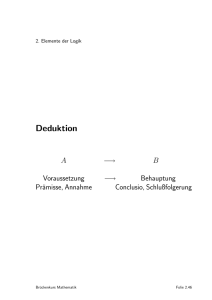
A: Voraussetzung
B: Behauptung
3
Die Form “Wenn [A], dann [B]“
erhellt die logische Struktur
Der Winkel im Halbkreis ist ein Rechter.
1. Wenn die Ecke C eines Dreiecks auf dem Halbkreis
über AB liegt, dann gilt
γ = 90°. Wahr
2. Wenn in einem Dreieck γ = 90° ist, dann liegt die
Ecke C auf dem Halbkreis über AB. wahr
4
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 2
Der Sch. soll „Für alle . . . “ - „Es gibt . . .“ – Aussagen
unterscheiden können bzw. aus dem Kontext
entnehmen, was gemeint ist.
Beispiel: Ist die Aussage wahr?
Wenn 2│n, dann 4│n
Schüler: Manchmal , kommt auf die Zahlen an.
Klarer ist:
1. Für alle nat. Zahlen gilt: Wenn 2│n, dann 4│n. Falsch
2. Es gibt eine nat. Zahl, so dass gilt: Wenn 2│n, dann
4│n. Wahr
5
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziele 3 und 4
Der Sch. soll zu einem Satz die Umkehrung bilden
können.
Satz:
Wenn x > 0, dann x^2 > 0. Wahr
Umkehrung: Wenn x^2 > 0, dann x > 0. Falsch
Satz:
Wenn x = 0, dann x^2 = 0. Wahr
Umkehrung: Wenn x^2 = 0, dann x = 0. Wahr
Der Sch. weiß, dass man von der Wahrheit eines Satzes
nicht auf die Wahrheit der Umkehrung schließen kann.
6
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 5
Der Sch. soll die logische Bedeutung von „notwendig“
und „hinreichend“ erläutern können.
Sei f beliebig oft differenzierbar.
Satz: Wenn f bei a eine Extremstelle hat, dann ist f´(a)=0.
wahr
f´(a)=0 ist notwendig für eine Extremstelle bei a. wahr
Eine Extremstelle bei a ist ausreichend für f´(a) = 0.
wahr!
7
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 6
Lernziel: Der Sch. soll wissen, dass
a) die Richtigkeit einer „es gibt Aussage“ mit der
Angabe eines Beispiels bewiesen ist.
b) die Falschheit einer „für alle Aussage“ mit der Angabe
eines Gegenbeispiels bewiesen ist.
8
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 6
Richtig oder falsch? Beweis mit Beispiel/Gegenbeispiel?
a) Es gibt eine Zahl n mit n^2 = 12n.
b) Jedes Viereck ist achsensymmetrisch oder
punktsymmetrisch.
c) Wenn n^2 gerade, dann n gerade.
9
Elementare Regeln und Gesetze der Logik
Didaktik: Lernziel 7
Lernziel:
Der Sch. soll wissen, dass
es Aussagen gibt, die man nicht durch ein Beispiel bzw.
ein Gegenbeispiel beweisen kann.
Wie dann?
→
Beweismethoden
10
Vorwissen zu Teilbarkeit
Definition für m teilt n, kurz m|n (m,n,k aus N\{0})
m|n genau dann, wenn ex. k mit m∙k = n.
Definition für gerade/ungerade Zahl
n gerade genau dann, wenn ex. k mit n = 2∙k
n ungerade genau dann, wenn ex. k mit n = 2∙k+1 (k≥0)
Begründungsbasis:
1. Rechnen in N, alle Rechenregeln
2. Eindeutige Primfaktorzerlegung
11
Der direkte Beweis
Satz: Wenn 6│n, dann 3│n.
Beweis:
6│n, also n = 6·k ; Defini\on „teilt“
also n = 2·3·k ; elementares Rechnen
also n = 3·(2·k); Rechenregeln
also n = 3·j mit j=2k
also 3│n
; Definition „teilt“
Die Umkehrung ist falsch.
12
Der direkte Beweis
Aussagenlogische Analyse
[A ᴧ (A→B)] → B ist Tautologie.
Weiter: [B ᴧ (B→C)] → C [C ᴧ (C→D)] → D usw.
13
Die Kontraposition
Alltagslogik: Das sind äquivalente Aussagen
Wenn Fred am 11.11. in Stuttgart einen Mord verübt
hat, dann war er am 11.11. in Stuttgart.
Wenn Fred am 11.11. nicht in Stuttgart war, dann hat
er am 11.11. in Stuttgart keinen Mord verübt.
14
Die Kontraposition
Aussagenlogische Analyse
Beweis: A ⇒ B ist äquivalent ¬B ⇒ ¬ A
15
Die Kontraposition
1. A→B und ¬B→¬ A sind logisch äquivalent
2. ¬B→¬ A heißt Kontraposi\on zu A→B
3. Staa A→B zu beweisen ist es gleichwer\g
¬B→¬ A zu beweisen.
Beachte: Umkehrung von A→B ist B→A.
Das ist nicht die Kontraposition
16
Die Kontraposition
Zeige: Wenn n² gerade, dann n gerade.
Beweis mit Kontraposition.
Zu zeigen: Wenn n ungerade, dann n² ungerade.
n ungerade, also n = 2∙k+1
; Def. ungerade
also n² = 4k²+4k+1
; Algebra
also n² = 2(2k²+2k)+1 ; Algebra
also n² = 2∙j+1 mit j=2k²+2k
also n² ungerade
17
Beweis durch Widerspruch
(Kontradiktion)
Ein historisches Beispiel in der Vorlesung
Aussagenlogische Form dieses Beweisschemas:
[ A→(Bᴧ¬B)] → ¬A
Beweis mit Wahrheitstafel:
Zeige [ A→(Bᴧ¬B)] → ¬A ist Tautologie.
18
Beispiel: Beweis durch Widerspruch
Zeige A: √2 kann man nicht als Bruch a/b schreiben
(a,b aus Z)
Beweis mit Widerspruch:
Annahme:
√2 = a/b
dann
2 = a²/b²
dann 2b² = a²
Wie geht der Beweis weiter?
19
Beweisen in der Schule
Didaktische Fragen:
Soll man immer beweisen?
Welche Gründe würden dagegen sprechen?
Welches sind die Beweismittel (Begründungsbasis)?
Reicht ein exemplarischer Beweis?
Usw.