Transferbeispiel 5-4 „Empirische Elastizitäten“

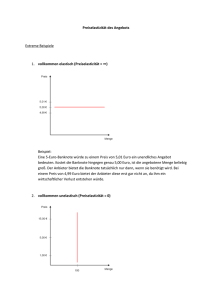
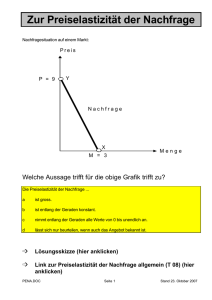
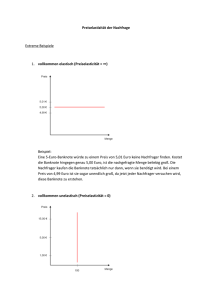
Prof. Dr. H.-D. Hardes
FB IV – VWL/APO
WS 2002/03
Grundzüge der Volkswirtschaftslehre
Transferbeispiel 5-4
„Empirische Elastizitäten“
Schätzung von Nachfragekurven mit konstanter Preiselastizität
Eine häufig verwendete Funktionsgleichung einer Nachfragekurve mit konstanter Preiselastizität lautet:
x = a · pε
Hier bezeichnet x die nachgefragte Menge, p den Preis; a und ε sind konstante Parameter. Es
kann gezeigt werden, dass der Exponent ε des Preises in dieser Funktion die Preiselastizität
der Nachfrage misst.
Standardmethoden der Statistik zur Anpassung von Kurven an empirische Daten erfordern,
dass die geschätzten Kurven selbst linear sind. Das ist im Fall einer Nachfragekurve mit
konstanter Preiselastizität problematisch, da diese Kurven konvex zum Ursprungspunkt
verlaufen. Die Lösung dieses Problems liegt darin, dass die Ursprungsfunktion log-linear ist.
Eine einfache lineare Funktion kann ermittelt werden, indem man die Funktion in eine loglineare Funktion mit natürlichen Logarithmus-Größen transformiert:
ln(x) = ln(a) + ε · ln(p)
Angenommen sei, die beobachteten Kaufmengen eines Gutes entsprechen der effektiven
Marktnachfrage. Dann kann eine Nachfragekurve mit konstanter Preiselastizität einfach
geschätzt werden, indem man die zu verschiedenen Zeitpunkten beobachteten Preise und
zugehörigen Mengen logarithmiert und eine lineare Kurve an die transformierten Daten
anpasst (Abb. 4-18). Der Schnittpunkt der geschätzten Gerade mit der Ordinate ergibt in
delogarithmierter Form den Lageparameter a; das Steigungsmaß der geschätzten Gerade
entspricht dem Wert der Preiselastizität. ...
(Empirische Preis- und Einkommenselastizitäten lassen sich berechnen, wenn man die obige
Nachfragefunktion mit konstanter Preiselastizität durch eine weitere Variable, die Pro-KopfEinkommen der Haushalte, erweitert.) Die preisbereinigten Ausgaben für eine bestimmte
Gütergruppe werden in Abhängigkeit zweier unabhängiger Variablen, der Entwicklung der
Pro-Kopf-Einkommen aller Haushalte (YPOP) und der spezifischen Preisentwicklung (pi) der
Gütergruppe, betrachtet.
xi = a ⋅ YPOPb + pic
Durch log-lineare Transformation erhält man den Typ einer Regressionsfunktion mit
transformierten Variablen, deren Parameter als Schätzwerte der empirischen Einkommens(εY) und Preiselastizitäten (ε) der Gütergruppe zu interpretieren sind.
2
ln(xi) = ln(a) + b ⋅ ln(YPOP) + c ⋅ ln(pi)
↓
εY
↓
ε
Die Schätzungen der empirischen Einkommens- und Preiselastizitäten erfordern für jeweilige
Gütergruppen drei Datenreihen eines Untersuchungszeitraums, die Entwicklung
− preisbereinigter Ausgaben der Haushalte (xi),
− der Pro-Kopf-Einkommen (YPOP) und
− der Güterpreise (pi).
Abb. 4-18: Schätzung einer Nachfragekurve mit konstanter Preiselastizität
p
(a) Nachfragekurve
ln (p)
(b) Transformierte Nachfragekurve
1000
800
600
7
6
5
400
4
200
3
D‘
D
200
400
600
800
1000 x
3
4
5
6
7
ln (x)
Lageparameter und Preiselastizität einer Nachfragekurve mit konstanter Preiselastizität
können statistisch ermittelt werden, indem man die Daten der Ausgangskurve durch eine
log-lineare Transformation ersetzt.
Quelle: Hardes/Schmitz/Uhly, Grundzüge der VWL, 8.Aufl., München,Wien 2002, S.158 ff.
Aufgaben/Fragen zu Transferbeispiel 5-4
(1)
Reflektieren Sie die Vorgehensweise zur Ermittlung empirischer Preis- bzw.
Einkommenselastizitäten! Angenommen, Sie stehen vor der Aufgabe, empirische
Elastizitäten für bestimmte Gütergruppen zu schätzen, wie würden Sie hierzu
verfahren?
Transferbeispiel 5-5 WS 02-03.doc