Wärmelehre

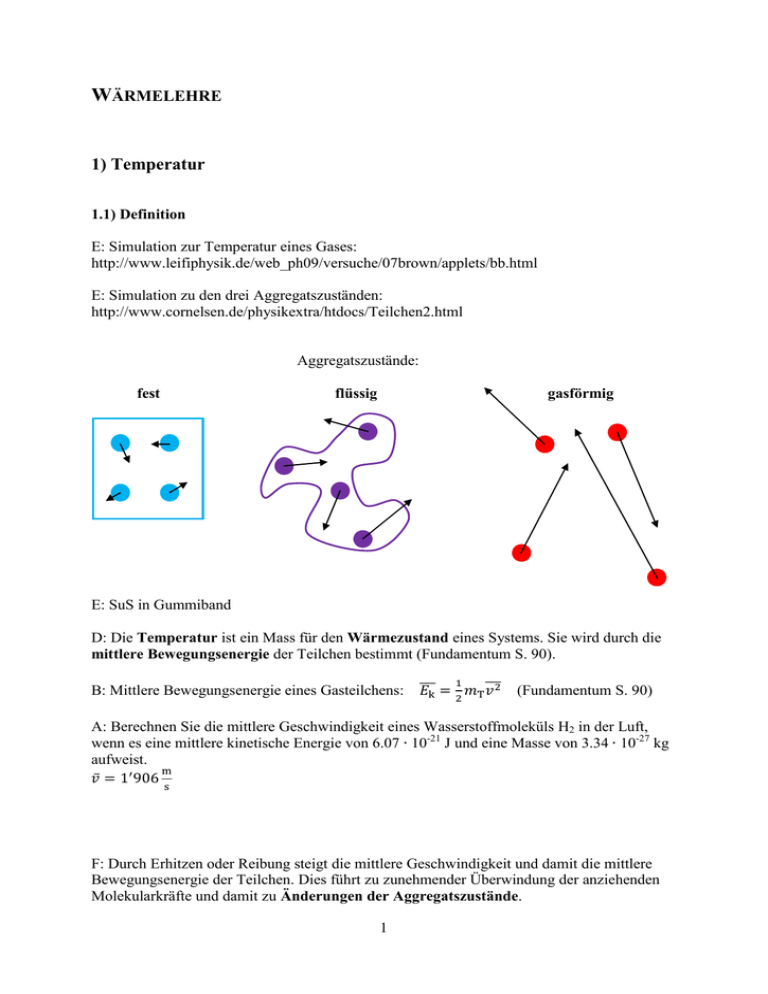
WÄRMELEHRE
1) Temperatur
1.1) Definition
E: Simulation zur Temperatur eines Gases:
http://www.leifiphysik.de/web_ph09/versuche/07brown/applets/bb.html
E: Simulation zu den drei Aggregatszuständen:
http://www.cornelsen.de/physikextra/htdocs/Teilchen2.html
Aggregatszustände:
fest
flüssig
gasförmig
E: SuS in Gummiband
D: Die Temperatur ist ein Mass für den Wärmezustand eines Systems. Sie wird durch die
mittlere Bewegungsenergie der Teilchen bestimmt (Fundamentum S. 90).
B: Mittlere Bewegungsenergie eines Gasteilchens:
(Fundamentum S. 90)
A: Berechnen Sie die mittlere Geschwindigkeit eines Wasserstoffmoleküls H2 in der Luft,
wenn es eine mittlere kinetische Energie von 6.07 10-21 J und eine Masse von 3.34 10-27 kg
aufweist.
F: Durch Erhitzen oder Reibung steigt die mittlere Geschwindigkeit und damit die mittlere
Bewegungsenergie der Teilchen. Dies führt zu zunehmender Überwindung der anziehenden
Molekularkräfte und damit zu Änderungen der Aggregatszustände.
1
1.2) Temperaturskalen
D: Die Celsius-Temperatur  bezieht sich auf das Schmelzen (0 °C) und Verdampfen
(100 °C) von Wasser, wobei gilt: [] = °C = Grad Celsius
D: Die Absolute Temperatur T hat ihren Nullpunkt bei ‒273.15 °C,
wobei gilt: [T] = K = Kelvin
, [] = °C
‒273.15
0
100
200
T, [T] = K
0
273.15
373.15
473.15
A: Rechnen Sie 50 °C in K und 50 K in °C um.
323.15 K, ‒223.15 °C
F: Für eine Temperaturdifferenz gilt:
A: Was bedeutet 0 K für die Teilchenbewegung?
S: Der Zusammenhang zwischen der mittleren Geschwindigkeit und der Temperatur eines
Gasteilchens ist:
, mit k = 1.38 10-23 (Boltzmann-Konstante, Fund. S. 90)
A: Berechnen Sie die Temperatur des H2-Moleküls aus vorigem Kapitel.
T = 293.24 K ( = 20.09 °C)
2) Wärmeausdehnung
2.1) Längenänderung
E: Eisenkugel erhitzen
E: Stab erhitzen
l
l
2
A: Wovon hängt die Längenänderung
S:
ab?
(Fundamentum S. 90 und 102)
D: Der Längenausdehnungskoeffizient gibt an, um wie viel sich die Länge eines
bestimmten Körpers bei Temperaturschwankung verändert, wobei gilt:
A: Die Kirchenfeldbrücke (Stahl) ist im Winter (‒5 °C) 230 m lang. Wie lang wäre sie im
Sommer (35 °C)?
= 0.15 m, Sommer = 230.15 m
2.2) Volumenänderung
E: Wasserkugel erhitzen
S:
(Fundamentum S. 90 und 102)
D: Der Volumenausdehnungskoeffizient gibt an, um wie viel sich das Volumen
bestimmten Körpers bei Temperaturschwankung verändert, wobei gilt:
eines
A: Um wie viel dehnt sich ein Liter Wasser aus, wenn Sie ihn aus dem Kühlschrank (5°C)
genommen und an die Sonne gegeben haben (40°C)?
= 7.35 10-3 dm3 (7.35 10-6 m3)
E: „Luftkugel“ erhitzen
S: Alle Körper vergrössern mit steigender Temperatur ihr Volumen bei gleich bleibender
Masse, d.h., ihre Dichte verringert sich (Ausnahmen: Gummi, Wasser).
A: Bei welcher Temperatur hat Wasser seine grösste Dichte ( → „Dichteanomalie“)?
3
3) Wärme Q
3.1) Definition
D: Die Wärme Q ist eine Energieübertragungsgrösse. (Fundamentum S. 91)
3.2) Spezifische Wärmekapazität cp
E: Wasser mit Tauchsieder erhitzen. Dabei wird Wärme vom Sieder auf das Wasser
übertragen. Zeit t bis zum Kochen messen.
m
T
m
T+T
Q
Leistung des Tauchsieders: P = 1‘000 W
Masse des Wassers: m = 0.3 kg
Temperaturdifferenz: T = 80 K (100°C ‒ 20°C)
Gemessene Zeitdauer: t =
A: Wovon hängt die auf das Wasser übertragene Wärme Q ab?
-
je grösser Q, desto grösser T (bei gleichem m).
je grösser Q, desto grösser darf m sein (bei gleichem T)
ausserdem: materialabhängig
S: Q = cp ∙ m ∙ T (Fundamentum S. 91)
D: Die spezifische Wärmekapazität cp gibt diejenige Energiemenge an, die einem Körper
von 1 kg Masse zugeführt werden muss, um dessen Temperatur um 1 K zu erhöhen.
A: Berechnen Sie für obiges Experiment cp von flüssigem Wasser.
A: Was bedeutet es für das Aufheizen und Abkühlen, wenn ein Körper eine grosse spezifische
Wärmekapazität hat?
A: Was unterscheidet Maritim- von Kontinentalklima?
4
A: In einer Badewanne befinden sich 80 l Wasser von 90 °C. Wie viel Wasser von 20 °C
muss man dazu mischen, so dass das Bad schliesslich eine Temperatur von 37 °C aufweist?
m1 = 249 kg
3.3) Änderung der Aggregatszustände
B: Wasser
sublimieren
verdampfen
schmelzen
fest
flüssig
0 °C
erstarren
100 °C
kondensieren
gasförmig
resublimieren
3.3.1) Schmelzen und Erstarren
D: Die Schmelztemperatur f ist diejenige Temperatur, bei der sich die kristalline Struktur
eines Festkörpers auflöst.
D: Die spezifische Schmelzwärme Lf ist diejenige Energiemenge, die einem Körper von 1 kg
Masse zugeführt werden muss, um diesen zu schmelzen.
S: Q = Lf ∙ m
A: Welche Wärmemenge ist nötig, um 800 kg Eisen zu schmelzen?
Q = 2.216 ∙ 108 J (222 MJ)
A: Wie obige Aufgabe, aber mit Ausgangstemperatur von 20°C
Qtotal = Qerwärmen + Qschmelzen = 767 MJ
5
D: Die Erstarrungstemperatur ist diejenige Temperatur, bei der sich die kristalline Struktur
eines Festkörpers bildet. Sie ist gleich hoch wie die Schmelztemperatur.
D: Die spezifische Erstarrungswärme ist diejenige Energiemenge, die einem Körper der
Masse 1 kg entzogen werden muss, um diesen erstarren zu lassen. Sie ist gleich gross wie die
spezifische Schmelzwärme.
S: Erstarrt ein Körper, wird Energie frei!
E: Wärmebeutel
E: Eis-Wasser-Gemisch erhitzen, Temperatur ständig messen
S: Weder beim Schmelzen noch beim Erstarren ändert sich die Temperatur eines Körpers.
3.3.2) Verdampfen und Kondensieren
D: Die Siedetemperatur V ist diejenige Temperatur, bei der eine Flüssigkeit gasförmig
wird.
D: Die spezifische Verdampfungswärme LV ist diejenige Energiemenge, die einem Körper
von 1 kg Masse zugeführt werden muss, um diesen zu verdampfen.
S: Q = LV ∙ m
(Fundamentum S. 91 und 102)
A: Welche Wärmemenge ist nötig, um 0.8 kg Wassereis von -10°C vollständig in
Wasserdampf umzuwandeln?
Qtotal = 2.42 MJ
D: Die Kondensationstemperatur ist diejenige Temperatur, bei der sich Gas in Flüssigkeit
verwandelt. Sie ist gleich hoch wie die Siedetemperatur.
D: Die spezifische Kondensationswärme ist diejenige Energiemenge, die einem Körper der
Masse 1 kg entzogen werden muss, um diesen zu verflüssigen. Sie ist gleich gross wie die
spezifische Verdampfungswärme.
S: Kondensiert ein Gas, wird Energie frei!
B: Quellwolken (http://www.youtube.com/watch?v=ll3i35UrNEw&feature=related)
E: Wasser sieden, Temperatur ständig messen
S: Weder beim Verdampfen noch beim Kondensieren ändert sich die Temperatur eines
Körpers.
6
3.3.3) Verdunsten
A: Wie sieht die Häufigkeitsverteilung der Geschwindigkeiten der Wassermoleküle in einer
Pfütze von 20 °C aus?
Anzahl Moleküle n
Molekülgeschwindigkeit v, [v] =
F: Die Häufigkeiten der Geschwindigkeiten folgen einer so genannten Maxwell-Verteilung,
deren Maximum der mittleren Geschwindigkeit aller Moleküle (s. Seite 1) und damit der
Temperatur der Pfütze entspricht.
A: Weshalb kann sich diese Wasserpfütze auch bei 20°C allmählich in Wasserdampf
umwandeln?
F: Auch bei 20°C gibt es Moleküle, deren Geschwindigkeit einer Temperatur über 100 °C
entspricht. Diese können die Flüssigkeit verlassen und kehren nicht mehr zurück.
A: Was passiert mit der Temperatur der verbleibenden Flüssigkeit?
F: Verliert die Pfütze ständig seine schnellsten Teilchen, sinkt die mittlere Geschwindigkeit
und damit die Temperatur → „Verdunstungskälte“
7
A: Weshalb haben Sie kalt, wenn Sie im Sommer aus der Aare steigen, obwohl die
Lufttemperatur 35°C beträgt?
E: Alkohol auf Haut
A: Wie lange dauert dieser Kühlungsprozess?
A: Was begünstigt den Verdunstungsprozess?
B für Verdunstungskälte: Schwitzen (Abbildung 1)
Abbildung 1
Abbildung 2
3.3.4) Sublimieren und Resublimieren
A: Was ist Trockeneis und woher hat es seinen Namen?
E: Trockeneis (Abbildung 2)
A: Weshalb muss man den Kühlschrank ab und zu enteisen?
B für Resublimation: Eisblumen an schlecht isolierten Fenstern (Abbildung 3)
Abbildung 3
Abbildung 4
8
3.4) Luftfeuchtigkeit
A: Wo ist das flüssige Wasser nach dem Verdunsten bzw. Verdampfen?
F: Beim Verdunsten oder Verdampfen nimmt die Luft das Wasser auf. Dabei ändern die H2OMoleküle ihren chemischen Aufbau nicht.
D: Die Luftfeuchtigkeit gibt den gasförmigen Wassergehalt der Luft an
(Fundamentum S. 91).
D: Die absolute Luftfeuchtigkeit a gibt an, wie viele Gramm Wasser in einem Kubikmeter
Luft enthalten ist.
F: a =
; [a] =
wobei: V = Volumen der Luft
A: In der Luft des Schulzimmers (4 m × 8 m × 12 m) sind 4 Liter Wasser enthalten.
Berechnen Sie die absolute Luftfeuchtigkeit.
a = 10.4
A: Warum ist es in der Sauna dunstig (Abbildung 4, S. 8)?
D: Die Sättigungsdampfdichte s gibt an, wie viele Gramm Wasser ein Kubikmeter Luft
maximal aufnehmen kann.
F: Wird die Sättigungsdampfdichte überschritten, kondensiert das Wasser wieder aus
(Wolken, Nebel, Tau).
A: Wovon hängt die Sättigungsdampfdichte ab (Fundamentum S. 103)?
A: Wie viel Wasser könnte unser Schulzimmer bei 20 °C maximal aufnehmen?
m = 6‘651 g (6.7 Liter)
D: Die relative Luftfeuchtigkeit r gibt an, zu wie viel Prozent die Luft mit Wasser
gesättigt ist.
S:
A: Berechnen Sie die relative Luftfeuchtigkeit in unserem Schulzimmer ( = 20 °C).
r = 60 %
A: Was passiert mit der absoluten und was mit der relativen Luftfeuchtigkeit, wenn die Luft
im Schulzimmer aufgeheizt bzw. abgekühlt wird?
F: Ist in der Luft die Sättigungsdampfdichte erreicht, herrscht 100 % rel. Luftfeuchtigkeit.
9
4) Wärmetransport
F: Wärme kann auf drei verschiedene Arten von einem Körper auf einen anderen übertragen
werden:
4.1) Wärmeleitung
E: Verschiedene gleichlange Stäbe erhitzen
F: Wärme wandert von selbst durch ein Material (Nachbarmoleküle werden angestossen).
Q
S: Bei der Wärmeleitung wird die Energie ohne Materietransport weitergeleitet.
E: Eis schmilzt in kochendem Wasser nicht sofort.
E: Wassertropfen verdampfen nicht sofort sondern „schweben“ auf der heissen Herdplatte, da
der Wasserdampf eine isolierende Schicht bildet (Leidenfrostsches Phänomen):
flüssiges
S: Metalle sind gute, Flüssigkeiten und Gase schlechte Wärmeleiter.
10
A: Weshalb isolieren Eisbärfell (links) und Styropor (rechts) gut?
D: Die Wärmeleitfähigkeit  gibt an, wie gut ein Material die Wärme leitet.
(Fundamentum S. 102)
S: Die pro Zeit t durch ein Material der Querschnittsfläche A, der Schichtdicke x und der
Wärmeleitfähigkeit  geleitete Wärmemenge Q ist (Fundamentum S. 91):
T2 < T1
T1






A
x
A: Der Boden einer runden Aluminiumpfanne (Durchmesser 20 cm) ist 6 mm dick. Die 20 °C
warme Pfanne wird auf eine 80 °C heisse Herdplatte gestellt. Wie viel Wärme wird pro
Sekunde ins Pfanneninnere geleitet?
Q = 75 kJ
4.2) Konvektion
E: Handpropeller, Kerzenkarussell
F: Warme aufsteigende Luft treibt
Propeller an.
11
E: Wasserzirkulation im Rechteckrohr
B: „kochende“ Sonnenoberfläche (http://www.uni-sw.gwdg.de/~bruno/APOD/apod.html)
S: Im Gegensatz zur Wärmeleitung strömt bei der Konvektion die Energie mit der Materie
mit.
A: Weshalb hat es Rippen an Motorzylindern und weshalb hat man doppel- oder gar
dreifachverglaste Fenster?
4.3) Wärmestrahlung
B: Von der Sonne wird Energie durch das Vakuum hindurch zur Erde abgestrahlt.
E: 2 Aluspiegel mit einer Wärmequelle im einen Brennpunkt
Vakuum
S: Wärmestrahlung ist Energietransport ohne Materie.
12
D: Die Emissionszahl  gibt an, wie stark die Oberfläche eines Materials Wärme abstrahlt.
S: Die von einem strahlenden Körper mit Oberfläche A und Emissionszahl pro Zeiteinheit
t abgegebene Wärmemenge Q ist (Fundamentum S. 91 und 103):


A: Wie viel Energie strahlt ein Mensch (A = 2 m2,  = 30 °C) in einer Sekunde ab?
Q = 938.58 J
A: Wie wird bei einer Thermosflasche der Wärmeverlust verhindert?
A: Weshalb streuen Bauern im Frühling schwarze Asche auf den weissen Schnee?
F: Körper mit schwarzer Oberfläche können mehr Energie aufnehmen (absorbieren) als
Körper mit weisser Oberfläche. Sie strahlen aber auch stärker ab.
A: Wie kommt es zum Treibhauseffekt?




Sichtbares Licht von der Sonne hat sein Strahlungsmaximum bei Gelb (600 nm
Wellenlänge).
Es wird weniger durch die Erdatmosphäre und mehr durch die Erdoberfläche
absorbiert.
Die Wärmeabstrahlung der nunmehr aufgeheizten Erdoberfläche hat ihr Maximum im
Infrarot-Bereich (800 nm Wellenlänge).
Und diese Strahlung wird von der Erdatmosphäre stark absorbiert → Aufheizen der
Atmosphäre (beschleunigt durch diverse Gase).
13
5.) Hauptsätze der Wärmelehre
5.1) Innere Energie U
F: Moleküle können noch andere Bewegungen als reine Verschiebungen vollführen
(Schwingungen, Rotationen, …).
B: Schwingungen eines dreiatomigen linearen Moleküls
D: Die innere Energie U ist die gesamte kinetische Energie der sich bewegenden Teilchen in
einem Körper.
F: Je grösser die innere Energie eines Körpers desto grösser ist auch seine Temperatur.
F: Der Energieerhaltungssatz aus der Mechanik (s. „Mechanik“, Kap. 4.4) muss somit
ergänzt werden.
S:
F: Umwandlungen von einer Energieform in eine andere sind auch hier möglich.
B: Dampfmaschine wandelt innere Energie in kinetische Energie um.
14
5.2) Erster Hauptsatz der Wärmelehre
A: Wie kann die innere Energie U eines Körpers erhöht werden?
E: Metall durch Flamme oder „Schmieden“ aufheizen
U
U + U
U
U + U
F: Die innere Energie U kann durch Zuführen von Wärme und/oder Arbeit erhöht werden.
1. Hauptsatz: Fügen wir einem Körper die Wärmemenge Q und die Arbeit W zu, so erhöht
sich seine innere Energie U um U.
S: 
(Fundamentum S. 92)
F: Es gibt alternative Formulierungen des 1. Hauptsatzes:



In einem energetisch abgeschlossenen System bleibt die Gesamtenergie konstant.
Energie kann nicht erzeugt, sondern nur umgewandelt und übertragen werden.
Es gibt kein Perpetuum Mobile 1. Art.
D: Ein Perpetuum Mobile 1. Art ist eine Maschine, die ohne Antrieb ständig läuft.
B: Dampfmaschine, die Arbeit verrichtet ohne aufgeheizt zu werden.
B für Perpetua Mobilia aus der Mechanik und Hydrodynamik
15
5.3) Zweiter Hauptsatz der Wärmelehre
E: Zwei identische Metallklötze von unterschiedlichen Temperaturen werden
zusammengefügt.
m1 = 1 kg
1 = 80 °C
m2 = 1 kg
2 = 20 °C
Q
m3 =
3=
A: Was passiert?
F: Der wärmere Klotz wird solange Wärme an den kälteren Klotz abgeben, bis beide die
gleiche Temperatur haben.
2. Hauptsatz: Wärme strömt immer selbständig von Orten höherer Temperatur zu Orten mit
niedrigerer Temperatur, nie umgekehrt (Fundamentum S. 92).
F: Auch hier gibt es alternative Formulierungen:


Abgeschlossene Systeme streben einen Zustand maximaler Unordnung bzw. grösster
Wahrscheinlichkeit an (Prinzip der maximalen Entropie).
Es gibt kein Perpetuum Mobile 2. Art.
D: Ein Perpetuum Mobile 2. Art ist eine Maschine, die Wärme vollständig in Arbeit
umwandeln kann.
B: Dampfmaschine, die ohne Wärmeverlust 100% der Wärme in Arbeit verwandeln kann.
F: Bei jeder Maschine, die Energien umwandelt, gibt es „Energieverluste“ (Abwärme,
Reibungsverluste, etc.).
B: Benzinmotor wandelt chemisch gespeicherte Energie in mechanische Energie um. Dabei
werden der Motor, die Kühlflüssigkeit, die Lager, die Auspuffgase, die Räder etc. aufgeheizt.
16
6) Wirkungsgrade
6.1) Wärmekraftmaschinen WKM
A: Was passiert, wenn die Luft in einer verschlossenen Spritze aufgeheizt wird?
F: Das Gas verrichtet Arbeit wegen der Wärmeausdehnung.
A: Was ist nötig, um daraus eine zyklisch arbeitende Maschine bauen zu können?
A: Erklären Sie das Prinzip einer Dampfmaschine nach James Watt.
Dampfkessel
Pumpkolben
Kondensator
Einlassventil
Auslassventil
Arbeitszylinder
17
F: Eine Wärmekraftmaschine (WKM) entzieht einem heissen Energiereservoir Wärme,
welche sie in Arbeit umwandelt. Dies gelingt aber gemäss 2. Hauptsatz der Wärmelehre nicht
zu 100%, denn es wird ein Teil der entzogenen Wärme an ein kaltes Energiereservoir
abgegeben.
A: WKM-Schema gemäss Fundamentum S. 92. Wo ist was bei der Dampfmaschine?
TW:
QW:
WKM:
TK:
QK:
WN:
D: Der reale Wirkungsgrad real (Wirkungsgrad einer real existierenden Maschine) ist das
Verhältnis von Nutzarbeit WN zu Antriebswärme QW (Fundamentum S. 92):
S:
A: Eine Dampfmaschine leistet 4.5 kJ Arbeit aus einer Wärmemenge von 22kJ. Berechnen
Sie den realen Wirkungsgrad.
real = 0.20 (oder 20%)
A: Wie gross wäre der reale Wirkungsgrad, wenn die Maschine entweder keine Nutzarbeit
leistet oder sämtliche Antriebswärme in Nutzarbeit umwandeln könnte?
real = 0 bzw. 1
A: Ist bei einer realen Maschine ein Wirkungsrad von 1 überhaupt möglich?
F: Gemäss 2. Hauptsatz der Wärmelehre gibt es immer Abwärme QK (Fundamentum S. 92)
D: Der theoretische Wirkungsgrad Carnot (maximaler theoretischer Wirkungsgrad einer
idealen Maschine) ist das Verhältnis aus der Temperaturdifferenz von Antriebswärme zu
Abwärme (TW – TK) und der Temperatur der Antriebswärme:
S:
A: Der Dampf einer Dampfmaschine habe eine Temperatur von 250 °C, die an die Umwelt
abgegebene Abluft eine Temperatur von 50 °C. Berechnen Sie den theoretischen
Wirkungsgrad.
Carnot = 0.38 (oder 38%)
18
A: In welcher Situation ist der theoretische Wirkungsgrad 0 bzw. 1?
F: Je grösser die Temperaturdifferenz zwischen den beiden Wärmereservoirs, desto grösser ist
der theoretische Wirkungsgrad.
A: Wie funktionieren Verbrennungsmotoren?
E: Neufelder Tischbombe
F: Durch Verbrennung von Benzin-Luftgemisch erzeugte Wärme lässt Luft
schlagartig expandieren.
A: Erklären Sie das Prinzip eines Vier- und des Zweitaktmotors
(http://upload.wikimedia.org/wikipedia/commons/a/a6/4-Stroke-Engine.gif,
http://upload.wikimedia.org/wikipedia/commons/3/33/Two-Stroke_Engine.gif).
19
6.2) Wärmepumpe WP
F: Eine WKM entnimmt einem heisseren Wärmereservoir Arbeitswärme und überträgt die
Abwärme in ein kälteres Wärmereservoir. Dabei wird Nutzarbeit geleistet.
A: Was muss geschehen, wenn eine Maschine dem kälteren Reservoir Wärme entziehen und
in ein heisseres Reservoir abgeben will (obwohl dies auf den ersten Blick nicht sehr sinnvoll
erscheint)?
F: Eine Wärmepumpe kehrt die Energieflüsse um („rückwärts“ laufende WKM)
B: Kühlschrank
A: WP-Schema gemäss Fundamentum S. 92. Wo ist was beim Kühlschrank?
TW:
QW:
WP:
TK:
QK:
WA:
F: Die Nutzarbeit WN wurde zur Antriebsarbeit WA, die Antriebswärme QW zur Heizwärme
QW und die Abwärme QK zur Umweltwärme QK.
20
A: Was passiert mit dem realen Wirkungsgrad einer WP (Fundamentum S. 92)?
S:
A: Eine Wärmepumpe führt der Zimmerluft eine Wärmemenge von 2 MJ unter einem
Arbeitsaufwand von 560 kJ zu. Berechnen Sie den realen Wirkungsgrad.
real = 3.57 (oder 357 %)
A: In welcher Situation ist der reale Wirkungsgrad minimal?
A: Wann wird er grösser?
F: Der reale Wirkungsgrad ist eine Zahl, die grösser als 1 ist.
A: Was passiert mit dem theoretischen Wirkungsgrad?
S:
A: Ein Kühlschrank weist im Gefrierfach eine Temperatur von -15 °C auf. Die Küchenluft
betrage 22 °C. Berechnen Sie den theoretischen Wirkungsgrad.
Carnot = 7.98 (oder 798 %)
A: Was passiert, wenn das kältere Wärmereservoir eine Temperatur von 0K hätte?
F: Je grösser die Temperaturdifferenz zwischen den beiden Wärmereservoirs, desto kleiner ist
der theoretische Wirkungsgrad.
F: Nicht nur die Energieflüsse sondern auch die Wirkungsgrade werden invertiert.
21