Gleichmäßig beschleunigte Bewegung und Beschleunigung

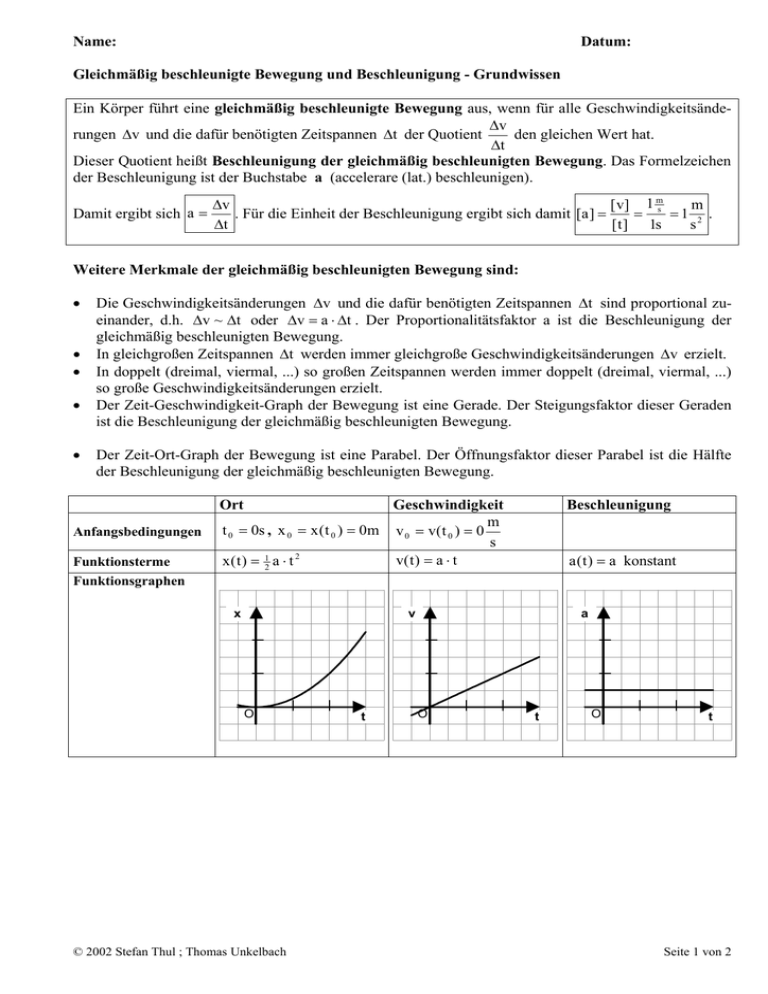
Name:
Datum:
Gleichmäßig beschleunigte Bewegung und Beschleunigung - Grundwissen
Ein Körper führt eine gleichmäßig beschleunigte Bewegung aus, wenn für alle Geschwindigkeitsände∆v
rungen ∆v und die dafür benötigten Zeitspannen ∆t der Quotient
den gleichen Wert hat.
∆t
Dieser Quotient heißt Beschleunigung der gleichmäßig beschleunigten Bewegung. Das Formelzeichen
der Beschleunigung ist der Buchstabe a (accelerare (lat.) beschleunigen).
Damit ergibt sich a =
∆v
[ v] 1 ms
m
=
=1 2 .
. Für die Einheit der Beschleunigung ergibt sich damit [a ] =
∆t
[ t ] 1s
s
Weitere Merkmale der gleichmäßig beschleunigten Bewegung sind:
•
•
•
•
•
Die Geschwindigkeitsänderungen ∆v und die dafür benötigten Zeitspannen ∆t sind proportional zueinander, d.h. ∆v ~ ∆t oder ∆v = a ⋅ ∆t . Der Proportionalitätsfaktor a ist die Beschleunigung der
gleichmäßig beschleunigten Bewegung.
In gleichgroßen Zeitspannen ∆t werden immer gleichgroße Geschwindigkeitsänderungen ∆v erzielt.
In doppelt (dreimal, viermal, ...) so großen Zeitspannen werden immer doppelt (dreimal, viermal, ...)
so große Geschwindigkeitsänderungen erzielt.
Der Zeit-Geschwindigkeit-Graph der Bewegung ist eine Gerade. Der Steigungsfaktor dieser Geraden
ist die Beschleunigung der gleichmäßig beschleunigten Bewegung.
Der Zeit-Ort-Graph der Bewegung ist eine Parabel. Der Öffnungsfaktor dieser Parabel ist die Hälfte
der Beschleunigung der gleichmäßig beschleunigten Bewegung.
Ort
Anfangsbedingungen
Funktionsterme
Funktionsgraphen
Geschwindigkeit
m
t 0 = 0s , x 0 = x ( t 0 ) = 0m v 0 = v( t 0 ) = 0
s
2
1
v( t ) = a ⋅ t
x(t) = 2 a ⋅ t
x
Beschleunigung
a ( t ) = a konstant
v
O
© 2002 Stefan Thul ; Thomas Unkelbach
t
a
O
t
O
t
Seite 1 von 2
Anfangsbedingungen
Funktionsterme
Funktionsgraphen
Ort
Geschwindigkeit
t 0 = 0s , x 0 = x ( t 0 ) = 0m v 0 = v( t 0 ) ≠ 0m / s
v( t ) = a ⋅ t + v 0
x ( t ) = 12 a ⋅ t 2 + v 0 ⋅ t
x
t 0 = 0s , x 0 = x ( t 0 ) ≠ 0m
x ( t ) = 12 a ⋅ t 2 + x 0
x
Funktionsterme
Funktionsgraphen
Geschwindigkeit
m
v 0 = v( t 0 ) = 0
s
v( t ) = a ⋅ t
Beschleunigung
a ( t ) = a konstant
x
© 2002 Stefan Thul ; Thomas Unkelbach
t
t
Beschleunigung
v( t ) = a ⋅ t + v 0
a ( t ) = a konstant
v
O
O
t
Ort
Geschwindigkeit
t 0 = 0s , x 0 = x ( t 0 ) ≠ 0m v 0 = v( t 0 ) ≠ 0m / s
x ( t ) = 12 a ⋅ t 2 + v 0 ⋅ t + x 0
t
a
O
t
O
t
v
O
Anfangsbedingungen
a
O
t
Ort
Funktionsterme
Funktionsgraphen
a ( t ) = a konstant
v
O
Anfangsbedingungen
Beschleunigung
a
O
t
O
t
Seite 2 von 2