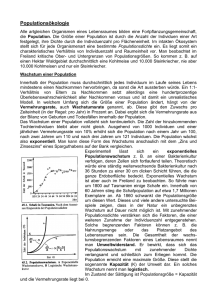
68-95-99

Biostatistik
5. Normalverteilung.
Standardfehler.
Konfidenzintervalle.
Die Normalverteilung N(, 2)




Die Normalverteilung ist die wichtigste
Verteilung in Statistik.
Sie hat zwei Parameter:
 = Erwartungswert oder Mittelwert, und
2 = Varianz ― oder:
 = Standardabweichung der Verteilung.
Die Notation X ~ N(, 2) bedeutet, daß die
Zufallsvariable X normalverteilt ist mit den
Parametern  (Mittelwert) und 2 (Varianz).
Die Normalverteilung N(0, 1) heißt
Standardnormalverteilung
(ihre Parameter sind: =0 und 2 =1)
Biostatistik-5
2
Normalverteilung N(, 2)

Verteilungsfunktion F(x) und Dichtefunktion f(x) für
X ~ N(,
 2)
:
x
F ( x )  P( X  x ) 
 f (t ) d t ,



wo
1
f ( x) 
e
2 

( x   )2
2 2
Die Dichtefunktion der Normalverteilung ist eine symmetrische (auf
), eingipflige Glockenkurve, oft Gaußsche Kurve genannt.  ist
nicht nur Mittelwert, sondern auch Median und Modalwert der
Verteilung.
 bestimmt die Lage (Position) der Kurve f(x)
2 (oder ) bestimmt die Form der Kurve f(x) (gipfelig oder flach).
Biostatistik-5
3
Normalverteilung ― Beispiele
N(0,1)
Probabilit y
D ens it y
N(1,1)
F unc t ion
Probabilit y
y =norm al(x ; 0; 1)
D is t ribut ion F unc t ion
Probabilit y
p=inorm al(x ; 0; 1)
0. 6
D ens it y
F unc t ion
Probabil
y =norm al(x ; 1; 1)
1. 0
p
0. 6
1. 0
0. 5
0. 8
0. 5
0. 8
0. 4
0. 4
0. 6
0. 6
0. 3
0. 3
0. 4
0. 4
0. 2
0. 2
0. 2
0. 1
0. 2
0. 1
0. 0
0. 0
-2
-3
-1
0
1
2
3
-3
-2
-1
0
0. 0
1
2
Probabilit y D ens it y F unc t ion
3
-2
-3
0. 0
-1
0
1
2
3
-3
Probabilit y D is t ribut ion F unc t ion
y =norm al(x ; 0; 2)
p=inorm al(x ; 0; 2)
0. 6
1. 0
0. 5
0. 8
0. 4
0. 6
0. 3
0. 4
0. 2
0. 2
0. 1
0. 0
0. 0
-3
-2
-1
0
1
2
3
-3
Note: die Beugungspünkte
(Kehrpünkte) der Glockenkurve
sind bei μ ± σ
-2
-1
0
1
2
3
N(0,22)
Biostatistik-5
4
-2
-
Regel 68-95-99.7

Im Fall einer mit den Parameteren  und  charakterisierten
Normalverteilung:
 68% aller Messwerte haben eine einfache  Abweichung vom  Mittelwert
 95% aller Messwerte haben eine zweifache  Abweichung vom  Mittelwert
 99,7% aller Messwerte haben eine dreifache  Abweichung vom  Mittelwert
Prozentsatz der Werte in der
Population innerhalb eines
bestimmten Intervalls
Biostatistik-5
5
Das Bild der Verteilung aufgrund eines bestimmten
Mittelwertes und einer bestimmten Standardabweichung (SD)
(eine Normalverteilung angenommen)


In den Artikeln werden am
häufigsten das Mittelwert und
die Standardabweichung
dargestellt. Anhand dieser
Werte können wir uns
vorstellen, wie die Verteilung
aussehen kann
Z.B. Lebensalter (Jahre)
55.2  15.7
23.8
86.6
In diesem Intervall sind
95.44% der Werte
Biostatistik-5
6
Die Standardnormalverteilung N(0,1)

Verteilungsfunktion Ф(x) und Dichtefunktion φ(x) für
x
Z ~ N(0,1) : ( x )  P( Z  x )   (t ) dt, wo  ( x ) 


X 
1
2
e
x2

2

Standardisierung: Wenn X ~ N (  ,  2 ), dann Z 

und auch F ( x)  P( X  x)  P( Z  x )  ( x )
Rechnung von Wahrscheinlichkeiten mit Hilfe der
Standardnormalverteilung (a, b: reelle Konstanten):

~ N (0,1)
P( X  a)  1  P( X  a)  1  F (a)  1  ( a )
P( X  b)  F (b)  ( b )
P(a  X  b)  F (b)  F (a)  ( b )  ( a )
Biostatistik-5
7
Rechnungsbeispiel


In einer Population ist das Alter X normalverteilt:
X~ N(55,2; 15,72). Man berechne die
Wahrscheinlichkeit, daß das Alter zwischen 23,8
und 86,6 Jahre fällt.
Lösung: wir benutzen die Formel
P(a  X  b)  (
b 

)  (
a 

)
und die Tabelle der Standardnormalverteilung:
655, 2
23,855, 2
P(23,8  X  86,6)  ( 86,15
)


(
,7
15, 7 )
 (2)  ( 2)  0,97725  0,02275  0,9545  95,45%
Biostatistik-5
8
Dichtefunktion und Verteilungsfunktion der
Standardnormalverteilung
y=normal(x;0;1)
p=inormal(x;0;1)
0.6
1.0
0.5
0.8
0.4
φ(x)
Φ(x)
0.6
0.3
0.4
0.2
0.2
0.1
0.0
0.0
-3
Biostatistik-5
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
9
Tabelle der Standardnormalverteilung
(Auszug)
x
Ф(x): Fläche unter der Kurve links von x
-4
0.00003
-3
0.0013
-2.58
0.0049
-2.33
0.0099
-2
0.0228
Probability Density Function
Probability D
y =normal(x;0;1)
p=2*(1-inorm
0.6
1.0
0.5
0.8
0.4
0.6
0.3
-1.96
0.0250
-1.65
0.0495
-1
0.1587
0
0.5
1
0.8413
1.65
0.9505
1.96
0.975
2
0.9772
2.33
0.9901
2.58
0.9951
3
0.9987
4
0.99997
Biostatistik-5
0.4
0.2
0.2
0.1
0.0
-3
-1.96
0.025
-2
-1
0
0.95
1
1.96
0.0
2
3
-3
0.025
10
-2
-1
Zentraler Grenzwertsatz



Wenn wir aus einer (möglichst nicht normalverteilten) Population
mit Mittelwert  und Standardabweichung  eine Stichprobe x1,
x2, … xn entnehmen, können wir die Stichprobenelemente und
auch den aus denen berechneten Stichprobenmittelwert x
als
Zufallsvariablen betrachten.
Dann gelten die folgenden:
Erwartungswert des Stichprobenmittelwertes x ist auch der
Populationmittelwert, .
Standardabweichung des Stichprobenmittelwertes ist kleiner,
als die Standardabweichung der faktischen Population:

n


Für großen Stichprobenumfang n ist der Stichprobenmittelwert
annäherungsweise normalverteilt (unabhängig von der
Verteilung der faktischen Population)
Wenn  nicht gekannt ist, können wir die Standardabweichung
des Stichprobenmittelwertes mit dem
SD
Standardfehler (Standard Error) approximieren: SE 
n
Biostatistik-5
11
Illustration des zentrales Grenzwertsatzes
Biostatistik-5
12
SD oder SE?

55.2  15.7 (SD)

55.2  1.57 (SE, n=100)
Probability Density Func tion
y=normal(x;52.2;1.57)
1.0
0.26
0.24
0.8
0.22
0.20
0.18
0.6
0.16
0.14
0.12
0.4
0.10
0.08
0.06
0.2
0.04
0.02
0.00
20
23.8
86.6
In diesem Intervall sind
95.44% der Werte
Biostatistik-5
0.0
40
52.2
60
80
49
55.34
Der Erwartungswert liegt
mit 95.44% Wahrscheinlichkeit in diesem Intervall
13
Konfidenzintervalle
Statistische Schätzung




Der Parameter ist solch eine Nummer, die die Verteilung
der Population eindeutig charakterisiert.
Schätzung: anhand der Stichprobenwerte berechnen wir
die Nummer, sog. Statistik (statistic), die sich dem
entsprechenden Parameter der Population annähert.
Punkt-Schätzung: eine einzige Nummer
Z.B der Stichprobenmittelwert ist die Schätzung des μ (dem
unbekannten) Populationsmittelwertes.
n
x
x1  x 2 ... x n i 1
x

n
n
Biostatistik-5
i
nähert sich μ
15
Intervallschätzung, Vertrauensintervall
(Konfidenzintervall)




Intervallschätzung: ein von den Stichprobenelementen
berechnetes Intervall, das mit großer Wahrscheinlichkeit
den wahren (unbekannten) Wert des
Populationsparameters enthält
Die den Grad der Zuverlässigkeit bezeichnende
Wahrscheinlichkeit (Konfidenzniveau) hängt von uns ab.
Ihre Normalwerte: 0.90, 0.95, 0.99 )
Der "Fehler" der Schätzung (mit α bezeichnet) in
Abhängigkeit vom Konfidenzniveau
1-0.90=0.1, 1-0.95=0.05, 1-0.99=0.01
Das am häufigsten verwendete Konfidenzniveau ist 95%
(0.95), also für α wird am meistens der Wert α=0.05
verwendet.
Biostatistik-5
16
Illustrierung des Konfidenzintervalls mit den
fiktiven Wiederholungen des bestimmten
Experiments

Wenn wir das
Experiment in unserem
Gedanke hundertmal
wiederholten, würden
voraussichtlich 95 von
den 100 95%
Konfidenzintervallen
das Parameter der
Population enthalten
und 5 würden nicht.
Biostatistik-5
http://www.kuleuven.ac.be/ucs/java/index.htm
17
Berechnung des Konfidenzintervalls für den Mittelwert
μ einer Population mit Normalverteilung, wenn die
Standardabweichung σ der Population bekannt ist

Es kann demonstriert werden, dass
P( x z
also

n
( x  z

 μ  x z

n
, x  z
n

n
)  1
)
ist ein (1-α)100% Konfidenzintervall für μ.
Hier ist der Wert zα mit der Verteilungsfunktion Ф(x) der Standardnormalverteilung definiert:
( z )  ( z )  1   ,


wenn α=0.05, dann zα = 1,96
wenn α =0.01, dann zα = 2,576
95% Konfidenzintervall für μ:
Biostatistik-5
oder : ( z )  1  2
( x  1,96

n
, x  1,96

n
)
18
Rechnungsbeispiel

Wir möchten in einer Population die durchschnittliche Herzfrequenz
(per Minute) schätzen
 Nach der Untersuchung von 36 Patienten ist der Stichprobenmittelwert 90.
Die Standardabweichung der Population ist 15,5 (bekannt). Angenommen,
dass die Population normalverteilt ist, ist das 95% Konfidenz-intervall für
den Populationsmittelwert:


α=0,05, zα=1,96, σ=15,5

Die Untergrenze: 90 – 1,96·2,583 = 90+5,063 = 84,937

Die Obergrenze : 90 + 1,96·2,583 = 90+5,063 = 95,064

Das 95% Konfidenzintervall:

Das heißt, dass die Größe der Wahrscheinlichkeit, dass der wahre
(unbekannte) Populationsmittelwert im Intervall (84,94; 95,06) ist, ist
95%. Wir sind 95% sicher, dass der Mittelwert μ der Herzfrequenz in
diesem Intervall ist.
Biostatistik-5
σ/√n = 15,5/√36 =15,5/6 = 2,583
(84,94; 95,06)
19
Konfidenzintervall für den
Populationsmittelwert μ, wenn σ unbekannt ist


In diesem Fall substituieren wir σ mit der aus der Stichprobe berechneten
Standardabweichung
n
SD
Es ist beweisbar, dass
also
2
(
x

x
)
 i
i 1
n 1
SD
SD
P( x  t
   x  t
)  1
n
n
SD
SD
( x  t
, x  t
)
n
n
oder
( x  t SE, x  t SE)
ist ein (1-α)100% Konfidenzintervall für μ.

Hier kann tα von der Tabelle der Student-t-Verteilung ausgesucht werden,
der Freiheitsgrad = n -1
Biostatistik-5
20
Die Student-t-Verteilung
y=student(x;8)
0.5
1.0
0.4
0.8
0.3
0.6
0.2
0.4
0.1
0.2
0.0
0.0
-3
-2
-1
0
1
2
3
-3
Die t-Verteilung mit 8 Freiheitsgraden
Die blauen aussetzenden Linien zeugen die kritischen Werte ±tα für α=0,05.
Biostatistik-5
21
-
Die Student-t-Verteilung
y=student(x;20)
p
0.5
1.0
0.4
0.8
0.3
0.6
0.2
0.4
0.1
0.2
0.0
0.0
-3
-2
-1
0
1
2
3
-3
Die t-Verteilung mit 20 Freiheitsgraden
Biostatistik-5
22
-2
Die Student-t-Verteilung
y=student(x;100)
p
0.5
1.0
0.4
0.8
0.3
0.6
0.2
0.4
0.1
0.2
0.0
0.0
-3
-2
-1
0
1
2
3
-3
Die t-Verteilung mit 100 Freiheitsgraden
Biostatistik-5
23
-2
Tabelle der t-Verteilung
zweiseitiges Alpha
Freiheitsgrad
Biostatistik-5
0.2
0.1
0.05
0.02
0.01
1
3.077683537
6.313752
12.7062
31.82052
63.65674
2
1.885618083
2.919986
4.302653
6.964557
9.924843
3
1.637744352
2.353363
3.182446
4.540703
5.840909
4
1.533206273
2.131847
2.776445
3.746947
4.604095
5
1.475884037
2.015048
2.570582
3.36493
4.032143
6
1.439755747
1.94318
2.446912
3.142668
3.707428
7
1.414923928
1.894579
2.364624
2.997952
3.499483
8
1.39681531
1.859548
2.306004
2.896459
3.355387
9
1.383028739
1.833113
2.262157
2.821438
3.249836
10
1.372183641
1.812461
2.228139
2.763769
3.169273
11
1.363430318
1.795885
2.200985
2.718079
3.105807
24
Tabelle der t-Verteilung
zweiseitiges
Alpha
Freiheitsgrad
0.2
0.1
0.05
0.02
0.01
0.001
1
3.077683537
6.313752
12.7062
31.82052
63.65674
636.6192
2
1.885618083
2.919986
4.302653
6.964557
9.924843
31.59905
3
1.637744352
2.353363
3.182446
4.540703
5.840909
12.92398
4
1.533206273
2.131847
2.776445
3.746947
4.604095
8.610302
5
1.475884037
2.015048
2.570582
3.36493
4.032143
6.868827
6
1.439755747
1.94318
2.446912
3.142668
3.707428
5.958816
7
1.414923928
1.894579
2.364624
2.997952
3.499483
5.407883
...
…
…
…
…
…
…
100
1.290074761
1.660234
1.983971
2.364217
2.625891
3.390491
...
…
…
…
…
…
…
500
1.283247021
1.647907
1.96472
2.333829
2.585698
3.310091
...
…
…
…
…
…
…
1000000
1.281552411
1.644855
1.959966
2.326352
2.575834
3.290536
Biostatistik-5
25
Rechnungsbeispiel

Wir möchten in einer Population die durchschnittliche
Herzfrequenz (per Minute) schätzen
 Nach
der
Untersuchung
von
36
Patienten
ist
der
Stichprobenmittelwert 90, die Standardabweichung ist aufgrund
der Stichprobenwerte: SD=15,5. Angenommen, dass die
Population normalverteilt ist, ist das 95% Konfidenzintervall für den
Populationsmittelwert:







α=0,05, SD=15,5  SE = 15,5/√36 =15,5/6 = 2,583
Freiheitsgrad: df=n-1=36-1=35
tα=2,03
Die Untergrenze: 90  2,03 ·2,583 = 90  5,2444 = 84,755
Die Obergrenze: 90 + 2,03 ·2,583 = 90 + 5,2444 = 95,24
Das 95% Konfidenzintervall
(84,76; 95,24)
Das heißt, dass die Größe der Wahrscheinlichkeit, dass der
wahre (unbekannte) Populationsmittelwert im Intervall
(84,76, 95,24) ist, ist 95%. Wir sind 95% sicher, dass der
Mittelwert der Herzfrequenz in diesem Intervall ist.
Biostatistik-5
26
Rechnung mit SPSS:
Verfahren „Explorative Datenanalyse”
Biostatistik-5
27
Kontrollfragen-1









Parametern der Normalverteilung
Dichtefunktion der Normalverteilung
Regel 68-95-99,7 für Normalverteilung
Standardnormalverteilung, Standardisierung
Verteilungsfunktion der Standardnormalverteilung, Berechnung von
Wahrscheinlichkeiten
Es sei Z~N(0, 1). Geben Sie die folgenden Wahrscheinlichkeiten und stellen
Sie ihre Bedeutung aufgrund der Tabelle der Standardnormalverteilung
graphisch dar:
a) P(Z<0) b) P(Z>2) c) P(-1<Z<1)
X bezeichne den Wert vom Natrium [mmol/l] bei der laboratorischen
Bestimmung des Blutbildes. Seine Verteilung sei X~N(140, 2,52).
Berechnen Sie die Wahrscheinlichkeiten P(X<135), P(X>145) und
P(135<X<145)
Zentraler Grenzwertsatz
Standardfehler, wenn die Populationsstandardabweichung bekannt ist, und
wenn sie unbekannt ist
Biostatistik-5
28
Kontrollfragen-2






Unterschied zwischen Punktschätzung und Intervallschätzung
Konfidenzintervall für den Mittelwert m einer Population mit
Normalverteilung, wenn die Standardabweichung σ der Population bekannt
ist
Eine Stichprobe entnommen von einer normalverteilten Population mit
Standardabweichung s=2,5 hat Elementzahl 25, Mittelwert 141 und
Standardabweichung 3,5. Berechnen Sie das 95% Konfidenzintervall für
den Populationsmittelwert (der nötige Tabellenwert ist 1,96).
Konfidenzintervall für den Mittelwert m einer Population mit
Normalverteilung, wenn die Standardabweichung σ der Population
unbekannt ist
Eine Stichprobe entnommen von einer normalverteilten Population hat
Elementzahl 25, Mittelwert 141 und Standardabweichung ist 3,5. Wie groß
ist der Freiheitsgrad? Erstellen wir ein 95% Konfidenzintervall für den
Populationsmittelwert (der nötige Tabellenwert ist 2,064).
Was für eine Wahrscheinlichkeit drückt das Konfidenzniveau aus? Z.B.
95%?
Biostatistik-5
29