11.3. Variablentrennung, Ähnlichkeit und Trajektorien
Werbung
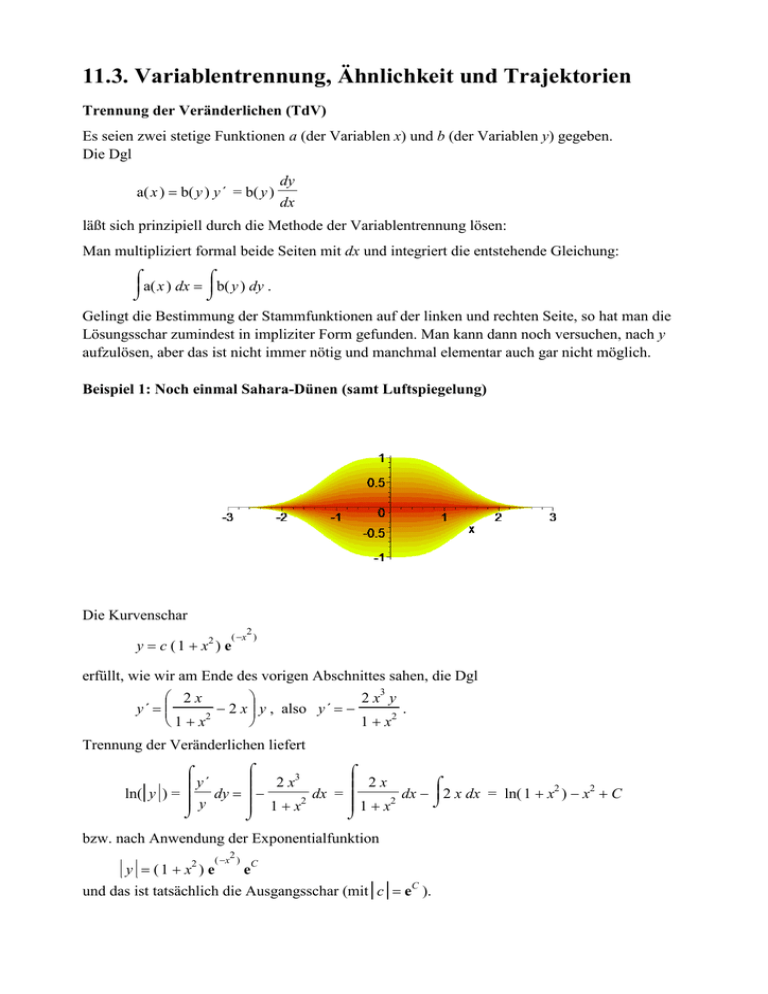
11.3. Variablentrennung, Ähnlichkeit und Trajektorien Trennung der Veränderlichen (TdV) Es seien zwei stetige Funktionen a (der Variablen x) und b (der Variablen y) gegeben. Die Dgl a( x ) = b( y ) y´ = b( y ) dy dx läßt sich prinzipiell durch die Methode der Variablentrennung lösen: Man multipliziert formal beide Seiten mit dx und integriert die entstehende Gleichung: ⌠ ⌠ a( x ) dx = b( y ) dy . ⌡ ⌡ Gelingt die Bestimmung der Stammfunktionen auf der linken und rechten Seite, so hat man die Lösungsschar zumindest in impliziter Form gefunden. Man kann dann noch versuchen, nach y aufzulösen, aber das ist nicht immer nötig und manchmal elementar auch gar nicht möglich. Beispiel 1: Noch einmal Sahara-Dünen (samt Luftspiegelung) Die Kurvenschar y = c ( 1 + x2 ) e 2 ( −x ) erfüllt, wie wir am Ende des vorigen Abschnittes sahen, die Dgl 2x 2 x3 y y´ = − 2 x y , also y´ = − . 1 + x2 1 + x2 Trennung der Veränderlichen liefert ⌠ ⌠ ⌠ 2 x3 2x y´ ⌠ − ln( y ) = d y = d x = dx − 2 x dx = ln( 1 + x2 ) − x2 + C 2 2 ⌡ y 1 + x 1+x ⌡ ⌡ ⌡ bzw. nach Anwendung der Exponentialfunktion y = (1 + x ) e 2 2 ( −x ) eC und das ist tatsächlich die Ausgangsschar (mit c = eC ). Ähnlichkeits-Differentialgleichungen sind von der Form y y´ = g . x Sie verdanken ihren Namen der Eigenschaft, daß mit jeder Lösungskurve y = f( x ) auch alle dazu ähnlichen Kurven, die durch gleich starke Streckung bzw. Stauchung in beiden Koordinatenrichtungen entstehen, wieder Lösungen darstellen. Denn für die gestreckte bzw. gestauchte Kurve c y = f( c x ) , d.h. y= f( c x ) c (c ≠ 0) gilt ja f( c x ) y = g . y´ = f ´( c x ) = g cx x Beispiel 2: Steigungsdreiecke und radiales Richtungsfeld Zu den einfachen Spezialfällen gehört die Ähnlichkeits-Dgl y´ = y x wo das jeweilige Steigungsdreieck ähnlich zu dem Dreieck ist, das von den Koordinatenabschnitten gebildet wird. y( x ) = c x Mit Ausnahme der y-Achse haben die Geraden durch den Ursprung die Gleichung y=cx. Ableiten ergibt y´ = c, und die Geradenschar wird daher beschrieben durch die Dgl y = x y´ bzw. y´ = y x . Umgekehrt kann man die Dgl sofort durch Trennung der Veränderlichen lösen: ⌠ ⌠ 1 1 dy = dx , ln( y ) = ln( x ) + C , y x ⌡ ⌡ C y =e x , y=cx. Beispiel 3: Steigungsdreiecke und hyperbolisches Richtungsfeld Wechselt man in der Dgl aus Beispiel 2 das Vorzeichen der rechten Seite, so hat diese kleine Ursache große Wirkung: Die Lösungen der Dgl y´ = − y x sind jetzt die Hyperbeln y= c x , wie man leicht nachprüft. Hier sind die Steigungsdreiecke zwar wieder ähnlich zu den Dreiecken mit den Koordinatenabschnitten als Katheten, aber die "Orientierung" ist jetzt umgekehrt. y( x ) = c x Beispiel 4: Konzentrische Kreise um den Ursprung werden beschrieben durch die Gleichung x 2 + y 2 = r2 , wobei r der Radius-Parameter ist. Differentiation nach x ergibt unter Beachtung der Tatsache, daß y von x abhängt: 2 x + 2 y y´ = 0 bzw. y´ = − x y . Auch diese Dgl kann man umgekehrt durch Trennung der Variablen lösen: y2 x2 ⌠ ⌠ y dy = −x dx , =− + c , x2 + y2 = 2 c , ⌡ ⌡ 2 2 und das ergibt mit 2 c = r2 wieder die Ausgangsgleichungen. Offenbar schneiden die Ursprungsgeraden alle konzentrischen Kreise senkrecht, was sich in den y zugehörigen Differentialgleichungen dadurch widerspiegelt, daß im einen Fall y´ = , im anderen x x dagegen y´ = − gilt. Mit anderen Worten: Die Orthogonaltrajektorien der Ursprungsgeraden y sind die konzentrischen Kreise, und umgekehrt. Allerdings wird die senkrechte Gerade x = 0 hierbei nicht erfaßt. Reduktion von Ähnlichkeits-Differentialgleichungen Jede Ähnlichkeits-Dgl y y´ = f x kann man durch die Substitution z = y x bzw. x z = y in eine Dgl y´ = z + x z´ = f( z ) bzw. x z´ = f( z ) − z umformen, die sich prinzipiell wieder durch Trennung der Variablen lösen läßt: Wir dürfen den Fall f( z ) = z (den wir in Beispiel 2 schon erledigt hatten) ausschließen und bekommen dann ⌠ ⌠ 1 1 dz = dx = ln( x ) + c . f( z ) − z x ⌡ ⌡ ⌠ 1 Für jede Stammfunktion G( z ) = dz auf der linken Seite ist dann f( z ) − z ⌡ y G = ln( x ) + c , x womit zumindest eine implizite Gleichung zwischen x und y gefunden ist. Beispiel 5: Hyperbeln im Richtungsfeld Die Ähnlichkeits-Differentialgleichung y y´ = y+x y−x = x y x +1 −1 geht mit der Substitution y = x z , y´ = z + x z´ über in x z´ = z+1 z−1 −z 2 + 2 z + 1 −z= z−1 . Mittels Trennung der Variablen gelangt man zu ln( z2 − 2 z − 1 ) = −2 ln( x ) + c z2 − 2 z − 1 = ec 2 x und y2 − x y − x2 = ec . Das ist eine gedrehte Hyperbelschar (vergleichen Sie Beispiel 3)! Isogonale Trajektorien sind Kurven, die eine gegebene Kurvenschar unter einem festen Winkel α zwischen 0 und π/2 schneiden (isogonal = gleichwinklig). Im Falle α = π/2 sind das gerade die orthogonalen Trajektorien, im Fall α = 0 werden die Trajektorien zu Tangenten. In allen anderen Fällen muß man darauf achten, ob der Schnittwinkel von der Kurve zur Trajektorie oder umgekehrt gemessen wird. Wir wollen annehmen, daß man von der Trajektorie zur Kurve durch eine Drehung im Uhrzeigersinn um weniger als π/2 gelangt. Wird die ursprüngliche Kurvenschar durch eine explizite Dgl y´ = f( x, y ) beschrieben, so erhält man eine Dgl für die isogonalen Trajektorien zum Schnittwinkel α < π/2 : a + f( x, y ) y´ = 1 − a f( x, y ) mit a = tan( α ). Denn ist y´ = tan( β ) die Steigung der ursprünglichen Kurve, so ist tan( α ) + tan( β ) tan( α + β ) = 1 − tan( α ) tan( β ) die Steigung der isogonalen Trajektorie durch den Schnittpunkt. Beispiel 6: Wirbel Wir suchen diejenigen Kurven, die sämtliche Ursprungsgeraden unter dem gleichen Winkel α < π /2 schneiden. Da die Geradenschar die Dgl y´ = y x löst, erfüllen die isogonalen Trajektorien die Dgl a+ y´ = 1− y x ay = ax+y x−ay mit a = tan( α ) . x Das ist eine Ähnlichkeits-Dgl, die man durch die Substitution z= y x bzw. y = x z löst. Es ist dann y´ = z + x z´ = a+z 1−az bzw. dz dx = a ( z2 + 1 ) x (1 − a z) Mittels Trennung der Veränderlichen gelangt man zu . ⌠ ⌠ ⌠ 1 az a dx , d z − d z = x z2 + 1 z2 + 1 ⌡ ⌡ ⌡ arctan( z ) − a ln( z2 + 1 ) 2 Mit der Substitution z = y x = a ln( x2 ) 2 +C. bedeutet das y a ln( x2 + y2 ) arctan − =C x 2 oder in Polarkoordinaten ausgedrückt: φ − a ln( r ) = C bzw. r = c e φ a (mit c = e C a ). Die Lösungen sind wieder einmal logarithmische Spiralen, und ihre isogonalen Trajektorien sind hier zugleich Isoklinen (nämlich die Geraden durch den Ursprung). Die gezeichneten Richtungsfelder haben einen kleinen Schönheitsfehler: Da MAPLE offenbar alle Pfeile von links nach rechts ausrichtet, muß man oberhalb der Geraden mit Steigung a alle Pfeile umdrehen, um ein echtes Wirbelfeld zu erhalten. Sehr viel eleganter und kürzer wird die Sache, wenn man von Anfang an mit Polarkoordinaten arbeitet. Man hat dann die Dgl rdφ dr = tan( α ) = a zu lösen, und das geht ruckzuck mittels Variablentrennung : ⌠ ⌠ 1 1 = dφ = dr = ln( r ) − ln( c ), a a r ⌡ ⌡ φ φ a r=ce . Für x = r cos( φ ) und y = r sin( φ ) erhalten wir wegen dr dφ = r a das folgende System von Differentialgleichungen: dx dφ dy = −r sin( φ ) + dr cos( φ ) = −y + x dφ a dr y = r cos( φ ) + sin( φ ) = x + dφ dφ a Das hierzu von MAPLE gezeichnete Richtungsfeld ist nun tatsächlich ein zyklisches Wirbelfeld (vgl. Beispiel 2 in Abschnitt 8.2): a=1 x´( φ ) = −y( φ ) + x( φ ), y´( φ ) = x( φ ) + y( φ ) Beispiel 7: Expansion des Weltalls Wir stellen uns vor, n Sterne seien auf die Ecken eines regelmäßigen n-Ecks verteilt, und jeder bewege sich von dem im Uhrzeigersinn nächsten mit gleichmäßiger Geschwindigkeit weg. Der Winkel zwischen ihrem Radialvektor und ihrer Bewegungsrichtung ist dann immer π 2 − π n . Daher sind die Bahnkurven Isogonaltrajektorien zu den Geraden durch den Ursprung mit π a = tan . n n=3 n=4 n=5 Pfeile im Bereich links oben umdrehen! Welchen Weg haben die Sterne seit dem "Urknall" (φ = −∞) zurückgelegt, wenn ihr Abstand vom Zentrum r ist? Um dies zu beantworten, müssen wir die Bogenlänge ihrer Bahnkurve bestimmen: φ a Für r = c e dr ist dφ φ a = ce a und ds dφ φ 2 dr a + r2 = c e dφ = 1 a2 + 1. Daraus berechnen wir die Bogenlänge φ s=c ⌠ t a + 1 e dt = c 2 a ⌡ 1 φ a 1 + a2 e −∞ und erhalten den erstaunlichen Zusammenhang r s = 1 1 + a2 2 π = 1 + tan n 1 − 2 π = cos . n Mit anderen Worten: Der Weg ist genau so lang, wie wenn sich der Stern tangential geradeaus bis zum Schnitt mit der Senkrechten zum Radiusvektor bewegt hätte. Im Spezialfall n = 4 (Quadrat) ist die Weglänge also gleich groß wie der Abstand zweier benachbarter Sterne! n=4 n=7 n = 12