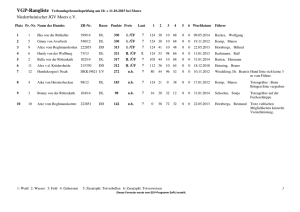
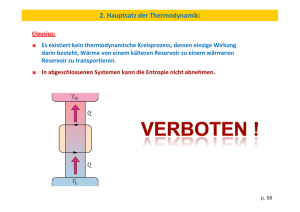
Maxwellscher Dämon, Landauers Principle, Thermodynamics and
Werbung

Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen TU Berlin Sommersemester 2012 Inhaltsverzeichnis Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon 1 Maxwellscher Dämon 2 Historie 3 Landauer-Prinzip 4 FPE Speichermodell Historie LandauerPrinzip 5 Aktuelle Forschung FPE Speichermodell Aktuelle Forschung Quellen 6 Quellen Idee des Maxwellschen Dämons 1871 Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Gedankenexperiment um den zweiten Hauptsatz der Thermodynamik zu entkräften bzw. ihn in Frage zu stellen Dämon separiert schnelle und langsame Moleküle Ideale Bedingungen: werder Messung noch Bedienen der Klappe kostet Energie Dämon schafft Ordnung in Form Temperaturdifferenz → 2. HS TD verletzt Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Abbildungsquelle: Htkym, 2007, CC by 3.0, wikimedia.org Mechanischer Dämon von Smoluchowski Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Funktioniert nicht wegen Fluktuationen Abbildungsquelle: John D. Norton, Waiting for Landauer, 2011 Szilárd, 1929 Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen (a) Position unbekannt (b) Trennwand einfügen, misst Position (c) Gewicht an Trennwand Messung sollte Entropie mit kB ln 2 kosten Abbildungsquelle: The physics of Maxwell’s demon and information, Koji Maruyama, Franco Nori, Vlatko Vedral, 2008 Brillouin, 1951 Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Annahme, dass der Dämon das Molekül „sehen“ muss Explizite Berechnung der Entropiekosten bei der Messung mit Licht Informationsbeschaffung impliziert Entropiezunahme, sodass 2. HS der TD nicht verletzt wird Quellen Abbildungsquelle: Maxwell´s Demon, Entropy, Information, Computing, 1990 Landauer und Bennett, 1961/1982 Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Landauer zeigte 1962, dass das Löschen von Information die Entropie von kB T ln 2 freisetzen muss Bekannt als „Landauer-Prinzip“ Bennett zeigte, dass die Messung ohne Entropieerhöhung stattfinden kann Er schloss daraus 1982, dass das Löschen der Information Maxwells Dämon unmöglich macht Speichermodell Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Kasten in dem ein einzelnes Molekül eines idealen Gases gefangen ist Eingebettet in ein Wärmereservoir bei T=const Trennwand kann eingezogen werden Trennwand kann als Kolben fungieren und das Molekül adiabatisch komprimieren/expandieren Thermodynamische Kosten Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie Ideale Gasgleichung; N = 1, T = const pV = Nkb T kb T dV = −δQ (2) V Bei der Kompression vom Volumen V1 auf das Volumen V2 wird also folgende Arbeit verrichtet: δW = −pdV = − LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen (1) Z V2 ∆W = − V1 kb T V2 dV = −kb T ln( ) V V1 (3) Messung Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Speicher befindet sich vor der Messung (a) im Zustand ’0’. Ergebnis ’0’: Speicher im korrekten Zustand (b, c, oben) Ergebnis ’1’: Speicher muss Zustand wechseln (b, c, unten) Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Erfolgt durch adiabatische Expansion/Kompression b, unten: Arbeit ∆W = −kb T ln(2) wird frei c, unten: ∆W = +kb T ln(2) wird aufgebraucht Insgesamt keine Energiekosten. Löschen Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Vor dem Löschen (a) ist der Zustand nicht bekannt Trennwand wird herausgezogen (b) Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Teilchen im ganzen Kasten (c) Adiabatische Kompression auf Zustand ’0’ Arbeit ∆W = +kb T ln(2) wird aufgebraucht Für das ’Löschen’ von einem Bit wird die Wärme kb T ln(2) benötigt! Bekannt als das ’Landauer-Prinzip’ Teilchen im bistabilen Potential Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Verallgemeinerung auf ein brownsches Teilchen im bistabilen Potential Kann zwei Zustände annehmen: 1 oder 0 Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Abbildungsquelle: Heat generation required by information erasure, Shizume, 1995 Brownsche Bewegung Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Beschreibung der Bewegung des Teilchens erfolgt durch die Langevin Gleichung: Langevin Gleichung Sonja Molnos, André Röhm, Maren Schiersch m Maxwellscher Dämon d 2x dx ∂V (x, t) + mγ =− + FR (t) 2 dt dt ∂x Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen m Masse des Teilchens γ Reibungskoeffizient V (x, t) das Potential FR (t) Rauschterm (4) Fokker-Planck-Gleichung Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Annahme: Gaußsches weißes Rauschen (hFR (t1 ) FR (t2 )i = 2mγT δ (t1 − t2 )) Langevin-Gleichung kann in FPE umgeschrieben werden Fokker-Planck-Gleichung Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen ∂f ∂ ∂ 1 ∂V γT ∂ 2 = − u+ γu + + f ∂t ∂t ∂u m ∂x m ∂u 2 (5) Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Unter Verwendung des ersten Hauptsatzes und der FPE: d hE i − Ẇ mit (6) dt Z ∞ ∂V mu 2 ∂V E≡ + V (x, t) , s Ẇ = = dxdu f 2 ∂t ∂t −∞ Q̇ = Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Z ∞ Q̇ = dxdu −∞ ∂f (x, u, t) V (x, t) = γ T − mu 2 ∂x (7) Shannon-von-Neumann-Entropie Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Z ∞ S ≡− dxdu f ln f (8) −∞ Unter Verwendung der FPE, erhält man die Ableitung : # " * + dS T ∂ ln f 2 =γ −1 dt m ∂u (9) Ungleichung der Wärmeproduktion Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen dS γ Q̇ − T =− dT m ⇔ Q̇ ≤ T * dS dt ∂ ln f T + mu ∂u 2 + ≤0 (10) Wärmeproduktion Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Daher erhält man die unterste Grenze für den Wärmetransport zwischen zwei Zeiten ti und tf : Z tf ∆Qout (ti , tf ) = −Q̇ dt ≥ T [S (ti ) − S (tf )] (11) ti Betrachtung eines Ensembles bestehend aus N (N >> 1)Speicher zum Zeitpunkt ti speichert jedes Ensemble ein Bit Einführung der Verteilungsfunktionen f0 (x, t) und f1 (x, t) für die Speicherwerte 1 und 0 Einführung p1 N und p2 N als die Anzahl der Teilchen im Speicher, welche die Werte 1 und 0 besitzen. Entropie am Anfang Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Shannon-von-Neumann-Entropie für ein Ensemble pro Speicher gegeben durch: Z dudxp0 f0 ln (p0 f0 + p1 f1 ) + p1 f1 ln (p0 f 0 + p1 f1 ) ∞ (12) ≈ p0 S [f0 ] + p1 S [f1 ] + S [p0 , p1 ] , Maxwellscher Dämon Historie ∞ Sinit = − wobei LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen (13) Z ∞ S [fk ] ≡ − dxdufk ln fk (k = 0 oder 1) (14) pi ln pi (15) −∞ S [p0 , p1 ] ≡ − X i=0,1 Minimale Entropiekosten Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Unter der Voraussetzung, dass der Speicher nach der Löschung sofort wieder eindeutige Werte annimmt, und der Anteil der Speicher im Zustand ’0’, bzw. ’1’ sich nicht ändert, lautet die Entropie: Sset = p0 S [f0 ] + p1 S [f1 ] (16) ⇒ ∆Qout (ti , tf ) = T (Sinit − SSet ) = TS [p0 , p1 ] (17) Sagawa und Ueda Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Takahiro Sagawa und Masahito Ueda (2008) Neues Ergebnis, in voller Quantenmechanik Wir betrachten ihr klassisches Analogon Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Wichtigster Unterschied: Asymmetrischer Speicher mit V1 /Vges = t Messung Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information analoge Schritte zu Landauers Speicher Messung von einem Bit (P(’0’) = P(’1’) = 1/2) Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Ergebnis ’0’ erzeugt wieder keine Kosten, aber: b, unten: Arbeit ∆W = −kb T ln( 1t ) wird frei 1 c, unten: ∆W = +kb T ln( 1−t ) wird aufgebraucht t Zusammen kostet das: ∆W = +kb T ln( 1−t ) Über beide mögliche Ergebnisse gemittelt: t ∆Wmes = + kb2T ln( 1−t ) Löschen Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Vor dem Löschen (a) ist der Zustand nicht bekannt Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie Wand wird zur Mitte verschoben (a) LandauerPrinzip Dies kostet ∆W = + kb2T [ln(2t) + ln(2(t − 1))] FPE Speichermodell Teilchen im ganzen Kasten (c) Aktuelle Forschung d: Arbeit ∆W = −kb T ln(t) wird aufgebraucht Quellen Das Löschen kostet ∆Weras = kb T ln(2) − kb T t 2 ln( 1−t ) Gesamtkosten Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon ∆Weras = kb T ln(2) − kb T t 2 ln( 1−t ) t ) ∆Wmes = + kb2T ln( 1−t ∆Weras + ∆Wmes = kb T ln(2) Für Symmetrisches Potential, d.h. t=1/2 ergibt sich Landauers Überlegung Historie Sonst weicht es jedoch ab, z.b. für t=4/5 ist ∆Weras = 0 LandauerPrinzip Die Wärme wird also bei der Datenverarbeitung eines Bits durch Messung und Löschen gemeinsam emittiert. FPE Speichermodell Aktuelle Forschung Quellen Quellenangabe Maxwellscher Dämon, Landauers Principle, Thermodynamics and Information Sonja Molnos, André Röhm, Maren Schiersch Maxwellscher Dämon Historie LandauerPrinzip FPE Speichermodell Aktuelle Forschung Quellen Maxwell´s Demon, Entropy, Information, Computing, 1990 The physics of Maxwell’s demon and information, Koji Maruyama, Franco Nori, Vlatko Vedral, 2008 Heat generation required by information erasure, Shizume, 1995 Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Information Erasure, Sagawa, Ueda, 2009