Anorganische Chemie I 1. OÜ PD Dr. A. Mezzetti Fragenkatalog VI

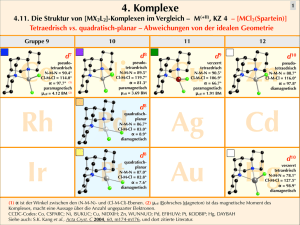
Anorganische Chemie I
PD Dr. A. Mezzetti
1. OÜ
Fragenkatalog VI
Abgabetermin: 4.11.2008
1. Aufgabe
Triphenylphosphin reagiert mit NiBr2·3H2O in siedendem Butanol unter Bildung eines dunkelgrünen, paramagnetischen Komplexes A (µeff=2.97 BM). Komplex A ist neutral und enthält Ni,
Br und PPh3. Die Elementaranalyse lautet: 58.25 % C, 4.2 % H, 21.60 Br. Der analoge Komplex
B mit P(CH3)3 ist dunkelrot und diamagnetisch.
– Empirische Formel von A? (1 Punkt)
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in A und B? (1 Punkt)
– Diskutieren Sie die Struktur von A und B anhand des VB-Modells! (1 Punkt)
– Diskutieren Sie die Struktur von A und B anhand des KFT-Modells! (1 Punkt)
– Vergleichen Sie die Eigenschaften von A und B und erklären Sie die Unterschiede! (1 Punkt)
2. Aufgabe
[Fe(CO)5] (C), ein diamagnetischer Komplex, reagiert mit OH– unter Bildung von [Fe(CO)4]2–
(D).
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in C und D? (2 Punkte)
– Diskutieren Sie die Struktur von C und D anhand des VB-Modells! (2 Punkte)
– Diskutieren Sie die Struktur von D anhand des KFT-Modells! Ist dieser Ansatz in diesem Fall
nützlich? (1 Punkt)
3. Aufgabe
Disproportionierung von Co(II) zu Co(I) und Co(III) wird durch bestimmte P(OR)3-Liganden
ausgelöst:
2 Co2+ + 11 P(OR)3 → [Co(P(OR3))5]+ (E) + [Co(P(OR3))6]3+ (F)
Komplex E ist trigonal-bipyramidal. E und F sind beide diamagnetisch.
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in E und F? (1 Punkt)
– Diskutieren Sie die Struktur von E und F anhand des VB-Modells! (1 Punkt)
– Diskutieren Sie die Struktur von F anhand des MO-LCAO-Modells (nur σ-Bindung)! (1 Punkt)
– Anhand der KFT entwerfen Sie ein qualitatives Aufspaltungsmuster für die Energien der dOrbitale. Wieso ist E diamagnetisch? (2 Punkte)
1. Aufgabe
Triphenylphosphin reagiert mit NiBr2·3H2O in siedendem Butanol unter Bildung eines dunkelgrünen, paramagnetischen Komplexes A (µeff=2.97 BM). Komplex A ist neutral und enthält Ni,
Br und PPh3. Die Elementaranalyse lautet: 58.25 % C, 4.2 % H, 21.60 Br. Der analoge Komplex
B mit P(CH3)3 ist dunkelrot und diamagnetisch.
– Empirische Formel von A? (1 Punkt)
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in A und B? (1 Punkt)
– Diskutieren Sie die Struktur von A und B anhand des VB-Modells! (1 Punkt)
– Diskutieren Sie die Struktur von A und B anhand des KFT-Modells! (1 Punkt)
– Vergleichen Sie die Eigenschaften von A und B und erklären Sie die Unterschiede! (1 Punkt)
–
Empirische Formel von A aus der Elementaranalyse (1 Punkt):
100 g Komplex enthalten:
m(X)
n(X)
n(X)/n(Br)
58.25 g C
4.850 mol C
17.9
4.2 g H
4.17 mol H
15.4
21.60 g Br
0.2703 mol Br
1
Das Molverhältnis zeigt, dass 1 Mol Br auf ein Mol PPh3 entfällt. Somit ist die Summenformel [NiBr2(PPh3)2], weil der neutrale Komplex 2 Bromliganden enthalten muss. Die
prozentuale Zusammensetzung ist C, 58.19 %, H, 4.07 %, Br, 21.51.
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in A und B? (1 Punkt)
Ni(II) → d8
–
16 Elektronen
für beide Komplexe
Diskutieren Sie die Struktur von A und B anhand des VB-Modells! (1 Punkt)
4L
high-spin d8
Komplex A:
d
low-spin d8
s
px py pz
4L
Komplex B:
d
–
sp3, tetraedrisch
s
px py pz
dsp2, quadratisch planar
Diskutieren Sie die Struktur von A und B anhand des KFT-Modells! (1 Punkt)
Vierfach-koordinierte Komplexe können entweder tetraedrisch oder planar-quadratisch sein:
[NiBr2(PPh3)2] und [NiBr2(PMe3)2] haben beide die d8-Elektronenkonfiguration aber unterschiedliche Eigenschaften. Das qualitative Aufspaltungsdiagramm zeigt, dass tetraedrische
Komplexe Licht mit grösseren Wellenlängen absorbieren als planar-quadratische Komplexe.
Der grüne Komplex [NiBr2(PPh3)2] absorbiert rotes Licht (niedrigere Energie), die rote Farbe
von [NiBr2(PMe3)2] stammt aus der Absorption im grünen Bereich (höhere Energie). Somit
könnte [NiBr2(PPh3)2] tetraedrisch sein, [NiBr2(PMe3)3] planar-quadratisch. Die magnetischen Eigenschaften der beiden Komplexe erhärten diese Hypothese (siehe Schema).
2. Aufgabe
[Fe(CO)5] (C), ein diamagnetischer Komplex, reagiert mit OH– unter Bildung von [Fe(CO)4]2–
(D).
[Fe(CO)5] (C)
!CO 2
OH –
–
#
!!!" [Fe(COOH)(CO)4] """"
[FeH(CO)4]–
2–
OH –
!!!!
" [Fe(CO)4]
–H 2O
(D)
– Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in C und D? (2 Punkte):
Komplex C:
Fe(0)
d8
18 Elektronen
Komplex D:
Fe(–2)
d10
18 Elektronen
– Diskutieren Sie die Struktur von C und D anhand des VB-Modells! (2 Punkte)
CO ist ein stark-Feld-Ligand. Deshalb erwarten wir low-spin-Komplexe. Somit bleibt in der
d8-Elektronenkonfiguration ein d-Orbital unbesetzt:
5L
low-spin d8
Komplex C:
dsp3
d
s
px py pz
4L
s
px py pz
d10
Komplex D:
d
sp3, tetraedrisch
Das VB-Modell sagt nichts darüber aus, ob Komplex C quadratisch-pyramidal oder trigonalbipyramidal ist. Wir werden in einer späteren Übung sehen, dass π-Akzeptor-Liganden die
trigonale-bipyramidale Struktur stabilisieren.
Wegen seiner d10- Elektronenkonfiguration kann Komplex D nur tetraedrisch sein.
– Diskutieren Sie die Struktur von D anhand des KFT-Modells! Ist dieser Ansatz in diesem Fall
nützlich? (1 Punkt)
Das VB-Modell besagt, dass Komplex D als d10-System tetraedrisch und diamagnetisch ist
(siehe oben). Hingegen ist der KFT-Ansatz für solche Komplexe nicht hilfreich, da die
gesamte LFSE = 0 ist:
t2 (xy, xz, yz)
!t
e (z2, x2–y2)
3. Aufgabe
Disproportionierung von Co(II) zu Co(I) und Co(III) wird durch bestimmte P(OR)3-Liganden
ausgelöst:
2 Co2+ + 11 P(OR)3 → [Co(P(OR3))5]+ (E) + [Co(P(OR3))6]3+ (F)
Komplex E ist trigonal-bipyramidal. E und F sind beide diamagnetisch.
–
–
Oxidationszahl, Elektronenkonfiguration und gesamte Elektronenzahl in E und F? (1 Punkt):
Komplex E:
Co(I)
d8
18 Elektronen
Komplex F:
Co(III)
d6
18 Elektronen
Diskutieren Sie die Struktur von E und F anhand des VB-Modells! (1 Punkt):
5L
low-spin d8
Komplex E:
dsp3
d
low-spin d6
s
px py pz
6L
Komplex F:
d
s
px py pz
d2sp3, oktaedrisch
Wie oben erwähnt, sagt das VB-Modell nichts darüber aus, ob Komplex E quadratischpyramidal oder trigonal-bipyramidal ist. Wir werden in einer späteren Übung sehen, dass πAkzeptor-Liganden die trigonale-bipyramidale Struktur stabilisieren.
–
Diskutieren Sie die Struktur von F anhand des MO-LCAO-Modells (nur σ-Bindung)! (1
Punkt):
Komplex F ist low-spin d6, was auf die t2g6e0-Elektronenkonfiguration hinweist. Das σbindende MO-LCAO-Schema zeigt, dass die nicht-bindenden t2g-Orbitale vollständig besetzt
sind, die σ-antibindenden eg-Orbitale bleiben aber unbesetzt:
(Zusatzinformation / Update (nicht notenwirksam!): Wie gelernt, werden die t2g-Orbitale
durch π-Akzeptoren stabilisiert. Dies stabilisiert Komplex F zusätzlich)
– Anhand der KFT entwerfen Sie ein qualitatives Aufspaltungsmuster für die Energien der dOrbitale von E (sorry, fehlt in der Aufgabestellung!). Wieso ist E diamagnetisch? (2 Punkte):
Aus der Charaktertafel erkennt man, dass die d-Orbitalen in drei Sätzen aufgespaltet werden:
(a’1: z2; e’: x2–y2, xy; e’’: xz, yz)
Ein qualitatives Aufspaltungsmuster für die Energien der d-Orbitale eines fünffach-koordinierten Komplexes mit D3h-Symmetrie kann man durch das Entfernen eines Liganden
aus einem oktaedrischen Komplex entwickelt werden.
Zuerst soll man bemerken, dass in der trigonalen bipyramidalen Struktur die d(x2–y2)- und
d(xy)–Orbitale entartet sind. Somit besitzen sie die gleiche Energie. Gegenüber dem
oktaedrischen Komplex wird das d(x2–y2)-Orbital stark stabilisiert, weil ein Ligand
vollständig entfernt, und ein weiterer zur Überlappung mit dem d(xy)-Orbital gebracht wird.
Dadurch steigt die Energie des d(xy)-Orbitals an. In der D3h-symmetrischen Struktur sind die
Energien der d(x2–y2)- und d(xy)–Orbitale gleich:
Oh
D3h
L
L
L
M
L
L
L
Oh
–L
D3h
L
L
M
L
L
L
für d8:
a1 '
a1'
e'
e'
e''
e''
(siehe Skript, S. 98)
Der Komplex ist diamagnetisch, weil die 8 Elektronen nur die e’- und e’’-Orbitale besetzen.
Obwohl die a1’–e’-Energiedifferenz kleiner ist als die eg–t2g-Aufspaltung in einem oktaedrischen Komplex, ist P(OR)3 ein stark-Feld-Ligand und stabilisiert low-spin-Komplexe.
Kommentar:
Beim genaueren Hinsehen der Tabelle im Skript erkennt man, dass alle Wechselwirkungen –
entweder Stabilisierungen oder Destabilisierungen – in der TBP-Struktur kleiner sind als im
ursprünglichen oktaedrischen Komplex.
KFT-Erklärung: Trigonal-bipyramidalen Komplexen enthalten fünf anstatt sechs Liganden,
die weniger "gezielt" auf die Orbitale gerichtet sind. Die Situation in der trigonalen Ebene
(xy-Ebene) ist entscheidend: 3 Liganden destabilisieren 2 Orbitale (e'). In oktaedrischen
Komplexen destabilisieren 4 Liganden nur 1 Orbital (x2–y2)!
MO-LCAO-Erklärung: In oktaedrischen Komplexen sind 2 Orbitale σ-antibindend, in trigonal-bipyramidalen Komplexen sind 3 Orbitale σ-antibindend. Somit sind die antibindende
Wechselwirkungen in den TBP-Komplexen auf mehr Orbitale verteilt, was die Energiedifferenz zwischen nichtbindenden und antibindenden Orbitalen verkleinert.