Verteilungen

Verteilungen
Session 5
1
Verteilungen in R
Das R System kennt viele Verteilungen, darunter praktisch alle Standardverteilungen, denen man üblicherweise in Einführungskursen in die Statistik begegnet. Die entsprechenden Befehle in R lauten
Verteilung
beta
binomial
Cauchy
chi-squared
exponential
F
gamma
geometric
hypergeometric
log-normal
logistic
negative
normal
Poisson
Student s t
uniform
Weibull
Wilcoxon
Funktionsname
beta
binom
cauchy
chisq
exp
f
gamma
geom
hyper
lnorm
logis
binomial
norm
pois
t
unif
weibull
wilcox
Argument
shape1, shape2, ncp
size, prob
location, scale
df, ncp
rate
df1, df2, ncp
shape, scale
prob
m, n, k
meanlog, sdlog
location, scale
nbinom size, prob
mean, sd
lambda
df, ncp
min, max
shape, scale
m, n
Die obigen Befehlsnamen werden mit verschiedenen Präfixa versehen und können dann verwendet werden,
um verschiedene Aspekte der angegebenen Verteilungen abzubilden. Verwendet man zB ein p als Präfix, so
erhält man die Verteilungsfunktion. Verwendet man die angegebenen Funktionsnamen mit einem q davor,
so errechnet R den Wert der Quantilsfunktion (also der inversen Verteilungsfunktion). Mit dem Prefix
r erhält man Realisierungen aus Pseudo-Zufallsvariablen, die der entsprechenden Verteilung folgen, mit
dem Präfix d die Dichtefunktion. Die übergebenen Parameter entsprechen durchgängig den Parametern,
die die üblicherweise verwendet werden um die jeweiligen Verteilungsfamilien zu parametrisieren. Der
Parameter ncp kann dazu verwendet werden, nicht zentrierte Versionen von Verteilungen zu erhalten, die
normalerweise nur in zentrierter Form Anwendung finden (zB die χ2 oder F Verteilungen).
> (x <- pnorm(0.75, mean = 2, sd = 3))
[1] 0.3384611
> qnorm(x, mean = 2, sd = 3)
[1] 0.75
> hazard <- function(t, df) { return -pt(t, df, log = T, lower.tail=F) }
Die letzte Zeile im obigen Beispiel definiert die integrierte Hazardfuktion der t-Verteilung mit df Freiheitsgraden. Die dafür verwendeten Parameter sind log, welcher bestimmt, ob das Ergebnis logarthmiert
1
werden soll oder nicht und lower.tail welches bestimmt, ob P (X ≤ t) (im Falle von TRUE ) oder P (X > t)
berechnet werden soll.
2
Grafische Analyse
In der Statistik ist man oft mit der Aufgabe konfrontiert, ein Wahrscheinlichkeitsmodel für eine bestimmte
Zufallsvariable zu finden. Im einfachsten Fall besteht dieses Model aus einer Verteilung, aus der die Daten
’gezogen’ werden. Die Verteilungen sind meist a priori nicht gegeben und auch wenn theoretische Resultate
wie diverse Grenzwertsätze Hinweise geben, braucht es in der Praxis oft ein wenig Fingerspitzengefühl,
um tatsächlich eine passende Verteilung zu finden.
Die gängigen Hilfsmittel, um grundsätzlich eine passende Klasse von Verteilungen zu identifizieren sind
hierbei üblicherweise Grafiken, die die Charakteristiken der Verteilung in der einen oder anderen Weise
visualisieren. Es kommen hierbei - wie schon in der letzten Einheit besprochen - Histogramme, qq-Plots
usw zum Einsatz.
Im folgenden wird exemplarisch ein Anwendungsbeispiel durchgegangen in dem die Eruptionen eines
Geysirs analysiert werden. Die Daten sind in R vorhanden und werden mit attach geladen. Das DataFrame faithful weist unter anderem eine Variable eruptions auf, die der Gegenstand der Untersuchung
sein wird.
>
>
>
>
>
>
attach(faithful)
hist(eruptions, 20, freq
lines(density(eruptions,
lines(density(eruptions,
lines(density(eruptions,
rug(eruptions)
= F)
bw =0.01), col = ’’blue’’)
bw =0.1), col = ’’red’’)
bw =0.5), col = ’’green’’)
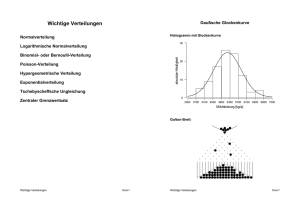
Ergebnis der obigen Codesequenz ist ein Histogramm auf dem zusätzlich unterschiedliche Dichteschätzer
mittels der Funktion density(. . . ) eingefügt wurden. Zu beachten ist hierbei der smoothness Parameter
bw, der mit zunehmender Höhe einen immer glatteren Schätzer bewirkt. Der Befehl rug() fügt eine Leiste
in das Diagramm ein, die die tatsächlichen Positionen der Datenpunkte ersichtlich macht.
Die erstellte Grafik, die hier in Abbildung 1 zu sehen ist, zeigt, dass die Daten in ihrer Gesamtheit keiner
der Standardverteilungen folgt. Insbesondere ist hier die Bimodalität auffällig. Eine weiterer interessanter
Plot zeigt die empirische Verteilungsfunktion, die man mit der Funktion ecdf(. . . ) leicht abfragen kann.
> plot(ecdf(eruptions), do.points=F, verticals=T)
Um die Analyse im letzten Beispiel zu vereinfachen schränkt man sich auf den zweiten ’Gipfel’ der
Verteilung ein und betrachtet nur die Datenpunkte größer drei. Die Hypothese ist, dass der gewählte
’Ausschnitt’ der Verteilung einer Normalverteilung entspricht.
2
0.6
0.3
0.0
Density
Histogram of eruptions
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
eruptions
0.4
0.0
Fn(x)
0.8
ecdf(eruptions)
2
3
4
5
x
Abbildung 1: Eine erste Analyse der Eruptionsdaten aus faithful
>
>
>
>
>
>
>
>
>
>
par(mfrow=c(2,1))
par(pty=’’s’’)
long <- eruptions[eruptions > 3]
plot(ecdf(long), do.points=FALSE, verticals=TRUE)
x <- seq(3, 5.4, 0.01)
lines(x, pnorm(x, mean=mean(long), sd=sqrt(var(long))), lty=2, lwd=2, col = ’’blue’’)
qqnorm(long)
qqline(long)
Die beiden Grafiken in Abbildung 2 deuten darauf hin, dass die Daten in etwa einer Normalverteilung
entsprechen könnten, jedoch das linke Ende der Verteilung etwas leichter ist als theoretischen Quantile
3
Normal Q−Q Plot
5.0
1.0
ecdf(long)
0.2
4.0
3.0
0.0
3.0
3.5
4.0
4.5
5.0
●
●
●
−2
x
●
●
●
●
●
●●
●●
●
●
●
● ●●
3.5
0.4
Fn(x)
0.6
Sample Quantiles
4.5
0.8
●
●●●
●●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
−1
0
1
2
Theoretical Quantiles
Abbildung 2: Der zweite Gipfel von der Verteilung von eruptions gegen die Nortmalverteilungsfunktion
bzw die entsprechenden Quantile
der Normalverteilung.
3
Anpassungstests
Ist man in der Analyse so weit, dass man eine ’Kanditatenverteilung’ gefunden hat, so kann man statistische
Tests of goodness of fit durchführen. In unserem Fall wären das Tests auf die Normalverteilung. Zwei Tests
die in R implementiert sind, sind zB der Shapiro-Wilk Test und der Kolmogorov-Smirnov Test. Beide
Testverfahren haben die Normalität (bzw beim K-S Test die Übereinstimmung der beiden Verteilungen)
als Nullhypothese. Ist diese gegeben der Daten unwahrscheinlich ist der p-Wert klein.
> shapiro.test(long)
Shapiro-Wilk normality
data: long
W = 0.9793, p-value = 0.01052
> ks.test(long, ’’pnorm’’, mean = mean(long), sd = sqrt(var(long)))
One-sample Kolmogorov-Smirnov test
data: long
D = 0.0661, p-value = 0.4284
alternative hypothesis: two.sided
Der Kolmogrov-Smirnov Test testet eigentlich die Übereinstimmung zweier beliebiger Verteilungen,
durch die Übergabe des Parameters ”pnorm” kann die Funktion allerdings auch mit nur einem Sample
verwendet werden (die Quantile der Normalverteilung werden in diesem Fall automatisch von R berechnet).
Weitere Optionen ermöglichen es einzustellen, ob die Hypothese einseitig oder zweiseitig getestet werden
soll. Die beiden Tests widersprechen sich insofern, als das der Shapiro-Wilk Test die Nullhypothese klar
ablehnt, während der Kolmogorov-Smirnov Test mit einem p-Wert von 0.4284 diesen Schluss nicht zulässt.
Es ist hierbei zu bemerken, dass es beim K-S Test theoretisch nicht korrekt ist, den Mittelwert und die
4
Varianz aus den Daten zu schätzen, gegen die man testet. Die Verteilung wird in diesem Fall zu stark
an die empirische Verteilung angepasst und der Test verliert an Macht. Eine Abhilfe verschafft hier der
sogenannte Lillifors-Test, der im wesentlichen den K-S-Test für den Normalverteilungsfall so adaptiert,
dass der Mittelwert und die Varianz aus den Daten geschätzt werden können.
> lillie.test(long)
Lilliefors (Kolmogorov-Smirnov) normality test
data: long
D = 0.0661, p-value = 0.05957
Die Korrektur bewirkt hier, dass die Nullhypothese nun ca auf einem 6% Niveau abgelehnt werden
kann. Die Daten können also in diesem Fall nicht als Normalverteilt angenommen werden. In einer weiterführenden Analyse würde man vielleicht die Anpassung einer t-Verteilung an die Daten ausprobieren.
Dies wird hier aber nicht mehr weiter verfolgt.
Andere Normalverteilungstests wären der Anderson-Darling-Test (ad.test(nortest)) oder der JargeBera-Test (jarque.bera.test(. . . )).
4
Maximum Likelihood
Ist man durch diverse Tests und Grafiken zur Auffassung gelangt, dass der daten generierende Prozess
einer bestimmten Verteilung folgt, so stellt sich die Frage, welche der Verteilungen in der entsprechenden
Familie die Daten am besten repräsentiert. Die Parameter der Verteilung müssen also geschätzt werden. Ein gängiges und universal anwendbares Schätzverfahren ist die Maximum Likelihood Methode. In
R ist die Maximum Likelihood Methode in Form der Funktion fitdistr(x, densfun, start, ...) (im Paket
MASS, welches zuerst geladen werden muss) implementiert. Hierbei wird mit dem Parameter densfun die
Verteilungsfamilie angegeben, für die die Parameter geschätzt werden sollen. Es stehen hierbei im Wesentlichen die Standardverteilungen für eindimensionale Zufallsvariablen zur Verfügung (Normalverteilung,
t-Verteilung, Chauchy-Verteilung, Exponentialverteilung, χ2 -Verteilung, . . . ). Da es sich bei der Maximum Likelihood Schätzung um ein Optimierungsproblem handelt, besteht die Schwierigkeit im Finden
eines passenden Schätzers hauptsächlich darin das Optimum der Likelihood Funktion zu finden. Um diese
Aufgabe für den solver einfacher zu gestalten, können mittels des Parameters start Anfangswerte für die
Optimierungsroutinen übergeben werden. Dies könnten zB Stichprobenmomente oder Schätzer, die aus
der Momentenmethode gewonnen werden, sein.
Ist das Model für das ein Maximum Likelihood Schätzer gefunden werden soll kein Standardverteilungsmodel - dies ist zB bei multidimensionalen Daten oder etwa Zeitreihenmodellen der Fall - dann kann
die Methode mle(. . . ) verwendet werden. Der grundlegende Unterschied zu fitdistr besteht hierbei darin,
dass die log likelihood Funktion als Argument übergeben werden muss.
5
Beispiele
1. Löse folgende Aufgabe mit R ohne die in Statistikeinführungen übliche Standardisierung der Normalverteilung durchzuführen und ohne auf die entsprechenden Testfunktionen in R zurückzugreifen:
The results of IQ tests are known to be normally distributed. Suppose that in 2002, the distribution of
IQ test scores for persons aged 18-35 years has a variance σ 2 = 225. A random sample of 9 persons
take the IQ test. The sample mean score is 115.
5
(a) Calculate the 50%, 75%, 90% and 95% confidence interval estimates of the unknown population
mean IQ score.
(b) If it is known that the population mean IQ score is µ = 105, what proportion of samples of size
6 will result in sample mean values in the interval [135,150]?
(c) Calculate the confidence intervals in (a) assuming the the Variance is not known and the sample
estimate isσ̂ 2 = 225.
2. Zeichne die Verteilung und die Konfidenzintervalle in 1(a). Verwende die Funktion abline(. . . ), um
die Grenzen der Konfidenzintervalle in verschiedenen Farben zu markieren.
3. In einer repräsentativen Umfrage für ein Land wurde das monatliche Einkommen von 240 Männern
und 160 Frauen erhoben. Das durchschnittliche Einkommen der Männer lag in der Stichprobe bei
1650 EUR, jenes der Frauen bei 1280 EUR. Die Standardabweichung des Einkommen betrug 270
EUR bei den Männern und 480 EUR bei den Frauen. Führe mittels R einen Test auf Varianzhomogenität durch und zeichne die entsprechende Verteilung und den Annahmebereich analog zu Beispiel
2.
4. (a) Schreibe eine Funktion, die die mittelere Augenzahl aus n Würfen mit einem 6-seitigen Würfel
zurückgibt.
(b) Verwende die Funktion aus (a), um eine Stichprobe von 3, 10, 100, 1000 solchen Mittelwerten
zu erlangen (n=10) und stelle die jeweiligen empirischen Verteilungen grafisch dar.
(c) Finde eine Verteilung, die gemessene empirische Verteilung mit 1000 Punkten beschreibt, und
belege Deine Wahl mit passenden Grafiken und Tests.
5. Lade das Datenfile Session5BSP5.R von der Homepage herunter. Teste die Daten auf Normalität
und finde durch grafische Analyse der Daten ein passendes Verteilungsmodel.
6. Schätze die Parameter der Verteilung aus 5 mittels der Maximum Likelihood Methode.
6