Wichtige Verteilungen

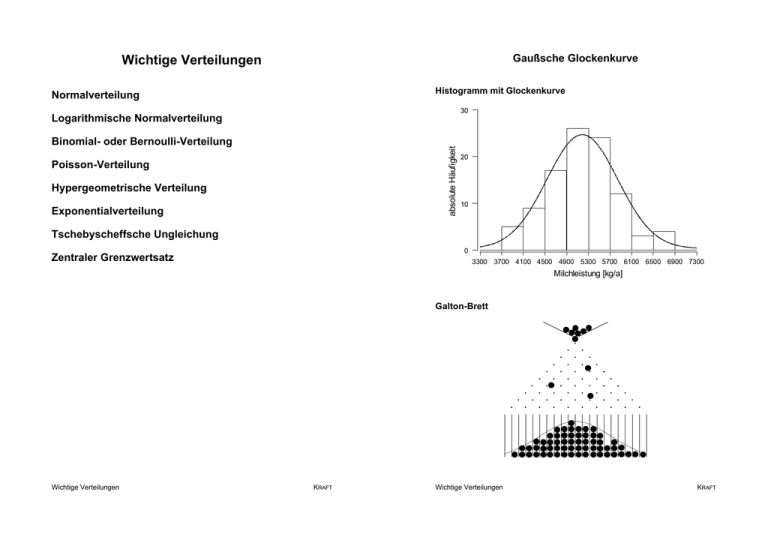
Gaußsche Glockenkurve
Wichtige Verteilungen
Histogramm mit Glockenkurve
Normalverteilung
30
Logarithmische Normalverteilung
absolute Häufigkeit
Binomial- oder Bernoulli-Verteilung
Poisson-Verteilung
Hypergeometrische Verteilung
Exponentialverteilung
20
10
Tschebyscheffsche Ungleichung
0
Zentraler Grenzwertsatz
3300 3700 4100 4500 4900 5300 5700 6100 6500 6900 7300
Milchleistung [kg/a]
Galton-Brett
Wichtige Verteilungen
KRAFT
Wichtige Verteilungen
KRAFT
Normalverteilung
Standardnormalverteilung
Dichtefunktion
&
1
f(x) '
F 2B
µ = E(X) = 0
F2 = Var(X) = 1
(x&µ)2
2F2
@e
für &4< x< %4 und F >0
Dichtefunktion
n(x) '
Verteilungsfunktion
F(x) '
x
&
@ e
m
F 2B &4
1
dt
0.5
F = 0.7
M(x) '
F=1
0.2
0.1
0.1
-3
0.0
-3
-2
-1
0
Wendepunkt
Wichtige Verteilungen
t2
2
dt
M(x)
1
: -2F
1
2
3
-2
-1
0.5
0
1
2
3 x
-3
-2
-1
0
1
2
3 x
x
Wendepunkt
F
: -3F
&
0.3
0.2
-4
x
@ e
m
2B &4
1
0.4
:=1
: = -2
0.3
-5
für &4 <x <%4
n(x)
:=0
F = 1.5
0.4
@e
x2
2
Verteilungsfunktion
µ = E(X):
Erwartungswert oder Mittelwert
F2 = Var(X): Varianz
f(x)
0.6
&
2B
(t&µ)2
2F2
1
: -F
F
:
: + F : +2 F : +3F
x
KRAFT
Wichtige Verteilungen
KRAFT
Spezielle Fraktilen und Grenzen
der Normalverteilung
Transformation auf Standardnormalvariable
X - (µ,F2)-n.v., dann ist
F(x) ' M
X&µ
- (0,12)-n.v.
F
x& µ
F
P(a<X#b) ' F(b)& F(a) ' M
b&µ
a&µ
&M
F
F
F
F
: -3F
: -2F
: -F
:
-3
-2
-1
0
1
2
u
3
M(!x)
M(x)
M(x)!M(!x)
0.000
1.000
1.645
1.960
2.000
2.326
2.576
3.000
3.090
3.290
4.000
0.5000
0.1587
0.0500
0.0250
0.0228
0.0100
0.0050
0.0013
0.0010
0.0005
0.5000
0.8413
0.9500
0.9750
0.9773
0.9900
0.9950
0.9987
0.9990
0.9995
0.0000
0.6826
0.9000
0.9500
0.9545
0.9800
0.9900
0.9974
0.9980
0.9990
0.9999
1F-Bereich: P(µ!1F<X#µ+0F) = M(1)!M(!1) = 0.6826 . 068%
2F-Bereich: P(µ!2F<X#µ+2F) = M(2)!M(!2) = 0.9545 . 095%
3F-Bereich: P(µ!3F<X#µ+3F) = M(3)!M(!3) = 0.9974 > 099%
4F-Bereich: P(µ!4F<X#µ+4F) = M(4)!M(!4) = 0.9999 . 100%
x
: + F : +2F : +3 F
x
P(µ!1.960F<X#µ+1.960F) = 0.950 = 95.0%
P(µ!2.576F<X#µ+2.576F) = 0.990 = 99.0%
P(µ!3.290F<X#µ+3.290F) = 0.999 = 99.9%
Additionstheorem der Normalverteilung
Die Summe von n unabhängigen normalverteilten Zufallsvariablen ist
wieder eine normalverteilte Zufallsvariable:
Xi (i = 1,2,...,n) - (µi Fi )-n.v., dann ist
X' j ki @ Xi - (µ F2)-n.v. mit µ ' j ki @ µi und F2 ' j ki @Fi
n
n
n
i'1
i'1
i'1
Wichtige Verteilungen
2
68%
16%
: -F
2
2
KRAFT
16%
: :+ F
Wichtige Verteilungen
2.5%
x
: -1.96 F
95%
:
2.5%
: +1.96 F
x
KRAFT
Milchleistung
M - (5000,6002)-n.v.
Logarithmische Normalverteilung
0.0007
X logarithmisch normalverteilt, wenn Y = log X normalverteilt
Y = log X - (log>,F2)-n.v.
0.0006
Dichte
0.0005
Dichte- und Verteilungsfunktion
0.0004
0.0003
log e
0.0002
f(x) '
0.0001
Fx 2B
&
(logx&log>)2
2F2
@e
für x >0
0
0.0000
3000
4000
5000
6000
für x# 0
7000
Milchleistung [kg/a]
2
F(x) '
1F-Bereich: P(µ!1F#M#µ+0F)=P(4400#M#5600).68%
2F-Bereich: P(µ!2F#M#µ+2F)=P(3800#M#6200).95%
3F-Bereich: P(µ!3F#M#µ+3F)=P(3200#M#6800).99%
logx & (t&log>)
2F2
@ e
m
F 2B &4
1
dt
0
P(µ!1.960F#M#µ+1.960F)=P(3824#M#6176)=95.0%
P(µ!2.576F#M#µ+2.576F)=P(3454#M#6546)=99.0%
P(µ!3.290F#M#µ+3.290F)=P(3026#M#6974)=99.9%
für x >0
für x# 0
1.0
F(x)
0.9
0.8
P(M=6000)=0
P(M<5000)=P(M#5000)=P(M>5000)=P(M$5000)=0.5
P(M<6000)=F(6000)=M((6000!5000)/600)=M(1.67)=0.9525
P(M>6200)=1!F(6200)=1!M(2)=1!0.9773=0.0227
P(5000#M#6000)=F(6000)!F(5000)=0.9525!0.5=0.4525
f(x), F(x)
0.7
0.6
0.5
0.4
0.3
P(M#c)=0.9]F(c)=M((c!5000)/600)=0.9]
](c!5000)/600=u0.95=1.282]c=5769
also P(M#5769)=90% und P(M>5769)=1-0.9=0.1=10%
P(µ!c#M#µ+c)=0.9]F(µ+c)!F(µ!c)=0.9]
] M((µ+c!µ)/F)!M((µ!c!µ)/F)=M(c/F)!M(!c/F)=0.9]
]c/F=80.9=1.645Yc=1.645@600=987
also P(4013#M#5987)=90%
Wichtige Verteilungen
0.2
0.1
f(x)
0.0
0
1
2
3
4
5
6
7
8
9
10
x
KRAFT
Wichtige Verteilungen
KRAFT
Hydroxymethylfurfurolgehalt von Honig
Bernoullisches Zufallsexperiment
Descriptive Statistics
2 Komplementäre Ereignisse: A (Erfolg) und A (kein Erfolg) mit P(A) =
p und P( A ) = q = 1 ! p (also p + q = 1)
Variable: HMF
n-malige Durchführung eines Bernoullischen Zufallsexperiments liefert
Folge von n Ereignissen A oder A ,
Anderson-Darling Normality Test
A-Squared:
P-Value:
0
2
4
6
8
95% Confidence Interval for Mu
3.085
0.000
Mean
StDev
Variance
Skewness
Kurtosis
N
2.34312
1.64210
2.69648
1.73887
3.83100
80
Minimum
1st Quartile
Median
3rd Quartile
Maximum
0.27000
1.14000
1.87500
2.92250
9.41000
z.B. AAA A A A ... A A AA (n mal)
mit P(AAA A A A ... A A AA) = p@p@p@q@p@q@...@q@q@p@p
Reihenfolge egal
P(AA...A k mal und A A ... A n!k mal) = pk@qn!k
n
n!
Anordnungen mit Wahrscheinlichkeit pk@qn!k
'
k
(n&k)! @k!
95% Confidence Interval for Mu
1.97769
1.6
2.1
2.6
2.70856
95% Confidence Interval for Sigma
1.42116
1.94502
95% Confidence Interval for Median
95% Confidence Interval for Median
1.61115
P(n,k,p) '
2.41885
Descriptive Statistics
n
k
@p k @ q n&k
(k' 0,1,2,...,n)
Münzwurf
Variable: ln HMF
p = q = 0.5
Anderson-Darling Normality Test
A-Squared:
P-Value:
-1.00
-0.25
0.50
1.25
2.00
95% Confidence Interval for Mu
0.180
0.913
Mean
StDev
Variance
Skewness
Kurtosis
N
0.637234
0.669219
0.447854
-1.4E-01
-4.7E-02
80
Minimum
1st Quartile
Median
3rd Quartile
Maximum
-1.30933
0.13103
0.62861
1.07243
2.24177
Urne: a rote, b grüne Kugeln, Ziehen mit Zurücklegen
p = a / (a + b), q = b / (a + b) = 1 ! p
Toxizitätsprüfung an Laborratten
Mortalitätsrate
Überlebensrate
95% Confidence Interval for Mu
0.48831
0.5
0.6
0.7
0.8
0.9
Wichtige Verteilungen
0.78616
p = 0.1 = 10%
q = 0.9 = 90% = 1 ! p
95% Confidence Interval for Sigma
0.57918
95% Confidence Interval for Median
(symmetrische Münze)
0.79267
95% Confidence Interval for Median
0.47689
0.88327
KRAFT
Wichtige Verteilungen
KRAFT
Bernoulli- oder Binomialverteilung
Toxizitätsprüfung
Wahrscheinlichkeits- und Verteilungsfunktion
P(n,x,p) '
f(x) '
n
x
@p x @(1 &p)n&x für x '0,1,2,ÿ,n
0
F(x) '
10 Ratten, Mortalitätsrate 10%
sonst
j f(t) für x$ 0
t#x
0
für x< 0
x
f(x) = P(X = x)
F(x) = P(X # x)
0
1
2
3
4
5
6
0.3487
0.3874
0.1937
0.0574
0.0112
0.0015
0.0001
0.3487
0.7361
0.9298
0.9872
0.9984
0.9999
1.0000
Erwartungswert und Varianz
10
@ 0.12 @ 0.98 ' 45@ 0.01@ 0.43' 0.19' 19%
2
P(#2) = F(2) = f(0) + f(1) + f(2) = 0.35 + 0.39 + 0.19 = 0.93 = 93%
P(<2) = f(0) + f(1) = F(1) = 0.35 + 0.39 = 0.74 = 74%
P(>2) = 1 ! P(#2) = 1 ! 0.93 = 0.07 = 7%
P($9) = P(9) + P(10) = 0.00 + 0.00 = 0
P(2) 'f(2) '
E(X) = n @ p, Var(X) = n @ p @ q
0.4
p = 0.1
n = 10
p = 0.9
p = 0.25
0.3
p = 0.75
f(x)
p = 0.5
1.0
0.9
0.2
0.8
f(x), F(x)
0.7
0.1
0.6
n = 10, p = 0.1
0.5
0.4
0.3
0.0
0
1
2
3
4
5
6
7
8
9
0.2
10
0.1
x
0.0
0
1
2
3
4
5
6
7
8
9
10
x
Wichtige Verteilungen
KRAFT
Wichtige Verteilungen
KRAFT
Poisson-Verteilung
Binomial- und Poisson-Verteilung
Wahrscheinlichkeits- und Verteilungsfunktion
Bernoulli-Experiment: n groß, p sehr klein (seltenes Ereignis)
Mit 8 = n@p Approximation der Binomial- durch Poisson-Vertlg.:
8k &8
P(n,k,p) ' P(k,8) .
@ e für n@p # 10 und n > 1500@p
k!
Beispiele:
P(x,8) '
f(x) '
8x &8
@ e für x' 0,1,2,ÿ
x!
0
Radioaktiver Zerfall ("-Teilchen pro Zeitintervall)
Druckfehler pro Seite
Fahrzeuge pro Zeitintervall
Unkrautsamen pro Flächeneinheit
Chromosomenaustausch in Zellen
F(x) '
e&8 @ j
t#x
sonst
8t
für x$ 0
t!
0
für x< 0
Erwartungswert und Varianz
E(X) = 8, Var(X) = 8
0.7
Binomial-, Poisson- und Normalverteilung
lambda = 0.5
0.6
0.5
Binomialverteilung mit E(X) = n @ p, Var(X) = n @ p @ q
f(x)
0.4
8 = n@p # 10 und n > 1500@p:
Poissonverteilung mit E(X) = 8, Var(X) = 8
0.3
8 $ 9:
Normalverteilung mit E(X) = µ = 8 und Var(X) = F2 = 8
lambda = 1
0.2
lambda = 4
0.1
0.0
0
1
2
3
4
5
6
7
8
9
10
11
12
x
Wichtige Verteilungen
KRAFT
Wichtige Verteilungen
KRAFT
Schadschwellenkonzept
Hypergeometrische Verteilung
Zufallsexperiment: Urne mit N Kugeln, davon N1 weiß und N2 = N ! N1
schwarz. Aus der Urne werden n Kugeln gezogen. Gesucht ist die
Wahrscheinlichkeit, genau k weiße zu ziehen.
Zählrahmen an 50 Stellen:
Problemunkräuter
Häufigkeit
0
1
2
3
4
5
6
06
15
12
13
02
01
01
6
6
mit Zurücklegen
ohne Zurücklegen
N
n
MUGE:
P
x '1.94, s 2 '1.69
'
N1 k
k
n&k
n&k
N
n
N1
Modell:
N n
Poisson-Modell mit 8 = 1.94
f(x) '
= P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) =
= e-1.94@(1.940/0!+1.941/1!+1.942/2!+1.943/3!+1.944/4!) =
= 0.1437 @ (1 + 1.94 + 1.8818 + 1.2169 + 0.5902) =
= 0.9526 = 95.25%
P
Wahrscheinlichkeit, daß mehr als 4 Unkräuter vorkommen, ist also
kleiner als 5%
KRAFT
N1 x
'
N&N1
@
x
n&x
für x' 0,1,2,ÿ,min(N1,n)
N
n
0
sonst
Erwartungswert und Varianz
= 1 ! P(X # 4) = 1 ! 0.9526 = 0.0474 = 4.74%
Wichtige Verteilungen
N&N1
Wahrscheinlichkeitsfunktion
> 4 Unkräuter pro Zählrahmen
P(X > 4)
k
@
N&N1
@
Schadschwelle:
P(X # 4)
N1
GUGE:
N1
N n
Binomialverteilung
Hypergeometrische Verteilung
E(X)' n@
N1
N
, Var(X) 'n @
Wichtige Verteilungen
N1
N
@ 1&
N1
N
@
N&n
N&1
KRAFT
Biologiestudenten
Exponentialverteilung
20 Biologiestudenten, davon 15 weiblich (w) und 5 männlich (m), 10
Studenten zufällig ausgewählt
Dichte- und Verteilungsfunktion
Wahrscheinlichkeit nur weibliche:
f(x) '
P(10w)'
15
10
@
5
0
8 @e&8@ x für x $0, 8> 0
0
20
10
E(X)'
P(8w,2m)'
0
für x <0
Erwartungswert und Varianz
Wahrscheinlichkeit 8 weibliche und 2 männliche:
15
8
1 &8 @e&8@ x für x $0, 8> 0
F(x) '
' 0.016' 1.6%
für x <0
@
5
2
1
1
, Var(X)'
8
82
' 0.348' 34.8%
20
10
1.0
f(x)
F(x)
P(5w,5m)'
15
5
@
5
5
f(x), F(x)
Wahrscheinlichkeit 5 weibliche und 5 männliche:
' 0.016' 1.6%
20
10
0.5
8=1
0.0
0
1
2
3
4
5
x
Wichtige Verteilungen
KRAFT
Wichtige Verteilungen
KRAFT
Tschernobyl
137
55
Cs 6
137
56
Ba +
0
&1
e,
Tschebyscheffsche Ungleichung
X beliebig verteilt mit E(X) = µ und Var(X) = F2 … 0, dann gilt:
tH = 30 a
Lebensdauer T (Zeit bis zum Zerfall) eines Cäsiumkerns ist exponentialverteilt nach f(t) = 8 @ e!8 @ t bzw. F(t) = 1 ! e!8t
P(|X ! µ| < k@F) $ 1 ! 1/k2 oder P(|X ! µ| $ k@F) # 1/k2
Halbwertszeit = Median: tH = t0.5 = 30 a
Zerfallskonstante 8: F(tH) = 0.5 = 1 ! e!8 @ 30 a, also 8 = 0.023 a!1
Erwartungswert: E(T) = 1/8 = 43 a
P(|X!µ|<2F) = 0.75 = 75% oder P(|X!µ|$2F) = 0.25 = 25%
P(|X!µ|<3F) = 0.89 = 89% oder P(|X!µ|$3F) = 0.11 = 11%
P(|X!µ|<4F) = 0.94 = 94% oder P(|X!µ|$4F) = 0.06 = 06%
Wahrscheinlichkeit, daß Cäsiumkern höchstens 30 a überlebt:
P(T # 30 a) = 50% = 0.5 = F(30 a) = 1 ! e!0.023 1/a @ 30 a
Wahrscheinlichkeit, daß Cäsiumkern höchstens 43 a überlebt:
P(T # 43 a) = F(43 a) = 1 ! e!0.023 1/a @ 43 a = 1 ! 0.37 = 0.63 = 63%
Bei einer beliebigen Verteilung liegen also mindestens 75% aller möglichen Realisationen innerhalb des 2F-Bereichs, 89% innerhalb des 3FBereichs und 94% innerhalb des 4F-Bereichs. Oder anders herum:
Höchstens 25% liegen außerhalb des 2F-Bereichs, 11% außerhalb des
3F-Bereichs und 6% außerhalb des 4F-Bereichs.
Wahrscheinlichkeit, daß Cäsiumkern mindestens 100 a überlebt:
P(T $ 100 a) = 1 ! F(100 a) = e!0.023 1/a @ 100 a = 0.10 = 10%
Für spezielle Verteilungen kann man natürlich schärfere Aussagen
formulieren, z.B. für die Normalverteilung:
P(|X!µ| $ 2F) = 0.0455
P(|X!µ| $ 3F) = 0.0027
P(|X!µ| $ 4F) = 0.0000
1.0
0.9
0.8
0.7
F(t)
0.6
0.5
Zentraler Grenzwertsatz
0.4
0.3
Xi (i = 1,2,...,n) mit E(Xi) = µi und Var(Xi) = Fi2 beliebig verteilt
0.2
X' j Xi - (nµ,nF2)-n.v. für n 6 4 (praktisch für n relativ groß)
n
0.1
i'1
0.0
0
10
20
30
40
50
60
70
80
90
100
t [a]
Wichtige Verteilungen
KRAFT
Wichtige Verteilungen
KRAFT