GEM Übung SS 2016
Werbung

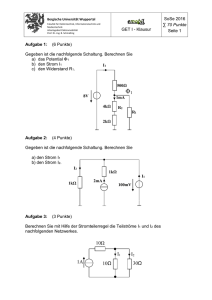
GEM Übung SS GEM Übung SS 2016 / GEM Übung SS / Übung 1: Einheiten und Messunsicherheit 1.1 Aufgabe 1 Aufgabe Messunsicherheit Die Messung einer Spannung U, die mit zufälligen normalverteilten Messunsicherheiten behaftet ist, ergab unterschiedliche Messwerte: Messung Nr. U /mV 1 995 2 993 3 4 5 1006 994 1003 Tabelle .: Messwerte 6 1001 7 1005 8 999 (a) Durch welche Parameter ist eine Normalverteilung gekennzeichnet? (b) Wie groß sind der Schätzwert des Mittelwertes und die Standardabweichung der Einzelwerte? (c) Zeichnen Sie mit den ermittelten Parametern den Verlauf der Dichtefunktion, wie sie für große Messreihen gültig wäre. (d) In welchem Intervall ∆U sind 68, 3% bzw. 99, 7% aller Einzelwerte zu erwarten? GEM Übung SS / Übung 2: Wechselstromgrößen 2.1 Aufgabe 2 Aufgabe Komplexe Messgrößen, Zeigerdiagramm Die Messschaltung in Abbildung . besteht aus einer Spannungsquelle, einem ohmschen Spannungsteiler und einer unbekannten komplexen Lastimpedanz ZX . Die Last soll bestimmt werden. Dazu wurden die Spannungen UT und U0 auf einem Oszilloskop dargestellt. Die Bildschirmdarstellung mit den nachfolgenden Einstellungen und Werten zeigt Abbildung .. R: 1 kΩ R: 1 kΩ Kanal : U0 1 V/ DIV Kanal : UT 1 V/ DIV Zeitbasis: 500 ns/ DIV IR UR 1 1 R1 UT IR R2 U0 2 IX Z ZX Abbildung .: Schaltung Ch1: U0 (a) Welche Frequenzen und welche Scheitelwerte haben die beiden Signale? (b) Ist die Last ZX induktiv oder kapazitiv? Begründen Sie anhand eines Zeigerdiagramms. Ch2: UT (c) Berechnen Sie allgemein den Phasor der Spannung UT . Rechnen Sie hierfür mit der komplexen Impedanz ZX . (d) Berechnen Sie die (komplexe) Impedanz ZX zunächst allgemein (U0 und UT seien bekannt) und geben Sie deren Wert an. (e) Zeichnen Sie ein Ersatzschaltbild, welches den in (d) berechneten Impedanzwert von ZX bei der betrachteten Frequenz realisiert. Berechnen Sie die Werte der Komponenten des Ersatzschaltbildes. Abbildung .: Oszilloskopbild GEM Übung SS / Übung 3: Statistik, Messunsicherheit 3.1 Aufgabe 3 Aufgabe Statistik Durch die gleichzeitige Messung von Strom und Spannung soll der Widerstand R bestimmt werden. Abbildung .: Messschaltung Der Innenwiderstand des Amperemeters beträgt RA = 100 mΩ und der des Voltmeters RV = 2 MΩ. Folgende Werte wurden durch neun aufeinanderfolgende Einzelmessungen ermittelt. (Annahme: Messwerte folgen einer Gaußverteilung) Messung Nr. U /V I/mA 1 12,4 243 2 12,1 238 3 4 5 11,4 12,6 11,9 238 243 239 Tabelle .: Messwerte 6 12,2 244 7 11,7 241 8 12,3 244 9 11,8 239 (a) Wie groß sind die Mittelwerte der Spannungs- und Strommessung? (b) Wie groß sind die empirischen Standardabweichungen der Messungen? (c) Berechnen Sie den Wert des Widerstandes aus den Mittelwerten der Strom- und Spannungsmessung. (d) Ermitteln Sie die empirische Standardabweichung des Widerstandes mit Hilfe des Gauß’schen Fehlerfortpflanzungsgesetzes. (e) Geben Sie die Messunsicherheit der Widerstandsmessung basierend auf neun Messwerten für einen Vertrauensbereich von % an! (Studentfaktor t=,) (f ) Geben Sie das vollständige Messergebnis für den Widerstand an. (g) Die Messschaltung enthält einen systematischen Fehler, welchen? (h) Welcher Widerstandswert ergibt sich unter Berücksichtigung des systematischen Fehlers? / GEM Übung SS Statistik, Messunsicherheit 3.2 Aufgabe 4 Aufgabe Regression Für einen Widerstand wurden die folgenden Strom-Spannungspaare aufgenommen: U/V 1 2 2,5 4 5 I / mA U/V I / mA 11,7 7 81 23,1 8 92 28,75 8,5 97 45,5 9 103,5 57,5 9,5 109,8 Tabelle .: Messwerte (a) Zeichnen Sie den Graphen I (U ). (b) Berechnen Sie die Regressionsgerade für den Strom als Funktion der Spannung. (c) Ergänzen Sie die Regressionsgerade in den Graphen aus Punkt (a). GEM Übung SS . Aufg. / 3.3 Aufgabe 5 Aufgabe Statistik Bei der Produktion von Dünnfilmwiderständen mit Nominalwert 1 kΩ wird durch den Hersteller bei einer Stichprobe von Widerständen durch eine Strom- und Spannungsmessung der Widerstandswert bestimmt. Tabelle . zeigt die Ergebnisse der Messungen. Nehmen Sie an, dass die Werte einer Gaußverteilung unterliegen. Wertebereich / Ω 964 ± 6 Anzahl der Widerstän de im Wertebereich 976 ± 6 988 ± 6 1000 ± 6 1012 ± 6 1024 ± 6 1036 ± 6 Tabelle .: Messwerte (a) Diskutieren Sie kurz, mit Begründung, ob es sich bei diesen Abweichungen um einen systematischen oder um einen zufälligen Fehler handelt. (b) Wie groß sind der empirische Mittelwert µR und die empirische Standardabweichung sR ? (c) Wie viele Widerstände können unter Annahme der Gaußverteilung mit der Toleranzangabe von 1 % versehen werden? Hinweis: Berechnen Sie zunächst die Intervallgrenzen und geben Sie den Abstand vom Mittelwert an. (d) Zwei Widerstände R1 und R2 aus obiger Produktion, welche in der Toleranzklasse % liegen werden zu einem Spannungsteiler (vgl. Abbildung .) mit der Speisespannung U0 verbaut. Die Ausgangsspannung U1 , welche als Referenz für ein Messgerät dient, weicht dementsprechend vom Sollwert ab. Handelt es sich bei der resultierenden Abweichung des Messergebnisses um einen zufälligen oder systematischen Fehler? Begründen Sie kurz. R2 U0 R1 U1 Abbildung .: Spannungsteiler (e) Berechnen Sie die maximale Abweichung der Ausgangsspannung U1 des Spannungsteilers, welche sich auf Grund der Toleranzen ergibt mittels des passenden Fehlerfortpflanzungsgesetzes zunächst allgemein und dann als Zahlenwert für U0 = 5 V. Hinweis: Bedenken Sie, dass durch die Selektion die Verteilung aus Punkt (c) nicht mehr gilt. GEM Übung SS / Übung 4: Signalkenngrößen 4.1 Aufgabe 6 Aufgabe Formfaktor, Crestfaktor Das periodische Signal hat dreieckförmige Abschnitte mit einem Scheitelwert von US = 20 V. Die Dioden D bis D sind als ideal anzunehmen (Spannung in Durchlassrichtung UF = 0 V). U1/US D1 1 0 600 1200 t/µs D3 U1 -1 Umess R D2 D4 Abbildung .: Messspannung und Messaufbau (a) Bestimmen Sie die Frequenz und die Periodendauer des angegebenen Spannungsverlaufs. (b) Skizzieren Sie den zeitlichen Verlauf der Spannung Umess an dem Spannungsmessgerät. (c) Bestimmen Sie den Scheitelfaktor von Umess allgemein. (d) Bestimmen Sie den Formfaktor von Umess allgemein. (e) Berechnen Sie die Spannung, die ein Drehspulmesswerk anzeigen würde. / GEM Übung SS Signalkenngrößen 4.2 Aufgabe 7 Aufgabe Formfaktor, Crestfaktor Das periodische Signal hat sinusförmige Abschnitte und wechselt im Maximum das Vorzeichen. 1 i / I0 0.5 0 −0.5 −1 0 20 40 60 80 100 t / ms 120 140 160 Abbildung .: Zeitsignal Z T = 2π ω 0 sin2 (ω t) dt = π ω (a) Berechnen Sie die Frequenz und die Periodendauer des angegebenen Signalverlaufs. (b) Berechnen Sie den Mittelwert des Signals. (c) Berechnen Sie den Scheitelfaktor des Signals. (d) Berechnen Sie den Formfaktor des Signals. (e) Berechnen Sie die Leistung, die in einem 50 Ω-Widerstand umgesetzt wird. (.) GEM Übung SS / Übung 5: Messschaltungen 5.1 Aufgabe 8 Aufgabe Z-Diode Eine Schaltung mit einer idealen Z-Diode 9 V / 2, 1 W zur Spannungsstabilisierung soll dimensioniert werden. Die Nenndaten der Lampe sind mit 9 V / 0, 2 W angegeben. Über den Schalter S1 kann ein Netzwerk zugeschaltet werden. In der Last RL soll bei 5 V eine Leistung von 33 mW umgesetzt werden. Gegeben ist R2 = 100 Ω. Die Eingangsspannung schwankt mit UE = 12V ± 10%. Abbildung .: Schaltungsaufbau (a) Wie groß sind die maximale und die minimale Eingangsspannung? (b) Dimensionieren Sie den Widerstand R3 . (c) Berechnen Sie den minimalen und den maximalen Strom I1 . (d) In welchem Bereich kann R1 dimensioniert werden? Es gilt IZmin = 10% · IZmax . (e) Zeichnen Sie für R1 = 20 Ω die Arbeitsgeraden und die Arbeitspunkte in die ideale Kennlinie ∧ der Z-Diode für die Eingangsgrenzen ein. Es gelte I1 = und UE = 12 V (Massstab: 10 V = ∧ 10 cm; 200 mA = 10 cm) (f ) Muss eine Z-Diode mit höherer Verlustleistung PV verwendet werden, wenn die Lampe durchbrennt? Es gilt: R1 = 20 Ω und S1 offen. (g) Skizzieren Sie die Kennlinie einer realen Z-Diode. GEM Übung SS / Übung 6: Messaufnehmer 6.1 Aufgabe 9 Aufgabe Differentialkondensator Ein Verfahren der Weglängenmessung beruht auf der Kapazitätsänderung eines Plattenkondensators. Die zu messende Strecke ∆s wird dabei direkt in einen veränderten Plattenabstand umgesetzt. Abbildung .: variabler Einzelkondensator Einzelkondensator Mit Hilfe einer Wechselstromquelle wird ein Strom mit einer Kreisfrequenz ω mit Amplitude I0 eingeprägt. (a) Berechnen Sie die über dem Kondensator abfallende Spannung UC allgemein bei einer Wegänderung um ∆s. Der Plattenfläche sei A, die Dielektrizitätskonstante 0 , die relative Permittivität r , der Plattenabstand im Ausgangszustand d. Hinweis: die Kapazität steigt mit größerer Plattenfläche A und sinkt mit größerem Abstand d! (b) Berechnen Sie die Empfindlichkeit E = ∂UC ∂ ∆s ! Differentialkondensator und Brückenschaltung Die Parameter des Kondensators können einer gewissen Streuung unterliegen. Deshalb werden häufig Differentialkondensatoren verwendet. Diese bestehen aus zwei Kondensatoren, die über eine gemeinsame Platte verbunden sind. Diese kann um den Weg ∆s verschoben werden. Abbildung .: Differentialkondensator Gehen Sie davon aus, dass beide Kondensatoren dasselbe A, r , und d im Ausgangszustand aufweisen. (c) Ihnen stehen zwei zusätzliche Widerstände R1 und R2 und eine Spannungsquelle mit Spannung U0 und Kreisfrequenz ω zur Verfügung. Wie kann gemeinsam mit dem Differentialkondensator eine Brücke erstellt werden? Um welche Arte von Brückenschaltung handelt es sich? (d) Berechnen Sie die Diagonalspannung UD der Brücke allgemein als Funktion von ∆s. Lösen Sie alle Doppelbrüche auf. / GEM Übung SS Messaufnehmer (e) Wie müssen die Widerstände R1 und R2 gewählt werden, damit die Brücke für ∆s = 0 abgeglichen ist? Berechnen Sie ihre Werte für eine Speisespannung von 15 V so, dass durch die Widerstände ein Strom von 20 mA fließt. (f ) Zeigen Sie, dass die Empfindlichkeit der Brücke E = ∂UD ∂ ∆s unabhängig von A, 0 und r ist. (g) Zeigen Sie, dass der Strom, der von der Quelle in die Brücke fließt, unabhängig von ∆s ist. (h) Zeichnen Sie das Zeigerdiagramm für den Zusammenhang zwischen Diagonalspannung und Speisespannung für eine Kreisfrequenz von 10 kHz bei einer Weglängenänderung von ∆s/d = 10%. Die Kapazitäten im Ausgangszustand seien C1 = C2 = 100 nF. Tragen Sie außerdem die Ströme ein. Der Maßstab sei 1 cm/V bzw. 1 cm/10 mA. GEM Übung SS / Übung 7: Messaufnehmer 7.1 Aufgabe 10 Aufgabe Temperatursensoren Widerstandsthermometer aus Halbleitern oder Metallen werden als Kontaktthermometer über einen großen Temperaturbereich eingesetzt. (a) Zeichnen Sie die Kennlinien R(T ) eines Si- und eines PT-Widerstandsthermometers. Zeichnen Sie in einem zweiten Diagramm die Empfindlichkeit E = |dR/dT |. In welchem Temperaturbereich wird welcher Sensortyp bevorzugt? Warum? (b) Wie ist die Formel für den Widerstand eines PT als Funktion der Temperatur? (c) Der PT wird mit einem Strom von 1 mA gespeist. Wie groß ist die in ihm umgesetzte Leistung bei einer Temperatur von 300 K? α sei 4 · 10−3 K−1 . Ein weiterer Temperatursensor ist das Thermoelement. (d) Skizzieren Sie den Aufbau eines Thermoelements. Wie ist die Formel für die Thermospannung? (e) Geben Sie drei systematische Fehler an, die bei der Temperaturmessung mit einem Kontaktthermometer auftreten können. Einige dieser Messfehler können durch die Verwendung eines Pyrometers vermieden werden. (f ) Wann werden Pyrometer eingesetzt? (g) Skizzieren Sie den Aufbau eines Pyrometers! Welche Strahlungsdetektoren kommen zum Einsatz? (h) Welches Gesetz beschreibt das Spektrum eines schwarzen Körpers? Skizzieren Sie Kurven für 300 K, 3000 K und 6000 K. Wie wird die Wellenlänge des Maximums der Kurve bestimmt? (i) Wird die Temperatur für einen grauen Körper, für den die Emission unbekannt ist, unterschätzt oder überschätzt wenn ein von angenommen wird? Warum? (j) Wie kann diese Abweichung behoben werden? / GEM Übung SS Messaufnehmer 7.2 Aufgabe 11 Aufgabe Temperatursensoren Zur Messung der Temperatur ϑm mit einem Thermoelement benötigt man eine konstante Vergleichstemperatur ϑv am Übergang vom Ausgleichsleiter zum Kupferleiter. Die Empfindlichkeiten der Thermoelemente sind für ϑv = °C tabelliert. Für das hier verwendete beträgt sie kAB = 3 mV/100 K bei 0 ◦ C. Weicht die Temperatur der Vergleichsstelle von 0 ◦ C ab, so wird die Messung verfälscht. Mit Hilfe einer Brückenschaltung mit Temperatursensoren, die die Vergleichstemperatur messen, lässt sich dieser systematische Fehler korrigieren. Abbildung .: Schaltungsaufbau Thermoelement (a) Wie groß ist die thermoelektrische Spannung Uth am Thermoelement aus den Materialien A und B, wenn es auf die Temperatur ϑm gebracht wird (Formel)? Die Referenztemperatur sei mit ϑv bezeichnet. Brückenschaltung Die Brücke bestehend aus zwei Pt-Temperatursensoren und zwei Festwiderständen wird mit der Spannung U0 gespeist. (b) Wie ist der Zusammenhang des Widerstandes RPt mit der Temperatur ϑv ? (c) Wie groß ist die Diagonalspannung UD als Funktion von R1 , R2 , RPt und U0 ? (d) Wie groß muss R1 = R2 = R gewählt werden, damit die Brücke bei ϑv = °C abgeglichen ist? (e) Wie groß ist die Diagonalspannung UD bei einer bei ϑv = °C abgeglichenen Brücke in Abhängigkeit von ϑv ? (Allgemeine Formel!) (f ) Geben Sie die Empfindlichkeit dUD /dϑv der Diagonalspannung bei ϑv = ◦ C an. Kompensation Der Temperaturkoeffizient der temperaturabhängigen Pt-Widerstände ist αPt = 4 · 10−3 K−1 . (g) Wie groß muss U0 gewählt werden, wenn die Empfindlichkeit des Thermoelements und die Empfindlichkeit der Brückenspannung dUD /dϑv (ϑv = 0 ◦ C) gleich sein sollen? GEM Übung SS / Übung 8: Messaufnehmer 8.1 Aufgabe 12 Aufgabe Brücke, Abgleich, Wechselstrombrücke Gegeben sei die abgebildete Brückenschaltung. Abbildung .: Brückenschaltung Die Widerstände R1 = R2 = R0 und die Speisespannung U0 sind nicht fehlerbehaftet. Die Widerstände R3 und R4 weisen jedoch bei einem Nennwert R3 = R4 = R0 folgende Toleranzen auf: ∆R3 /R3 = ±2% und ∆R4 /R4 = ±2%. Ferner gilt R0 = 10 kΩ sowie U0 = 50 V. (a) Bestimmen Sie die Diagonalspannung Um als Funktion von R1 , R2 , R3 , R4 und U0 . (b) Bestimmen Sie die Abgleichbedingung der Brücke. (c) Bestimmen Sie den absoluten Fehler ∆Um der Brückendiagonalspannung für die gemäß Toleranzen ungenauen Werte von R3 und R4 . Abbildung .: Wechselstrom-Brückenschaltungen (d) Welche der Messbrücken sind prinzipiell abgleichbar? GEM Übung SS / Übung 9: Messelektronik 9.1 Aufgabe 13 Aufgabe Operationsverstärker: Messverstärker für kleine Gleichspannungen Als Eingangsverstärker für Temperaturmessungen mit einem Thermoelement soll eine rauscharme Schaltung mit einem Operationsverstärker dimensioniert werden. (a) Zeichnen Sie die Schaltungen eines invertierenden und eines nicht-invertierenden Verstärkers mit einem Operationsverstärker. Geben Sie die Verstärkungsfaktoren beider Schaltungen allgemein an. (b) Dimensionieren Sie den Rückkopplungswiderstand des invertierenden Verstärkers aus Punkt (a) so, dass der Verstärkungsfaktor −5 beträgt. Der Eingangswiderstand der Schaltung soll einen Wert von 1 MΩ aufweisen. (c) Was für eine Funktion bekommt die Schaltung des invertierenden Verstärkers aus Punkt (b), wenn der größere der beiden Widerstände durch einen Kondensator mit einer Kapazität von 2 µF ersetzt wird? Welche Zeitkonstante weist die Schaltung auf und welche Bedeutung hat diese Zeitkonstante für die Funktion der Schaltung? Zeichnen Sie den Schaltplan und das Bode-Diagramm. (d) Berechnen Sie den Effektivwert des Spannungsrauschens des Eingangswiderstands von 1 MΩ bei einer Bandbreite von 10 Hz und einer Temperatur von T = 27 ◦ C. Die Boltzmann-Konstante ist kB = 1,381 · 10−23 J/K. Berechnen Sie den Wert der spektralen Rauschleistungsdichte SV . (e) Skizzieren Sie das Diagramm für die Abhängigkeit der gesamten spektralen Rauschleistungsdichte des Spannungsrauschens SV der Schaltung aus Punkt (b) von der Frequenz. Welche Beiträge zum Rauschen erwarten Sie? Beschreiben Sie die Abhängigkeit der Rauschbeiträge von der Frequenz. (f ) Der invertierende Verstärker soll nun durch einen zusätzlichen Widerstand zu einem Summierverstärker ergänzt werden. Dabei soll die Verstärkung für das zweite Eingangssignal halb so groß wie für das erste sein. Wie muss der zusätzliche Widerstand gewählt werden? (g) Welches effektive Stromrauschen wird von den beiden Eingangswiderständen erzeugt? Der nicht-invertierende Verstärker aus Punkt (a) besitzte eine Verstärkung von 10 und soll einen Eingangswiderstand von 1 MΩ aufweisen. (h) Wie könnte die Schaltung aus Aufgabenteil (a) ergänzt werden, um den gewünschten Eingangswiderstand zu erhalten? Welches effektive Spannungsrauschen wird in diesem Fall am Ausgang des Operationsverstärkers durch das zusätzliche Bauteil erzeugt? / GEM Übung SS Messelektronik 9.2 Aufgabe 14 Aufgabe Operationsverstärker: Messverstärker für kleine Gleichspannungen Es soll für einen invertierenden Verstärker eine Abgleichmöglichkeit für eine Offsetspannung vorgenommen werden. Die Offsetspannung wird am Potentiometer P abgeglichen. Die Betriebsspannung sei UB = ±15 V. Abbildung .: Schaltungsaufbau (a) Wie groß ist die Spannungsverstärkung für ein Signal am Eingang UE ? (b) Wie groß ist der Eingangswiderstand für ein Signal am Eingang UE ? (c) Es sei eine Verstärkung von UA /UE = −10 eingestellt. Dabei sei R1 = 100 kΩ. Wie groß ist der Strom im Widerstand R2 , der bei UE = 0 V durch eine Offsetspannung von UA = ±10 mV am Ausgang entsteht? (d) Dieser Offset-Strom durch R2 wird mit einem Strom durch den Spannungsteiler aus zwei Widerständen RV und das Potentiometer P kompensiert. Über den unbelasteten Spannungsteiler soll ein Querstrom von 10 µA fließen. Dimensionieren Sie die Vorwiderstände RV und das Potentiometer P so, dass durch Vollausschlag des Potentiometers P der Offset-Strom kompensiert werden kann. (e) Wie groß ist die Spektraldichte des Spannungsrauschens und des Stromrauschens durch den Widerstand R1 am invertierenden Eingang des Operationsverstärkers? Dabei ist mit kB = 1,381 · 10−23 J/K und T = 27 ◦ C zu rechnen. GEM Übung SS / Übung 10: ADC, DAC 10.1 Aufgabe 15 Aufgabe Digital-Analog-Umsetzer Die abgebildete Schaltung, bestehend aus Referenzspannungsquelle, Widerstandsnetzwerk, Schaltern und Operationsverstärker, soll zur Digital-Analog-Umsetzung verwendet werden. Abbildung .: DAC-Netzwerk (a) Wie sollten die Widerstände R1 . . . R8 dimensioniert werden? Geben Sie die Werte als Vielfache von R so an, dass die resultierenden Ströme entsprechend der eingestellten Binärzahl gestaffelt sind! Wie heißt dieser Umsetzer? (b) Geben Sie die Ströme und Spannungen über R1 , R3 , R5 , R7 als Funktion von R und Uref an. (c) Bestimmen Sie Ua für die gegebene Schalterstellung des -Bit-Umsetzers als Funktion von Uref , R und RN (d) Wie groß ist der Gesamtwiderstand des Netzwerkes als Lastwiderstand der Referenzquelle? Wie groß ist die Spektraldichte des weissen Stromrauschens dieses Gesamtwiderstands bei einer Temperatur von 27 ◦ C? Rechnen Sie mit kB = 1,381 · 10−23 J/K. (e) Es gelte RN = R = 1 kΩ. Wie groß darf der Innenwiderstand der Referenzquelle sein, damit der Fehler der Ausgangsspannung betragsmäßig kleiner als ein Inkrement bleibt? (f ) Bei welchem der Widerstände R1 . . . R8 wirken sich Widerstandstoleranzen besonders stark auf Ua aus, das heißt, welcher Widerstand im Netzwerk ist kritisch? (g) Welche Toleranz darf dieser Widerstand besitzen, damit Ua eine Unsicherheit von 0,5 Inkrementen einhält? / GEM Übung SS ADC, DAC 10.2 Aufgabe 16 Aufgabe Analog-Digital-Umsetzer Der in Abbildung . gezeigte Umsetzer soll für eine Taktfrequenz fT = 1 MHz des Zählers und einen Eingangsspannungsbereich von 0 V bis 2,5 V dimensioniert werden. Der Eingangsspannung ist eine 16 23 Hz–Störspannung (reine Wechselspannung) überlagert. S2 Cf Iin Uin Uref 1 2 S1 VS Rg Vn Vint A1 VK & K1 Z Zähler m Takt fT Reset Steuerung En Abbildung .: Schaltung des Analog-Digital-Umsetzers (a) Abbildung . zeigt eine Analog-Digital-Umsetzer-Schaltung. Benennen Sie den Typ dieses Umsetzers. Nennen mindestens drei weitere Typen von AD-Umsetzern. (b) Die zu messende Spannung darf mit maximal Iin = 10 µA belastet werden. Bestimmen Sie den passenden Widerstandswert Rg , damit dies genau erfüllt ist. (c) Wählen Sie die minimale Integrationszeit tint so, dass die der Eingangsspannung überlagerte Störspannung keine Auswirkungen auf das Ergebnis der AD-Umsetzung zeigt und begründen Sie kurz Ihre Wahl. (d) Die Ausgangsspannung am Integrator soll einen Wert Vint = −2V nicht unterschreiten. Bestimmen Sie den zugehörigen Kondensator Cf in Abhängigkeit von Rg und tint . (e) Wie groß muss die Referenzspannung Uref gewählt werden, um bei einer Eingangsspannung von Uin = 1 V einen Zählerstand von m = 24 · 103 zu erreichen? (f ) Skizzieren Sie den zeitlichen Verlauf der Eingangsspannung Uin = 0,5 V und der Integratorausgangsspannung Vint in einem Zeitdiagramm über eine Messperiode für die wie zuvor dimensionierte Schaltung. (g) Geben Sie die Formel zur Berechnung der Spannung Uin aus dem Zählerwert m allgemein an. (h) Wie wirkt sich eine Veränderung der Werte von Rg , Cf und fT (z. B. durch Alterung) auf die Genauigkeit aus? (i) Welches ist für den spezifizierten Spannungsbereich und mit den dimensionierten Werten die maximale Dauer eines A/D-Wandlungs-Zyklus? GEM Übung SS . Aufg. / (j) Welche maximale Frequenz darf die Eingangsspannung Uin aufweisen, damit das Eingangssignal noch korrekt erfasst wird? Was passiert bei höheren Eingangsfrequenzen? GEM Übung SS / Übung 11: Oszilloskop 11.1 Aufgabe 17 Aufgabe Tastkopf für ein Oszilloskop Zur Signalaufnahme wird ein 10 : 1 Oszilloskoptastkopf mit einem integrierten Wechselspannungsverstärker verbunden. Für den Tastkopf gilt Rv = 9 MΩ und Cv = 15 pF. Die Koaxialleitung zwischen Tastkopf und Verstärkereingang habe eine Länge l = 1,2 m und einen Kapazitätsbelag cK 0 von 50 pF/m. Abbildung .: Ersatzschaltbild der Eingangsbeschaltung (a) Zeichnen Sie das Ersatzschaltbild der Anordnung. (b) Berechnen Sie die inverse Übertragungsfunktion F −1 (jω ) = Ue (jω )/U a(jω ). (c) Der Verstärker hat die Eingangskapazität Ce = 68 pF. Dimensionieren Sie den Verstärker-innenwiderstand Re und die Trimmkapazität CT . F (jω ) soll in diesem Fall frequenzunabhängig sein. (d) Berechnen Sie für eine Frequenz von 10 MHz die Eingangsimpedanz ZEin des Tastkopfes, den eine Quelle am Eingang sieht. Vernachlässigen Sie dazu den ohmschen Anteil des Teilers. 1V fü r t ≥ 0 an den Tastkopf angelegt. Skizzieren Sie die 0V fü r t < 0 Spannung Ua (t) für drei die Fälle: CT zu groß, CT zu klein und CT bei Abgleich. (e) Es werde die Sprungfunktion ue (t) = (f ) Begründen Sie, warum eine Kabelverlängerung auf 1,5 m nicht mit CT zu kompensieren ist. Nennen Sie eine Möglichkeit, welcher Bauteilwert geändert werden muss, um den Abgleich bei dem verlängerten Kabel wieder zu erreichen. GEM Übung SS / Übung 12: Klausuraufgaben 12.1 Aufgabe 18 Aufgabe Operationsverstärker Als Eingangs-Bias-Strom wird bei Operationsverstärkern der Stromfluss in die Eingänge des OpAmps bezeichnet. Dieser wurde für einen neuen Operationsverstärker an vielen einzelnen Operationsverstärker-ICs gemessen. Der so charakterisierte Verstärkerchip soll nun in einer Messschaltung verwendet werden. Ig U1 If Rf VN Ia U2 Rg Ra VP Uout Id Rd Abbildung .: Operationsverstärker-Grundschaltung (a) Abbildung . zeigt eine Verstärkerschaltung mit einem zuvor charakterisierten Operationsverstärker. Benennen Sie diesen Schaltungstyp und berechnen Sie allgemein den Zusammenhang zwischen der Spannung Uout und den Spannungen U1 und U2 . Rg , Rf , Ra und Rd seien gegeben. Lösen Sie alle Doppelbrüche auf. (b) Geben Sie den Eingangswiderstand Rin1 der Schaltung aus Abbildung . von der Quelle U1 aus gesehen an, sowie den Eingangswiderstand Rin2 , den die Quelle U2 sieht. Lösen Sie alle Doppelbrüche auf. Hinweis: Beginnen Sie mit Rin2 . Nehmen Sie den OpAmp für diesen Aufgabenteil als ideal an. Gehen Sie davon aus, dass bei der Bestimmung von Rin1 die Spannung U2 beliebig, aber bekannt ist. Nehmen Sie an, dass die Schaltung stabil ist. Erneut seien alle Widerstandswerte gegeben. / GEM Übung SS Klausuraufgaben Ig U1 Rg VN Ib Ia U2 Rf If Ra I=0 I=0 Ib VP R i Uout Id Rd Abbildung .: Erweiterte Operationsverstärkerschaltung: Berücksichtigung des Bias-Stromes mit separaten Quellen und idealem OpAmp-Modell (c) Aufgrund der Eingangs-Bias-Ströme Ib ergibt sich bei Uout am Ausgang des Operationsverstärkers bei der Schaltung aus Abbildung . unter Umständen eine unerwünschte Offsetspannung. Berechnen Sie diese allgemein für den Fall U1 = U2 = 0. Ib , Rg , Rf , Ra und Rd seien gegeben. Gehen Sie dazu von dem Ersatzschaltbild aus Abbildung . aus, bei dem der Bias-Strom durch zusätzliche Quellen repräsentiert wird. Der Operationsverstärker in diesem Ersatzschaltbild sei als ideal angenommen (Ri = 0, I− = I+ = 0). Gehen Sie davon aus, dass die Schaltung stabil ist. Lösen Sie alle Doppelbrüche auf. Hinweis: Geben Sie zunächst eine Gleichung für den Ersatzwiderstand Rad der gemeinsamen Schaltung von Ra und Rd an und rechnen Sie mit diesem weiter. (d) Wie muss der Ersatzwiderstand Rad (und damit Ra und Rd ) in Abhängigkeit von den bekannten Größen gewählt werden, damit am Ausgang kein Offset auf Grund des Bias-Stromes Ib auftritt? Nutzen Sie das Ergebnis aus Punkt (c). (Rg +Rf )Rg Rf R R Falls Sie (c) nicht gelöst haben, rechnen Sie mit Uout = I − Rad Ib − fRgad Ib Rg (Rg +Rf ) b (e) Muss der Wert von Ra und Rd bei Einsatz eines Operationsverstärkers mit anderem Bias-Strom Ib angepasst werden? Begründen Sie Ihre Antwort kurz.