Zyklotron Theorie - Indico

PAUL SCHERRER INSTITUT
Zyklotron Theorie
• Zyklotron Schema
• Erste Zyklotron
• PSI Ringzyklotron
• Kraft auf Teilchen
• Kreisbahn im Zyklotron
• Homogenes Magnetfeld vom Zyklotron
• Klassisches Zyklotron
• Larmorfrequenz oder Umlauffrequenz
• Isochronzyklotron Parameter
• Kantenfokussierung vom Zyklotron
• Quadrupol wirkung
• Thomas-Zyklotron
• PSI Injektor 1 Zyklotron
• Instabiles 2-Sektor Zyklotron
• PSI Comet Zyklotron
• Schema Ringzyklotron
• Quadratzyklotron
• Prinzip Ringzyklotron
• Hochfrequenz Kavität
• Flattop Spannung
• Magnetfeld Ringzyklotron
• Hillfeld Ringzyklotron
• Feldprofil Ringzyklotron
• Numerische Bahnberechnungen
• Resonanzdiagramm
• Koppelresonanz
• Umläufe Ringzyklotron
• PSI Injektor 2 (72 MeV p)
• Vorbeschleuniger Injektor 2
• Injektor 2 Prinzip
• Letzte 5 Umläufe Injektor 2
• Extraktion aus Zyklotron
• Stromlimite Zyklotron PSI (über die Jahren)
• PSI Zyklotrons
• Comet Zyklotron (250 MeV p) Strahlentherapie
• Historisches Uebersicht Zyklotrons
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Zyklotron
Zyklotron Schema
Schema
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
1.
1. Zyklotron
Zyklotron 1931
1931
E.O.Lawrence, M.S.Livingston
Berkeley, Kalifornien
Durchmesser 4 inch
1 kV am Dee
80 keV Protonen
W.Joho Beschleuniger 2005
Ringzyklotron
Ringzyklotron590
590MeV
MeV
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Kraft auf Teilchen
Gesetz von Newton:
dp
dt
F,
p mJ v ( impuls)
Teilchen mit Ladung q im elektromagnetischen
Feld sieht Kraft F:
(1) Fel
qH
(2) Fm
q (v u B) ( Lorentzkraft durch Magnetfeld,
(elektrischesFeld ! Beschleunigung)
! Ablenkung)
Die magnetische Kraft ist immer senkrecht zu v und B
Ÿ es wird keine Arbeit geleistet !
Ÿ Geschwindigkeit v bleibt konstant
Vergleich:
Bei v = c:
E Ù vB
100 kV/cm Ù 0.033 T
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Kreisbahn
In homogenem Magnetfeld B läuft Teilchen auf
einer Kreisbahn mit Radius U
Balance zwischen Lorentzkraft FL und Zentrifugalkraft FZ:
FL
qvB ,
mit p
Fr
m v2
U
(nicht relativ.)
mv :
p=qBU
gilt auch relativistisch!
(BU = „magnetic rigidity“
Grundlage aller Kreisbeschleuniger (Zyklotron, Synchrotron,
Speicherring, Spektrometer etc. )
Für Elektronen mit E • 10 MeV: E[GeV] = pc= 0.3 BU[Tm]
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
homogenes
homogenes Magnetfeld
Magnetfeld
Teilchen mit Ladung q und Impuls p :
=> Kreisbahn mit Radius ȡ in homogenem Magnetfeld B
p=qBȡ
diese Kreisbahn kann überall platziert sein!
=> stabile horizontale Schwingung um Referenzbahn
mit Fokussierfrequenz Qr = 1
keine vertikale Stabilität (Qy = 0)
ȡ
·
Referenzbahn
Oszillation um
Referenzbahn
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Klassisches Zyklotron
In homogenem Magnetfeld sind die Kreisbahnen
vertikal instabil
Ÿ vertikale Stabilität durch radial abfallendes Feld B(r)
Definition eines Feldindexes n (dimensionslos)
durch „logarithmische Ableitung“
dB0
dr
(
) { n( )
B0
r
Fokussierfrequenzen : stabil für 0 n 1
Qr
1 n , Qy
n,
Qr2 Q y2
1
! schwache Fokussierung horizontal und vertikal
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Larmorfrequenz
Umlauffrequenz Z in homogenem Magnetfeld B:
(nicht relativ.) p = mv = q B R ,
q
B
m
Z0
v= R Z
( Larmorfrequenz )
Z ist unabhängig von radius R and Energie !
Ÿ Grundlage für klassisches Zyklotron (nicht relativistisch)
Allgemein gilt für alle Energien mit Etot = J mc2 und Z{SQ
Q0
(
q
)
B
2S m J
q
2S m
q
2S m
15 .25 MHz / T
für Protonen
28 GHz / T
für Elektronen
Beschleunigung mit Hochfrequenz auf harmonischer h:
QRF = h Q0
Ein isochrones Zyklotron hat Sektoren => B(r,-
B = B0(R) = Feld gemittelt über eine Umlaufbahn
=> B0(R) muss prop. zu J(R) anwachsen
[Alternative: Synchrozyklotron mit QRF(t) ]
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Parameter Isochronzyklotron
In isochronem Zyklotron:
R = v/Z0 ~ ȕ ,
Z0 = konstant
(ȕ = v/c)
absolute Radiuslimite für v=c: R’=c/Ȧ0
numerisch : Rf [m] h (
47.7 MHz )
R = ȕ R’
Für Protonen am PSI:
Q RF
)
Rmax = ȕmax R’
QRF = 50.7 MHz ,
R’ = h· 0.94m
E[MeV]
ȕmax
h
R’[m]
Rmax[m]
B0[T]
Injektor I
72
0.37
3
2.83
1.05
1.1
Injektor
II
Ring
72
0.37
10
9.40
3.5
0.33
590
0.79
6
5.65
4.5
0.55
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Kantenfokussierung
Kantenfokussierung
Sektormagnet mit
Kantenwinkel Ȍ
horizontal:
Teilchen mit paralleler Verschiebung x wird um
ds = x tan Ȍ später abgelenkt. => x‘ = ds/R
Die Wirkung ist wie ein defokussierender Quadrupol
der Stärke:
1/fx = -(1/R) tan Ȍ
vertikal:
fokussierend mit fy = - fx
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Quadrupol
aus Maxwell Gleichung
dBx
dy
dB y
dx
0:
rot B
G ( Gradient )
vertikal fokussierend :
Fy
q v Bx v G y
horizontal defokussierend :
Fx
q v By v G x
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Thomas-Zyklotron
Thomas-Zyklotron (1938)
(1938)
Sektoren auf Polplatte eines H-Magneten
=> vertikale Kantenfokussierung zwischen
Hill (H) und Valley (V)
Brennweite f y durch Kantenwinkel < :
1
fy
[ B ( H ) B (V )]
tan <
BU
( fx
fy)
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Injektor
Injektor II Zyklotron
Zyklotron
Philipps 1973
72 MeV Protonen
Ionen: Energie pro Nukleon
E/A=(Z/A)2 120 MeV
z.B. Deuteronen, Į : 30 MeV/Nukleon
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
instabiles
instabiles2-Sektor
2-SektorZyklotron
Zyklotron
instabile Bahn
Magnetsektor 1
geschlossene
Bahn
Magnetsektor 2
Resonanz der horiz. Fokussierfrequenz:
Qr = 2/2 (ʌ-mode stopband)
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Comet
Comet Zyklotron
Zyklotron
Magnetsektoren
Hochfrequenzsystem
8 x 80 kV
W.Joho Beschleuniger 2005
Ringzyklotron
Ringzyklotron
(Hans
(HansWillax
Willax1962)
1962)
Magnetfeld und HF-System entkoppelt
Kavitäten (auch Flattop)
mit hoher Spannung
starke vertikale Fokussierung
ökonomisch im Betrieb
erleichterte Konstruktion
der Injektion- und
Extraktions-elemente
Eisengewicht der Sektormagnete
vergleichbar mit Kompaktmagnet
viel Platz für Diagnostik
und Korrektur-elemente
kleiner Magnetspalt
gute Bahnseparierung,
kleine Extraktionsverluste
hohe Intensitäten
gerade Strecken
Nachteil:
Injektor notwendig !
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Quadratzyklotron
Quadratzyklotron
hypothetisch , da vertikal
überfokussierend !
Magnetsektor
HochfrequenzKavität
v1
R2
v2
Isochroniebedingung :
konstante Umlaufszeit für
alle Energien =>
v1/ v2 = R1/ R2
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Ringzyklotron
Ringzyklotron
Septum
Extraktion
Sektor
Magnet
HF-Kavität
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
HF-Kavität
HF-Kavität
Ringzyklotron 590 MeV , 50.7 MHz
Originalversion:
Aluminium , V=730 kV , 300 kW Verlustleistung
216 Umläufe
bei 2 mA: 300 kW Leistung/Kavität an Strahl
Azimuth
2.9 m
Radius
5.2 m
neue Kavität:
Kupfer , V = 1 MV , 500 kW Verlustleistung
160 Umläufe , Stromlimite > 3 mA ?
W.Joho Beschleuniger 2005
Flattop
Flattop Spannung
Spannung
W.Joho Beschleuniger 2005
y [mm]
2T
Ringzyklotron
Ringzyklotron
72
72--590
590MeV
MeVpp
Kontourlinien des
Magnetfeldes
mittleres Feld B0(R) ~ Ȗ
Zuwachs von 72-590 MeV :
55%
1.5 T
x [mm]
W.Joho Beschleuniger 2005
Hillfeld
HillfeldRingzyklotron
Ringzyklotron
20.9 kGauss
g = 50 mm
g = 80 mm
W.Joho Beschleuniger 2005
Ringzyklotron
Ringzyklotron
Feldprofil B(-)
r = 4m
r = 3m
r = 2m
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
nutzlos!
nutzlos!
Fokussierfrequenzen Qx und Qz im Isochron Zyklotron;
aus einem Bericht von Oak Ridge 1960
(so wollte man uns damals Angst machen!)
hier helfen nur numerische Bahnberechnungen.
Approximation:
Qz2 § -K + F (1+2 tan2į),
K=Feldindex, į=Spiralwinkel
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Resonanzdiagramm
Resonanzdiagramm
Ringzyklotron
Injektor I
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Koppelresonanz
Koppelresonanz
Ringzyklotron 590 MeV
Strahlverlust bei der Durchquerung der Koppelresonanz
bei 3 Energien: eine starke horizontale Schwingung wird
in eine vertikale Schwingung umgewandelt.
W.Joho Beschleuniger 2005
Ringzyklotron
Ringzyklotron(1980),
(1980),Umläufe
Umläufe26-315
26-315(100-590
(100-590MeV)
MeV)
W.Joho Beschleuniger 2005
Injektor
InjektorII
II (72
(72MeV
MeVp)
p)
W.Joho Beschleuniger 2005
Einschuss
Einschussin
inInjektor
InjektorII
II
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Injektor
Injektor IIII
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Letzte
Letzte 55 Umläufe
Umläufe im
im Injektor
Injektor IIII
Verbreiterung des Strahldurchmessers
durch longitudinale Raumladungskräfte
Extraktionsseptum
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Extraktion
Extraktion aus
aus Zyklotron
Zyklotron
Intensitätslimite eines Zyklotrons wird bestimmt durch die
Strahlverluste. Entscheidend ist der radiale Abstand dR/dn
der 2 letzten Bahnen vor der Extraktion
1
(1) E
m v2
2
1
m Z 2R2 ~ R2
(nichtrelativistisch)
2
(2) E | n q V
~ n (Umlaufszahl ) ,
HF Spannung pro Umlauf
V
dR
dn
! R ~ n,
dR
dn
J
J 1
R
R
2n
V
1
( E / e) Qr2
(exakte Formel)
grosse Bahnseparierung durch:
•
hohe HF-Spannung (Intensitätslimite ~ V3 !!)
•
grosser Maschinenradius !
=> keine hohen Intensitäten mit
kompaktem (supraleitendem) Zyklotron !!
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
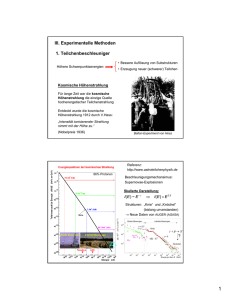
Stromlimite
Stromlimite in
in Zyklotron
Zyklotron
Stromlimite gegeben durch Extraktionsverluste (<0.4 µA)
Limite durch longitudinale Raumladung:
ILim ~ V3 ~ N-3
(W.Joho 1981)
V = Kavitätsspannung/Umlauf
N = Umlaufszahl
=> mit neuer Kavität : 730 kV => 1 MV (160 Umläufe!)
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
PSI Zyklotrons
INJEKTOR I
Leichte Ionen
E/A=(Z/A)2 K
K=120MeV
INJEKTOR II
Protonen 72MeV
200PA , 11PA polar.
Protonen 72MeV
2 mA (150kW)
COMET s.c.
Ringzyklotron
Protonen 250MeV
Strahlentherapie
Protonen 590MeV
2 mA (1.2 MW)
10PA polar.
• intensive Strahlen von Pionen und Müonen
• Spallations Neutronen Quelle (SINQ)
• Kernphysik
• Strahlentherapie mit Protonen
• Isotopen Produktion
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Comet-Zyklotron
Comet-Zyklotron (s.c.)
(s.c.)
250
250MeV
MeVProtonen
Protonen, ,Strahlentherapie
Strahlentherapie
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Zyklotron
Zyklotron historisch
historisch
W.Joho Beschleuniger 2005
PAUL SCHERRER INSTITUT
Vorträge Zyklotron
Vorträge von W.Joho
http://indico.psi.ch - Conferences Accelerator Talks
CERN Accelerator schools:
http:/cas.web.cern.ch/cas/
W. Joho: Modern Trends in Cyclotrons
CERN Accelerator School, Aarhus 1986
CERN 87-10
T. Stammbach:
CERN Accelerator School, LaHulpe 1994
CERN 96-02
International Cyclotron Conferences
(alle 3 Jahre)
Im Zyklotron Archiv
Allgemeine Vorlesung von Albin Wrulich über Beschleuniger
an der ETH Lausanne:
http://people.web.psi.ch/wrulich
W.Joho Beschleuniger 2005