Kapitel 3: Berechnungstheorie Algorithmisch unlösbare Probleme

Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Einordnung
•
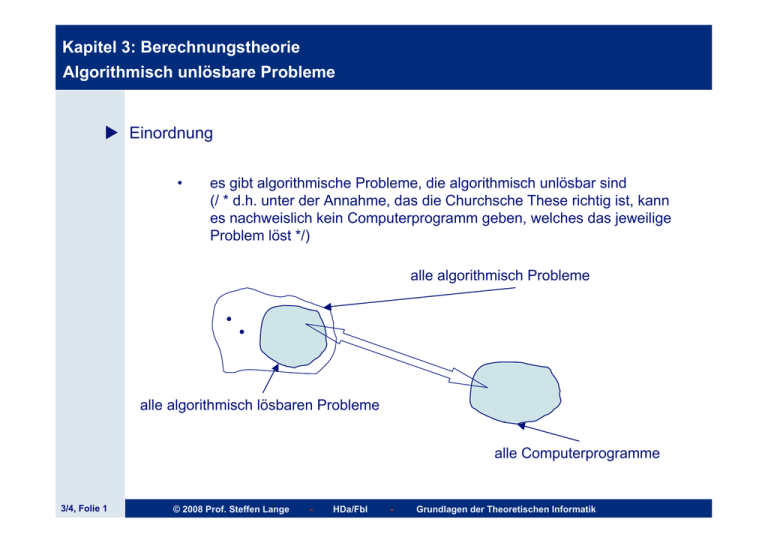
es gibt algorithmische Probleme, die algorithmisch unlösbar sind
(/ * d.h. unter der Annahme, das die Churchsche These richtig ist, kann
es nachweislich kein Computerprogramm geben, welches das jeweilige
Problem löst */)
alle algorithmisch Probleme
alle algorithmisch lösbaren Probleme
alle Computerprogramme
3/4, Folie 1
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Fahrplan
•
zwei algorithmische Probleme kennen lernen und den Nachweis ihrer
algorithmischen Unlösbarkeit führen
... Verständnis für die Grenzen von Computerprogrammen entwickeln
... zentrale Beweisideen kennen lernen
Geben Sie einem Computer die richtige Software und er wird tun,
was immer Sie wünschen. Die Maschine selbst mag ihre Grenzen
haben, doch für die Möglichkeiten von Software gibt es keine
Grenzen.
Time-Magazine, 1984
3/4, Folie 2
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Problem 1: Halteproblem für TM-Programme
zulässige Eingaben:
•
•
TM-Programm T
eine Zahl x ∈ N
zulässige Ausgaben:
•
•
die Zahlen 0 oder 1
eine 1 soll ausgegeben werden, wenn das
TM-Programm T bei Eingabe von bin(x)
den Endzustand erreicht
eine 0 soll ausgegeben werden, wenn das
TM-Programm T bei Eingabe von bin(x)
nicht den Endzustand erreicht
•
3/4, Folie 3
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Problem 2: Äquivalenzproblem für TM-Programme
zulässige Eingaben:
•
•
TM-Programm T1
TM-Programm T2
zulässige Ausgaben:
•
•
die Zahlen 0 oder 1
eine 1 soll ausgegeben werden, wenn das
TM-Programm T1 und das TM-Programm T2
dieselbe Funktion über den natürlichen
Zahlen berechnen
eine 0 soll ausgegeben werden, wenn das
TM-Programm T1 und das TM-Programm T2
nicht dieselbe Funktion über den natürlichen
Zahlen berechnen
•
... T1 und T2 berechnen dieselbe Funktion fT1 bzw. fT2, falls für alle x ∈ N gilt:
•
wenn fT1(x) definiert ist, so ist fT1(x) = fT2(x)
•
wenn fT1(x) undefiniert ist, so ist auch fT2(x) undefiniert
3/4, Folie 4
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Anmerkungen
•
Relevanz der Probleme (/* analog kann man über das Halteproblem
bzw. das Äquivalenzproblem für C++-Funktionen reden ... */)
Einordnung in unsere begriffliche Welt (/* jedem diese Probleme eine
Funktion über den natürlichen Zahle zuordnen und nachweisen, daß
diese Funktion nicht TM-berechenbar ist */)
•
 Schwierigkeiten
1.
2.
3/4, Folie 5
Zusammenhang zwischen TM-Programmen und Zahlen ...
zulässige Eingaben sind eigentlich Paare von Zahlen (/* falls obiges
geklärt ist */)
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 1. Schwierigkeit
•
übliche Idee in Programmiersprachen – Verwendung von Namen für
Funktionen (/* Zahlen können dieselbe Rolle wie Namen spielen */)
... es gibt nur abzählbar viele Namen
... es gibt nur abzählbar viele TM-Programme
•
•
3/4, Folie 6
es sei T0,T1,T2, ... eine effektive Aufzählung aller TM-Programme;
insbesondere gilt für alle a, b ∈ N und alle TM-Programm T:
•
wenn a ≠ b, so sind Ta und Tb (syntaktisch) verschieden
•
man kann effektiv ein a ∈ N mit Ta = T finden
jedes a ∈ N spielt die Rolle des eindeutigen Namens für das TMProgramm Ta
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 2. Schwierigkeit
•
3/4, Folie 7
es gibt eine berechenbare Funktion cod(.,.), um Paare natürlicher
Zahlen eineindeutig als natürliche Zahl zu kodieren sowie passende
berechenbare Funktion d1(.) und d2(.) zum decodieren
x
y
cod(x,y)
0
0
0
0
1
1
1
0
2
0
2
3
1
1
4
2
0
5
0
3
6
1
2
7
2
1
8
...
...
...
© 2008 Prof. Steffen Lange
Codierung:
cod(x,y) = x + (x+y)*(x+y+1)/2
Decodierung (/* es sei z = cod(x,y) */):
d1(z) = z - u(z)*u(z+1)/2
d2(z) = u(z) - d1(z)
u(z) = max { k | k*(k+1)/2 ≤ z }
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Problem 1: Halteproblem für TM-Programme (/* angepaßt */)
zulässige Eingaben:
•
Zahl z ∈ N mit z = cod(k,x)
zulässige Ausgaben:
•
•
die Zahlen 0 oder 1
eine 1 soll ausgegeben werden, wenn das
TM-Programm Tk bei Eingabe von bin(x)
den Endzustand erreicht
eine 0 soll ausgegeben werden, wenn das
TM-Programm Tk bei Eingabe von bin(x)
nicht den Endzustand erreicht
•
3/4, Folie 8
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Problem 2: Äquivalenzproblem für TM-Programme (/* angepaßt */)
zulässige Eingaben:
•
Zahl z ∈ N mit z = cod(a,b)
zulässige Ausgaben:
•
•
die Zahlen 0 oder 1
eine 1 soll ausgegeben werden, wenn
das TM-Programm Ta und das TMProgramm TM Tb dieselbe Funktion über
den natürlichen Zahlen berechnen
eine 0 soll ausgegeben werden, wenn das
TM-Programm TM Ta und das TMProgramm TM Tb nicht dieselbe Funktion
über den natürlichen Zahlen berechnen
•
3/4, Folie 9
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 ... um uns das Leben einfacher zu machen (/* Teil 1 */)
•
•
es sei f(.) eine Funktion von N nach N
es sei T ein TM-Programm, das f(.) berechnet
•
dann gibt es wegen der Churchschen These auch eine C++Funktion func(nat), so daß für alle x ∈ N gilt:
•
•
3/4, Folie 10
wenn fT(x) definiert ist (/* d.h. T erreicht bei Eingabe von bin(x)
den Endzustand */), so gibt func(nat) bei Eingabe von x den
Wert y = fT(x) zurück
wenn fT(x) undefiniert ist (/* d.h. T erreicht bei Eingabe von
bin(x) den Endzustand nicht */), so gibt func(nat) bei Eingabe
von x keinen Wert zurück
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 ... um uns das Leben einfacher zu machen (/* Teil 2 */)
•
•
es sei f(.) eine Funktion von N nach N
es sei func(nat) eine C++ Funktion, die f(.) berechnet
•
dann gibt es wegen der Churchschen These auch ein TMProgramm T, so daß für alle x ∈ N gilt:
•
•
3/4, Folie 11
wenn func(nat) bei Eingabe von x den Wert y zurück gibt, so
gilt fT(x) = y
wenn func(nat) bei Eingabe von x keinen Wert zurück gibt, so
erreicht T bei Eingabe von bin(x) nicht den Endzustand
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 ... was bringt das für Vorteile
... Unterprogrammaufrufe können in der C++-Welt leichter nachvollziehbar
beschrieben werden
•
•
•
es sei func_1(nat) eine C++-Funktionen
es sei func(nat) die folgende C++-Funktion
es x ∈ N
•
nat func ( nat x ) {
nat a;
a = func_1(x);
return(a+1);
}
3/4, Folie 12
© 2008 Prof. Steffen Lange
-
falls func_1(nat) bei Eingabe von x einen Wert y1
zurück gibt, so gibt func(nat) den Wert y1+1
zurück
falls func_1(nat) bei Eingabe von x keinen Wert
zurück gibt, so gibt func(nat) keinen Wert zurück
•
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 ... was bringt das Vorteile
... die Nacheinanderausführung von Programmen kann in der C++-Welt
leichter nachvollziehbar beschrieben werden
•
•
•
es seien func_1(nat) und func_2(nat) C++-Funktionen
es sei func(nat) die folgende C++-Funktion
es x ∈ N
nat func ( nat x ) {
nat a,b;
a = func_1(x);
b = func_2(a);
return(b);
}
•
•
•
3/4, Folie 13
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
falls func_1(nat) bei Eingabe von x einen Wert
y1 und func_2(nat) bei Eingabe von y1 einen
Wert y2 zurück gibt, so gibt func(nat) den Wert
y2 zurück
falls func_1(nat) bei Eingabe von x einen Wert
y1 und func_2(nat) bei Eingabe von y1 keinen
Wert zurück gibt, so gibt func(nat) keinen Wert
zurück
falls func_1(nat) bei Eingabe von x keinen
Wert zurück gibt, so gibt func(nat) keinen Wert
zurück
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Das Halteproblem ist algorithmisch unlösbar
Es gibt kein TM-Programm T, das das Halteproblem für TM-Programme
löst, d.h. die unten definierte Funktion f(.) über den natürlichen Zahlen
berechnet.
Für alle k,x ∈ N gilt:
1,
falls das TM-Programm Tk bei Eingabe von
bin(x) den Endzustand erreicht
0,
falls das TM-Programm Tk bei Eingabe von
bin(x) nicht den Endzustand erreicht
f(cod(k,x)) =
•
•
3/4, Folie 14
es sei T0,T1,T2, ... eine effektive Aufzählung aller TM-Programme
es sei func_0(nat),func_1(nat),func_2(nat),... die zugehörige
Aufzählung von C++-Funktionen
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* indirekt mittels Diagonalisierung */)
•
•
Annahme: es seien T ein TM-Programm, das die Funktion f(.) berechnet ,
und func(nat) die zugehörige C++-Funktion
es sei func*(nat) die wie folgt beschriebene C++-Funktion
nat func* ( nat x ) {
nat z,a,y;
z = cod(x,x);
a = func(z);
if ( a = 0 )
{ return(0); }
else
{ y = func_x(x); return(y+1); }
}
3/4, Folie 15
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Aufruf von func(nat); gibt bei
Eingabe von z = cod(x,x) eine 1
zurück, falls die C++-Funktion
func_x(nat) bei Eingabe von x
einen Wert zurück gibt; sonst
wird eine 0 zurück gegeben
Aufruf von func_x(nat); wird nur
aufgerufen, falls die C++-Funktion
func_x(nat) bei Eingabe von x
einen Wert zurück gibt
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* cont. */)
•
offenbar gilt für alle x ∈ N, daß sich die C++-Funktionen func*(nat) und
func_x(nat) unterschiedlich verhalten
 bei Eingabe von x ∈ N gilt:
•
•
•
•
•
•
falls func_x(nat) den Wert y zurück gibt, so gibt func*(nat)
den Wert y+1 zurück
falls func_x(nat) keinen Wert zurück gibt, so gibt func*(nat)
den Wert 0 zurück
es sei T* das zur C++-Funktionen func*(nat) gehörende TM-Programm
da T0,T1,T2, ... eine effektive Aufzählung aller TM-Programme ist, muß es
ein z ∈ N mit Tz = T* geben
also berechnen die TM-Programme T* und Tz dieselbe Funktion f*(.)
also verhalten sich die C++-Funktionen func*(nat) und func_z(nat) gleich
zu oben
3/4, Folie 16
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Das Äquivalenzproblem ist algorithmisch unlösbar
Es gibt kein TM-Programm T, das das Äquivalenzproblem für TMProgramme löst, d.h. die unten definierte Funktion f(.) über den
natürlichen Zahlen berechnet.
Für alle a,b ∈ N gilt:
1,
falls das TM-Programm Ta und das TMProgramm Tb dieselbe Funktion berechnen
0,
falls das TM-Programm Ta und das TMProgramm Tb nicht dieselbe Funktion
berechnen
f(cod(a,b)) =
•
•
3/4, Folie 17
es sei T0,T1,T2, ... eine effektive Aufzählung aller TM-Programme
es sei func_0(nat),func_1(nat),func_2(nat),... die zugehörige
Aufzählung von C++-Funktionen
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* direkt mittels Reduktion */)
•
wir werden folgenden Zusammenhang beweisen
Jedes TM-Programm, das das Äquivalenzproblem für TM-Programme löst,
kann verwendet werden, um das Halteproblem für TM-Programme zu lösen.
... da es kein TM-Programm gibt, das das Halteproblem für TuringMaschinen löst, kann es auch kein TM-Programm geben, das das
Äquivalenzproblem für Turing-Maschinen löst
3/4, Folie 18
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* cont. */)
3/4, Folie 19
•
es seien k,x ∈ N, d.h. es interessiert uns, ob das TM-Programm Tk bei
Eingabe von bin(x) den Endzustand erreicht
•
•
es sei func_k(nat) die zum TM-Programm Tk gehörige C++-Funktion
wir definieren die folgenden zwei C++-Funktionen func_kx1(nat) und
func_kx2(nat)
nat func_kx1 ( nat z ) {
return(0) }
}
die C++-Funktion func_kx1(nat) gibt
bei Eingabe jedes z ∈ N den Wert 0
zurück
nat func_kx2 ( nat z ) {
nat y;
y = func_k(x);
return(0);
}
Aufruf von func_k(nat); falls die C++Funktion func_k(nat) bei Eingabe von x
einen Wert zurück gibt, so gibt die C++Funktion func_kx2(nat) bei Eingabe
jedes z ∈ N den Wert 0 zurück; sonst
gibt func_kx2(nat) bei Eingabe keines
z ∈ N einen Wert zurück
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* cont. */)
•
es seien k,x ∈ N, d.h. es interessiert uns, ob das TM-Programm Tk bei
Eingabe von bin(x) den Endzustand erreicht
•
es seien Tkx1 die zu func_xk1(nat) und Tkx2 die zu func_xk2(nat)
gehörenden TM-Programme
offenbar berechnen das TM-Programm Tkx1 und das TM-Programm
Tkx2 genau dann dieselbe Funktion, wenn Tk bei Eingabe von bin(x)
den Endzustand erreicht
•
3/4, Folie 20
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 3: Berechnungstheorie
Algorithmisch unlösbare Probleme
 Beweis (/* cont. */)
•
•
•
da T0,T1,T2, ... eine effektive Aufzählung aller TM-Programme ist, muß es
a,b ∈ N mit Ta = Tkx1 und Tb = Tkx2 geben
es sei T ein TM-Programm, das das Äquivalenzproblem für TuringMaschinen löst
offenbar gilt:
•
•
T berechnet bei Eingabe von bin(cod(a,b)) eine 1, falls das TMProgramm Ta und das TM-Programm Tb dieselbe Funktion
berechnen, d.h. falls Tk bei Eingabe von bin(x) den Endzustand
erreicht
T berechnet bei Eingabe von bin(cod(a,b)) eine 0, falls das TMProgramm Ta und das TM-Programm Tb nicht dieselbe Funktion
berechnen, d.h. falls Tk bei Eingabe von bin(x) nicht den
Endzustand erreicht
... also löst das TM-Pogramm T „nebenbei“ das Halte-Problem für
Turing-Maschinen
3/4, Folie 21
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik