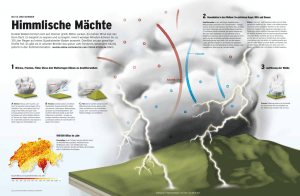
Abschätzung des Einflusses von Aerosolen oberhalb

Abschätzung des Einflusses von Aerosolen
oberhalb maritimem Sc auf die
Strahlungsbilanz im solaren Spektralbereich
Diplomarbeit
von Antonia Haser
eingereicht am Fachbereich Geowissenschaften
der Freien Universität Berlin
Januar 2009
2
3
für Frederik H.
4
Inhaltsverzeichnis
1 Einleitung
7
1.1
Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
1.2
Ziel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2 Grundlagen
13
2.1
Strahlungshaushalt . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
2.2
Strahlung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.3
Strahlungstransportgleichung . . . . . . . . . . . . . . . . . . . . . . .
16
3 Satelliten- und Modelldaten
19
3.1
Meteosat Second Generation . . . . . . . . . . . . . . . . . . . . . . . .
19
3.2
A-Train . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3.2.1
CloudSat
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3.2.2
CALIPSO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
3.2.3
MODIS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
3.3
OPAC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
3.4
GFS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
3.5
Strahlungstransportmodell MOMO . . . . . . . . . . . . . . . . . . . .
24
3.6
Wolken . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
4 Simulationen
29
5 Ergebnisse
35
5.1
Messdaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
5.2
Ursprung der Aerosole . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
5.3
Wolkenoptische Dicke . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
5.4
Simulationsergebnisse und Auswertung . . . . . . . . . . . . . . . . . .
40
6 Zusammenfassung
49
5
6
INHALTSVERZEICHNIS
7 Anhang
51
7.1
Normierter Strahlungsfluss
. . . . . . . . . . . . . . . . . . . . . . . .
52
7.2
Tagesgang des Strahlungsflusses in W/m² . . . . . . . . . . . . . . . .
54
7.3
Heizraten pro Tag . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
8 Danksagung
59
9 Abkürzungen und Quellen der Abbildungen
61
9.1
Abkürzungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
61
9.2
Quellen der Abbildungen . . . . . . . . . . . . . . . . . . . . . . . . . .
62
10 Literaturverzeichnis
63
Kapitel 1
Einleitung
Die Entwicklung des Klimas und der anthropogen verursachte Anteil daran werden in den letzten Jahren immer stärker diskutiert. Es gibt Berechnungen über einen
weiteren Anstieg der globalen Durchschnittstemperatur um 4 bis 6°K und ein damit
verbundenes Aussterben von bis zu 30% der Pflanzen- und Tierarten. Bei Modellrechnungen für die Klimaentwicklung und den damit verbundenen Meeresspiegelanstieg für
die kommenden Jahrzehnte ergeben sich regelrechte Horrorszenarien. Fest steht, dass
die globalen Temperaturen seit vorindustrieller Zeit bereits um 2-3°K angestiegen sind.
Die antropogene Treibhausgasemission ist um 70%, der Ausstoß von CO2 sogar um
80% im Zeitraum von 1970 bis 2004 angestiegen. Dies ist nicht zu widerlegen. Laut
IPCC 2007 wäre bei einem Temperaturanstieg um weitere 2-3°C mit einer Häufung
von Extremwettererscheinungen zu rechnen.
Um dieser Entwicklung entgegen zu wirken, hat die europäische Kommission auf
der Weltklimakonferenz in Bali 2007 das Ziel einer Reduktion des Ausstoßes der Treibhausgase um 50% bis zum Jahr 2050 festgelegt. Nicht alle Länder sehen eine Notwendigkeit dieser Maßnahme gegeben. Das Geoengineering rückt somit immer häufiger in
den Mittelpunkt von Klimadiskussionen. Schwefelwolken in der Stratosphäre, Weiße
Wolken durch in die Luft geschossene Wassertröpfchen oder ein Sonnensegel im All
sollen die solare Einstrahlung verringern und somit eine weitere Erwärmung der Erdtemperatur dämpfen oder gar ganz stoppen. Auch wird die Bindung des CO2 aus der
Luft im Ozean oder unterirdischen Reservoirs diskutiert. Hier zeigt sich für manch einen
Politiker eine einfache Lösung für ein doch sonst so unangenehmes Thema auf. Viele
Wissenschaftler sehen aber große Risiken in diesen Eingriffen in unsere Erdatmosphäre. Simone Tilmes, vom National Center for Atmospheric Research (NCAR) warnt,
dass das Einbringen von Schwefel in die Stratosphare die Ozonschicht negativ beein7
8
KAPITEL 1. EINLEITUNG
flussen könnte (Tilmes, 2008). Salzwassertröpfchen, die in die Atmosphäre geschossen
werden, erhöhen zwar die Anzahl der Teilchen, was die Albedo der Wolken vergrößern
soll, aber verändern auch das Niederschlagsverhalten und damit die Lebensdauer der
Wolken. Bei der Erforschung möglicher Auswirkungen des Geoengineering steht man
noch am Anfang. Wichtig ist es die bereits vorhandenen Prozesse des Erdsystems zu
verstehen. Aerosole können zum Beispiel die Albedo der Wolke verändern, indem die
als zusätzliche Kondensationskerne in der Wolke dienen. Dies ist der erste indirekte
Aerosoleffekt.
Abb. 1.1 Amerikanische Wissenschaftler haben alle Brände des Zeitraumes vom 09.08.2006 bis
18.08.2006 aufgezeichnet und in einer Weltkarte katalogisiert. Jeder rote Punkt steht für mindestens
einen detektierten Brand, in den gelben Gebieten ist die Zahl der detektierten Brände hoch, was
man zum Beispiel im südl. Afrika sieht.
Der Eingriff des Menschen in die Natur ist aber auch in anderen Gebieten deutlich
zu erkennen. Allerdings hat nicht jeder dieser Eingriffe eine für das Klima positive Intention wie das Geoengineering. Laut WWF werden heutzutage 95% aller Wald- und
Buschfeuer vom Menschen verursacht. Zu diesen Feuern zählen neben den kontrollierten Feuern, wie das Abbrennen von Feldern oder Rodungsfeuer auch die Großfeuer
der US-amerikanischen Westküste, die Feuer des Mittelmeerraums und die saisonalen
Buschbrände in Afrika (siehe Abb. 1.1). Allein im Mittelmeerraum brennen jährlich
ca. 800.000 Hektar Wald, was einer Fläche der Größe Kretas entspricht. Die Folgen
von Waldbränden können sehr unterschiedlich sein. Im kleinen Ausmaß bei natürlichen
Bränden stellen sie einen wichtigen Beitrag zur Regeneration des Waldes dar. In besiedelten und bewirtschafteten Gebieten bedrohen die Feuer immer wieder den Wohnraum
und die Einkommensquellen von Menschen. Der Einfluss des Feuers erstreckt sich bis
weit in die Atmosphäre. Dort werden die durch das Feuer entstandenen rußhaltigen Aerosole durch die Winde oft über weite Strecken transportiert. Die Rauchfahnen fächern
sich auf und die von den Aerosolen bedeckte Fläche vergrößert sich. Jedoch verringert
9
sich durch das Auffächern die optische Dicke der Aerosolschicht. Klar ist, dass die Aerosole einen Einfluss auf die Strahlungsbilanz der Erde haben. Ob dieser durch das
Auffächern verstärkt wird, muss noch untersucht werden.
Abb. 1.2 Die Abb. zeigt eine Aufnahme des NASA Satelliten Aqua VIS vom 26.08.2007. Zu
erkennen sind das griechische Festland und einige Inselgruppen. Die roten Linien markieren die
Brandherde. Auch sichtbar sind die weißlichen Rauchfahnen. Statt einem sehr dunklen Untergrund
(Wasser) sind helle Aerosolschichten aus Rußpartikeln zu sehen. Hier zeigt sich schon bei einer
einfachen Aufnahme in Fotoqualität eine starke Veränderung der Albedo.
Aerosole haben zwar einen kleineren Einfluss auf die Strahlungsbilanz als Wolken,
der Effekt der entsteht, wenn sich eine dunkle Aerosolschicht über eine helle Wolkenschicht schiebt, ist aber nicht zu vernachlässigen. Sie können in Abhängigkeit ihrer
optischen Eigenschaften die Strahlung reflektieren und/oder absorbieren, was sich je
nach Helligkeit des Untergrunds unterschiedlich bemerkbar macht (siehe Abbn. 1.2,
1.3). Die Unterschiedlichkeiten der Aerosole finden ihren Ursprung in ihrer chemischen
Zusammensetzung, Form und Größe. Auch die Entstehungsprozesse der Aerosole sind
verschieden. Sie gelangen durch Winde in die Atmosphäre und beeinflussen den Strahlungshaushalt. Das in dieser Arbeit betrachtete Aerosol ist organischen Ursprungs. Es
entsteht bei der Verbrennung von Biomasse und wird daher als biomass burning aerosol
bezeichnet. Es ist stark absorbierend. Je nach Zusammensetzung des Brennmaterials
und Art des Brennvorgangs weisen auch diese Aerosole Unterschiede auf. Erhalten
bleibt die Hauptkomponente Ruß. So wurden bei einer Messkampagne im Jahr 2000
(SAFARI) optische Dicken für biomass burning aerosols gemessen, die zwischen 0.4
und 2.5 variierten (Eck et al., 2003).
10
KAPITEL 1. EINLEITUNG
Abb. 1.3 Gerade rußhaltige Aerosole kommen mit ihrer absorbierenden Wirkung vor allem über
sehr hellen Untergründen zum Tragen. Schaut man sich die Aerosole in Vergleich mit einer Wolke
an, so ist das absorbierende Verhalten der Aerosole durch ihre dunklere Färbung zu erkennen. Die
Abbildung zeigt die Rauchfahnen vom 27.08.2007. Die weißgrauen Rauchfahnen des Vortages sind
durch die Winde auf größere Fläche verteilt und zeigen ihre dunklere Färbung gegenüber den weißen
Wolken.
1.1
Motivation
Feuer und damit auch rußhaltige Aerosole entstehen in Afrika aus vielen Gründen.
Zum Einen werden Feuer für die jährliche Wiederherstellung vorhandener Ackerflächen genutz, zum Anderen werden durch Brandrodung neue Weide- und Ackerflächen
geschaffen. Ein weiterer Punkt ist, dass in Afrika Holz immer noch die wichtigste Energiequelle ist. Die Verbrennung von Biomasse ist global gesehen die größte Kohlenstoffemissionsquelle.Aber auch die natürlichen Wald- und Steppenfeuer in Afrika sind
für die Aerosolbildung und deren Auswirkungen nicht zu vernachlässigen, müssen also
auch betrachtet werden. Während der SAFARI 2000 Kampagne verbrannten in 31.000
Großfeuern rund 256.000 km2 in den Monaten August und September. Der saisonale
Höhepunkt für Großbrände in Afrika lag allerdings schon in den Monaten Juni und Juli. Der Einfluss der hier entstandenen Aerosole ist in verschiedenen Bereichen wichtig.
Über Meeresgebieten werden die Wechselwirkungen zwischen Wolken und Aerosolen
verändert und der Strahlungshaushalt beeinflusst. Die Niederschlagswahrscheinlichkeit
über Land wird ebenfalls verändert. Die Aerosole verändern die Teilchenkonzentration
und den effektiven Partikelradius der Wolken, was sich wiederum auf die Lebensdauer
und Regenwahrscheinlichkeit der Wolken auswirkt. Zu Beginn dieser Arbeit war es das
Ziel, diese mikrophysikalischen Eigenschaften von Stratokumuluswolken genauer zu untersuchen. Diese Aufgabe konnte aber wegen technischer Probleme und nicht genügend
ausgereiften Datenprodukten des Satelliten CloudSat im Rahmen einer Diplomarbeit
nicht bearbeitet werden. Aus zeitlichen Gründen wurde das Thema daher so umstruk-
1.2. ZIEL
11
turiert, dass die Arbeit unabhängig von externen Datenprodukten angefertigt werden
konnte. Die verwendeten Daten sind als Zusatzinformationen zu der durchgeführten
Sensitivitätsstudie zu betrachten. Sie sollen ihr einen realen Rahmen geben.
1.2
Ziel
Von den Stratokumuluswolken ist bekannt, dass sie ca. 30% der solaren Strahlung
reflektieren. Dies führt vor allem über dunklen Flächen wie dem Ozean zu einer geringeren Energieaufnahme in den Schichten unterhalb so einer Wolke. Der Einfluss der
Aerosole auf den solaren Strahlungshaushalt ist hingegen noch nicht genau bekannt.
In dieser Arbeit soll nun analysiert werden, welchen Einfluss das biomass burning aerosol auf den Strahlungshaushalt hat. Eine Auswertung der ersten zweieinhalb Jahre
MODIS Messungen(Juli 2002 bis Dezember 2004) hat gezeigt, dass die mikrophysikalischen Eigenschaften der Wolken über dem südöstlichen Atlantik stark durch die
afrikanische Waldbrandsaison beeinflusst werden (Bennartz, 2007). Die durchgeführten Simulationen mit dem Strahlungstransportmodell MOMO werden anhand einer
Fallstudie aufgebaut. Das Gebiet der Fallstudie ist der Golf von Guinea. Dieser befindet sich am nördlichen Ausläufer des Benguelastroms. Die kalten Meeresströmungen
die entlang der afrikanischen Westküste an die Oberfläche treten, begünstigen die Entstehung von langlebigen Stratokumulusfeldern. Ähnlich wie an der südamerikanischen
Westküste entlang der Atacamawüste, gibt es auch hier aufsteigendes, kühles Tiefenwasser und absinkende Luftmassen, die eine stärkere vertikale Ausbreitung der Wolken
verhindern. Somit entstehen die breiten Stratokumulusfelder. Das in der Arbeit betrachtete Gebiet ist, dank der fast täglich vorhandenen Stratokumuluswolken und der
während der Waldbrandsaison sehr häufig vorhandenen Aerosole, ideal für meine Arbeit geeignet. Diese Arbeit soll einen Beitrag zum besseren Verständnis des direkten
Aerosoleffektes über Wolken leisten.
12
KAPITEL 1. EINLEITUNG
Kapitel 2
Grundlagen
In diesem Kapitel sollen die für diese Arbeit wesentlichen theoretischen Grundlagen vorgestellt werden. Dazu gehören der Strahlungshaushalt, das solare Spektrum, in
dessen spektralem Bereich meine Berechnungen stattfanden, eine Beschreibungen von
Absorption, Emission und eine ausführliche Darstellung der Strahlungstransportgleichung.
2.1
Strahlungshaushalt
Befindet sich die Erde im Strahlungsgleichgewicht, so heben sich die solare Einstrahlung und die Ausstrahlung bestehend aus thermaler Abstrahlung und reflektierter solarer Strahlung, auf. Dies gilt nur global gesehen, da sich die Netto-Einstrahlung
bzw. Ausstrahlung am Äquator und an den Polen stark voneinander unterscheiden.
Die Strahlungsbilanz entlang eines Breitengrades ist nicht ausgeglichen. Niedrige Breiten erhalten mehr solare Einstrahlung als die Polregionen. Zusätzlich reflektieren eisund schneebedeckte Flächen in den hohen Breiten mehr Sonnenlicht als dunkles Land
oder fast schwarzes Wasser. Durch diese Unterschiede entsteht ein ausgeprägter Temperaturgradient zwischen Pol und Äquator. Die thermale Abstrahlung der Erde wirkt
diesem Trend zwar entgegen, kann ihn aber wegen seiner Stärke nicht kompensieren.
Das hieraus entstehende Ungleichgewicht ist die Grundlage für die großen Zirkulationsräder (Hadley - Zelle, Ferrel - Zelle und Polarzelle).
Wolken haben ebenfalls einen großen Einfluss auf den Strahlungshaushalt der Erde.
Hohe Wolken, wie der Zirrus, sind im solaren Spektralbereich als dünn anzusehen. Sie
lassen fast die gesamte einfallende Strahlung passieren. Im terrestrischen Spektralbereich dagegen sind diese Wolken optisch dick (fast schwarz). Sie absorbieren die aufwärts
13
14
KAPITEL 2. GRUNDLAGEN
Abb. 2.1 Strahlungshaushalt der Erde (entnommen aus dem IPCC-Report 2001). Dargestellt ist
die solare Einstrahlung in gelb und die langwellige thermale Ausstrahlung in rot. Die Werte sind in
W/m² angegeben. Die Pfeile geben die Strahlungsrichtung an.
gerichtete Ausstrahlung der Erde. Zirruswolken haben somit eine wärmende Wirkung
auf das Erdsystem. Den Gegensatz dazu bilden die tiefen Wolken wie der Stratokumulus. Auch diese Wolkenart ist im terrestrischen Sprektralbereich absorbierend, hat aber
in solaren Spektralbereich eine reflektierende Wirkung. Diese reflektierende Wirkung
der tiefen Wolken ist so stark ausgeprägt, dass tiefe Wolken einen kühlenden Einfluss
auf die Erde haben. Der Nettoeinfluss der Flüssigwasserwolken auf den Strahlungsfluss
wird mit -0.7 W/m² angegeben (Forster et al., 2007). Das bedeutet, das ohne diese
stark reflektierenden Wolken, die globale Temperatur auf der Erde signifikant höher
wäre.
2.2
Strahlung
Im allgemeinen wird Strahlung als die Ausbreitung von elektromagnetischen Wellen
oder im Teilchenmodell durch Photonen beschrieben. Diese Wellen/Photonen werden
beim Auftreffen auf ein Hindernis gestreut oder absorbiert.
Wenn Strahlung auf Materie (Moleküle oder Festkörper wie Aerosole und Boden)
trifft, finden verschiedene Arten von Wechselwirkung statt. Die Energie des Photons
wird an das Hindernis übertragen. Das getroffene Molekül geht in einen höheren Energiezustand (zum Beispiel höherer Rotations- oder Schwingungszustand) über. Die Abgabe dieser Energie und der damit zusammenhängende Übergang in den Ausgangszustand findet auf unterschiedliche Arten statt. Bei einer spontanen Energieabgabe
sendet das Molekül ein Photon aus, das sich nur in der Richtung seiner Bewegung von
2.2. STRAHLUNG
15
Abb. 2.2 Das solare Spektrum ist stark wellenlängenabhängig. Die graue Kurve beschreibt das
Strahlungsverhalten eines Schwarzkörpers mit einer Temperatur von 5250°C. Dies ist eine gute
Approximation der solaren Strahlung am Oberrand der Atmosphäre, die durch die gelbe Fläche
dargestellt ist. Die rote Fläche beschreibt die Strahlung auf Meeresniveau nach Durchgang durch die
absorbierende Atmosphäre (siehe violette Beschriftung). Die solare Strahlung hat ihr Maximum im
sichtbaren Bereich. Im ultra-violetten Spektralbereich absorbiert Ozon (O3 ) die solare Strahlung, im
infraroten Bereich findet man starke Absorptionsbanden des Wasserdampfes.
dem ursprünglichen Photon unterscheidet. Dieser Vorgang wird Streuung genannt.
Findet Streuung am Boden oder an Wolkenteilchen (in den rückwärtigen Raum) statt,
spricht man von Reflexion. Wird die Energie nicht spontan, sondern verzögert abgegeben, heißt der Effekt Fluoreszenz und Phosphoreszenz. Wenn ein Photon seine Energie
an die Maretie abgibt, wird dies als Absorption bezeichnet. Dies führt zur Erwärmung
des Gases/Festkörpers. Des weiteren kann kinetische/thermische Energie der Moleküle
in elektromagnetische Energie umgewandelt werden, wenn die Moleküle untereinander
Stöße durchführen. Dies nennt man Emission.
Das Streuvermögen eines Teilchens hängt von seiner Größe, der geometrischen Form
und dem Brechungsindex ab. Daraus ergeben sich auch die Richtungsverteilung sowie die Extinktion. Wird ein sehr kleines Teilchen - im Vergleich zur Wellenlänge des
Lichts - getroffen, entsteht eine winkelabhängige Intensitätsverteilung für die die Einfallsrichtung der Strahlung eine Symmetrieachse bildet. Die gestreute Intensität ist in
Einfallsrichtung und entgegengesetzt dazu doppelt so groß wie für die dazu senkrechte Streuung. Es entsteht eine Intensitätsverteilung, für die die Ebene senkrecht zur
Einfallrichtung der Strahlung im Streuzentrum zusätzlich eine Symmetreiebene bildet. Dies nennt man Rayleigh-Streuung. Bei größer werdenden Teilchen verändert sich
16
KAPITEL 2. GRUNDLAGEN
das Streuverhalten. Sind die Teilchen nicht mehr klein gegenüber der Wellenlänge der
Strahlung, so wird die senkrechte Symmetrieebene aufgebrochen. Die Intensität der
Vorwärtsstreuung verstärkt sich mit wachsender Teilchengröße, wobei die Streuung in
rückwärtiger Richtung an Intensität verliert. Dies nennt man Mie-Streuung.
Abb. 2.3 Über Hornisgrinde (Schwarzwald) liegt eine feuchte Dunstschicht und darüber eine
löchrige Kumuluswolke (Cumulus fractus), durch die die Sonne sichtbar ist. Die Streuung an den
Wassertröpfchen der feuchten Atmosphäre dieses Ortes machte am 30.12.1997 die Lichtstrahlen
sichtbar.
2.3
Strahlungstransportgleichung
Strahlung verändert auf dem Weg durch die Atmosphäre seine Intensität. Diese Veränderung kann mit Hilfe der Strahlungstransportgleichung beschrieben werden. Dafür
wird ein isotropes Medium betrachtet, das sowohl absorbiet, emittiert als auch streut
und die Veränderung der Strahlungsintensität zwischen einfallender und austretender
Strahlung bestimmt. Bevor aber die Strahlungstransportgleichung erläutert werden
kann, müssen diese drei Prozesse näher beleuchtet werden. Zuerst betrachten wir den
Fall ohne Streuung.
Wir stellen uns vor, das Strahlung aus dem Frequenzintervall (ν, ν + dν) mit der
Strahldichte Iν in einem Raumwinkel dω normal auf eine Fläche dσ fällt. Dieses soll
in der Zeit dt stattfinden. Somit ist Iν dωdσdνdt die auf die Fläche einfallende Energie.
Der im Medium entlang der Strecke ds absorbierte Anteil ist βν,a dsIν dωdσdνdt wobei
βν,a der Absorptionskoeffizient für Strahlung der Frequenz ν ist.
Die emittierte Energie ist: ²ν dV dωdνdt. Dabei beschreibt der Emissionskoeffizient ²ν
die Energie, die von einem Volumenelement dV pro Zeit und Frequenz im Raumwinkel
dω abgestrahlt wird.
Mit dem Absorptions- und Emissionskoeffizienten ist nun eine Beschreibung des
Strahlungstransports, in einem nicht streuenden Medium, möglich. Man betrachtet
2.3. STRAHLUNGSTRANSPORTGLEICHUNG
17
Abb. 2.4 Darstellung der gedachten Figur ohne Streuung.
einen zylinderförmiges Volumen dV , dessen Grundfläche der bestrahlten Fläche dσ
und dessen Höhe der Wegstrecke ds entspricht. Die Strahlung der Intensität Iν fällt
senkrecht auf eine Grundfläche des Zylinders.
Die Differenz zwischen der oben einfallenden Intensität Iν und der unten austretender (Iν + dIν ) kann dadurch erklärt werden, dass innerhalb des Zylinders, entlang des
Weges ds Strahlung absorbiert wird, gleichzeitig aber der Zylinder Strahlung emittiert.
Dies kann wie folgt beschrieben werden:
(Iν + dIν )dωdσdνdt = Iν dωdσdνdt − βν,a dsIν dωdσdνdt + ²ν dV dωdνdt
(2.1)
Daraus erhält man die Änderung der Intensität:
dIν
= −βν,a Iν + ²ν
ds
(2.2)
Die Strahlungstransportgleichung (2.2) beschreibt die Veränderungen in der Intensität
der Strahlung auf ihrem Weg durch ein absorbierendes und strahlendes Medium. In
der Regel wird der Absorptionskoeffizient für eine Referenzwellenlänge angegeben und
nicht als Funktion der Frequenz. Betrachten wir daher den Fall βν,a = βa . Dann kann
(2.2) über die Frequenz integriert werden. Man erhält:
dI
= −βa I + ²
ds
mit ² =
R∞
0
²ν dν und I =
R∞
(2.3)
Iν dν.
0
Nun betrachten wir den Fall mit Streuung. Dafür ist es wichtig, die Einzelstreualbedo ω0 zu kennen. Diese gibt an, wie stark reflektierend bzw. absorbierend ein Teilchen
ist. Formal gesehen setzt sich die Einzelsteualbedo aus dem Verhältnis des Absorptionsund Extionktionskoeffitienden βext zusammen. Der Extinktionskoeffizient ergibt sich
aus der Summe von Absorptions- und Streukoeffizient βext = βa + βs
ω0 =
βs
βa + βs
(2.4)
18
KAPITEL 2. GRUNDLAGEN
• ω0 : Einzelstreualbedo
• βa : Absorptionskoeffizient
• βs : Streukoeffizient
Abb. 2.5 Darstellung der gedachten Figur mit Streuung.
Nun wird die Streufunktion χ(γ) eingeführt. Sie beschreibt die Wahrscheinlichkeit einer
Rückstreuung unter einem Winkel γ in einen festen Raumwinkel dω. Die Streufunktion
ist folgendermaßen normiert:
Z
dω
=1
(2.5)
4π
Damit sind wir in der Lage, die in einen Raumwinkel dω gestreute Energie zu
χ(γ)
bestimmen. βs Idω 0 ω0 χ(γ)dω/4π ist der aus einem Raumwinkel dω 0 kommende und
nach dω gestreute Anteil der Strahlung, wobei γ der Streuwinkel ist. Die gesamte in
einen Raumwinkel gestreute Energie pro Volumen, Zeit und Frequenz ist somit:
Z
dω
(2.6)
²dω = ω0 βs Iχ(γ)dω 0
4π
Nimmt man Streuung und Emission zusammen, erhält man als Strahlungskoeffizient:
Z
dω 0
+ ²0
(2.7)
² = ω0 βs Iχ(γ)
4π
²0 wird als Koeffizient der wirklichen Strahlung bezeichnet. Dies kann nun in die Strahlungstransportgleichung eingesezt werden.
dI
= −βa I + ω0 βs
ds
Z
Iχ(γ)
dω 0
+ ²0
4π
(2.8)
Die Strahlungstransportgleichung ist nur in sehr wenigen Spezialfällen analytisch zu
lösen. In den meisten Fällen wird zur Lösung auf numerische Verfahren zurückgegriffen.
Kapitel 3
Satelliten- und Modelldaten
In den letzten Jahrzehnten wurden zahlreiche unterschiedliche Satellitenmissionen
zur Fernerkundung von Wolken und Aerosolen gestartet. In der Praxis ist es meist jedoch schwierig, Messungen für einen Ort und Zeitpunkt von verschiedenen Messinstrumenten zu finden. Große Messkampagnen oder große Satelliten mit vielen Instrumenten
an Bord sollen dies ermöglichen. Die amerikanische Luft- und Raumfahrtbehörde hat
in Zusammenarbeit mit verschiedenen internationalen Instituten eine andere Variante realisiert: Der A-Train und weitere in meiner Arbeit verwendete Messgeräte und
Produkte sollen im Folgenden vorgestellt werden.
3.1
Meteosat Second Generation
Meteosat Second Generation (MSG) steht für eine Serie von europäischen geostationären meteorologisch genutzten Satelliten. Momentan ist der MSG 8 im operativen
Betrieb. Seine Position ist über dem Äquator und dem Nullten Längengrad in ca.
36.000 km Höhe. Sein Aufgabenbereich umfasst neben dem Nowcasting, dem Liefern
der Datenbasis für Wettervorhersagen, das Ermöglichen eines langfristigen Überblicks
und eine Energiebilanzierung durchzuführen. Das Messgerät SEVIRI (Spinning Enhanced Visible and Infrared Imager) an Bord von MSG hat zwölf Kanäle und einen
Messrhythmus von 15 Minuten. Davon messen neun Kanäle im infraroten und drei im
solaren Spektralbereich. Anhand von MSG-Messungnen lässt sich ein Überblick über
die zu untersuchende Region an der Westküste Afrikas bekommen.
19
20
KAPITEL 3. SATELLITEN- UND MODELLDATEN
3.2
A-Train
Der A-Train ist eine Formation aus sonnensynchronen, erdumlaufenden Satelliten.
Das A im Namen steht für afternoon, also den Nachmittag, was sich auf die lokale Äquatorüberflugzeit bezieht. Momentan fliegen fünf Satelliten im A-Train: Aqua und Aura
gehören zum Earth Observing System (EOS) der National Aeronautica and Space Administration (NASA), Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) ist eine Kooperation zwischen der NASA und dem französischen Centre
National d’Etudes Spatiales (CNES), der Polarisation & Anisotropy of Reflectances for
Atmospheric Sciences coupled with Observations from a Lidar (PARASOL) wird von
CNES und CloudSat von der NASA betrieben.Jeder dieser Satelliten hat einzigartige Messmöglichkeiten, die sich gegenseitig ergänzen. Deshalb ist es erstmals möglich
geworden, Wolken-, Aerosol-, Temperatur-, relative Feuchte- und Strahlungsflussmessungen nahezu gleichzeitig durchzuführen. Durch die Umlaufbahn der Satelliten wird
auch eine globale und saisonale Abdeckung gewährleistet. Wegen der kurzen zeitlichen
Abstände, zwischen den verschiedenen Messungen über einem Ort, kann man davon
ausgehen, dass keine gravierenden Änderungen im Umfeld des Messgebietes stattfinden.
3.2.1
CloudSat
Die Aufgabe von CloudSat besteht vor allem in
der Erstellung von Vertikalprofilen von Wolken mit
deren mikrophysikalischen Eigenschaften wie zum
Beispiel Teilchenkonzentration, Effektivradius und
Flüssigwassergehalt. Als Messinstrument fliegt auf
CloudSat ein 94-GHz Wolkenradar (CPR). CloudSat erstellt am Boden alle 1.1 km ein Profil. Dies
ist in 125 Schichten eingeteilt mit einer vertikalen
Auflösung von 240 m. Während einem Orbit werden
somit 36.383 Profile erstellt. Die Teilchenkonzentration der Wolken ist ein Bestandteil des cloud water
content Produktes von CloudSat. Die Teilchenkonzentration wird für die Berechnung des Flüssigwasser von Wolken benötigt.
Abb. 3.1 CloudSat
3.2. A-TRAIN
21
Gemessen wird das Rückstreuprofil, aus dem dann die weiteren Produkte entstehen
(geometrisches Wolkenprofil, Wolkenklassifikation, Wassergehalt der Wolke, Eisgehalt
der Wolke, wolkenoptische Dicke, Strahlungsflüsse und Heizraten). Teilweise werden
zur Erstellung der Produkte Daten des Moderate Resolution Imaging Spectrometers
(MODIS) hinzugezogen. Alle Level 1 und 2 Standardprodukte sind auf einem hierarchischen Schema aufgebaut. Um ein Produkt zu generieren, werden immer die Parameter
des vorherigen Produkts benötigt. Wenn ein Messfehler auftritt oder einer der ersten
Parameter fehlerbehaftet ist, setzt sich dies in den weiteren Produkten fort. Dieses Verfahren wird zudem konservativ betrieben, was zu großen Datenlücken führt. Weiterhin
hat das CloudSat Radar große Schwierigkeiten mit Bodenreflektanzen. Die Messungen
der unteren 1.5 km sind daher nur teilweise zur Auswertung geeignet.
3.2.2
CALIPSO
CALIPSO fliegt an dritter Position im A-Train mit
15 Sek. Abstand zu CloudSat und ca. 2 min 45 Sek.
zu Aqua. Das Cloud-Aerosol LIdar with Orthogonal Polarisation (CALIOP) ist das wichtigste Instrument an
Bord. Die CALIPSO Mission wurde entwickelt um den
direkten und indirekten Einfluss von Aerosolen auf den
Strahlungshaushalt zu bestimmen und die Charakterisierungen des langwelligen Strahlungsflusses und der atmosphärischen Heizraten zu erfassen und eine Verbes-
Abb. 3.2 CALIPSO
serung in den Modell-Parametrisierungen der WolkenKlima-Kopplung zu erreichen. Die Messungen des CALIPSO Satelliten werden hier vor allem zur Bestimmung
der Aerosole genutzt.
22
KAPITEL 3. SATELLITEN- UND MODELLDATEN
3.2.3
MODIS
Das Moderate Resolution Imaging Spectroradiometer
(MODIS) ist das Hauptinstrument auf den NASA Satelliten Aqua und Terra. MODIS hat 36 spektrale Kanäle,
die zwischen 0.4 und 14.4 µm eingeteilt sind. Zwei der
Kanäle haben eine Auflösung von 250 m im Nadir, weitere fünf haben eine 500 m Auflösung und die restlichen 29
Kanäle haben eine 1 km Auflösung. MODIS liefert viele
Abb. 3.3 MODIS
verschiedene Produkte für Aerosole, Wolken und Landbzw. Wasseroberflächen.
Die fertigen Datenprodukte bestehen aus einer Kombination von Parametern, die
aus Messungen im infraroten und solaren Spektralbereich abgeleitet werden. Das MOD06Produkt gibt physikalische und strahlungsbezogene Eigenschaften der Wolke wieder.
Es liefert zum Beispiel Daten über den effektiven Partikelradius, die wolkenoptische
Dicke und die effektive Emissivität. Die optische Dicke von MODIS wird später mit
der errechneten optischen Dicke des CloudSat Produktes verglichen.
3.3
OPAC
Wolken und Aerosole haben sehr variable Eigenschaften. In den meisten Fällen sind
die genauen Parameter von Wolken und Aerosolen wie die Teilchenanzahl und Teilchendichte, der spektrale Brechungsindex und die Form aber auch die Größenverteilung
unbekannt. Es ist aus diesen Gründen unmöglich, exakte Modellierungen von Wolken
und Aerosolen durchzuführen. Der OPAC Datensatz beinhaltet eine Beschreibung der
typischsten Fälle von Wolken und Aerosolen und liefert gleichzeitig ein Software-Paket,
das die Berechnung der optischen Eigenschaften für jede Mischung der Aerosole und
Wolken möglich macht. Es werden verschiedene optische Eigenschaften für zwei StratusWolken (’kontinental’, ’maritim’), drei Cumulus-Wolken (’kontinental sauber’, ’kontinental verschmutzt’, ’maritim’), für Nebel und drei verschiedene Zirrus-Wolken geliefert. Als fertig gemischte Aerosole werden drei kontinentale (’sauber’, ’durchschnittlich’
und ’verschmutzt’), ein urbanes Aerosol, ein Wüstenaerosol, drei maritime Aerosole
(’sauber’, ’verschmutzt’ und ’tropisch’) sowie ein arktisches und ein antarktisches Aerosol aufgeführt. Diese setzen sich dann aus den verschiedenen Bestandteilen wie Ruß,
Meersalz, verschiedenen Mineralien und Sulfat zusammen. Es werden Parameter für
3.4. GFS
23
die Wasserlöslichkeit und die Stärke der Unlösbarkeit angegeben. Außerdem kann zwischen acht verschiedenen Feuchtegehalten für die Aerosole gewählt werden.
Das betrachtete Aerosol entsteht bei der Verbrennung von Biomasse und hat einen
hohen Rußanteil. Da es im OPAC Datensatz kein biomass burning aerosol gibt, wurde
ein urbanes Aerosol gewählt. Es hat den größten Anteil an Ruß und ist dem biomass
burning aerosol somit am ähnlichsten. Die Zusammensetzung des urbanen Aerosols ist
in Tabelle 3.1 aufgelistet. Aufgeführt werden die Teilchenkonzentration N, die Massenkonzentration M, die Mixrate der Teilchen, die Massen Mixrate sowie der modale
Radius der logarithmischen Normalverteilung für die Telichenverteilung rmod,N .
Komponente
N [cm3 ]
M [µgm− 3]
Mixrate
Massen
rmod,N [µ m]
der Teilchen Mixrate
Wasser löslich
unlöslich
Ruß
28.000
56.0
0.177
0.563
0.0212
1.5
35.6
−
0.99E 5
0.358
0.471
130.000
7.8
0.823
0.079
0.0118
Tabelle 3.1 Zusammensetzung des urbanen Aerosols aus OPAC
Die Einfachstreualbedo ω0 ist für das urbane Aerosol mit 0.817 bei 0.55 µm angegeben und hat damit den kleinsten Wert von allen aufgeführten Aerosoltypen. Dies
bedeutet, dass das Aerosol nicht nur reflektierende sondern auch absorbierende Eigenschaften aufweist. Das urbane Aerosol hebt sich darurch hervor, dass es sehr viel stärker
absorbiert, aĺs andere Aerosole. So habt ein maritimes Aerosol eine Einzelstreualbedo
von 0.997 oder ein durchschnittliches kontinentales Aerosol eine Einzelstreualbedo von
0.925 jeweils bei 0.55 µm.
3.4
GFS
Das von NOAA betriebene Global Forecast System (GFS) produziert vier mal täglich Vorhersagen für die nächsten 348 Stunden. Dabei hat es eine horizontale Auflösung
von 70 km. Vertikal ist es in 64 Schichten aufgeteilt und endet bei einer Höhe von 0.2
hPa. In das Modell ist ein See-Eis-Modell und ein Land-Modell mit eingebaut.
24
KAPITEL 3. SATELLITEN- UND MODELLDATEN
In dieser Arbeit werden Vorhersagewerte für die Feuchtigkeitsverteilung in den verschiedenen Höhenschichten verwendet, um eine Abschätzung für die relative Luftfeuchte und die relative Feuchte der Aerosolschicht für die Strahlungstransportrechnungen
durchführen zu können. Vorhersagen für die vertikale Temperatur- und Druckverteilung
werden zur Berechnung der lokalen Dichte in Höhe der Aerosolschicht herangezogen.
3.5
Strahlungstransportmodell MOMO
Die Urform des Strahlungstransportmodells MOMO wurde im Jahr 1984 von Prof.
J. Fischer und Prof. H. Graßl entwickelt. Es basiert auf der Matrix-Operator-Methode
(MO-Methode). Diese ist besonders gut für Berechnungen des Strahlungstransportes
in planparallel geschichteten Medien mit hoher optischer Dicke geeignet. Der Aufbau
der Atmosphäre wird durch frei wählbare vertikale Schichten realisiert. Die einzelnen
Schichten müssen sowohl vertikal als auch horizontal homogen sein. Der Aufbau über
ein Schichtsystem macht es möglich, verschiedene optische Eigenschaften miteinander
zu kombinieren. Diese homogenen Schichten werden für die Berechnung des Strahlungstransports in so dünne Unterschichten eingeteilt, dass sich für jede Schicht die Streuung
durch den Einfachstreuansatz approximieren lässt. Diese werden dann mit dem doubling-Algorithmus für optisch identische Schichten bzw. mit dem adding-Algorithmus
für optisch unterschiedliche Schichten zu einer Atmosphäre zusammen gesetzt. So kann
man mehrere Wolkenschichten oder auch Wolken- und Aerosolschichten übereinander
anordnen. Im Gegensatz zur Monte-Carlo-Methode – bei welcher der Weg jedes einzelnen Photons durch die Atmosphäre durch Zufallsgrößen bestimmt wird – sind bei
der MO-Methode die Reflexions-, Transmissions- und Quellfunktionen für jede Schicht
bekannt. Sie müssen zwar auch berechnet werden, aber dieser Weg ist effektiver, was
zu einem geringeren Rechenaufwand führt. Die Daten für Wolken- und Aerosoleigenschaften werden aus dem OPAC Datensatz entnommen.
Die beiden Randbedingungen werden durch die solare Einstrahlung und die Bodenbeschaffenheit in das Modell eingebracht. Land bzw. Ozean werden durch eine entsprechend reflektierende Fläche dargestellt. Die solare Einstrahlung kann für die jeweiligen
Berechnungen als räumlich und zeitlich konstant angesehen werden und ist nur noch
vom betrachteten Wellenlängenintervall abhängig. Der so berechnete aufwärtsgerichtere Strahlungsfluss muss nun über den Wellenlängenbereich integriert werden. Die
Integration wurde mit Hilfe eines von Dr. Anja Hühnerbein geschreibenen Programms
3.6. WOLKEN
25
durchgeführt und dann mit der Solarkonstante des betrachteten Wellenlängenbereich
auf Ein normiert. Um die jahreszeitlichen Änderungen in der Einstrahlung mit einzubeziehne, können die Ergebnisse mit der aktuellen Solarkonstante multipliziert werden,
um die Werte mit Messergebnissen vergleichen zu können.
Abb. 3.4 Dargestellt ist die Intervallgröße der Wellenlängen.
3.6
Wolken
Wolken haben einen starken Einfluss auf
die Albedo der Erde. Dieser macht sich vor
allem bei dunklen Untergründen wie Wasser bemerkbar. Die Wolken werden anhand
eines 1956 von der WMO herausgegebenen Wolkenatlas klassifiziert. Dieser gibt eine erste grobe Einteilung nach der Höhe
der Wolkenuntergrenze über dem Erdboden. Die für die Simulationen asugewählte
Wolkenart, gehört zu den tiefen Wolken, die
ihre Untergrenze zwischen 500 m und 2000
m haben.
Abb. 3.5 Die Aufnahme zeigt einen fast
durchsichtigen, schichtförmigen Stratokumulus
(Stratocumulus stratifomis perlucidus) am Abend
über Lorch (Baden-Württemberg).
Die gezeigte Wolke ist ein Stratokumulus (Haufenschichtwolke). Grenzschichtwolken, zu welchen diese gehören, bedecken große Teile der Ozeane. In Gebieten mit starken
26
KAPITEL 3. SATELLITEN- UND MODELLDATEN
Inversionen sind sie fast das ganze Jahr über zu finden. Die ausgedehnten Wolkenfelder
reflektieren ca. 30% der solaren Einstrahlung und sind somit klimarelevant. Sie können
als dünne Schicht oder als Anordnung von Haufen auftreten, welche die Sonne nur
schwach, manchmal aber auch deutlich durchblicken lassen. Der Stratokumulus ist eine
Wasserwolke und bringt im allgemeinen keinen Regen. Da die Parametrisierung von
Wolken im Allgemeinen sehr schwierig ist, wird im Folgenden auf den Spezialfall des
adiabatisch geschichteten Plan-Parallelen Modells (AS-PPM) für die Stratokumulsbewölkung beziehen. Dieses Modell wurde von der Groupe de Meteorologie Experimentale
et Instrumentale (GMEI), des Centre National de Recherches Meteorologiques (CNRM)
und dem französischen Wetterdienst Meteo-France entwickelt.
In dem adiabatisch geschichteten Plan-Parallelen Modell, das hier zur Anwendung kommt, werden die sich verändernden mikrophysikalischen Eigenschaften eines
konvektiven Paketes feuchter Luft beschrieben. Die Wolke ist am Unterrand in ihrem Wasserdampf-Mischungsverhältnis gesättigt. Während eines konvektiven Aufstiegs
kühlt sich das Luftpaket dem pseudo-adiabatischen Temperaturgradienten folgend ab
und der Sättigungsdruck sinkt entsprechend der Temperatur. Mit dem feucht-adiabatischen
Kondensationskoeffizienten Kad lässt dich der adiabatische Flüssigwassergehalt LW Cad
in der Höhe h über der Wolkenbasis bestimmen.
LW Cad (h) = Kad ∗ h
(3.1)
Der LW Cad (h) ist als die Differenz des Sättigungsmischungsverhältnis der Wolkenuntergrenze und des betrachteten Niveaus h definiert und steigt nahezu linear mit der
Höhe an. Der feucht-adiabatische Kondensationskoeffizient hingegen ist Höhenkonstant
für kleine Höhenunterschiede. Dies trifft zum Beispile auf typische Stratokumulusbewöklung zu (Schüller, 2000)
Die einfachste Beschreibung der optischen Dicke einer Wolke erfolgt als Produkt
ihrer geometrischen Höhe H und des Extinktionskoeffizienten σext .
τ = σext H
(3.2)
Daraus kann man dann mit Hilfe der Beschreibung des Extinktionskoeffizienten von
R∞
σext = πr2 Qext n(r)dr, wobei n(r) die Verteilungsfunktion der Tröpfchengrößen und
0
Qext der Wirkungsgrad der Extinktion ist – der zwar wellenlängenabhängig ist, aber
für die hier verwendete Referenzwellenlänge von 550 nm gegen Zwei strebt – folgt für
ein adiabatisches Modell:
τ = 2HNad πre2
(3.3)
3.6. WOLKEN
27
Die adiabatische Tropfenkonzentration Nad ist für ein adiabatisches Luftpaket ohne
Niederschlag konstant und kann zum Beispiel mit CloudSat gemessen werden. Um
das Modell auch ohne den Effektivradius re , dessen Messung durch die vorhandenen
Aerosole verfälscht wird, beschreiben zu können, zieht man das Verhältnis k aus Effektivradius r und dem volumengewichteten Mittelwert der Verteilung rv = (r¯3 )−1/3
heran.
Kad 1/3 −1/3
h) Nad
rad (h) = k −1/3 rv,ad = ( 4
πρω
3
(3.4)
1
5
Kad 2
3
τ = πQext ( 4
) 3 (kNad ) 3 H 3
5
πρω
3
(3.5)
Hier ist nun τ nicht mehr proportional zu H sondern zu H 5/3 . Damit beeinflusst die
geometrische Dicke einer adiabatischen Wolke im Plan-Parallelen Modell die Strahlungseigenschaften erheblich. Innerhalb der MOMO Reschnungen werden die optischen
Dicken mit Hilfe der mikrophysikalischen Eigenschaften berechnet. Für die Berechnung
der optischen Dicke aus CloudSat und CALIPSO Messungen wurde aber die Formel
3.5 herangezogen. Damit ist es möglich die optische Dicke auch ohne Kenntnis des
Effektivradius zu berechnen.
28
KAPITEL 3. SATELLITEN- UND MODELLDATEN
Kapitel 4
Simulationen
Aerosole können einen starken Einfluss auf das Niederschlagsverhalten der Wolken
aufweisen. In Afrika zeigt sich dies besonders im Frühjahr zu Beginn der Regenzeit.
Die Aerosole stellen zusätzliche Kondensationskerne dar. Wird die Anzahl der Kondensationskerne erhöht, so steigt auch die Teilchenkonzentration in der Wolke und der
effektive Teilchenradius wird verringert. Die Lebensdauer der Wolken verlängert sich,
da ein Abregnen nur bei genügend großen und somit schweren Tröpfchen stattfinden
kann. Man hat festgestellt, dass die Intensitäten der afrikanischen Feuer stark mit den
vorangegangenen Regenzeiten korrellieren. Das Jahr 1992 beispielsweise war in Afrika
recht trocken. Der Kontinent befand sich im Einflussgebiet des El Niño Phänomens.
Während eines El Niño Jahres ist es in Afrika trockener, während eines La Niña Jahres
feuchter als im Normalfall. In Jahren mit El Niño Einfluss ist auch die Vegetation nur
gering. Die Feuer haben kaum Nährstoffe, bleiben kleiner und sind seltener. Umgekehrt ist der Einfluss ebenso zu spüren. Die Ausbreitung der Freuer hängt also von der
Menge an vorhandenen Biomasse ab. Ist viel Biomasse vorhanden, so können sich die
Feuer gut ausbreiten und es werden viele Aerosole in die Atmosphäre eingetragen. Die
so erhöhte Zahl an Kondensationskernen verlängert die Lebensdauer der Wolken und
kann eine Minderung der Regenmenge bewirken (Swap et al., 2003)
In dieser Arbeit wurde eine Sensitivitätsstudie durchgeführt, die anhand einer Fallstudie aus CALIPSO, CloudSat und MODIS Messungen - die mir von Damien Josset
vom Service d’Aeronomie-IPSL, Universite Paris 6 als fertiges Produkt zur Verfügung
gestellt wurden - aufgebaut wurde. Die Fallstudie sowie die restliche Eingangsdaten für
die Sensitivitätsstudie werden im folgenden Abschnitt ausführlich beschrieben. Bei der
Fallstudie handelt es sich um eine Messung vom 13. August 2006 im Golf von Guinea.
Hier wurde eine Aerosolschicht festgestellt, die sich teilweise über einer Stratokumuluswolke befindet. Diese Messung wurde von CALIPSO um 13.40UTC aufgenommen
29
30
KAPITEL 4. SIMULATIONEN
Diese Abbildung zeigt einen ersten Blick auf eine CALIPSO Messung. Auf der Ordinate ist
die geometrische Höhe eingetragen, die Abzisse zeigt die Breitengrade des Überfluges am 13.
August 2006 an. Die breite rot-gelbe Linie zeigt
eine Wolkenschicht zwischen den Breiten -8° bis
-25°. Zwischen 0° und -8° ist keine Wolke gemessen worden. Die Wolke befindet sich in ca.
1.2 km Höhe. Über die gesamte Breite der Messung ist eine Aerosolschicht zu erkennen (hier
Abb. 4.1 CALIPSO quicklook für den
13.08.2006
in einer Gelbschattierung eingetragen). Diese
Schicht liegt in einer Höhe von 2 bis 5 km.
Passend zu der vorangegangenen Abbildung
wird hier die optische Dicke der gemessenen Aerosolschicht gezeigt. Diese ist für den wolkenlosen Bereich aus einer Kombination aus MODIS
und CALIPSO Messungen, für den Bereich mit
Wolke ausschließlich aus CALIPSO Messungen
erstellt worden. Die Werte schwanken für die
Fallstudie um eine optische Dicke von 1, allgemein können aber auch Werte zwischen 0 und
Abb. 4.2 Optische Dicke des Aerosols
2.5 annehmen. Die zwei schwarzen senkrechten
Linien markieren die zwei Fallstudien, die betrachtet werden sollen.
Das gemessene Aerosol wird als black carbon, also Kohlenstoff-Aerosol beschrieben. Es ist stark rußhaltig und wird den biomass burning aerosols zugeordnet. Die
beiden in der letzten Abbildung gekennzeichneten Fälle haben folgende Grunddaten:
Ort der Messung
Fall 1
Fall 2
6.00°S, 1.12°O
8.06°S, 1.58°O
Wolkenuntergrenze
1.21 km
Wolkenobergrenze
1.41 km
Aerosoluntergrenze
2.13 km
2.25 km
Aerosolobergrenze
3.24 km
4.29 km
optische Dicke des Aerosols
0.9
1.1
Tabelle 4.1 Grunddaten der Fallstudien
31
Abb. 4.3 Das Schema zeigt den strukturellen Aufbau der Modellatmosphäre. Es befindet sich eine
Aerosolschicht über den Ozean. Zwischen Ozean und Aerosolschicht kann sich eine Wolkenschicht
aus Stratokumuluswolken befinden. Simuliert wird der gesamte solare Strahlungsfluss am Oberrand
der Atmosphäre.
Für die Simulationen mit den Strahlungstransportmodell MOMO wurde eine tropische Modellatmosphäre angenommen, da sich der Ort der Fallstudie in den Tropen
befindet (6-8° südlich des Äquators). Der Aufbau der Atmosphäre für die Simulationen
basiert auf den Daten von Fall 2 der Fallstudie. Im weiteren Verlauf der Arbeit ist
mit Fallstudie immer der Fall 2 der von Damien Josset gemachten Messungen gemeint.
Oberhalb des Ozeans, dessen Albedo auf 0.02 festgesetzt wurde, ist eine Wolkenschicht
zwischen 1.2 km und 1.4 km und eine Aerosolschicht in der Höhenschicht zwischen 2.2
km und 4.3 km zu erkennen. Die optischen Dicken der Wolke und des Aerosols sind variabel. Die Berechnungen wurden für vier optische Dicken der Wolkenschicht und zehn
optische Dicken der Aerosolschicht durchgeführt. Die Strahlungsflusssimulationen wurden für alle Kombinationen der optischen Dicken durchgeführt. In Tabelle 4.2 werden
die ausgewählten otischen Dicken für Wolken- und Aerosolschicht aufgeführt.
optische Dicke der Wolke
optische Dicke des Aerosols
0, 3, 10, 30
0, 0.5, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.5
Tabelle 4.2 Optische Dicken von Wolken- und Aerosolschicht für die Simulationen
Diese Grunddaten wurden nun mit den Eigenschaften des urbanen Aerosols aus der
OPAC Datenbank in das Strahlungstransportmodell MOMO eingespeist. Berechnet
wurde der solare Bereich zwischen 200 nm und 3650 nm, der in 184 Intervalle eingeteilt wurde. Diese Intervalle sind in Bereichen mit starken Absorptionsbanden und
starker solarer Intensität sehr klein (< 2 nm) können aber auch Größen von über 100
nm haben. Für die Mischung des Aerosols kann man verschiedene Feuchtegehalte angeben. Der Ort der Fallstudie befindet sich in tropischen Regionen über dem Ozean,
32
KAPITEL 4. SIMULATIONEN
deshalb ist eine relativ hohe Luftfeuchte zu erwarten. Um einen möglichst genauen
Wert zu erhalten, wurden Vorhersagen des globalen Vorhersagemodells des amerikanischen Wetterdienstes (GFS) für den 13. August 2006 herangezogen. Im Lauf der 12
Uhr-Vorhersage wurden für die Höhenschichten, in denen sich Aerosol und Wolke befinden, relative Feuchten mit einem Mittelwert von 78% vorhergesagt. Die Simulationen
wurden mit einer relativen Feuchte von 80% durchgeführt, das bei einer Standardabweichung der relativen Feuchte von 9% gut im Fehlerintervall liegt.
Ein Experiment des U.S. Forest Service Fire Science Laborarory (FSL Missoula,
MT) hat gezeigt, dass die Einzelstreualbedo von biomass burning aerosols stark variieren kann. Über das bei der Fallstudie gemessene Aerosol war nur bekannt, dass
es Kohlenstoffhaltig ist. Es gab keine näheren Angaben zur Zusammensetzung des
Aerosols. Deshalb wurde aus dem OPAC-Datensatz das Aerosol mit dem größten Kohlenstoffanteil ausgewählt, um das gemessene Aerosol der Fallstudie zu simulieren. Die
Einzelstreualbedo des urbanen Aerosols wird bei einer Referenzwellenlänge von 0.55
µm mit 0.817 angegeben. In Abbildung 5.3 ist der spektrale Verlauf der Einzelstreualbedo des urbanen Aerosols abgebildet. Mit der chemischen Zusammensetzung ändert sich aber auch die Einzelstreualbedo eines Aersolos, weshalb die Simulationen
zusätzlich mit veränderten Absorptionskoeffizient βa (siehe Formel 3.1), der um 5%
bzw. 10% verringert wurde, durchgeführt wurden. Die Summe aus Absorptionskoeffizient und Streukoeffizient wurde dabei konstant gehalten. Für biomass burning aerosols
kann die Einzelstreualbedo, je nach Brennmaterial und Brennvorgang Werte zwischen
0.394 und 0.939 bei einer Wellenlänge von 532 nm annehmen (Hopkins et al., 2007).
Die Variabilität der Eigenschaften von Aerosolen ist sehr groß und somit nicht umfassend modellierbar, deshalb sollen die Ergebnisse der Berechnungen dieser Variation
nur einen Trend anzeigen. Da die Einzelstreualbedo momentan noch nicht mit Fernerkundungsverfahren nicht messbar ist, wären in situ Messungen zur Ergänzung der
Eingangsdaten wichtig. Damit könnten notwendige Annahmen mit Messdaten belegt
werden. Die Einzelstreualbedo oder deren spektraler Verlauf sind momentan mit Fernerkundungsverfahren nicht messbar. Gerade deshalb fehlen auch in situ Messungen.
Um die getroffene Annahme eines urbanen Aerosols zu erweitern und die Variabilität
der Einzelstreualbeden mit zu berücksichtigen wurden die Variationen des Absorptionskoeffizienten durchgeführt.
Das Strahlungstransportmodell MOMO berechnet den auf- und abwärts gerichteten Strahlungsfluss, sowie die Strahldichten an allen Schichtgerenzen. Für diese Arbeit
ist der aufwärts gerichtete Strahlungsfluss am Oberrand der Atmosphäre relevant. Die
33
Werte werden für die einzelnen Wellenlängenintervalle separat ausgegeben. Diese wurden mit der solaren Einstrahlung gewichtet aufsummiert und danach auf eine Solarkonstante von 1 normiert. Berechnet wird somit der Anteil der solaren Strahlung, der nach
dem Durchlaufen der Erdatmosphäre wieder an ihrem Oberrand austritt. Die Werte
für den normierten Strahlungsfluss können dann mit den aktuellen Werten der Solarkonstanten multipliziert werden, um die Änderungen des Strahlungsflusses in W/m2
zu erhalten. Diese kann auch in Erwärmungsraten pro Tag umgerechnet werden.
34
KAPITEL 4. SIMULATIONEN
Kapitel 5
Ergebnisse
Zu Beginn dieses Kapitels wird ein Überblick über die typische Wolkensituation im
Golf von Guinea gegeben. Dann wird gezeigt, aus welchem Gebiet die betrachteten Aerosole mit hoher Wahrscheinlichkeit stammen. Außerdem werden zusätzliche Messdaten
für die Fallstudie aufgeführt, bevor die Ergebnissen und deren Diskussion dargestellt
werden. Zusätzliche Grafiken der Ergebnisse sind im Anhang zu finden.
5.1
Messdaten
Aus CALIPSO-Messungen sind die geometrische Dicke der Wolken- sowie der Aerosolschicht und die aerosoloptische Dicke bekannt. Die optische Dicke der Wolken ist
allerdings unbekannt, da die Aeroslosschicht eine Messung der wolkenoptischen Dicke
verhindert. Die optische Dicke der Wolkenschicht hat aber einen starken Einfluss auf
die Strahlungsbilanz. Diese möglichst genau zu kennen ist somit wichtig für eine gute
Abschätzung des Einflusses der Aerosolschicht auf den Strahlungshaushalt.
In dem betrachteten Gebiet, im Golf von Guinea, ist fast jeden Tag eine Stratokumulusbewölkung zu finden. Das liegt an den dort vorherrschenden Bedingungen: An der
afrikanischen Westküste zieht sich der kalte Benguelastrom von Süden nach Norden,
was zu einer tief liegenden Grenzschicht (1 bis 2 km) führt. Der Einfluss des großräumigen Hochdruckgebietes über dem südlichen Atlantik und die damit verbundene
Absinkbewegung lässt nur noch eine Entstehung von Hochnebelfeldern, Stratokumulusbewölkung oder Stratusfeldern zu. Diese sehr konstanten Bedingungen, die man auch
vor der Westküste Süd-Amerikas vorfindet, sind für Forschungsarbeiten gut geeignet.
Einen guten Überblick über diese Region kann man sich auch mit dem geostationären
Satelliten MSG (Meteosat Second Generation) verschaffen. Aus technischen Gründen
35
36
KAPITEL 5. ERGEBNISSE
liegen für den Tag meiner Fallstudie leider keine Daten des MSG bereit.Die folgenden
Abbildung sind dennoch interessant, da die Bedingungen sehr konstant sind. Sie zeigen
eine typische Wolkensituation an der afrikanischen Westküste. Da die Aufnahmen nur
einen Tag nach der Fallstudie aufgenommen wurden, kann vermutet werden, dass es
sich um die gleiche Wolkengruppe handelt, die auch am Vortag beobachtet wurde.
b
a
Abb. 5.1 Abbildungen a und b sind MSG-Aufnahmen vom 14. Aug. 2006. Abb. a zeigt eine
typische Wolkensituation im Golf von Guinea. Es ist ein so genanntes rgb, das die Wolken und die
Meeresoberfläche durch Kombination der spektralen Kanäle als Kombination von rot, grün und blau
darstellt. Dies ist ein Produkt, das am Institut für Weltraumwissenschaften (ISS) an der FU-Berlin
entwickelt wurde. Ein weiteres Produkt, dass am ISS entwickelt wurde, ist das Druckfeld der
Wolkenoberkannten aus MSG-Messungen (Abb. b). Die orangen Werte von ca. 850 hPa stellen tiefe
Stratokumuluswolken dar. Wolken, die kleinere Werte aufweisen (gelb bis grün) sind
dementsprechend hochreichend in ihrer Struktur. In grau sind wolkenlosen Gebiete dargestellt.
5.2
Ursprung der Aerosole
Woher aber kommen die Aerosole? Kann davon ausgegangen werden, dass es sich um
biomiss burning aerosols handelt? Um eine Idee über das Ursprungsgebiet der Aerosole zu bekommen, wurden Rüchwärtstrajektorien für diesen Tag in drei verschiedenen
Höhen (auf der Internetseite der NOAA (National Oceanic and Atmospheric Administration)) berechnet. Für die Berechnungen wurde das Hysplit Modell der NOAA
verwendet (Spring,2008). Diese sind in der folgenden Abbildung gezeigt. Für die Rück-
5.2. URSPRUNG DER AEROSOLE
37
wärtstrajektorien ist als Startpunkt der Ort der Fallstudie gewählt worden. Die Läufe
zeigen die mit dem GDAS (Global Data Assimilation System) gerechneten Trajektorien für die letzten 148 h. Es sind drei Trajektonien, je eine für die Höhen 1500 m, 2500
m und 3500 m, berechnet worden.
Abb. 5.2 Rüchwärtstrajektorien für die Höhen 1.5 km, 2.5 km und 3.5 km für Ort und Zeit der
Fallstudie 2.
38
KAPITEL 5. ERGEBNISSE
Abb. 5.3 Mit MODIS registrierte Feuer zwischen dem 9. und dem 18. August 2006.
Gut zu sehen ist, dass alle Trajektorien ihren Ursprung über dem afrikanischen
Festland haben. Die rote und die blaue Trajektorie stammen aus einem Gebiet um das
Kongobecken in Zaire. Sie haben dort eine geometrische Höhe von über 5000 m, was
auf ein sehr warmes Festland schließen lässt. Auf ihrem Weg zu dem Messpunkt der
Fallstudie verlieren sie langsam an Höhe. Die grüne Trajektorie hat ihren Ursprung
über dem Adamaoua-Gebirge in Kamerun.
Schaut man sich dazu die nächste Abbildung an, so kann man feststellen, dass die
Aerosole aus einem Gebiet mit einer Vielzahl von registrierten Bränden kommen. Die
Grafik zeigt alle Feuer, die zwischen dem 9. und dem 18. August 2006 mit MODIS
auf Terra und Aqua gemessen wurden. Jeder rote Punkt steht für mindestens einen
Brandherd in der 10-Tage-Periode. In den gelb markierten Regionen ist die Anzahl
der regestrierten Brände hoch. Die rote und die blaue Trajektorie stammen also aus
Gebieten, in denen in diesem Zeitraum mehrere Brände festgestellt wurden. Die Höhenangabe für die Urspungsgebiete liegt bei über 5 km Höhe.
Aber warum befinden sich der Ursprung der Aerosole in fast 5 km Höhe und weshalb kann man die Aerosole, über dem Ozean, oberhalb von Wolken vorfinden? Um
diese Frage bantworten zu können, muss man wissen, dass das Einbringen der Aerosole bei Feuern normalerweise innerhalb der Grenzschicht geschieht (Labonne et al.,
2007). Deren Oberkannte liegt im Durchschnitt über dem südlichen Afrika in einer Höhe zwischen 3 und 4.5 km. Die Aerosole werden also in die Grenzschicht eingebracht
5.3. WOLKENOPTISCHE DICKE
39
und von dort mit den Winden in andere Gebiete transportiert. Liegt die Oberkannte
der Grenzschicht in diesen Gebieten unterhalb der Höhe, in denen die Aerosole in die
Grenzschicht gelangten, so können die Aerosole oberhalb der Grenzschicht angetroffen
werden. Über dem kalten Benguelastrom variiert die Höhe der Grenzschichtoberkante zwischen 1 und 2 km. Es ist somit ein typischer Fall, dass hier die Aerosolschicht
oberhalb der Stratokumulusfelder vorgefunden wird.
5.3
Wolkenoptische Dicke
Wie bereits beschrieben, ist die Kenntniss der wolkenoptischen Dicke wichtig für
die Abschätzung des direkten Aerosoleinflusses auf den Strahlungshaushalt. Um die
optische Dicke der in der Fallstudie gesehenen Wolken zu erhalten, wird angenommen,
dass es sich bei dem betrachteten Stratokumulus um eine adiabatisch geschichtete
plan-parallele Wolke handelt. Dann kann über die Gleichung (12) die optische Dicke
der Wolke berechnet werden, wenn man die Teilchenkonzentration kennt. Das Wolkenradar von CloudSat bietet ein solches Produkt. Die betrachteten Wolken befinden sich
aber innerhalb der unteren zwei Kilometer der Atmosphäre. Es ist bekannt, dass die
Datenprodukte von CloudSat in den unteren eineinhalb Kilometern mit Bodenreflektionen Probleme haben. Deshalb tauchen hier häufig Datenlücken auf. Für unseren Fall
der Messung am 13. August 2006 sind diese Datenlücken nur sehr dünne Streifen in
einer sonst guten Messung.
Abb. 5.4
Dies ist eine Aufnahme der Wolkenmaske von MODIS auf Aqua für den 13. Aug. 2006.
Die Pfeile zeigen die zwei Orte der angeführten Fallstudien an.
In einer Auswertung der Teilchenkonzentration der ersten zweieinhalb Jahre MO-
40
KAPITEL 5. ERGEBNISSE
Abb. 5.5 Diese Abbildung stellt die von CloudSat gemessene Teilchenkonzentration in der
Stratokumuluswolke dar. Die Teilchenkonzentration ist in Teilchen/cm3 angegeben. Für die
Fallstudie erhält man mit einer Mittlung über die Vertikalverteilung, einen Wert von 80
Teilchen/cm3 .
DIS Messungen (Bennartz, 2007) wurde gezeigt, dass für das Gebiet des südlichen
Atlantiks die durchschnittlichen Werte zwischen 40 und 60 Teilchen pro cm3 liegen.
Betrachtet man aber die Einzelfälle, so können Werte von 200/cm3 erreicht werden.
Dies geschah immer dann, wenn der Einfluss der afrikanischen Waldbrandsaison sehr
groß war. Die von CloudSat gemessenen Werte von ca. 80/cm3 sind also nicht besonders
hoch, da wir uns in der Waldbrandsaison befinden. Mit diesem Wert erhält man eine
optische Dicke von 14.5 zur Überprüfung der Simulationen. Das Wolkenprodukt von
MODIS liefert eine optische Dicke von 8.76 für den gleichen Ort bei einem zeitlichen
Unterschied von weniger als zwei Minuten. Die zeitliche Differenz in den Messungen
ist zu vernachlässigen, da stabile Bedingungnen für die Wolke herrschen. Jedoch ist
zu betachten, dass MODIS die Aerosloschicht oberhalb der Wolke nicht erkennt, sondern sie als Teil der Wolke sieht. Das Aerosol verringert aber die Albedo der Wolke.
Somit wird auch das abgeleitete Wolkenprodukt eine zu geringe optische Dicke aufweisen. Da dieser Effekt zu erwarten war, wurden die Berechnung für die optischen Dicke
zusätlichen mit CloudSat-Messdaten und der Formel (3.5) für plan-parallele Wolken
durchgeführt.
5.4
Simulationsergebnisse und Auswertung
Die folgende Abbildung zeigt die Einzelstreualbedo in Abhängigkeit der Wellenlänge.
Wäre der Wert der Einzelstreualbedo gleich eins, würde es sich bei dem betrachteten
Teilchen um ein rein reflektierendes Teilchen handeln. Je kleiner der Wert der Ein-
5.4. SIMULATIONSERGEBNISSE UND AUSWERTUNG
41
zelstreualbedo wird, desto größer ist die absorbierende Eigenschaft des Teilchens. Die
Delle in der Einzelsteualbedo bei 3000 nm ist auf eine Wasserdampfabsorptionbande
und dem Einfluss der Aerosole zurückzuführen. Das sie so breit ausfällt liegt an der hier
relativ großen Intervallbreite, mit denen der Strahlungstransport in MOMO gerechnet
wird.
Abb. 5.6 Dargestellt ist die Einzelstreualbedo des urbanen Aerosols aus OPAC in Abhängigkeit
der Wellenlänge.
Abb. 5.7 Die Grafik zeigt den normierten Strahlungsfluss am Atmosphärenoberrand bei
verschiedenen optischen Dicken des Aerosols für die vier verschiedenen optischen Dicken der Wolke
(dargestellt durch die farbigen Linien). Dies gilt für einen Zenitwinkel der Sonne von 30°, was dem
Sonnenstand vom 13. August 2006 zum Zeitpunkt der Fallstudie entspricht.
42
KAPITEL 5. ERGEBNISSE
Der Einfluss einer Aerosolschicht über dem Wasser lässt sich einfach auswerten.
Man berechnet zum Einen den Fall einer Aerosolschicht mit einer optischen Dicke von
1.1 in einer sonst klaren Atmosphäre. Für diese Berechnung nimmt man eine Solarkonstante von 1367 W/m2 an. Für den Strahlungsfluss am Oberrand der Atmosphäre
erhält man einen Wert von 68 W/m2 , der Untergreund ist nur der Ozean mit einer
Albedo von 0,02 (ohne Wolke und Aerosol). Fügt man nun eine Aerosolschicht ein, so
führt dies zu einer Erhöhung desaufwärstgerichteten Strahlungsflusses auf 105 W/m2 ,
also einen um 37 W/m2 erhöhten Wert. Ist eine Wolke unterhalb der Aerosolschicht
vorhanden, ist zwar der Strahlungsfluss am Oberrand der Atmosphäre vergrößert, aber
auch der Anteil der in der Aerosolschicht absorbierte Energie vergößert sich. Dies ist
bei hohen optischen Dicken für die Wolke stark ausgeprägt, kann aber auch schon bei
einer geringen optischen Dicke von 3 beobachtet werden. Für eine wolkenoptische Dicke
von 10 erhält man statt eines Strahlungsflusses von 402 W/m2 einen um 107 W/m2
kleineren Wert, also 295 W/m2 . Ein solches Verhalten der Veränderung in den Strahlungswerten ist auf die absorbierende Eigenschaft der Aerosole zurück zuführen.
optische Dicke
Intensität ohne
Intensität mit Aerosol der
der Wolke
Aerosol in W/m
0
68
105
+ 37
3
215
183
- 32
10
402
295
- 107
30
661
401
- 260
2
optischen Dicke 1.1 in W/m
Strahlungsintensitäts2
differenz in W/m2
Tabelle 5.1 Strahlungsintensitäten bei einem Zenitwinkel von 30°, entsprechend des Sonnenstandes für Zeitpunkt und Ort der Fallstudie 2.
Die Veränderungen in der Strahlungsintensität lassen sich aber auch für kleinere
oder größere optische Dicken des Aerosols oder die unterschiedlichen Sonnenzenitwinkel berechnen. Die Grafiken für den Stahlungsfluss in Abhängigkeit der Zenitwinkel
sind im Anhang (7.1) zu finden. Aus diesen Grafiken wird deutlich, dass die Gesamtintensität bei größerem Zenitwinkel abnimmt. Die größte Intensität und damit auch der
größte Einfluss der Aerosole besteht beim Sonnenzenitwinkel 0°. Dies kommt allerdings
nur in den Tropen und in den entsprechenden Jahreszeiten vor. Eine Aerosolschicht
oberhalb einer Wolke bei diesem Sonnenwinkel zu finden, wird selten vorkommen. Andere Sonnenwinkel, zwischen 20° und 60°, sind auch in höheren Breiten häufig anzutreffen. Somit ist die Chance eine Situation, die dieser Fallstudie ähnlich ist, zu finden groß.
5.4. SIMULATIONSERGEBNISSE UND AUSWERTUNG
43
In absoluten Zahlen ist der Aerosoleffekt um so stärker, je optisch dicker die darunter liegende Wolke ist. Das heißt, dass die Aerosolschicht an Energie gewinnt und
sich die Atmosphäre in der Höhe der Aerosolschicht erhitzt. Die in der Aerosolschicht
absorbierte Strahlung lässt sich in eine Erwärmung in Kelvin [K] pro Tag umrechnen.
Um dies für unseren Fall 2 durchzuführen, braucht man den Zenitwinkel des Sonnenstandes für Ort und Tag der Fallstudie, die lokalen Werte für Temperatur, Druck und
relative Feuchte der Aerosolschicht sowie deren geometrische Dicke. Die von MOMO
berechneten Werte der Strahlungsintensität müssen dann nur noch mit folgender Formel in die Temperaturdifferenz pro Zeit umgerechnet werden:
I
∆T
=
cp ρ∆z
t
(5.1)
Die Dichte der Luftschicht berechnet sich folgendermaßen:
ρ=
p
Rf T
(5.2)
Für die Berechnung der Gaskonstante feuchter Luft Rf werden die Gaskonstanten
der trockenen Luft und die von Wasserdampf benötigt.Weiterhin muss man die Werte
für die relative Feuchte, die Temperatur und den Druck der Umgebungsluft kennen.
Diese findet man in den GFS-Daten für den 13. August 2006. Die Formel für die
Gaskonstante lautet wie folgt:
Rf =
Wobei gilt :
R1
1 − (φ ∗ ppd )(1 −
pd = 611.2P a ∗ e[
pd : Sättigungsdruck von Wasser in Luft
R1 : Gaskonstante der trockenen Luft
[J/kgK]
(5.3)
17.5 ∗ ν
]
214.2C + ν
• φ: relative Feuchte (80 %)
[hP a])
R1
)
Rd
• p: Druck der Umgebungsluft (725 hP a)
ν: Temperatur der Umgebungsluft [C]
Rd : Gaskonstante von Wasserdampf
[J/kgK]
44
KAPITEL 5. ERGEBNISSE
• I: Intensität der Strahlung [W/m2 ]
cp : Wärmekapazität von Luft (1005
J/kgK)
∆z: geometrische Höhe der
Aerosolschicht (2040 m)
∆T : Temperaturänderung [K]
• ρ : Dichte der Luft [kg/m3 ]
T : Temperatur [K]
Rf : Gaskonstante für feuchte Luft
(288,4 J/kgK)
t : Zeit [s]
Die Werte für den aufwärtsgerichteten Strahlungsfluss aus MOMO werden für 17
verschiedene Zenitwinkel ausgegeben. Ist der genaue Verlauf der Sonne bekannt, können die Strahlungsintensitäten als Tagesgang aufgetragen werden. Die Werte für die
einzelnen Winkel müssen dem Verlauf der Sonne entsprechend interpoliert werden. Am
13. August 2006 ist die Sonne im Golf von Guinea um 6:04 UTC aufgegangen. Der
Sonnenhöchststand wurde um 11:58 UTC erreicht und gegen 17:40 UTC wanderte die
Sonne hinter dem Horizont. Der Sonnenstand wurde mit dem Solar Position Calculator von Chris Cornwall, Aaron Horiuchi and Chris Lehman berechnet. Dieses Program
ist auf der Internetseite der NOAA zu finden. Dies kann für jeden Zeitpunkt und Ort
durchgeführt werden. Im Folgenden werden zwei Abbildungen für die Strahlungsintensität als Tagesgang gezeigt. Diese beiden Grafiken zeigen die Veränderungen in der
Strahlungsintensität für den Fall einer optischen Dicke von 10. Die Grafiken für die anderen wolkenoptischen Dicken sind im Anhand (7.2) zu finden. Wie zu erwarten war,
ist die Intensität zu Beginn und zum Ende eines Tages viel geringer als um die Mittagszeit. Der Einfluss der Aerosole ist deutlich erkennbar. Für die Fälle mit Wolken haben
die Aerosole eine abschwächende Wirkung, für den Fall ohne Wolke verstärkt sich die
Strahlungsintensität am Oberrand der Atmosphäre. Auffällig ist, dass die Strahlungsintensität bei geringer optischer Dicke der Wolke (3) oder ohne Wolke und hoher optische
Dicke des Aerosols in den Mittagsstunden nicht am höchsten ist. Dieses Artefakt tritt
nur für optisch dünne Fälle auf, wie in den Abbildungen 7.1 a,b und 7.3 a,b sichtbar
wird. Es ist durch die nicht exakte Modellierung des Ozeans und dessen Streuverhalten
zu begründen. In der Realität entspricht die Verteilung der Strahlungsintensität über
den Tag einem Verlauf wie er in Abbildung 5.8 gezeigt wird. Die Intensität ist um
den Mittag also bei Sonnenhöchststand am größten und geht zum Sonnenaufgang bzw.
Sonnenuntergang gegen Null. In der Nacht hat man keine solare Einstrahlung.
5.4. SIMULATIONSERGEBNISSE UND AUSWERTUNG
45
Abb. 5.8 Die Grafik zeigt den solaren Strahlungsfluss in W/m² als Tagesgang. Der Verlauf spiegelt
den Sonnenverlauf des 13. Augusts 2006 im Golf von Guinea wieder. Die schwarze Linie kennzeichnet
den Fall ohne Aerosolschicht. Die farbigen Linien beschreiben den Strahlungsverlauf für die
unterschiedlichen optischen Dicken der Aerosolschicht (von oben nach unten zunehmende
aerosoloptische Dicke). Die optische Dicke der Wolke ist 10.
Abb. 5.9 Der Sonnenzenitwinkel ist gegen die Tageszeit aufgetragen und beschreibt somit die
Wanderung der Sonne entlang des Himmels für den 13. August 2006.
46
KAPITEL 5. ERGEBNISSE
Als nächstes wird die Grafik für die Temperaturerhöhung pro Tag gezeigt. Die
Berechnung erfolgt über die oben genannte Formel (5.1). Aufgetragen ist die Temperaturdifferenz zwischen dem jeweiligen Fall für die Wolke mit einem Aerosol und dem
ohne Aerosol. Zur genauen Auswertung ist dies noch mal in Tabellenform (Tabelle 5.2)
aufgeführt. Abzulesen sind Temperaturerhöhungen von bis zu 5 K pro Tag. Für eine
optisch sehr dicke Wolke (30) und ein ebenfalls optisch dickes Aerosol (1.5) entspricht
dies einer Heizrate von gemittelt ca. 0.5 K pro Stunde, wobei in den Morgen- und
Abendstunden relativ wenig im vergleich zu den Mittagsstunden passiert. Die negativen Werte für die Kurve des wolkenlosen Falls ist allerdings nicht als Abkühlung der
Aerosolschicht aufzufassen, sondern eher als Energie, die ohne Aerosol dem Ozean zugeführt werden würde. Wenn sich eine Aerosolschicht über einem sehr dunklen (nahezu
schwarzen) Untergrund wie dem Ozean befindet, kommt der reflektierende Anteil sehr
viel stärker zum Tragen als wenn sich unterhalb des Aerosols eine helle (fast weiße)
Wolkenschicht befindet.
Abb. 5.10 Aufgetragen ist die Temperaturdifferenz in der Aerosolschicht von 2040 m gegen die
optische Dicke des Aerosols. Die farbigen Linien markieren je eine optische Dicke der Wolke. Die
Differenz bezieht sich auf den jeweiligen Fall minuns dem Fall ohne Aerosolschicht.
5.4. SIMULATIONSERGEBNISSE UND AUSWERTUNG
47
optische Dicke T in K T in K T in K T in K
des Aerosols
opt 0
opt 3
opt 10
opt 30
0
0
0
0
0
0.5
-0.54
0.51
1.56
2.51
0.7
-0.68
0.64
2.00
3.24
0.8
-0.74
0.70
2.19
3.56
0.9
-0.8
0.75
2.37
3.86
1.0
-0.82
0.80
2.54
4.14
1.1
-0.90
0.85
2.83
4.39
1.2
-0.94
0.89
2.83
4.62
1.3
-0.98
0.92
2.96
4.84
1.5
-1.05
0.99
3.19
5.23
Tabelle 5.2 In der Tabelle sind die theoretischen Temperaturerhöhungen für einen Tag
eingetragen. Dies gilt für die Berechnungen für den Sonnenverlauf am 13. August 2006 (8°S,
1.6°O). Die betrachtete Schicht hat eine Mächtigkeit von 2040m.
Die Veränderungen in den Erwärmungen bei einem um nur 10% veränderten Absorptionskoeffizienten können bei optisch dicken Aerosolschichten bis zu 0.3 K betragen.
Die Änderungen in der Strahlungintensität und der damit verbundenen Erwärmung in
der Aerosolschicht sind also auch abhängig von dem spektralen Verhalten der Einzelstreualbedo. Die Einzelstreualbedo gibt Rückschlüsse auf die Absorptionsfähigkeit der
Aerosole und zeigt auch Reaktionen auf kleine Veränderungen. hin stark empfindlich.
Die Auswirkungen sind zwar nicht mit denen der Veränderung der optischen Dicke zu
vergleichen, aber sie sind nicht zu vernachlässigen um genaue Abschätzungen durchführen zu können.
Die in Abb. 5.8 gezeigten Erwärmungsraten sind ohne Abstrahlung berechnet worden. Real wird die Temperatur der Aerosolschicht also nicht um bis zu 5 K steigen.
Durch die Erwärmung erhöht sich zwar die Temperatur, allerdings hat dies eine Erhöhung der Abstrahlung zur Folge was die Temperatur wieder mindert. Trotzdem wird
netto eine Temperaturerhöhung in der Aerosolschicht stattfinden. Dies wird sicherlich
eine Verstärkung der vorhandenen Inversion oder die Bildung einer zweiten Inversionsschicht auslösen. Auch kann die erwärmte Luft die Schichten oberhalb der Aerosole
labilisieren. Ob dies ausreicht um eine neue Wolkenschicht entstehen zu lassen, ist nicht
Fragestellung dieser Arbeit. Es ist aber damit zu rechnen, dass eine erwärmte Aerosolschicht dynamische Effekte auslöst. Um gute Abschätzungen dieser Effekte zu erhalten,
48
KAPITEL 5. ERGEBNISSE
b
a
Abb. 5.11 Die Abbildungen a und b zeigen die Temperaturdifferenz zwischen den berechneten
Heizraten mit verändertem Absorptionskoeffizienten (für a um 5%, für b um 10% reduziert) und den
bereits gezeigten Heizraten.
müssen sehr viel genauere und großflächigere Messungen von Fällen ähnlich der Fallstudie durchgeführt werden.
Führt man die selben Untersuchungen, wie die der Fallstudie, über Landflächen
statt über dem Ozean durch, werden sich andere Auswirkungen ergeben. Im Fall einer optisch sehr dicken Wolke ist nur mit kleinen Änderungen zu rechen. Bei dünnen
Wolken oder ohne Wolkenschicht unterhalb der Aerosolschicht kommt es sehr auf die
Bodenalbedo an. Um hierfür eine genaue Abschätzung zu erhalten, müssten neue Strahlungstransportrechnungen durchgeführt werden.
Kapitel 6
Zusammenfassung
Die Aufgabe dieser Arbeit war es, den direkten Einfluss von biomass burning aerosols über Wolken zu bestimmen. Die Berechnungen dafür habe ich im Rahmen einer
Sensitivitätsstudie durchgeführt. Innerhalb dieser Sensitivitätsstudie ist die Fallstudie,
die am 13. August 2006 im Golf von Guinea stattfand, wiederzufinden. Die Ergebnisse der Sensitivitätsstudie wurden mit Messdaten anderer Satelliten und Daten aus
dem GFS Vorhersagemodell sowie den Berechnungen der Rückwärtstrajektorien der
Aerosole ergänzt, um der Sensitivitätsstudie und der Fallstudie einen möglichst reellen
Rahmen zu bieten.
Als erstes Ergebnis ist festzuhalten, das die optische Dicke der Wolken einen extremen Einfluss auf die Strahlungsbilanz vorweist. Der errechnete Trend bei zusätzlicher
Aerosolschicht oberhalb der Wolken ist in zwei Gruppen einzuteilen. Einmal verstärkt
das Aerosol die Strahlungsintensität. In der Fallstudie würde sich die Strahlungsintensität am Oberrand der Atmosphäre um 37 W/m2 erhöhen, wenn sich keine Wolke
sondern ausschließlich der dunkle Ozean unterhalb des Aerosols befände. In der Strahlungsbilanz ist nur der reflektierende Anteil des Aerosols zu sehen. Zweitens kann das
Aerosol die Strahlungsintensität verringern. Diese ist weitaus größer als die bereits erwähnte Strahlungsverstärkende Wirkung. Sie verstärkt sich mit zunehmender optischer
Dicke der Wolken- und Aerosolschicht. Hier setzt sich also die absorbierende Eigenschaft
durch. In der Strahlungsbilanz am Oberrand der Atmosphäre ist eine Strahlungsminderung zu verzeichnen, was auf die absorbierende Wirkung hinweist. Über dem schwarzen
Ozean ist das Aerosol vergleichsweise hell und wirkt deshalb reflektierend. Über einer
weißen Wolke ist es jedoch dunkel und stark absorbierend.
Die Sensitivitätsstudie hat somit gezeigt, das biomass burning aerosols oberhalb
von Wolken einen nicht zu vernachlässigenden Einfluss auf den Strahlungshaushalt ha49
50
KAPITEL 6. ZUSAMMENFASSUNG
ben. Für optisch dicke Wolken in Kombination mit optisch dicken Aerosolen können
Minderungen in der Strahlungsintensität am Oberrand der Atmosphäre von bis zu 260
W/m2 erreicht werden. Auf einen Tag gesehen kann dies zu einer Temperaturerhöhung
von über 5 K führen. Aber auch für optisch dünne Wolken ist der Einfluss einer Aerosolschicht oberhalb der Wolke deutlich erkennbar. Die bei dieser Kombination von
Wolken und Aerosolen entstehende Minderung der Strahlungsintensität sollte nicht außer Acht gelassen werden.
Der direkte Einfluss von Aerosolen oberhalb von Wolken und der somit entstehenden Temperaturerhöhung kann beispielsweise eine Auflösung der Wolken unterhalb
der Aerosolschicht zur Folge haben. Auch kann die erhöhte Temperatur in der Aerosolschicht eine dynamische Bewegung auslösen oder eine verstärkte Abstrahlung innerhalb
der Aerosolschicht bewirken. Diese Effekte können als Fragestellung anderer Arbeiten
dienen.
Diese Arbeit zeigt, dass die Veränderungen in der Strahlunsgsbilanz in den Klimamodellierungnen berücksichtigt werden sollten. Solange aber keine genauen Kenntnisse
über die Häufigkeit der Wolken und Aerosolkombinationen vorliegt, wird es schwer
sein eine Parametrisierung dafür zu erstellen. Auch ist eine bessere Erforschung der
Aerosole und deren spektralen Eigenschaften für eine solche Aufgabe nötig. Auch wenn
noch viele Fragen offen bleiben, konnte mit dieser Arbeit zeiget werden, dass der direkte Einfluss von stark absorbierenden Aerosolen, wie dem biomass burning aerosols,
in Kombination mit einer Wolkenschicht unterhalb der Aerosolschicht eine strahlungsmindernde Wirkung hat.
Kapitel 7
Anhang
51
52
KAPITEL 7. ANHANG
7.1
Normierter Strahlungsfluss
a
b
Abb. 7.1 Gezeigt wird der normierte Strahlungsflussg aufgetragen gegen die verschiedenen
Zenitwinkel. Die optische Dicke der Wolke ist für Abb. a 0 und für Abb. b 3. Die optische Dicke der
Aerosolschicht nimmt für Abb. a von unten nach oben, für Abb. b von oben nach unten zu.
7.1. NORMIERTER STRAHLUNGSFLUSS
53
a
b
Abb. 7.2 Gezeigt wird der normierte Strahlungsflussg aufgetragen gegen die verschiedenen
Zenitwinkel. Die optische Dicke der Wolke ist für Abb. a 10 und für Abb. b 30. Die optische Dicke
der Aerosolschicht nimmt für beide Abbn. von oben nach unten zu.
54
KAPITEL 7. ANHANG
7.2
Tagesgang des Strahlungsflusses in W/m²
a
b
Abb. 7.3 Die Grafiken zeigen den solaren Strahlungsfluss in W/m² als Tagesgang. Der Verlauf
spiegelt den Sonnenverlauf des 13. Augusts im Golf von Guinea wieder. Die optische Dicke der
Aerosolschicht nimmt für Abb. a von unten nach oben, für Abb. b von oben nach unten zu. In Abb.
a ist keine Wolke unterhalb der Aerosolschicht. Die optische Dicke der Wolke in Abb. b beträgt 3.
7.2. TAGESGANG DES STRAHLUNGSFLUSSES IN W/M²
55
a
b
Abb. 7.4 Die Grafiken zeigen den solaren Strahlungsfluss in W/m² als Tagesgang. Der Verlauf
spiegelt den Sonnenverlauf des 13. Augusts im Golf von Guinea wieder. Die optische Dicke der
Aerosolschicht nimmt von oben nach unten zu. In Abb. a ist die optische Dicke der Wolke 10, in
Abb. b ist eine Wolke der optischen Dicke 30 vorhanden.
56
7.3
KAPITEL 7. ANHANG
Heizraten pro Tag
b
a
c
Abb. 7.5 In diesen Abbildungen werden die Heizraten pro Tag dargestellt als Erwärmung in K. Die
farbigen Linien markieren die unterschiedlichen optischen Dicken der Wolke. Die optischen Dicke der
Aerosolschicht ist an der x-Achse ablesbar. Abb. a ist für die unveränderte Einzelstreualbedo, in
Abb. b und c sind die Einzelstreualbeden (Absorptionskoeffizient um 5% bzw. um 10%) verringert.
7.3. HEIZRATEN PRO TAG
a
57
b
Abb. 7.6 Hier ist die Differenz zwischen den Erwärmungsraten für die unveränderte und die
verringerten Einzelstreualbeden dargestellt. Abb. a zeigt die Differenz zwischen Abb. 7.5a und 7.5b,
Abb. b zeigt die Differenz zwischen Abb. 7.5a und 7.5c.
58
KAPITEL 7. ANHANG
Kapitel 8
Danksagung
Als erstes möchte ich mich bei Prof. Dr. J. Fischer bedanken, der mir diese Arbeit
ermöglicht hat. Die Arbeit am Institut für Weltraumwissenschaften hat mein Interesse
für die Fernerkundung noch verstärkt. Ein großer Dank geht auch an Dr. R. Preusker.
Die Atmosphäre in der Arbeitsgruppe und die tolle kollegiale Zusammenarbeit haben
mir sehr geholfen und gefallen. Hier bedanke ich mich bosonders bei Rasmus Lindstrot,
der mir meine vielen Fragen beantwortete und mir immer neue Sichtweisen auf die Probleme gegeben hat. Ein weiterer Dank geht an Dr. Anja Hühnerbein, die mir MOMO
erklärt hat.
Weiterhin möchte ich meiner ganzen Familie danken. Meine Eltern haben mit ihrer
moralischen und finanziellen Unterstütung einen großen Beitrag zur Ermöglichung der
Arbeit geleistet. Auch möchte ich Michael Faber danken, der für fachliche Diskusionen
und moralische Unterstützung jederzeit für mich da war.
59
60
KAPITEL 8. DANKSAGUNG
Kapitel 9
Abkürzungen und Quellen der
Abbildungen
9.1
Abkürzungen
• CALIPSO :
• CALIPO :
Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation
Cloud-Aerosol LIdar with Orthogonal Polarisation
• CNES :
• CNRM :
Centre National d’Etudes Spatiales
Centre National de Recherches Meteorologiques
• CPR :
Cloud Profiling Radar
• EOS :
Earth Observing System
• GDAS :
Global Data Assimilation System
• GFS :
Global Forecast System
• GMEI :
Groupe de Meteorologie Experimentale et Instrumentale
• IPCC :
Intergovernmental Panel on Climate Change
• MSG :
Meteosat Second Generation
• MODIS :
Moderate Resolution Imaging Spectrometer
• NASA :
National Aeronautics and Space Administration
• NOAA :
National Oceanic and Atmospheric Administration
• OCO :
Orbiting Carbon Observatory
61
62
KAPITEL 9. ABKÜRZUNGEN UND QUELLEN DER ABBILDUNGEN
• OPAC :
• PARASOL :
Optical Properties of Aerosols and Clouds
Polarisation & Anisotropy of Reflectances for Atmospheric Sciences
coupled with Observations from a Lidar
• SAFARI :
Southern African Regional Science Initative
• SEVERI :
Spinning Enhanced Visible and Infrared Pathfinder
• WMO :
World Meteorological Organization
• WWF :
World Wide Fund For Nature
9.2
Quellen der Abbildungen
• Quelle der Abbn. 1.1, 1.2
• Quelle der Abbn. 1.3, 5.11
• Quelle der Abb. 2.1
• Quelle der Abbn. 2.2, 3.5
• Quelle der Abb. 2.3
NASA / Reuters
NASA, www.nasa.gov
Global Warming Art, www.globalwarmingart.com
Bernhard Mühr, Karlsruher Wolkenatlas
IPCC Report 2001
• Quelle der Abbn. 2.4, 2.5
Sobolev, A Treatise on Radiativ Transfer
• Quelle der Abbn. 3.1-3.3
NASA, www.nasa.gov
• Quelle der Abb. 4.4
• Quelle der Abb. 5.10
Rasmus Lindstrod
NOAA, www.noaa.gov
Kapitel 10
Literaturverzeichnis
1. Bennartz, R., Global assessment of marine boundary layer cloud droplet number concentration from satellite, J. Geophy. Res., 112, D02201, 2007
2. Cooperative Institute for Research in the Atmosphere, CloudSat Standart Data Products
Handbook, 2006
3. Hünerbein, A., Fernerkundung des solaren aufwärstgerichteten Strahlungsflusses über
Wolken mit räumlich hochaufgelösten Satellitenmessungen, Dissertation am Institut für
Weltraumwissenschaften, FU-Berlin, 2006
4. Eck,T. F.,B. N. Holben, D. E. Ward, M. M. Mukelabai, O. Dubovik, A. Smirnov, J.
S. Schafer, N. C. Hsu, S. J. Piketh, A. Queface, J. Le Roux, R. J. Swap, I. Slutsker,
Variabilaty of biomass burning aerosol optical characteristics in southern Africa durig
the SAFARI 2000 dry season campaign and a comparison of single scattering albedo
estimates from radiometric measurements, J. Geophy. Res., 108, SAF 13, 2003
5. Ficher, Prof. Dr. J., P. Albert, J. Odebrecht, Vorlesungsskript Strahlung, Institut für
Wletraumwissenschaften, 2002
6. Fell, F., Validierung eines Modells zur Simulation des Strahlungstransportes in Atmosphäre und Ozean, Dissertation am Institut für Weltraumwissenschaften, FU-Berlin,
1997
7. Fell, F., J. Fischer, Numerical simulations of the light field in the atmosphere-ocean
system using the matrix-operator method, J. Quantitative Spectroscopy and Radiative
Transfer, Vol. 69, 351-388, 2001
8. Forster, P., V. Ramaswamy, P. Artaxo, T. Berntsen, R. Betts, D. W. Fahey, J. Heywood, J. Lean, D. C. Lowe, G. Myhre, J. Nganga, R. Prinn, G. Raga, M. Schulz and R.
Van Dorland, Changes in Atmospheric Constituents and in Radiativ Forcing, The Physical Basis. Contribution of Working Group I to the Fourth Assessment Report of the
63
64
KAPITEL 10. LITERATURVERZEICHNIS
Intergovernmental Panel on Climate Changes, Cambridge University Press, Cambridge,
United Kingdon and New York, NY, USA, 2007
9. Goody, R. M. and Y. L. Yung, Atmospheric Radiation Theoretical Basis, Oxford University Press, 1989
10. Hess, M., P. Koepke, I. Schult, Optical Properties of Aerosols and Clouds, B. A. Met.
Society, Vol. 79, 831-844, 1998
11. Hopkins, R. J., K. Lewis, Y. Desyaterik, Z. Wang, A. V. Tivanski, W. P. Arnott, A.
Laskin, M. K. Gilles, Correlations between optical, chemical and physical properties of
biomass burning aerosols, Geophy. Res. Let., 34, L18806, 2007
12. Kiehl,J. T., V. Ramanathan, Comparison fo Cloud Forcing Derived From the Earth Radiation Budget Experiment With That Simmulated by the NCAR Community Climate
Model, J. Geophy. Res., 95, 11 679-11 698, 1990
13. King, M. D., J. Closs, S. Spangler, R. Greenstone, EOS Data Handbook, 2003
14. Kondratyev, Y., Radiation in the Atmosphere Academic Pr, 1999
15. Labonne, M., F.-M. Bréno, F. Chevallier, Injection height of biomass burning aerosols
as seen from a spaceborne lidar, Geophy. Res. Let., L11806, 2007
16. Liljequist, G. H., K. Cehak, Allgemeine Meteorologie,Springer, 1984
17. Petty, G. W., A First Course in Atmospheric Radiation, Sundog Publishing 2004
18. Product Description Document: NCEP Model Analyses & Forecasts, 2008
19. Ramanathan, V., Bruce R. Barkstrom, Edwin F. Harrison, Climate and the Earth’s
Radiatuin Budget, Int. Agrophysics, 5, 171-181, 1989
20. Schüller, L., Fernerkundung von klimarelevanten Wolkenparametern mit satelliten- und
flugzeuggestützten Radiometern, Dissertation am Institut für Weltraumwissenschaften,
FU-Berlin,2000
21. Sobolev, V. V., A Treatise on Radiativ Transfer, D. Van Nortrand Company, 1963
22. Spring,S., HYSPLIT Modell Research, www.noaa.gov, 2008
23. Swap,R. J., H. J. Annegarn, J. T. Suttles, M. D. King, S. Platinck, J. L. Privette, R. J.
Scholes, Africa burning: A thematic analysis of the Southern African Regional Science
Initiative (SAFARI 2000), J. Geophy. Res., 108, SAF 1, 2003
24. Tilmes, S., R. Müller and R. Salawitch, The sensitivity of polar ozone depletion to
proposed geo-engineering schemes, Science Express, 2008
65
25. Winkler, D. M., C. A. Hosteltler, M. A. Vaughan, A. H. Omar,CALIOP Algorithm
Theoretical Basis Document, 2006
26. WWF, Hintergrundinformation Waldbrände
66
KAPITEL 10. LITERATURVERZEICHNIS
Eigenständigleitserklärung
Ich versichere hiermit, daß ich die vorstehende Arbeit selbstständig verfaßt und keine
anderen als die angegebenen Hilfsmittel benutzt habe. Die Stellen, die anderen Werken
dem Wortlaut oder dem Sinn nach entnommen wurden, habe ich in jedem einzelnen Fall
durch die Angabe der Quelle, auch der benutzten Sekundärliteratur, als Entlehnung
kenntlich gemacht.
Datum
Antonia Haser