Anwengungen geometrischer Abbildungen Kongruenz

Anwengungen geometrischer Abbildungen
Kongruenz- und Ähnlichkeitsabbildung
Amina Duganhodzic
Proseminar: Mathematisches Problemlösen
Unter der Leitung von Privat Dozentin Dr. Natalia Grinberg
26. Juni 2015
Karlsruher Institut für Technologie
Fachbereich Mathematik
Inhaltsverzeichnis
1 Kongruenz- und Ähnlichkeitsabbildungen
1.1
2
Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.1.1
Kongruenzabbildung . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.1.2
Ähnlichkeitsabbildung . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.2
Beispiel 1: Rotkäppchen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.3
Beispiel 2: Bühnenscheinwerfer . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.4
Beispiel 3: Punkte auf einem Dreieck . . . . . . . . . . . . . . . . . . . . .
5
1.5
Beispiel 4: Torte und Schokolade . . . . . . . . . . . . . . . . . . . . . . . .
6
2 Klassifizierung der Kongruenzabbildungen und deren Verkettung
2.1
7
Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.1.1
Positive und negative Orientierung . . . . . . . . . . . . . . . . . .
7
2.1.2
Gleich- und Gegensinnigkeit . . . . . . . . . . . . . . . . . . . . . .
7
2.2
Beispiel 5: Ähnlichkeitsabbildung . . . . . . . . . . . . . . . . . . . . . . .
8
2.3
Beispiel 6: Kongruenzabbildung mit zwei Fixpunkten . . . . . . . . . . . .
9
2.4
Beispiel 7: Kongruenzabbildung mit einem Fixpunkt . . . . . . . . . . . . .
9
2.5
Beispiel 8: Translation oder Gleitspiegelung
2.6
Beispiel 9: Geraden mit Schnittpunkt . . . . . . . . . . . . . . . . . . . . . 13
2.7
Beispiel 10: Satz von Napoleon
2.8
Beispiel 11: Kollineare Mittelpunkte . . . . . . . . . . . . . . . . . . . . . . 15
. . . . . . . . . . . . . . . . . 10
. . . . . . . . . . . . . . . . . . . . . . . . 14
3 Schließungssätze
16
3.1
Beispiel 12: Ente schwimmt im Teich . . . . . . . . . . . . . . . . . . . . . 16
3.2
Beispiel 13: Thomsenstreckenzug . . . . . . . . . . . . . . . . . . . . . . . 17
4 Literaturverzeichnis
18
1
Kapitel 1
Kongruenz- und
Ähnlichkeitsabbildungen
1.1
Definitionen
1.1.1
Kongruenzabbildung
Eine bijektive Abbildung T : R2 → R2 heißt Kongruenzabbildung, wenn für je
zwei Punkte A und B gilt:
|A0 B 0 | = |AB| mit A0 = T (A) und B 0 = T (B)
1.1.2
[1]
Ähnlichkeitsabbildung
Eine bijektive Abbildung T : R2 → R2 heißt Ähnlichkeitsabbildung, wenn es
ein λ > 0 gibt mit der Eigenschaften, dass für je zwei Punkte A und B gilt:
|A0 B 0 | = λ|AB| mit A0 = T (A) und B 0 = T (B)
[1]
Aus der Definition der Ähnlichkeitsabbildung wird ersichtlich, dass es sich bei jeder Ähnlichkeitsabbildung mit λ = 1 um eine Kongruenzabbildung handelt. Dadurch ergeben sich
die folgenden Folgerungen:
1. Wenn T eine Kongruenz- bzw. Ähnlichkeitsabbildung ist, so ist die zu T inverse
Abbildung T −1 ebenfalls eine Kongruenz- bzw. Ähnlichkeitsabbildung.
2. Wenn T1 und T2 Kongruenz- bzw. Ähnlichkeitsabbildung sind, so ist auch deren Verkettung (auch Hintereinanderausführung oder Komposition genannt) T2 ◦T1 ebenfalls
eine Kongruenz- bzw. Ähnlichkeitsabbildung.
2
1.2
Beispiel 1: Rotkäppchen
Aufgabenstellung
Rotkäppchen wohnt in Punkt A und ihre Oma in Punkt B. Sie soll zum Fluss laufen,
dort Wasser schöpfen und dieses zu ihrer Oma bringen. Der Gesamtlaufweg soll minimal
sein.
Wie muss Rotkäppchen laufen?
Lösung
Das Flussufer sei durch eine Gerade g gegeben. Weiter wird der Punkt B an der Geraden g
gespiegelt, wodurch der Punkt B 0 erzeugt wird. Sei Y ∈ g, der Punkt zu dem Rotkäppchen
hinläuft, und die Gesamtstrecke l, die sie zurücklegen muss, gegeben. So gilt für l:
l = |AY | + |Y B| = |AY | + |Y B 0 |
|AY | + |Y B 0 | ist genau dann minimal, wenn die Punkte A, Y und B 0 eine Gerade bilden.
Somit sollte Rotkäppchen zum Schnittpunkt X = (AB 0 ) ∩ g laufen.
Abbildung 1.1: Rotkäppchens Weg (der gestrichelte Weg ist der kürzeste)
3
1.3
Beispiel 2: Bühnenscheinwerfer
Aufgabenstellung
Ein Bühnenscheinwerfer strahlt senkrecht auf den Boden.
a) Der Schatten eines Quaders soll maximal sein. Wie muss man ihn hierfür halten?
b) Der Schatten eines regelmäßigen Tetraeders mit Kantenlänge 1 soll maximal sein.
Wie groß ist dieser Schatten?
Lösung
a) Zuerst stellt sich die Frage, auf welche Ebene der Quader projiziert werden soll,
damit dessen Schatten maximal wird.
Die sichtbare Seite stellt drei Parallelogramme dar, dies gilt ebenfalls für den Schatten. Die Gesamtfläche ist somit die doppelte Fläche |ABC| des Dreiecks ABC.
Daraus folgt: Die Projektionsfläche wird dann maximal, wenn die Projektionsebene parallel zur Ebene des Dreiecks ABC ist, d.h. strahlt der Bühnenscheinwerfer
senkrecht nach unten, muss der Quader so gehalten werden, dass die Ebene ABC
horizontal ist.
Abbildung 1.2: Quader
Abbildung 1.3: Tetraeder
b) Hierbei stellt sich eine ähnliche Frage wie bei dem Quader, auf welche Ebene soll
der Tetraeder projiziert werden, damit dessen Fläche maximal wird.
Man bezeichne die Projektion des Vierecks mit ADBC. Des Weiteren benenne man
die Mittelpunkte der Strecken (AD), (DB), (BC) und (CA) mit X, Y, Z und W .
Mit Hilfe der Ähnlichkeit erhält man:
|DXY | = 41 |DAB|, |CW Z| = 14 |CAB|, |AXW | = 41 |ADC|, |BY Z| = 41 |BDC|
Hiermit erhält man, dass die Gesamtfläche des Tetraeders ADBC das Doppelte der
Fläche |XY ZW | des Parallelogramms XY ZW ist, da
4
|XY ZW | = |ABDC| − |DXY | − |CW Z| − |AXW | − |BY Z|
= |DBC| − 14 (|DAB| − |CAB|) − 14 (|ABC| − |BDC|)
= |ADBC| − 14 |ADBC| − 14 |ADBC| = 12 |ADBC|
Mit dem Satz der Mittelparallelen gilt weiter:
|XY | = |W Z| = 12 |AB| ≤
1
2
und ebenso |Y Z| = |XW | = 12 |DC| ≤
1
2
(Anmerkung: |AB| ≤ 1 und |DC| ≤ 1, da die Projektion einer Strecke nicht länger
als die Strecke selbst ist)
⇒ |ADBC| = 2|XY ZW | ≤ 2|XY | · |Y Z| · sin ∠(XY Z) ≤ 2 · 12 · 12 · 1 =
1
2
Gleichheit ist genau dann möglich, wenn die Projektionsebene parallel zu einem Paar
gegenüberliegender Kanten des Tetraeders bzw. parallel zum Quadrat XY ZW ist.
1.4
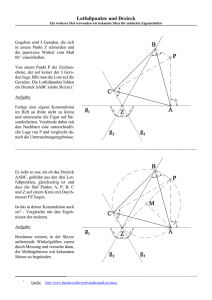
Beispiel 3: Punkte auf einem Dreieck
Aufgabenstellung
Gegeben seien ein spitzwinkliges Dreieck ABC und ein Punkt X, der auf der Strecke AB
liegt.
Zu finden ist ein Punkt Y ∈ (BC) und Z ∈ (CA), so dass lX = |XY | + |Y Z| + |ZX|
minimal ist.
Abbildung 1.4: lX soll minimiert werden
Lösung
Zu aller erst wird der Punkt X an (BC) und an (AC) gespiegelt, so dass man die Punkte
X 0 und X 00 erhält. Hierbei ist trivial, dass |XY | = |X 0 Y | und |XZ| = |X 00 Z|. Daraus
resultiert:
lX = |X 0 Y | + |Y Z| + |ZX 00 | ≥ |X 0 X 00 |
Daraus folgt, dass die Gesamtlänge genau dann minimal ist, wenn die Punkte X 0 , Y, Z
und X 00 kollinear sind.
Die Lösung lautet somit: Y = (X 0 X 00 ) ∩ (BC) und Z = (X 0 X 00 ) ∩ (AC)
5
1.5
Beispiel 4: Torte und Schokolade
Aufgabenstellung
Man nehme eine rechteckige Tafel Schokolade und lege sie auf eine ebenfalls rechteckige
Torte. Das Ziel ist die Torte und die Schokolade so mit einem geraden Messerschnitt zu
teilen, dass beide Rechtecke halbiert werden.
Wie muss man hierfür vorgehen?
Lösung
Aufgrund dessen, dass Rechtecke punktsymmetrisch sind, kann man sie durch einen
Schnitt durch ihr Zentrum in zwei kongruente Teile teilen. Daher ergibt sich die Strategie, dass man eine Gerade finden muss, die das Zentrum beider Rechtecke (Torte und
Schokolade) enthält. Liegen die Zentren übereinander, so kann man eine beliebige Gerade
wählen.
Abbildung 1.5: Torte und Schokolade (mit Zentren)
6
Kapitel 2
Klassifizierung der
Kongruenzabbildungen und deren
Verkettung
2.1
Definitionen
2.1.1
Positive und negative Orientierung
Ein Dreieck 4ABC – die Reihenfolge ist hierbei entscheidend – heißt positiv
orientiert, wenn beim Durchlaufen des Umkreises gegen den Uhrzeigersinn auf
die Ecke A zuerst die Ecke B und dann die Ecke C folgt. Folgt auf A dagegen
zuerst C und dann B, so heißt 4ABC negativ orientiert.[1]
2.1.2
Gleich- und Gegensinnigkeit
Eine Kongruenzabbildung heißt gleichsinnig, wenn das Bild jedes positiv orientierten Dreiecks positiv orientiert ist. Die Abbildung heißt gegensinnig, wenn
das Bild jedes positiv orientierten Dreiecks negativ orientiert ist.[1]
7
2.2
Beispiel 5: Ähnlichkeitsabbildung
Aufgabenstellung
Es sei T eine beliebige Ähnlichkeitsabbildung und mit 0 wird das Bild bei der Abbildung
T bezeichnet. Die Winkel sind hierbei nicht orientiert. Man beweise folgende Aussagen.
1) Wenn A, B und C drei nichtkollineare Punkte sind, dann gilt ∠ABC = ∠A0 B 0 C 0 .
2) Das Bild einer Geraden ist wiederum eine Gerade.
3) Sind zwei Geraden l1 und l2 parallel, so sind ihre Bilder T (l1 ) und T (l2 ) ebenfalls
zueinander parallel.
4) Das Bild eines Kreises mit Radius R ist wiederum ein Kreis, wobei der Radius λR
ist.
Beweis
1) Mithilfe der Anwendung der Definition der Ähnlichkeitsabbildung erhält man:
|B 0 C 0 | : |BC| = |C 0 A0 | : |CA| = |A0 B 0 | : |AB| = λ
⇒ Die entsprechenden Winkel sind gleich.
2) Für drei kollineare Punkte A, B und C gilt ohne Einschränkungen der Allgemeinheit
|AC| = |AB| + |BC| . Wendet man auch hier die Definition der Ähnlichkeitsabbildung an, erhält man wiederum |A0 C 0 | = |A0 B 0 | + |B 0 C 0 |.
⇒ Die Punkte A0 , B 0 und C 0 sind ebenfalls kollinear
3) Man nehme an, dass die Geraden T (l1 ) und T (l2 ) parallel sind und sich im Punkt
X schneiden. Aufgrund dessen dass die Gerade T bijektiv ist, besitzt der Punkt X
ein Urbild X0 mit X = T (X0 ) und da X der Schnittpunkt beider Geraden ist, liegt
dessen Urbild X0 auf den Geraden l1 und l2 .
⇒ Widerspruch: Die Geraden l1 und l2 haben keinen Schnittpunkt, da sie parallel
zueinander sind.
⇒ Die Bilder T (l1 ) und T (l2 ) müssen ebenfalls parallel sein.
4) Um einen Punkt O spanne man einen Kreis K = {X ∈ R2 : |OX| = R} mit Radius
R. Dann gilt aber auch K 0 = T (K) = {X 0 ∈ R2 : |O0 X 0 | = λR}, dies bildet hingegen
einen Kreis um den Punkt O0 = T (O) mit Radius λR ab.
8
2.3
Beispiel 6: Kongruenzabbildung mit zwei Fixpunkten
Aufgabenstellung
Gegeben sei eine Kongruenzabbildung T mit zwei verschiedenen Fixpunkten A und B,
wobei A 6= B, A0 = A und B 0 = B gelten.
Zu zeigen: T ist entweder die Spiegelung S(AB) an der Geraden (AB) oder die Identitätsabbildung id.
Beweis
Zu Beginn werden mithilfe der Abstände |AX| und |BX| alle Punkte X ∈ (AB) eindeutig
bestimmt. Schnell erhält man, dass X 0 = X, da
|AX| = |A0 X 0 | = |AX 0 |und|BX| = |B 0 X 0 | = |BX 0 |
(2.1)
Daraus folgt, dass jeder Punkt X auf der Geraden (AB) einen Fixpunkt der Abbildung
T repräsentiert. Aufgrund dessen werden folgende beide Fälle untersucht:
1. ∃ Fixpunkt C ∈
/ (AB)
2. @ weiteren Fixpunkte ∈
/ (AB)
Ad 1: T ist Identitätsabbildung. T kann durch die Bilder dreier nichtkollinearer Punkte
eindeutig bestimmt werden, es gilt also: id(A) = T (A), id(B) = T (B) und id(C) = T (C).
Identisch dazu ist somit id = T .
Ad 2: Hierbei wird ein beliebiger Punkt X ∈
/ (AB) betrachtet und sein Bild X 0 gefunden.
Da (2.1) gilt, existieren nur zwei Optionen für die Lage des Punktes X 0 : Zum einen ist
X = X 0 oder zum anderen ist X 0 das Spiegelbild S(AB) (X) von X bezüglich (AB). Der Fall
X = X 0 wird ausgeschlossen, da keine weiteren Fixpunkte abseits von (AB) existieren.
Daher muss die zweite Möglichkeit gelten, d.h. X 0 = S(AB) (X) für jeden Punkt X.
2.4
Beispiel 7: Kongruenzabbildung mit einem Fixpunkt
Aufgabenstellung
Gegeben sei eine Kongruenzabbildung T mit genau einem Fixpunkt O.
Zu zeigen: T ist eine Drehung um O.
Beweis
Zuerst wird ein Punkt A 6= O betrachtet, so dass A0 = T (A) 6= A gilt. Weiter ist |OA0 | =
|O0 A0 | = |OA|. Mit ϕ wird der (orientierte) Winkel ∠AOA0 6= 0◦ bezeichnet, der als
9
Drehwinkel bei der Drehung Dϕ um den Drehpunkt O dient. Per Definition gilt: Dϕ (A) =
A0 = T (A). Daraus folgt also, dass die inverse Drehung Dϕ−1 = D−ϕ die Bedingung
D−ϕ (A0 ) = A erfüllt. Aufgrund dessen wird die die Verkettung T1 = Dϕ−1 ◦ T untersucht.
T kann man dann auch als Gleichung schreiben.
T = Dϕ ◦ Dϕ−1 ◦ T = Dϕ ◦ T1
|
{z
T1
(2.2)
}
Weiter gilt: T1 (O) = O und T1 (A) = D−ϕ (T (A)) = D−ϕ (A0 ) = A. Die Kongruenzabbildung T−1 besitzt also wenigstens zwei unterschiedliche Fixpunkte O und A. Nun sind die
gleichen beiden Fälle wie in Beispiel 5 möglich, d.h. entweder ist T1 = S(OA) oder T1 = id.
Für Fall 1 folgt aus (2.2) T = Dϕ ◦ S(OA) , diese Abbildung hat jedoch noch weitere Fixpunkt (denn sie ist sogar eine Achsenspiegelung → Vgl. Affine Abbildungen) und kann
somit ausgeschlossen werden.
Für den zweiten Fall T1 = id folgert man T = Dϕ ◦id = Dϕ , was zeigt, dass die Abbildung
T eine Drehung um den Fixpunkt O ist.
Abbildung 2.1: Dϕ ◦ S(OA) ist eine Achsenspiegelung
2.5
Beispiel 8: Translation oder Gleitspiegelung
Begriffserklärung:
Translation = Parallelverschiebung;
Gleitspiegelung = Kombination aus Translation und Achsenspiegelung;
Aufgabenstellung
Sei T eine Kongruenzabbildung ohne Fixpunkt. Man bezeichne X als einen beliebigen
−−→
Punkt in R2 mit dem Vektor OX, wobei O der Ursprung ist.
Man beweise folgende Aussage: T ist entweder
eine Translation dann gilt: ∃ Vektor d : T (X) = X + d für jeden Punkt X, oder
10
eine Gleitspiegelung dann gilt: T (X) = Sg (X) + p für jeden Punkt X, wobei der Translationsvektor p parallel zur Achse g ist.
Beweis
−−→
O0 sei das Bild von O unter T und d = OO0 . Man betrachte die Parallelverschiebung Pd ,
wobei Pd (O) = O0 = T (O) gilt. Die Verkettung T2 = P−d ◦ T hat daher wenigstens einen
Fixpunkt, zumal T2 (O) = P−d (T (O)) = P−d (O0 ) = O ist.
Daraus ergeben sich drei Ansätze, die untersucht werden müssen:
1. Wenn T2 genau einen Fixpunkt hat, so handelt es sich bei T2 von einer Drehung um
O, also T2 = Dϕ .
2. Wenn T2 wenigstens zwei Fixpunkte O und A hat, aber nicht alle Punkte Fixpunkte
sind, so handelt es sich bei T2 von einer Geradenspiegelung S(OA) (Vgl. Beispiel 6).
3. Die letzte Möglichkeit ist, dass T2 = id.
T wird auch durch T = Pd ◦ (Pd−1 ◦ T ) = Pd ◦ T2 gegeben. Nun untersuche man die drei
|
{z
T2
}
Fälle.
1. Sei T = Pd ◦ Dϕ mit ϕ 6= 0, dann besitzt T einen Fixpunkt, wie man der Abbildung
entnehmen kann, hier ist es der Punkt Dϕ (X).
Abbildung 2.2: Pd ◦ Dϕ hat einen Fixpunkt
2. Sei nun T = Pd ◦ S(OA) und d senkrecht auf (OA), dann hat T Fixpunkte. Hierbei
sind nämlich alle Punkte der Geraden g1 = (OA) −
d
2
Fixpunkte von T . Ist jedoch
−−−→
d nicht orthogonal zu (OA), d.h. es tritt d = d1 + d2 , wobei d1 = α(OA) und
−−−→
d2 ⊥ (OA) gilt, in Kraft, so hat die Verknüpfung Pd ◦ S(OA) keinen Fixpunkt (Vgl.
Abbildung 2.3). Es findet hierbei eine Parallelverschiebung (Translation) der Punkte
X zu (OA) statt.
11
Abbildung 2.3: Pd ◦ S(OA) hat keinen Fixpunkt
T wird in diesem Fall als Gleitspiegelung Sg (X) + p mit p = d1 bezeichnet. g ist
das Bild der Geraden (OA) bei der Parallelverschiebung um den Vektor − d2 (Vgl.
Abbildung 2.4).
Abbildung 2.4: Pd ◦ S(OA) als Gleitspiegelung
3. Sei T2 gleich der Identitätsabbildung, so erhält man, dass die Kongruenzabbildung
T gleich der Translation Pd ist, da T2 = Pd ◦ id = Pd .
Der folgenden Tabelle kann man eine Klassifizierung der Kongruenzabbildungen im R2
entnehmen:
Fixpunkte
gleichsinnig
gegensinnig
Keine
Translation
Gleitspiegelung
Genau einer
Drehung
–
Genau eine Gerade
–
Achsenspiegelung
Identitätsabbildung
–
2
R
12
2.6
Beispiel 9: Geraden mit Schnittpunkt
Aufgabenstellung
1. Gegeben seien zwei Geraden g1 und g2 , die sich im Punkt O schneiden, und ein
gerichteter Winkel ϕ, der zwischen den beiden Geraden aufgespannt wird.
Zu zeigen ist, dass die Verkettung T = Sg2 ◦ Sg1 die Drehung um O mit dem Drehwinkel 2ϕ darstellt, also T = Sg2 ◦ Sg1 = Dϕ (O).
2. Nun seien drei Geraden g1 , g2 und g3 gegeben. Die Geraden nennt man konkurrent,
da sie sich in einem gemeinsamen Punkt O schneiden. Mit Sj = Sgj mit j = 1, 2, 3
wird die Achsenspiegelung an gj bezeichnet.
Zu zeigen ist die Relation (S3 ◦ S2 ◦ S1 ) ◦ (S3 ◦ S2 ◦ S1 ) = id.
Beweis
1. Die Komposition T = Sg2 ◦Sg1 bildet eine gleichsinnige Kongruenzabbildung mit dem
Fixpunkt O ab, d.h. T ist eine Drehung um O. Zur Bestimmung des Drehwinkels,
muss ein Punkt A ∈ g1 betrachtet werden. Da A0 = Sg1 = A und A00 = T (A) =
Sg2 (A0 ) = Sg2 (A), wird der Drehwinkel durch ∠AOA00 = 2∠(g1 , g2 ) = 2ϕ festgelegt.
2. Man fasse die Verkettung S3 ◦ S2 ◦ S1 als T zusammen, wobei T eine gegensinnige
Kongruenzabbildung mit dem Fixpunkt O ist (Vgl. Abbildung 2.5), damit folgt auch
das T eine Achsenspiegelung ist.
⇒ T 2 = T ◦ T = id
Abbildung 2.5: Verkettung dreier Achsenspiegelungen an konkurrenten Geraden
13
2.7
Beispiel 10: Satz von Napoleon
Aufgabenstellung
Es sei ein Dreieck ABC gegeben. Durch Spiegelung an BC, CA und AB konstruiere man
von ABC aus nach außen gerichtete, gleichseitige Dreiecke BCA0 , CAB 0 bzw. ABC 0 . Man
bezeichne die Mittelpunkte dieser Dreiecke mit X, Y bzw. Z.
Zu zeigen ist, dass das Dreieck XY Z gleichseitig ist.
Abbildung 2.6: Grundkonstruktion
Abbildung 2.7: Mit Hilfsstrecken
Beweis
Zuerst werden die Drehungen um X, Y und Z, jeweils mit dem Drehwinkel 120◦ , betrachtet. Hierbei wird der Punkt Z 0 , der die Eigenschaft besitzt, dass ∠Z 0 XY = 60◦ = ∠XY Z 0
(was impliziert, dass das Dreieck XY Z 0 gleichseitig ist), bezeichnet. Die Aufgabe lautet
nun zu zeigen, dass Z 0 = Z gilt. Weiter wird eine Verkettung T := DY ◦ DX definiert, die
eine Drehung um Z 0 mit dem Drehwinkel 120◦ + 120◦ = 240◦ (oder −120◦ ) darstellt. Man
nehme an, dass Z 0 6= Z ist. Für die Komposition gilt dann:
T1 = DZ ◦ DY ◦ DX = DZ,120◦ ◦ DZ 0 ,240◦
Somit ist die Verkettung eine Translation, da für die Winkel die erforderliche Relation
120◦ + 240◦ = 360◦ erfüllt ist. Es gilt jedoch auch T1 (B) = B, was bedeutet, dass T1 einen
Fixpunkt hat. Hieraus folgt ein Widerspruch zur gestellten Annahme Z 0 6= Z. Also muss
Z 0 = Z und damit ist auch das Dreieck 4XY Z gleichseitig.
14
2.8
Beispiel 11: Kollineare Mittelpunkte
Aufgabenstellung
Durch ABC und A0 B 0 C 0 seien zwei kongruente Dreiecke geben. Hierbei ist das Dreieck
ABC negativ und das Dreieck A0 B 0 C 0 positiv orientiert.
Zu zeigen: Die Mittelpunkte A00 , B 00 und C 00 der Strecken (AA0 ), (BB 0 ) und (CC 0 ) bilden
eine Gerade (sind also kollinear).
Beweis
Die Dreiecke ABC und A0 B 0 C 0 sind zwar kongruent, jedoch gegensinnig orientiert, somit
existiert eine gegensinnige Kongruenzabbildung T mit T (ABC) = A0 B 0 C 0 . Daraus resultieren zwei mögliche Optionen, entweder ist T = Sg eine Geradenspiegelung oder T = Sg,d
eine Gleitspiegelung mit einer Achse g. Für beide Möglichkeiten gilt für jeden Punkt X,
dass der Mittelpunkt X 00 der Strecke XX 0 (wobei X 0 = T (X) ist) auf der Achse g liegt.
Damit gilt auch A00 , B 00 , C 00 ⊂ g.
Abbildung 2.8: Gegensinnig kongruente Dreiecke
15
Kapitel 3
Schließungssätze
Schließungssätze behandeln Streckenzüge, die nach bestimmten Regeln und Vorgaben
konstruiert werden. Sie haben die besondere Eigenschaft, dass sie nach einer bestimmten
Anzahl von Strecken schließen.
3.1
Beispiel 12: Ente schwimmt im Teich
Aufgabenstellung
Um einen runden Teich sind drei gerade Wege l1 , l2 und l3 angelegt. Eine Ente, die einen
Hang zur mathematischen Fortbewegung hat, startet am Ufer an einem beliebigen Punkt
A0 und schwimmt parallel zu l1 bis sie wieder am Ufer ankommt, dieser Punkt wird mit
A1 bezeichnet. Von diesem Punkt setzt sie ihren Weg fort, in dem sie neben l2 wieder in
Richtung Ufer (Punkt A2 ) schwimmt. So schwimmt sie weiter parallel zu l3 ans Ufer, dann
wieder zu l1 , dann zu l2 und schließlich wieder zu l3 bis sie den Endpunkt A6 erreicht.
Zu zeigen ist nun, dass A6 dem Anfangspunkt A0 entspricht.
Abbildung 3.1: Der Weg der Ente
Beweis
Man konstruiere zuerst die Senkrechten gj , j = 1, 2, 3, zu lj durch den Mittelpunkt des
16
Teichs, der auch der Schnittpunkt der Geraden g1 , g2 und g3 ist, somit sind sie auch
konkurrent. Die Mittelsenkrechten jeder Kreissehne durchlaufen den Kreismittelpunkt,
deshalb enthalten die Sehnen A0 A1 , A1 A2 , A2 A3 , A3 A4 , A4 A5 und A5 A6 jeweils die Mittelsenkrechten g1 , g2 , g3 , g1 , g2 und g3 .
⇔ A1 = S1 (A0 ), A2 = S2 (A1 ), A3 = S3 (A2 ), A4 = S1 (A3 ), A5 = S2 (A4 ), A6 = S3 (A5 )
mit Sj = Sgj , j = 1, 2, 3. Sj ist hierbei die Achsenspiegelung bezüglich gj . Damit kann
man A6 auch anders auffassen:
A6 = S3 ◦ S2 ◦ S1 ◦ S3 ◦ S2 ◦ S1 (A0 ) = id(A0 ) = A0
Teil (b) des Beispiels 9 impliziert, dass die Verknüpfung gleich der Identität von A0 ist.
3.2
Beispiel 13: Thomsenstreckenzug
Aufgabenstellung
Gegeben seien ein Dreieck ABC und die Punkte Ci ∈ (AB), Ai ∈ (BC), Bi ∈ (CA) für
i = 1, 2. Wobei folgende Eigenschaften gelten:
(A1 B1 ) k (AB), (B1 C1 ) k (BC), (C1 A2 ) k (CA), (A2 B2 ) k (AB), (B2 C2 ) k (BC)
Zu zeigen ist, dass auch (C2 A1 ) parallel zu (CA) ist.
Abbildung 3.2: Thomsenstreckenzug
Beweis
Mithilfe der Voraussetzung erhält man vier Parallelogramme:
A1 B1 C1 B, B2 AC1 A2 , B1 C1 A2 C, B2 C2 BA2
−−−−→ −−−−→
−−−→ −−−−→ −−−→
⇒ (A1 B) = (B1 C) und (C2 B) = (B2 A2 ) = (AC1 )
B1 AC1 = T−−−−→ A1 C2 B impliziert, dass man auch das Dreieck B1 AC1 aus dem Dreieck
(A1 B1 )
−−−→
A1 C2 B durch Translation von A1 B1 erhält.
−−−→
−−−−→
⇒ (B1 A) = T−−−−→ (A1 C2 ) und damit gilt: (C2 A1 ) k (CA)
(A1 B1 )
17
Kapitel 4
Literaturverzeichnis
[1] Lösungsstrategien – Mathematik für Nachdenker, Natalia Grinberg, 2011, S. 85 – 102
[2] http://www.cip.ifi.lmu.de/ grinberg/Dreigeom/SchlEG.pdf (Stand: 16.06.2015)
18