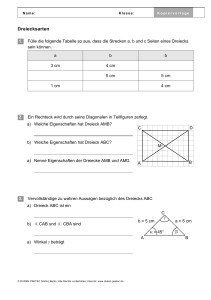
Satz 4. In einem stumpfwinkligen Dreieck ∆ABC liegt der

Satz 4. In einem stumpfwinkligen Dreieck ∆ABC liegt der Umkreismittelpunkt U außerhalb des Dreiecks.
Beweis. Wir beweisen indirekt, also: Wenn U innerhalb von ∆ABC liegt, dann ist
∆ABC spitzwinklig.
B
b
kU
a
U
c
ψ
b
φ
χ
α2
b
α α1
b
b
A
C
Die drei Winkel φ, χ, ψ sind jeweils Innenwinkel eines Dreiecks und daher mit Sicherheit kleiner als 180◦ . Wir erhalten daher:
χ + ψ > 180◦
(1)
Weil U Umkreismittelpunkt von ∆ABC ist, gilt AU = CU , das Dreieck ∆ACU ist
also gleichschenklig. Analog erfahren wir, dass ∆BAU gleichschenklig ist und erhalten
damit nach dem Innenwinkelsummensatz:
χ
180◦ − χ
= 90◦ −
2
2
180◦ − ψ
ψ
◦
α2 =
= 90 −
2
2
α1 =
(2)
(3)
Und natürlich:
α = α1 + α2
χ+ψ
α = 180◦ −
2
⇔
Womit zusammen mit Gleichung (1) natürlich folgt, dass α < 90◦ . Analog können wir
schließen, dass auch
β < 90◦
γ < 90◦
Das Dreieck ∆ABC ist also spitzwinklig.