rechnungen (application/pdf 3.3 MB)

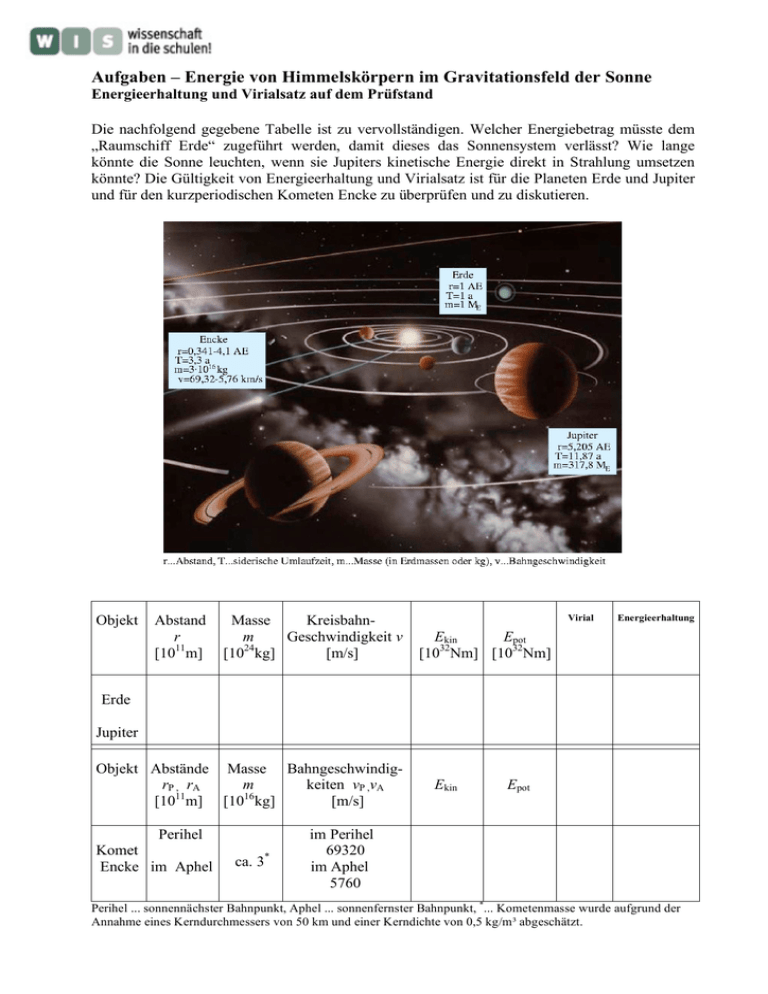
Aufgaben – Energie von Himmelskörpern im Gravitationsfeld der Sonne
Energieerhaltung und Virialsatz auf dem Prüfstand
Die nachfolgend gegebene Tabelle ist zu vervollständigen. Welcher Energiebetrag müsste dem
„Raumschiff Erde“ zugeführt werden, damit dieses das Sonnensystem verlässt? Wie lange
könnte die Sonne leuchten, wenn sie Jupiters kinetische Energie direkt in Strahlung umsetzen
könnte? Die Gültigkeit von Energieerhaltung und Virialsatz ist für die Planeten Erde und Jupiter
und für den kurzperiodischen Kometen Encke zu überprüfen und zu diskutieren.
Objekt
Abstand
r
[1011m]
Masse
Kreisbahnm
Geschwindigkeit v
[1024kg]
[m/s]
Virial
Energieerhaltung
Ekin
Epot
32
[10 Nm] [1032Nm]
Erde
Jupiter
Objekt Abstände Masse BahngeschwindigrP , rA
m
keiten vP ,vA
[1011m] [1016kg]
[m/s]
Perihel
Komet
Encke im Aphel
ca. 3*
Ekin
Epot
im Perihel
69320
im Aphel
5760
Perihel ... sonnennächster Bahnpunkt, Aphel ... sonnenfernster Bahnpunkt, *... Kometenmasse wurde aufgrund der
Annahme eines Kerndurchmessers von 50 km und einer Kerndichte von 0,5 kg/m³ abgeschätzt.
Lösungen zu den Aufgaben
Gravitationskonstante
= 6,6726·10-11 kg-1m3 s-2
Astronomische Einheit
1 AE = 1,496·1011 m
Erdmasse
ME = 5,979·1024 kg
Sonnenmasse
MS = 1,989·1030 kg
siderisches Jahr
1 a = 3,1558·107 s
Leuchtkraft der Sonne
LS = 3,846·1026 W
weitere geg. Größen siehe Abbildung
Geg.:
Lös.:
Objekt
Abstand
r
[1011m]
Masse
Kreisbahnm
Geschwindigkeit v
[1024kg]
[m/s]
Virial
Energieerhaltung
Ekin
Epot
Ekin/Epot
32
32
[10 Nm] [10 Nm]
Epot+Ekin
[1032Nm]
Erde
1,496
5,979
29785
26,521
-53,042
-0,5
-26,521
Jupiter
7,787
1900,13
13061
1620,7
-3238,4
-0,5
-1620,7
Objekt Abstände Masse BahngeschwindigrP , rA
m
keiten vP , vA
Ekin
11
16
[10 m] [10 kg]
[m/s]
[1025Nm]
Perihel
Komet
0,510
Encke im Aphel
6,134
ca. 3
im Perihel
69320
im Aphel
5760
Epot
Ekin/Epot
25
[10 Nm]
Epot+Ekin
[1025Nm]
7,208
-7,807
-0,923
-0,599
0,0498
-0,649
-0,077
-0,599
Die Erde verlässt den Einflussbereich der Sonne, wenn sie ihre Bindung zur Sonne verliert, d. h.
wenn ihr der Betrag ihrer Bindungsenergie (Epot) zugeführt wird. Dieser beträgt
E pot =
−γ ⋅ MS ⋅m
r
− 6,6726 ⋅ 10 −11 m 3 ⋅ 1,989 ⋅ 10 30 kg ⋅ 5,979 ⋅ 10 24 kg
=
= −53,042 ⋅ 10 32 Nm.
2
11
kg s
1,496 ⋅ 10 m
Die Sonne könnte vom kinetischen Energievorrat Jupiters etwa 13 Jahre leuchten, was sich
einfach aus dem Quotienten von kinetischer Energie und Strahlungsleistung ergibt.
t=
E kin
LS
=
1620,7 ⋅10 32 Nm ⋅ s
≈ 4,2 ⋅10 8 s ≈ 13 a.
26
3,846 ⋅10 Nm
Der Energieerhaltungssatz der Mechanik besagt eigentlich, dass die kinetischen Energien und
die potentielle Energie aller Körper des Sonnensystems (als abgeschlossenes System) in ihrer
Summe erhalten bleiben. Dabei ist berücksichtigt, dass dies für einen einzeln betrachteten
Körper (z. B. einen Kometen) nicht gelten muss, da er ja Energie „tanken“ kann, wenn er z. B.
dicht an Jupiter vorbeifliegt. Für die folgende Rechnung werden solche Wechselwirkungen
ausgeschlossen. Die Energieerhaltung wie auch der Virialsatz gelten dann für jedes einzelne
Objekt (Vereinfachung). Der Energieerhaltungssatz lautet
E kin + E pot = E = konstant,
m 2
1
⋅ v − γ ⋅ M S ⋅ m ⋅   = konstant.
2
r
Für die Kreisbahnen der Planeten (Ellipsenform fast nicht wahrnehmbar) ist der Wechsel
zwischen potentieller und kinetischer Energie von vornherein ausgeschlossen, so dass die
Energie sogar in ihren Formen erhalten bleibt. Bemerkenswert ist lediglich, dass die
Gesamtenergie E eines Himmelskörpers auf einer Kreisbahn jeweils gerade seiner negativen
kinetischen Energie entspricht. Auf der lang gestreckten Ellipsenbahn des Kometen Encke
kommt es dagegen zu einem deutlichen Austausch zwischen den beiden Energieformen. Im
folgenden werden die Energien in den Extrempunkten der Kometenbahn (rP...Perihel und
rA...Aphel) berechnet und in ihrer jeweiligen Summe miteinander verglichen.
Encke im Perihel : E P =
1
m 2
⋅ vP − γ ⋅ M S ⋅ m ⋅  
2
 rP 
2
3 ⋅ 1016 kg 
m
m 3 1,989 ⋅ 10 30 kg ⋅ 3 ⋅ 1016 kg
=
⋅  69320  − 6,6726 ⋅ 10 −11
⋅
≈ −0,599.
2
s
kg s 2
0,51 ⋅ 1011 m

Encke im Aphel :
EA =
1
m
2
⋅ vA − γ ⋅ M S ⋅ m ⋅  
2
 rA 
2
3
3 ⋅ 1016 kg 
m
1,989 ⋅ 10 30 kg ⋅ 3 ⋅ 1016 kg
−11 m
=
⋅  5760  − 6,6726 ⋅ 10
⋅
≈ −0,599.
2
s
kg s 2
6,134 ⋅ 1011 m

Mit EP = EA ist die Energieerhaltung bewiesen.
Die Gültigkeit des Virialsatzes lässt sich für die Planeten schnell ersehen, da die berechneten
Werte für Ekin und Epot zugleich ihren zeitlichen Mittelwerten entsprechen.
1
E kin = − E pot
2
Erde :
E kin
Jupiter :
E kin
E pot
E pot
⇒
E kin
E pot
1
=− ,
2
=
26,521 ⋅ 10 32 Nm
≈ −0,5,
- 53,042 ⋅ 10 32 Nm
=
1620,7 ⋅ 10 32 Nm
≈ −0,5.
- 3238,4 ⋅ 10 32 Nm
Im Falle der Ellipsenbahn des Kometen Encke weichen die Werte für das Virial bei
Momentaufnahmen der Bahn wie zu erwarten stark von -0,5 ab.
Encke im Perihel :
E kin
Encke im Aphel :
E kin
E pot
E pot
=
7,208 ⋅ 10 25 Nm
≈ −0,923,
- 7,807 ⋅ 10 25 Nm
=
0,0498 ⋅ 10 25 Nm
≈ −0,077.
- 0,649 ⋅ 10 25 Nm
Ein zeitlich gemitteltes Virial lässt sich erhalten, wenn man die Energien nach ihrer zeitlichen
Häufigkeit in die Rechnung eingehen lässt. Im Perihel läuft der Komet sehr schnell und
entsprechend wird ein sehr kurzer Bahnabschnitt (für den das Viral konstant sein soll) auch
schnell durchlaufen (kleines zeitliches Gewicht). Im Aphel dagegen ist der Komet um den
Faktor, der dem Verhältnis der Bahngeschwindigkeiten (vP / vA) entspricht, länger auf diesem
Bahnstück unterwegs (großes zeitliches Gewicht). Die entsprechende Rechnung ergibt:
E kin
E pot
=
7,208 ⋅ 10 25 Nm + (69320 / 5760) ⋅ 0,0498 ⋅ 10 25 Nm
≈ −0,5.
- 7,807 ⋅ 10 25 Nm + (69320 / 5760) ⋅ - 0,649 ⋅ 10 25 Nm