29 Elektromagnetische Wellen 2
Werbung
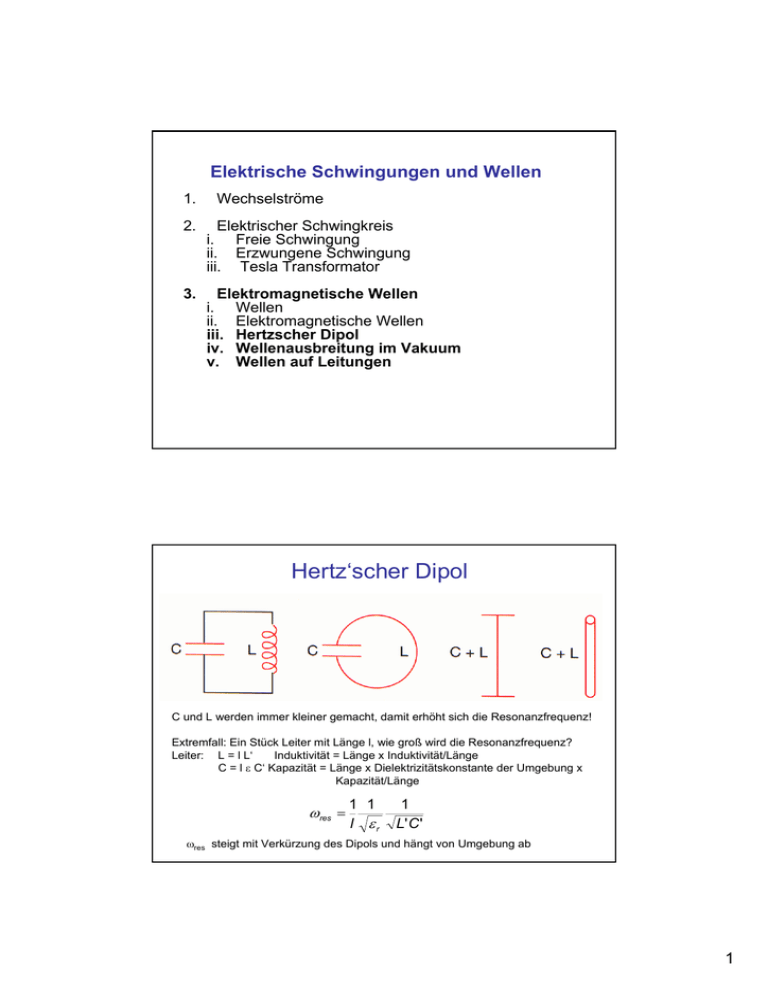
Elektrische Schwingungen und Wellen 1. Wechselströme 2. Elektrischer Schwingkreis i. Freie Schwingung ii. Erzwungene Schwingung iii. Tesla Transformator 3. Elektromagnetische Wellen i. Wellen ii. Elektromagnetische Wellen iii. Hertzscher Dipol iv. Wellenausbreitung im Vakuum v. Wellen auf Leitungen Hertz‘scher Dipol C und L werden immer kleiner gemacht, damit erhöht sich die Resonanzfrequenz! Extremfall: Ein Stück Leiter mit Länge l, wie groß wird die Resonanzfrequenz? Leiter: L = l L‘ Induktivität = Länge x Induktivität/Länge C = l ε C‘ Kapazität = Länge x Dielektrizitätskonstante der Umgebung x Kapazität/Länge ωres = 1 1 l εr 1 L' C ' ωres steigt mit Verkürzung des Dipols und hängt von Umgebung ab 1 Feldverteilung L und C: Felder konzentriert auf Inneres der Spule bzw Kondensator außerhalb der Elemente Felder ~ 0 Hetzscher Dipol: Felder reichen weit nach außen Umgebung spürt Felder Feldverteilung eines Dipols Die in der ersten Schwingungsperiode erzeugten E- und B-Felder breiten sich im Raum aus, dann wechseln die Vorzeichen und die äußeren Feldbereiche schnüren und koppeln sich ab (Seifenblase!) Energie wird abgestrahlt: Schwingkreis wird gedämpft 2 Abstrahlung Hertz‘scher Dipol Felddarstellung: elektrisches Feld Abstrahlung Hertz‘scher Dipol Poynting Darstellung: Punktdichte prop zu Energie 3 Erzwungene Schwingung Ohmsche Verluste in Leiter und angestrahlte Energie dämpfen Schwingkreis Aufrechterhaltung durch Wechselspannugsquelle Resonanz Damit vom Sender effektiv Energie abgestrahlt werden kann, muss er in Resonanz mit dem Dipol sein. Resonanzbedingung: Wellenlänge muss gleich 2 l sein Stationäre Strom und Spannungsverteilung Randbedingung: offenes Ende Strom muss null werden maximale Spannung zwischen Enden Experiment: Wellenlänge λ = 2,4 m ⇒ Dipollänge =1,2m 4 Nachweis der Verteilung Schleife mit Glimmlampe Nachweis von B bzw I Entladungslampe Nachweis von E bzw U Spannung auf Leiter hängt vom Ort ab!!! Stehende Welle Hertzscher Dipol Nachweis von Strom Elektrischer Sender ≈ Optimaler Empfang, wenn Empfänger und Sender in Resonanz ωres = Sendedipol Empfangsdipol Erzwungene Schwingung Sendedipol f = 125MHz λ = c/f = 2.4m Wellenlänge 1 1 l εr 1 L' C ' Abstimmung über Länge Empfänger = Sender oder Dielektrizitätskonstante 5 Hertzscher Dipol in Wasser Optimaler Empfang, wenn Empfänger und Sender in Resonanz ωres = 1 1 l εr 1 L' C ' Abstimmung über Länge: Optimum Länge Empfänger = Länge Sender Aber Länge hängt auch von Eigenschaften des umgebenden Medium ab: Wasser: εr = 81 Verhältnis Dipollänge Luft : Dipollänge Wasser = 1 : √εr = 1 : 9 Abstrahlcharakteristik eines Dipols In welche Richtung strahlt ein Dipol ab? θ Die maximale Abstrahlung erfolgt normal zur Dipolachse Keine Abstrahlung in Richtung der Dipolachse P(θ) prop sin(θ)2 6 Polarisation Ausbreitungsrichtung Polarisation gibt die Richtung des elektrischen Feldes an Dipol: E parallel zu Stabachse und daher normal auf Ausbreitungsrichtung Nachweis: Empfangsdipol nur empfangsfähig, wenn Stabachse parallel zu Polarisationsrichtung, d.h. Richtung des E Feldes + Hertzscher Dipol mikroskopisch + + Schwerpunkt +q Auslenkung d Schwerpunkt -q Ortsfeste positive Kerne Frei bewegliche Elektronen Neutrales Metall: Ladungsschwerpunkte gleich Zeitabhängiges Dipolmoment Wechselfeld ( E0sin(ωt) ) angelegt: Elektronen schwingen relativ zu Kernen Ladungsschwerpunkte verschoben Beschreibung mit Dipolmoment p = q d0 r r r p(t ) = qd (t ) = qd 0 sin ωt ez Wie groß ist max. Auslenkung d0? Weg nach viertel Periode T: d = v T/4 v Driftgeschwindigkeit << c v ≈1m/s, f = 10MHz ⇒ T= 0.1µs: d0 = 4 10-8 m Antennenlänge l = λ/2= c T/2 = 15m >> d0 7 Theorie des Hertzschen Dipols Allgemein: zeitabhängige Strom- und Ladungsverteilung Berechnung von Potenzial bzw. Vektorpotenzial als Funktion von Ort und Zeit, B und E daraus berechnen r12 r2 0 Leiter mit Ladungsdichte ρ P Wechselstrom Oszillationen Stromdichte j = ρ v Stromdichte verknüpft mit Vektorpotenzial A Vektorpotenzial in P gegeben r r r1 r r j (r ) A(r1 ) ∝ ∫ 2 dV2 Stationäre Stromdichte r12 Zeitliche Änderung des Stroms in r2 wird in r1 nur verzögert wahrgenommen EM Welle breitet sich mit Lichtgeschwindigkeit aus Vektorpot zum Zeitpunkt t wird von Stromdichte zu Zeitpunkt t-∆t bestimmt ∆t = Abstand/ Lichtgeschwindigkeit = r12/c = Retardierung r r r r j (r , t − r12 / c ) A(r1, t ) ∝ ∫ 2 dV2 r12 Theorie des Hertzschen Dipols r r r r j (r , t − r12 / c ) A(r1, t ) ∝ ∫ 2 dV2 r12 Ladungen schwingen mit Frequenz ω dp = qv dt r r cos(ωt − kr ) ω Zeitlich veränderliches Vektorpot, ⇒ A(r1, t ) ∝ qd 0ω k= r c das sich mit Lichtgeschwindigkeit ausbreitet Aus Vektorpot folgen zwei Terme: Nahfeld von E und B: r12 ≈ Wellenlänge Fernfeld von E und B: r12>> Wellenlänge Nahfeld: Magnetfeld durch Strom Woher kommen die? im Dipol erzeugt ∂E rotB = µ0 j + µ 0ε 0 Fernfeld: Magnetfeld durch ∂t Verschiebungsstrom mit j = vρ ∫ ρdV = q sowie p(t ) = p0 sin ωt und E im Nahfeld durch Ladungsverteilung (Quellenfeld) E im Fernfeld durch Induktion dB/dt (Wirbelfeld) 8 Ergebnisse Fernfeld 1. E und B in Phase 2. B konzentrische Kreise um Dipolachse, E immer senkrecht auf B und senkrecht auf Abstandsvektor zum Mittelpunkt 3. E = c B (EM Wellen) 4. In großem Abstand B und E näherungsweise linear polarisierte ebene Wellen, Ebene senkrecht durch Zentrum 5. Abgestrahltes Feld proportional zu Dipolbeschleunigung, Amplitude nimmt mit 1/r ab (Kugelwelle) &&(r , t ) 1 ∂2 p E ∝B∝ p(r , t ) = 2 r ∂t r 1 p0ω 2 E = sin(θ ) sin(ωt − kr ) 4πε 0c 2 r Hertzscher Dipol Abstrahleigenschaften Energiestromdichte Poynting Vektor r 1 r r 1,0 S= E ×B µ0 θ 30 0,8 0,6 Betrag der mittleren Dichte 0,4 r sin2 θ 2 0,2 S ∝ p0 ω 4 r2 0,0 Gesamte abgestrahlte Leistung 0,2 p0 ω 4 12πε 0c 3 2 P= 0 330 r S 300 60 270 90 0,4 0,6 240 120 0,8 1,0 210 Folgerungen: 1) Abstrahlungscharakteristik eines Dipols: ∝ sin2θ Keine Abstrahlung in Richtung des Dipols 2) Abstandsgesetz: S ∝1/r2(Energieerhaltung) 3) Frequenzabhängigkeit: ∝ ω4, 1/λ4 Beispiel: Himmelsblau ("Rayleigh –Streuung") 150 180 9 Abstrahlung einer beschleunigten Ladung Theorie: Jede beschleunigte Ladung strahlt wie ein Dipol eine elektromagnetische Welle ab. Gesamte abgestrahlte Leistung proportional zum Quadrat der Beschleunigung P= 2e 2 ⎛ dv ⎞ ⎜ ⎟ 3εc 3 ⎝ dt ⎠ 2 Harmonisch bewegte Ladung: Definition eines „Dipolmoments“ p(t) = p0 sin(ωt) = e x0 sin(w t) Beschleunigung = d2 p(t)/dt2 P= 2 p02ω 4 3εc 3 Abstrahlcharakteristik wie bei Dipolstrahlung Abstrahlung einer beschleunigten Ladung Jede beschleunigte Ladung strahlt Energie ab Was heisst beschleunigt? Beispiel: Lineare Teilchenbeschleuniger (LINAC Stanford) Elektron gewinnt in einem Meter eine kinetische Energie von 10MeV Abgestrahlte Leistung P ~ 10-40 (10 MV)2 = 10-26 W so gut wie nichts verlustfrei Damit Leistung abgestrahlt wird, müsste Energie um 1014 MeV pro Meter erhöht werden Makroskopisch beschleunigte Teilchen strahlen offensichtlich nicht Welche dann? 10 Röntgenröhre Elektronen in E-Feld beschleunigt Auftreffen an Anode: Kollision mit Atomen Abbremsung (negative Beschleunigung) Emission von EM Welle Elektronen stoßen nicht mit Atomen zusammen, sondern werden abgelenkt Synchrotron Synchrotrons: Elektronen laufen mit nahezu Lichtgeschwindigkeit auf Kreisbahn Um Elektronen auf Kreisbahn zu halten ist Zentripetalbeschleunigung erforderlich 11 Synchrotronstrahlung Elektronen auf Kreisbahn Geschwindigkeit konstant aber Richtung wird geändert (Zentripetalbeschleunigung) Durch relativistische Effekte Abstrahlung in Bündel in Richtung der Geschwindigkeit Elektromagnetisches Spektrum Transversale EM Wellen Wellenlänge λ Frequenz f Lichtgeschwindigkeit c (2.998 108 m/s) λ= c f Vakuum 12 Mikrowellen Mikrowellen sind elektromagnetische Wellen Wellenlänge im cm bzw. mm Bereich Eignen sich gut zur Demonstration der Welleneigenschaften von elektromagnetischer Strahlung Mikrowellensender Dipol Mikrowellenempfänger Dipol (mit Lautsprecher verbunden) Absorption von Mikrowellen Messung der Transmission von Mikrowellen: Isolatoren: Kunststoff, Papier Metallen Wasser Eis Mikrowellen: Elektromagnetische Strahlung Dipole werden ausgerichtet Energieaufnahme: Resonanz Eis: Dipole fix keine Resonanz 10 GHz 13 Reflexion von Mikrowellen Empfänger Sender Mikrowellen werden reflektiert Einfallswinkel = Ausfallswinkel Polarisation E Feld Empfangsdipol orthogonal zu E Feld: kein Empfang Schlitze parallel zu E Feld: kein Empfang (vgl. Seilwelle) Schlitze normal zu E Feld Empfang (Seilwelle würde nicht druchgehen) Mikrowellen linear polarisierte EM Wellen 14 Brechung Bei Übergang von Medien, ändert EM Welle ihre Richtung Herleitung: Stetigkeitsbedingungen an Grenzflächen Wellenoptik mit Mikrowellen Mehrere Spalte: Intensität in Schattenraum und starke räumliche Modulation des Intensitätsverlaufs: Interferenz Mikrowellen zeigen Welleneigenschaften: Interferenz und Beugung 15 Stehende Wellen Empfänger Sender λ Welle wird an Metall reflektiert Phasengeschwindigkeit Metall < Luft π Phasensprung: Knoten an Metall Abstand zwischen zwei Maxima λ/2 (wg. Leistung ∝ E2) f = 10GHz ⇒ λ = 3cm Welleneigenschaften 1. Absorption: Welle wird beim Durchgang durch Medium abgeschwächt, Energie wird in Medium deponiert (Wärme) Absorption hängt von Material, Aggregatzustand, Frequenz, … ab 2. Reflexion: Welle dringt nicht in Medium ein, Energie wird in bestimmten Winkel reflektiert 3. Polarisation: EM Wellen sind polarisiert, Nachweis mit Orientierung des Dipols, bzw. Polarisator der nur eine Polarisationsrichtung durchlässt 4. Beugung: EM Welle gelangt in den Schattenraum von Hindernissen (die klein bzw. vergleichbar groß wie Wellenlänge sind) 5. Interferenz: EM Wellen überlagern sich, es kommt lokal zu Überhöhungen bzw. Auslöschungen (stehende Welle, Gitter..) 6. Brechung: EM weichen von geradliniger Ausbreitung ab 16 Wellenleiter Man kann Wellen auch in Hohlleitern (z.B. in Rohren) transportieren: Da das Material leitend ist, verschwindet die elektrische Feldstärke an den Rändern. Die Verwendung von Hohlleitern zum Energietransport ist der von normalen Drähten bei hohen Frequenzen deutlich überlegen: Es gibt keine Verluste durch den ohmschen Widerstand und durch die Abstrahlung von elektromagnetischen Wellen! Rechteckförmiger Wellenleiter: Hohlleiter E Feld Hohlleiter eignen sich nur für hohe Frequenzen > fgrenz fgrenz = c/ 2 a H- Feld 17 Kurzwellenübertragung Ionosphäre und Erde bilden Wellenleiter Kurzwellen können empfangen werden, wo sie durch geometrische Ausbreitung nicht erwartet werden können. Glasfaser 18 Drahtwellen Stehende Wellen auf offener Leitung Jede am Ende offene Leitung (Leerlauf) besitzt dort ein Spannungsmaximum und ein Stromminimum. 19 Kurzgeschlossene Leitung Jede am Ende kurzgeschlossene Leitung besitzt dort ein Strommaximum und ein Spannungsminimum. Lecherleitung Entlang von parallelen Drähten (Doppelleitung, Flachbandkabel) kann man elektromagnetische Wellen transportieren: Wenn der Drahtabstand d klein ist gegenüber der Wellenlänge λ interferieren die von beiden Leitern erzeugten elektromagnetischen Wellen destruktiv, so dass auch hier die Abstrahlungsverluste klein sind. Nachweis Spannung mit Glimmlampe Nachweis Strom Spule Die Ströme auf den beiden Leitern sind um 180° phasenverschoben, daher überlagern sich die abgestrahlten elektromagnetischen Wellen destruktiv. Ist das zweite Ende offen, gibt es dort Knoten in der Stromverteilung und Bäuche in der Spannungsverteilung. 20 Koaxialkabel Hier dient der äußere (geerdete) Mantel als Abschirmung. Die elektromagnetischen Wellen können nicht nach außen entweichen. Der Innenraum ist meist mit einem Dielektrikum ausgefüllt. 21