Der Dipol im elektrischen Feld - Hu

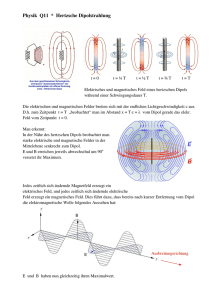
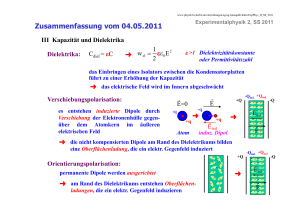
Der Dipol im elektrischen Feld
Der elektrische Dipol
+Q
+
−Q
−
r
l
r
r
Definition Dipolmoment: p = Q l
Die Kraft auf einen Dipol im elektrischen Feld
Allgemein gilt für die Kraftwirkung auf eine Verteilung von n Punktladungen im ortsabhängigen elektrischen Feld :
r n
r r r
F = ∑ q i ( ri )E( ri )
i =1
Für zwei Ladungen +Q und –Q im Abstand l gilt dann:
(
r
r r r r r
F = Q E( r ) − E( r + l )
r r r
r r
)
r r r
Mittels Taylorentwicklung E( r + l ) = E( r ) + ∇(E ⋅ l ) + ...
vereinfacht sich die Gleichung zu
r
r
r r r r r r
r r
∂E
F = Q ⋅ ∇(E ⋅ l ) = ∇(E ⋅ p) = grad(E ⋅ p) = p
∂l
Die Kraftwirkung auf einen Dipol ist somit proportional zum Gradienten des elektrischen Feldes in Richtung der Dipolachse und zum Dipolmoment.
Die potentielle Energie eines Dipols ergibt sich wegen
r
F = −gradE pot
und
( )
r
r r
F = grad E ⋅ p
zu
E pot
r r
= −E ⋅ p
Homogenes elektrisches Feld
r r
r r
E( r1 ) = E( r2 )
+
r
+ Q( r1 )
r
l
+
2
(
r
E0
SP
r
l
−
2
−
r
− Q( r2 )
)
r
r r r r r
F = Q E( r ) − E( r + l ) = 0
Der Schwerpunkt SP des Dipols bewegt sich nicht, aber wegen
r
r
r
r
r
F1 = −F2 = QE übt das Feld E ein Drehmoment D auf den Dipol aus:
r r r r
r r r
D = l × F = Ql × E = p × E
Das Drehmoment bewirkt, dass der Dipol in Feldrichtung orientiert
wird.
Inhomogenes elektrisches Feld
r r
r r
E( r1 ) ≠ E( r2 )
Wegen
r
r
r
r r r
r
∂E
=
⋅
=
≠0
F
grad
(
E
p
)
p
D = p × E ≠ 0 und
∂l
wirkt auf den Dipol ein Drehmoment und auf den Schwerpunkt des
Dipols eine resultierende Kraft. Dies führt zu folgenden Bewegungen:
• Der Dipol wird im Feld orientiert (Rotation)
• Der Dipol wird im Feld verschoben (Translation)
r r
E( r )
+Q
+
r
l
−Q
−
r
F
+
Der Dipol wird angezogen
(siehe Experiment: Ablenkung eines Wasserstrahles im elektrischen Feld)