Teil 4 - Institut für Physik

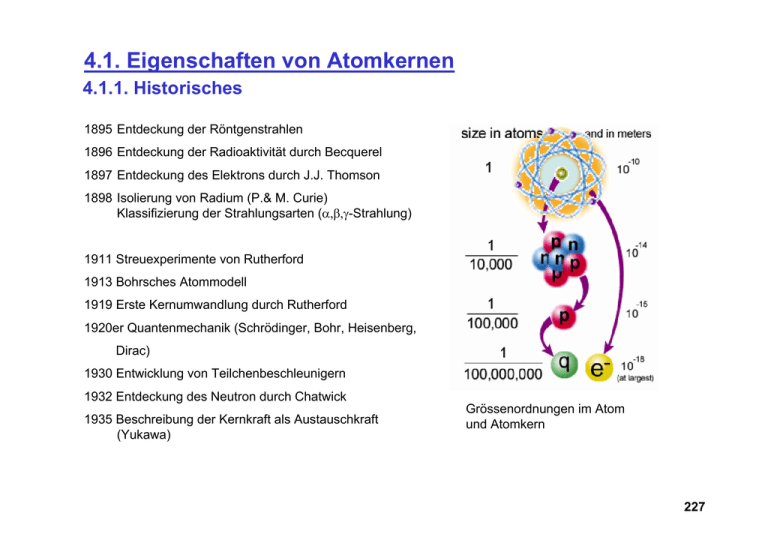
4.1. Eigenschaften von Atomkernen
4.1.1. Historisches
1895 Entdeckung der Röntgenstrahlen
1896 Entdeckung der Radioaktivität durch Becquerel
1897 Entdeckung des Elektrons durch J.J. Thomson
1898 Isolierung von Radium (P.& M. Curie)
Klassifizierung der Strahlungsarten (α,β,γ-Strahlung)
1911 Streuexperimente von Rutherford
1913 Bohrsches Atommodell
1919 Erste Kernumwandlung durch Rutherford
1920er Quantenmechanik (Schrödinger, Bohr, Heisenberg,
Dirac)
1930 Entwicklung von Teilchenbeschleunigern
1932 Entdeckung des Neutron durch Chatwick
1935 Beschreibung der Kernkraft als Austauschkraft
(Yukawa)
Grössenordnungen im Atom
und Atomkern
227
1936 Entdeckung des Myons
1938 Erste Kernspaltung
1939 Korrekte Deutung der Kernspaltung (Meitner, Frisch)
Erste Kernmodelle (Bohr, Wheeler)
1942 Erste kontrollierte Kettenreaktion (Fermi)
1945 Entwicklung der Atombombe
1950er Experimentelle Kernphysik mit Kernreaktoren,
theoretische Beschreibung der Kernkräfte
1956 Theorie des β-Zerfalls
Künstlerische Darstellung
des Atomkerns
1970er Experimentelle Kernphysik mit schweren Ionen
Streuexperimente mit hochenergetischen Teilchen erbrachten Aufschluss
über die Struktur des Atoms (und später auch) des Atomkerns.
Auch der Atomkern ist kein elementares Teilchen, sondern besitzt eine innere Struktur!
228
Die Streuexperimente von E. Rutherford (1911):
Atome haben einen schweren positiv geladenen Kern mit einem Radius von etwa
einen fm = 10-15 m
Streuereignisse selbst bei
grossen Winkeln!
Experiment nach Geiger und Marsden
229
4.1.2. Zusammensetzung der Kerne
Kerne sind nicht aus Elektronen und Protonen zusammengesetzt, (wie man zunächst dachte)!
Es existieren weitere Kernteilchen (Nukleonen)!
Entdeckung des Neutrons durch Chatwick (1932):
Neutrale Teichen (Neutronen) können aus einer Protonen-haltigen Folie Protonen
freisetzen. Diese können als geladene Teilchen ein Gas ionisieren.
Das Neutron ist ein elektrisch neutrales Teilchen der Masse:
230
Bezeichnungen:
Ordnungszahl, Atomladungszahl,
Kernladungszahl oder Protonenzahl
Z
Neutronenzahl
N
Massenzahl
A=Z+N
Spezifische Kerne bezeichnet man als Nuklide.
Nuklide mit gleicher Ordnungszahl Z aber unterschiedlicher Neutronenzahl N
bezeichnet man als Isotope.
Isotope des Wasserstoffs
231
Kernmassen
Die Kernmassen werden in der Kernphysik oft in der Masseneinheit u gemessen.
Die gemessene Masse von Kernen entspricht nicht der Summe der Massen ihrer
Protonen und Kerne:
Massendefekt
Der Massendefekt kommt durch die Bindungsenergie zustande. Nach der Relativitätstheorie:
Bindungsenergie
und:
Bindungsenergie pro Nukleon
beträgt typischerweise 6-8 MeV
232
Kernmassen können im Massenspektrometer durch Ablenkung in elektrischen und
magnetischen Feldern bestimmt werden:
Besonders genau ist die
relative Massenbestimmung
Δm/m=10-4
und:
Δm/mcal =10-8 (mcal =12C)
Massenspektrometer
58Fe
Gemessene Bindungsenergie pro
Nukleon.
Der stabliste Kern ist Eisen.
[aus Evans: Tipler Physik]
233
Kernradien
Kerne haben eine kompakte (nahezu) kugelförmige Gestalt, man kann einen
Kernradius bestimmen.
Kernradius = einige Femtometer (fm); 1 fm = 10-15 m
somit Kerndichte: ρ = 1014 g/cm3
Man erwartet eine Abhängigkeit der Form r = const. A1/3
Experimentelle Methoden zur Bestimmung des Kernradius:
Neutronenstreuung
Potential der Kernkräfte
Elektronenstreuung
Coulombpotential
der Protonen
De Broglie-Wellenlänge von
Streuelektronen
Modell für die Ladungsverteilung im
Kern (Fermi-Verteilung)
234
Gemessene Ladungsdichteverteilung
verschiedener Kerne
[aus Evans: The Atomic Nucleus]
235
Kernspin und Kernmomente
Kerne können ebenfalls einen Spin und ein magnetisches Moment besitzen.
Die magnetischen Momente sind deutlich kleiner als typische atomare Momente.
Bohrsches Magneton
Kernmagneton
Die höheren elektrischen Momente
(z.B. elektrische Qudrupolmomente)
zeugen von deformierten Kernen.
[aus Segre: Nuclei and particles]
236
4.2. Kernkraft und Radioaktivität
4.2.1. Kernkraft
Eigenschaften der Kernkraft:
1.
Sehr starke Kraft (starke Wechselwirkung, ca. 103 mal stärker als die CoulombWechselwirkung zwischen geladenen Teilchen)
2.
Kurze Reichweite, Wirkung nur innerhalb eines Kerns
3.
Unabhängigkeit vom Ladungszustand der Nukleonen; grosse Komplexität
(wesentlich komplexer als die Coulombwechselwirkung)
Wegen der kurzen Reichweite der Kernkräfte ist ein erstes einfaches Modell für das
Kernpotential das Kastenpotential.
V(r)=0 für
r>R
V(r)=-V0 für r<=R
Kastenpotential als Modell für das Kernpotential
237
Aufschlüsse über das Kernpotential erlangt man durch Streuexperimente,
z.B. die Nukleon-Nukleon-Streuung
Klassische Streuung von Teilchen
an einem Potential (z.B. Potentialmulde)
Quantenmechanische Streuung von
Wellenfunktionen an Potentialbarrieren
(z.B. Potentialtopf)
Bemerkung:
• Die Nukleonen testen direkt die Nukleon-Nukleon-Wechselwirkung.
• Als Streuquellen können natürliche radioaktive Isotope oder Neutronen aus
Kernreaktoren benutzt werden.
238
Beispiel für ein Experiment zur Nukleonenstreuung:
Messung der Streuung (Intensität am Detektor) für verschiedene Targets
(hier C-Kerne oder H-Kerne) in Abhängigkeit von der Neutronenenergie
Gemessener Streuquerschnitts σ
Einheit 1 barn (Scheunentor)
= 100 fm2 = 10-28 m2
[aus Enge: introduction to Nuclear Physics]
239
Es ergibt sich folgende Struktur der Kernkraft:
1.
Der Hauptbeitrag ist eine Zentralkraft.
2.
Es gibt eine Spin-abhängige Zentralkraft.
3.
Es existieren nicht-zentrale Kräfte
4.
Die Kernkraft ist (nahezu) lagungsunabhängig.
Heutige Erkenntnis: Die Kraft zwischen den Nukleonen ist eine indirekte Wirkung
(Austauschkraft), die auf der fundamentalen sogenannten starken Kernkraft beruht.
Diese vermittelt auch den Zusammenhalt der Nukleonen, die aus weiteren
(fundamentalen?) Elementarteilchen, den Quarks, zusammengesetzt sind.
Künstlerische Darstellung
der Zusammensetzung
der Nukleonen
[http://www.ep4.rub.de/imperia/md/content/
skripte/ws03-04/mediziener/43_lektion.pdf]
udd Quarks im Neutron
uud Quarks im Proton
240
4.2.2. Radioaktivität
Neben stabilen Kernen existieren radioaktive Kerne, die spontan unter Aussendung
von Teilchen (α-, β-Strahlung) zerfallen. Dabei wandeln sich die Kerne um.
Erste beobachtete Kernumwandlung
(1934 Joliot/Curie):
Dabei ist ΔE = -2.64 MeV!
Q-Wert der Kernreaktion
Der Zerfall erfolgt nicht-deterministisch und folgt dem Gesetz:
somit
radioaktives
Zerfallsgesetz
Wichtige Grössen beim radioaktiven Zerfall:
Zerfallskonstante [1/s]; Einheit Becquerel = 1 Zerfall/s
Mittlere Lebensdauer [s]
Halbwertszeit [s]
241
Zerfallsgesetz und Halbwertszeiten
242
Die Nuklidkarte
Ein geeignetes Ordnungsschema für Nuklide ist die Anordnung in einer Matrix
von Neuronenzahl N (Zeile) und Protonenzahl Z (Spalte).
Eine solche Anordnung heisst Nuklidkarte.
243
Der α-Zerfall
Der α-Zerfall ist die Umwandlung eines Atomkerns in einen anderen Atomkern unter
Emission eines α-Teilchens.
Ein α-Teilchen ist ein Heliumkern.
Es ist also schematisch:
Massenzahl
α-Zerfall
Protonenzahl
Neutronenzahl
Anzahl der Protonen
Beispiel:
238U
Q = 4,25 MeV
234Th
Anzahl der Neutronen
T1/2 = 4,5x109 Jahre
244
Der α-Zerfall kann als quantenmechanisches Tunneln von a-Teilchen durch die
Potentialbarriere des Kernpotential verstanden werden.
E
VCoulomb
r
Tunneleffekt
starke
Kernkraft
0
VKern
α
r
Atomkern
Ladung = +Z e
Vtot
Je grösser die Energie der
α-Teilchen desto kleiner ist
die Halbwertszeit!
Beispiel einiger
α-Zerfälle
245
Der β-Zerfall
Der β-Zerfall ist die Umwandlung eines Atomkerns in einen anderen Atomkern unter
Emission eines β-Teilchens.
Ein β-Teilchen ist ein Elektron e- oder ein Positron e+.
β-Zerfälle
T1/2 = 14,3 Tage
T1/2 = 12,7 Stunden
Anzahl der Protonen
Anzahl der Protonen
Beispiele:
32S
32P
Anzahl der Neutronen
32Cu
32Ni
Anzahl der Neutronen
246
Beim β-Zerfall beobachtet man ein kontinuierliches Energiespektrum:
Energiespektrum der Elektronen aus
dem β-Zerfall von 210Bi
max. kinetische Energie
[aus G. J. Neary, Proc. Phys. Soc. (London), A175, 71 (1940)]
Um beim β-Zerfall Energie- und Impulssatz erhalten zu können (es wurde ein
kontinuierliches Energiespektrum der emittieren Teilchen gefunden!), wurde 1930 von
Wolfgang Pauli das Neutrino ν postuliert.
Es wurde 1953 von F. Reines und C.L. Cowan nachgewiesen.
Das Neutrino wechselwirkt extrem schwach mit Materie.
Eine Hauptquelle für Neutrinos sind leistungsstarke Kernreaktoren oder die Sonne.
(In jeder Sekunde wird man von 4x1011 Neutrinos von der Sonne durchdrungen.)
247
Auch in Supernovae (Explosion von Sternen) werden Neutrino-bursts freigesetzt.
Detektion der Neutrinos der
Supernova 1987a [Kamiokande]
Supernova 1987a
[D.F.Malin, Anglo-Australian
Telescope Board, 1987 ]
Detektion von Neutrinos durch Neutrinoeinfang:
Gemessen wird die Vernichtungsstrahlung des Positrons und die gleichzeitige
charakteristische γ-Strahlung des Cd-Kerns.
248
Ein bedeutender Neutrino-Detektor ist der japanische Superkamiokande Detektor.
Licht der von Neutrinos gestreuten geladenen Teilchen wird in einem mit 50,000 t
Wasser gefüllten Detektor von 11,200 Photodetektoren detektiert.
Blick in das Detektorvolumen
Zerstörte Photomultiplier mach
Kamiokande-Desaster 2001
[Kamioka Observatory, ICRR (Institute for Cosmic Ray
Research), The University of Tokyo]
249
Der γ-Zerfall
Der γ-Zerfall ist der Übergang zwischen verschiedenen quantenmechanischen Zuständen
im Atomkern.
Es werden keine Teilchen, sondern hochenergetische elektromagnetische Strahlung
(γ-Strahlung) emittiert.
Die Zustände eines Kerns können z.B. im Schalenmodell beschrieben werden.
Schema möglicher
Energiezustände
im Atomkern
Experimentelle Anordnung
zur γ-Spektroskopie
Die Lebensdauern liegen zwischen 10-8 bis 10-15 s.
Energie der emittierten γ-Strahlung:
Energiedifferenz
zweier Zustände
kinetische Energie
d. Rückstoss
250
Gemessenes γ-Spektrum
[aus: J. Gerl et al., Phys. Lett.120B, 83 (1983)]
251
Klassifizierung von radioaktiver Strahlung
252
4.2.3. Anwendung: Radiometrische Zeitmessung
Die Halbwertszeit radioaktiver Nuklide kann als natürliche Uhr zur Bestimmung des Alters
von verschiedenen Proben benutzt werden.
Prinzip: Messung des Verhältnisses von radioaktivem Nuklid zu seinem Zerfallsprodukt
Verwendet werden natürlich vorkommende radioaktive Nuklide. Das sind:
• Nuklide, die eine sehr lange Lebensdauer haben und deshalb noch heute strahlen.
• Nuklide, die durch hochenergetische Prozesse, z.B. durch kosmische Strahlung
ständig neu erzeigt werden.
Beispiel 1:
T1/2 = 1,25x109 Jahre
Verhältnis von 40K zu 40Ar bestimmt das Alter von Gesteinsproben.
Beispiel 2:
Reaktion durch kosmische Strahlung i.d. Atmosphäre
T1/2 = 5730 Jahre
253
Bei der 14C-Methode nutzt man aus, dass lebende Organismen ständig Kohlenstoff
in Form von CO2 mit der Umgebung austauschen.
Das Verhältnis von 12C/14C bleibt konstant bis der Organismus stirbt. Danach nimmt
die Konzentration von 14C ab.
Bereich der Alterbestimmung
1000-30000 Jahre
Datierung des Turiner Grabtuches
(rechts) mit der RadiocarbonUntersuchung auf 1290-1360
254
4.3. Kernmodelle
Atomkerne sind komplexere Gebilde als Atome. Die theoretische Beschreibung von Kernen
basiert daher auf verschiedenen Kernmodellen.
4.3.1. Das Tröpfchenmodell
Manche Eigenschaften von Kernen ähneln denen von makroskopischer kondensierter
Materie.
C.F. von Weizsäcker entwickelte 1935 das Tröpfchenmodell.
Nach diesem Modell tragen 5 Terme zur Bindungsenergie B in Atomkernen bei:
1.
Volumenenergie
Kondensationsenergie beim Vereinigen der Kerne
2.
Oberflächenenergie
Nukleonen an Oberfläche sind schwächer gebunden
3.
Coulombenergie
Coulombabstossung der Protonen
255
4.
Asymmetrieenergie
Die Bindungsenergie wird verringert, wenn Z ungleich N
5.
gg-Kern
Paarungsenergie
ug, gu-Kern
uu-Kern
Kerne mit Paaren von Neutronen und Protonen sind stabiler!
Mit allen Beiträgen ergibt sich die von Weizsäckersche Massenformel:
Die obere Zeile zählt die Massen von Protonen und Neutronen,
die untere Zeile ist der Massendefekt aufgrund der Bindungsenergie.
256
Mit der Massenformel lassen sich Abschätzungen über die Stabilität von Kernen geben.
Stabilität in einer Isobarenreihe (A=konstant)
Für isobare Kerne hat die Massenformel die Form:
Parabel mit Koeffizienten c1 und c2
Stabilität von isobaren
Kernen (A=ungerade)
Stabilität von isobaren Kernen unter
Berücksichtigung der Paarungsenergie:
Stabilität mehrerer gg-Kerne;
Instabilität der uu-Kerne
257
Protonenzahl des stabilsten Kerns in einer Isobarenreihe
Die Stabilitätsbedingung in einer Isobarenreihe ist:
Dies führt mit zunehmender Massenzahl zu einer Bevorzugung einer
grösseren Neutronenzahl.
Weitere Voraussagen der Massenformel sind über die Bedingung für den α-Zerfall und die
spontane symmetrische Kernspaltung möglich.
Lehrbücher der Kernphysik
258
4.3.2. Das Schalenmodell
Das Schalenmodell geht von einem kastenförmigen Kernpotential aus, das ähnlich wie
beim Coulombpotential der Atome sukzessive mit Nukleonen gefüllt wird.
Kastenpotential im
Schalenmodell.
Wegen der Coulombabstossung sind die
Protonen schwächer
gebunden.
In diesem Modell können insbesondere die γ-Spektren als Zerfälle von angeregten
Kernzuständen erklärt werden.
Ähnlich wie bei Edelgasen erweisen sich Kerne mit abgeschlossenen Schalen als
besonders stabil.
259
Die Nukleonenzahlen für abgeschlossene Schalen (jeweils für Protonen oder Neutronen)
heissen magische Zahlen.
magische Zahlen: 2, 8, 20, 28, 50, 82, 126, ...
Kerne mit magischen Zahlen sowohl für Neutronen (N) als auch fürProtonen (Z) heissen
doppelt magisch.
Beispiele:
18O(Z=8)
40Ca(Z=20,N=20)
208Pb(Z=82,N=126)
Ein besonders stabiler doppelt magischer Kern ist das α-Teilchen: 4He(Z=2,N=2)
16O
im Schalenmodell
260
4.4. Kernreaktionen
4.4.1. Allgemeines zu Kernreaktionen
Die heute noch vorkommenden radioaktiven Isotope sind die langlebigsten der bei der
Synthese der Elemente (vor 15x109 Jahren) erzeugten Isotope.
α-Zerfallsreihen
Weitere natürliche radioaktive Isotope sind:
β-Zerfall: 40K, 87Rb, 187Re, 14C, 90Sr, 137Cs
Die Isotope zerfallen über z.T. verzweigte Kaskaden von Zerfällen
(α-, β-, γ-Zerfälle, Spaltung, ...) bis hin zu einem stabilen Kern.
261
Beispiel: Zerfallsreihe von 238U
262
Beispiel: Zerfallsreihe von 232Th
263
4.4.2. Kernspaltung
Kernreaktionen können auch künstlich durch Beschuss von Kernen mit (hochenergetischen)
Teilchen ausgelöst werden.
Eine solche Reaktion beschreibt man typischerweise:
Target
Projektil
Endkern
Ejektil
Abkürzende Schreibweise:
Eine besonders überraschende Reaktion wurde in den späten 1930ern von
O. Hahn, F. Strassmann und L. Meitner beobachtet.
Befund:
Der Beschuss von Uransalzen
mit thermischen Neutronen liefert
Spaltprodukte mit überraschend
kleiner Massenzahl!
O. Hahn
L. Meitner
264
Massenverteilung der Spaltprodukte
nach Beschuss von 235U mit thermischen
Neutronen
[aus Tipler Physik]
1939 konnte L. Meitner zusammen
mit O. Frisch die korrekte Deutung
des Prozesses als Kernspaltung
(s. rechts) geben.
265
Der Prozess ist der folgende:
Absorption eines Neutron durch 235U
Spaltung des hochangeregten 236U unter Emission von 2 Neutronen
1.
2.
Spaltung von 235U
Zerfall der Spaltprodukte 140Xe und 94Sr.
3.
weitere Zerfallsreihen
Freiwerdene Energie pro Spaltvorgang (Massendefekt):
Bohr und Wheeler konnten die Kernspaltung im Tröpfchenmodell beschreiben.
t
Deformation, Abschnürung
und Spaltung eines Kerns
266
Die potentielle Energie beim Spaltungsprozess weist ähnlich wie beim α-Zerfall
eine Barriere auf, durch die bei Energieanhebung (Absorption eines Neutrons)
getunnelt werden kann.
Potentielle Energie des Kerns in
Abhängigkeit der Kerndeformation
Kernmasse als Funktion der
Massenzahl
Schwere Kerne haben die Tendenz
zur Spaltung, leichte Kerne haben
die Tendenz zur Fusion.
267
Bei jedem Spaltprozess werden mehrere Neutronen frei.
Kettenreaktion
268
4.4.3. Kernenergie
Kernreaktionen können zur Energiegewinnung genutzt werden, wenn leichte Kerne
verschmelzen (Fusion) oder schwere Kerne sich spalten (fission).
Energiegewinn bei elektronischen Prozessen (Verbrennung):
einige eV
Energiegewinn bei Kernumwandlung (Fusion, Fission):
einige MeV
Kernfusion
Kernspaltung
269
Kontrollierte Kernspaltung
Für die Aufrechterhaltung einer kontrollierten Kettenreaktion in einem Kernkraftwerk
sind drei Probleme zu lösen:
1.
Neutronenverlust Neutronen können den Reaktor verlassen, bevor sie erneut
eingefangen werden. Eine kugel- (oder würfel-)förmige Anordnung des Reaktorkerns minimiert den Verlust (Verhältnis Oberfäche/Volumen).
2.
Energiereiche Neutronen Die erzeugten Neutronen haben mit im Mittel 2 MeV eine
zu grosse Energie für den erneuten Einfang (thermisch = 0.04 eV). Ein Moderator
(z.B Wasser) reduziert die Energie der Neutronen durch Stösse.
3.
Neutroneneinfang In einem Energiebereich von 1-100 eV werden Neutronen von
effektiv eingefangen (ohne dies zu spalten). Sie stehen dann nicht mehr für
die Spaltung von 235U zur Verfügung. Eine separierte räumliche Anordnung von
Brennstäben und Moderatorvolumina minimiert dieses Problem.
238U
Die Kettenreaktion ist kontrolliert, wenn der Multiplikationsfaktor = 1 ist
Multiplikationsfaktor = (anfängl. Anzahl der Neutronen)/(Anzahl der Neutronen nach einem Zyklus)
270
Multiplikationsfaktor = 1
Multiplikationsfaktor > 1
Multiplikationsfaktor < 1
kritisch
überkritisch
unterkritisch
Der Multiplikationsfaktor kann durch
Kontrollstäbe, die Neutronen einfangen,
(z.B. Cd) eingestellt werden.
Neutronenbilanz in einem Reaktor
Neutronenbilanz in einem
Kernreaktor
[aus: Halliday Physik]
Prinzipieller Aufbau eines Kernkraftwerks
271
272
Kernfusion
Die natürliche Kernfusion (Verschmelzung von Wassertoff zu Helium) ist der
Energielieferant für die Sonne (Leistung 4x1026 W).
Unter extrem hohen Druck läuft folgender Prozess ab:
Kernfusionsprozess in der Sonne
(stark vereinfacht)
Energiegewinn ΔQ= 26,7 MeV
Ist der Brennstoff Wasserstoff verbraucht so laufen weitere Kernfusionsreaktionen ab,
die immer schwerere Kerne als Endprodukt haben (z.B. He
C).
Elementsynthese in der Sonne.
273
Die kontrollierte Kernfusion unter terrestrischen Bedingungen ist ein Ziel der Fusionsforschung.
Folgende Reaktionen sollen i. e. magnetisch im Vakuum eingeschlossenen Plasma ablaufen:
Drei Bedingungen sind zu realisieren:
1.
2.
3.
Hohe Teilchendichte n
Hohe Plasmatemperatur T
Lange Einschlusszeit τ
Im rentablen Betrieb eines thermonuklearen Reaktors muss das
Lawson-Kriterium gelten:
rechts: geplanter Fusionsreaktor
Wendelstein des MPI Greifswald
274
Schematischer Aufbau eines Tokamak-Fusionsreaktors
[aus: Tipler Physik]
275
Unkontrollierte Kernspaltung
Das Potential der nuklearen Kettenreaktion als Waffe mit millionenfach erhöhter Sprengkraft
(Megatonnen TNT Äquivalent) wurde rasch erkannt.
Im Manhattan Projekt wurde ab 1942 die Entwicklung einer Atombombe unter der
wissenschaftlichen Leitung von R. Oppenheimer betrieben.
[s.auch R. Rhodes, The making of the atomic bomb]
Der erste Test erfolgte 1945 (trinity) ebenso der erste Einsatz (little boy, fat man)
1952 folgt die erste Wasserstoffbombe.
J. R. Oppenheimer
Wasserstoffbombe
(Eniwetok Atoll, 1952)
276