Theoretische Mechanik - Universität Paderborn

Skript zur Vorlesung
Theoretische Mechanik
Prof. Dr. habil. Wolf Gero Schmidt
8. Mai 2015
Universität Paderborn, Lehrstuhl für Theoretische Physik
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Inhaltsverzeichnis
1 Kinematik eines Massenpunkts
5
1.1
Bahnkurve, Geschwindigkeit und Beschleunigung . . . . . . . . . . . . . .
1.2
Krummlinige Koordinatensysteme . . . . . . . . . . . . . . . . . . . . . . . 10
1.3
Grundtypen der Bewegung . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.4
Harmonischer Oszillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2 Newtonsche Mechanik
2.1
2.2
2.3
5
33
Die Newtonschen Axiome . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.1.1
Das Trägheitsgesetz . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.1.2
Das Grundgesetz der Dynamik . . . . . . . . . . . . . . . . . . . . 34
2.1.3
Das Wechselwirkungsgesetz . . . . . . . . . . . . . . . . . . . . . . 37
2.1.4
Superposition von Kräften . . . . . . . . . . . . . . . . . . . . . . . 37
2.1.5
Bewegte Bezugssysteme . . . . . . . . . . . . . . . . . . . . . . . . 37
Dynamik eines Massenpunktes
. . . . . . . . . . . . . . . . . . . . . . . . 44
2.2.1
Bewegungsgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . 44
2.2.2
Impulsbilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.2.3
Energiebilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.2.4
Drehimpulsbilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
2.2.5
Erhaltungssätze und Integration der Bewegungsgleichungen . . . . 57
2.2.6
Spezielle Probleme . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
Dynamik eines MP-Systems . . . . . . . . . . . . . . . . . . . . . . . . . . 79
2.3.1
Bewegungsgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . 79
2.3.2
Impulsbilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
2.3.3
Energiebilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
2.3.4
Virialsatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
2.3.5
Drehimpulsbilanz . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.3.6
Spezielle Probleme . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
3 Lagrangesche Mechanik
3.1
3.2
98
Das d’Alembertsche Prinzip . . . . . . . . . . . . . . . . . . . . . . . . . . 98
3.1.1
Bedingungsgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . 98
3.1.2
Das d’Alembertsche Prinzip . . . . . . . . . . . . . . . . . . . . . . 101
3.1.3
Bilanzgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
3.1.4
Spezielle Probleme . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
3.1.5
Starrer Körper . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
Lagrangesche Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
3.2.1
Lagrangesche Gleichungen 1. Art . . . . . . . . . . . . . . . . . . . 124
3.2.2
Lagrangesche Gleichungen 2. Art . . . . . . . . . . . . . . . . . . . 130
3.2.3
Erhaltungssätze und Symmetrien . . . . . . . . . . . . . . . . . . . 139
4 Hamiltonsche Mechanik
145
4.1
Prinzip der kleinsten Wirkung . . . . . . . . . . . . . . . . . . . . . . . . . 145
4.2
Hamiltonsche Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
4.3
Poisson-Klammern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
5 Spezielle Relativitätstheorie
5.1
5.2
5.3
158
Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
5.1.1
Michelson-Experiment - Lorentzkontraktion . . . . . . . . . . . . . 158
5.1.2
Zeitdilatation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
5.1.3
Lorentz-Transformation . . . . . . . . . . . . . . . . . . . . . . . . 170
Raum-Zeit-Mannigfaltigkeit . . . . . . . . . . . . . . . . . . . . . . . . . . 176
5.2.1
Meßvorschriften und Gleichzeitigkeit . . . . . . . . . . . . . . . . . 176
5.2.2
Kausalität von Ereignissen . . . . . . . . . . . . . . . . . . . . . . . 183
Relativistische Mechanik . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
5.3.1
Masse und Energie . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
3
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
5.3.2
Geschwindigkeitsabhängigkeit der trägen Masse . . . . . . . . . . . 188
4
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
1 Kinematik eines Massenpunkts
1.1 Bahnkurve, Geschwindigkeit und Beschleunigung
Kinematik ≡ geometrische Bewegungslehre, interessieren uns zunächst nicht für Ursachen
der Bewegung
Im kinematischen Sinne ist die Bewegung eines Körpers bestimmt, wenn die Lage des
Körpers relativ zu einem anderen Körper zu jedem Zeitpunkt angebbar ist.
Wir idealisieren einen Körper zunächst durch einen Massenpunkt.
Wir wählen in dem Bezugskörper (z.B. Erde) einen Ausgangspunkt O (Koordinatenursprung), durch den die Achsen eines rechtwinkligen Koordinatensystems verlaufen.
~ ≡ ~r charakterisiert.
⇒ Die Lage des Massenpunktes P ist durch den Ortsvektor OP
Die Bewegung des Massenpunktes ist bekannt, wenn der Ortsvektor ~r als Funktion der
Zeit bekannt ist:
~r = ~r(t)
5
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Speziell in kartesischen Koordinaten:
~r(t) = x(t)e~x + y(t)e~y + z(t)e~z
Die Funktionen x(t), y(t) und z(t) seien eindeutig und mindestens zweimal differenzierbar.
Die Raumkurve ~r(t) ist die Bahnkurve des Massenpunkts.
Zum Zeitpunkt t ist der Massenpunkt bei ~r(t), nach der Zeitspanne ∆t bei ~r(t + ∆t) =
~r + ∆~r.
Die auf die Zeiteinheit bezogene mittlere Verrückung ist durch den Vektor
~r(t + ∆t) − ~r(t)
∆~r
=
∆t
∆t
gegeben, der von der Zeit t und der Zeitspanne ∆t abhängt.
Den von ∆t unabhängigen Vektor der Geschwindigkeit ~v (t) findet man als Grenzwert
~v (t) ≡ ~r˙ (t) ≡
d~r
~r(t + ∆t) − ~r(t)
= lim
∆t→0
dt
∆t
6
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Speziell in kartesischen Koordinaten gilt
~r˙ = ẋe~x + ẏ e~y + ż e~z
Geometrisch ergibt sich der Vektor der Geschwindigkeit als Grenzlage der Sekante durch
die Vektoren ~r(t + ∆t) und ~r(t) pro Zeitintervall ∆t in der Grenze ∆t → 0, d.h. die
Richtung der Geschwindigkeit zur Zeit t ist durch die Richtung der Tangente im Punkt
P der Bahnkurve ~r(t) gegeben.
~v = v T~
mit T~ . . . Tangenteneinheitsvektor
und v = |~v |
Beweis:
Definieren Bogenlänge der Bahnkurve zwischen P und dem zur geeignet gewählten Anfangszeit t0 zugehörigen P0 durch
Zt
s = s(t) =
Zt
|d~r|
ds =
t0
7
t0
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wegen ~r = ~r [s(t)] gilt
~v =
d~r
d~r ds
·
=
dt
ds |{z}
dt
|{z}
v
T~
~v (t) wird als Hodograph bezeichnet.
Die Beschleunigung ~a(t) ist definiert als zeitliche Änderung des Geschwindigkeitsvektors:
d~v
d2~r
≡ 2
dt
dt
~a(t) ≡ ~v˙ (t) ≡ ~r¨(t) ≡
k
~
v (t+∆t)−~
v (t)
∆t
∆t→0
lim
Speziell in kartesischen Koordinaten
~r¨ = ẍe~x + ÿ e~y + z̈ e~z
d~v
d ~
˙
~a =
=
v T = v̇ T~ + v T~
dt
dt
dT~
dT~ ds
dT~
˙
gilt T~ =
=
·
=v
dt
ds |{z}
dt
ds
v
d ~ ~
T~ · T~ = 1 ⇒
T ·T =0
ds
k
2 · T~ ·
⇒
dT~ ~
⊥T
ds
8
~
dT
ds
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir definieren den Hauptnormaleneinheitsvektor
~ dT~ d
T
dT~
~ =
N
/ = R
ds ds ds
wobei wir den lokalen Krümmungsradius R eingeführt haben. Der Krümmungsradius
R ist der Radius des Kreises, der die Bahnkurve am betrachteten Punkt am besten
approximiert, siehe Abbildung unten:
Für ∆t → 0 gilt offensichtlich:
ds ~ dϕ =
= dT R
dT~ 1
⇒ =
ds R
⇒R=|
dT~ −1
|
ds
~
Mit R = | ddsT |−1 erhalten wir für die Beschleunigung
~a =
d~v
dT~
= v̇ T~ + v 2
dt
ds
=
v̇ T~
|{z}
Anteil an Beschleunigung
infolge Betragsänderung der
Geschwindigkeit
v2 ~
N
|R{z }
+
infolge Richtungsänderung der
Geschwindigkeit
9
~
mit T~ ⊥N
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
1.2 Krummlinige Koordinatensysteme
In kartesischen Koordinaten sind die Koordinatenlinien Geraden. Oft sind aber auch
krummlinige Koordinaten zielführend. Dann ändern die Koordinatenlinien ihre Richtung,
so daß die Einheitsvektoren ortsabhängig werden. Stehen die Koordinatenlinien senkrecht
aufeinander spricht man von rechtwinkligen (krummlinigen) Koordinaten. Beispiel sind
Zylinder- und Kugelkoordinaten. Der allgemeinste Fall sind schiefwinklige krummlinige
Koordinaten. Dafür lassen sich zwei Arten von Koordinaten und Basisvektoren definieren.
Wir betrachten schiefwinklige Koordinaten
xi = xi (x, y, z)
i = 1, 2, 3
mit den Umkehrtransformationen
x = x x1 , x2 , x3
y = y x1 , x2 , x3
z = z x1 , x2 , x3
Wir definieren kovariante Basisvektoren
∂~r
g~i :=
=
∂xi
∂x ∂y ∂z
,
,
∂xi ∂xi ∂xi
∂xi ∂xi ∂xi
,
,
∂x ∂y ∂z
und kontravariante Basisvektoren
~ i=
g~i := ∇x
10
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Für rechtwinklige Koordinatensysteme gilt:
g~i k~
gi
(Begründung später: weil dann der metrische Fundamentaltensor diagonal ist)
Die Skalarprodukte
gik = g~i · g~k = gki
g ik = g~i · g~k = g ki
hängen von den gewählten Koordinaten ab, da die Basisvektoren von ihnen abhängen.
Invariant sind hingegen Skalarprodukte von kovarianten und kontravarianten Basisvektoren
∂~r ~ k
∂xk
gik = g~i · g~k =
·
∇x
=
= δik
∂xi
∂xi



1 k = i
k
mit dem Kroneckersymbol δi =


0 k 6= i
Kovariante und kontravariante Basisvektoren bilden jeweils eine Entwicklungsbasis für
einen beliebigen Vektor ~q:
~q = q k g~k = qk g~k
(Hier gilt die Einstein’sche Summenkonvention: über zwei gleiche ko- und kontravariante
Indizes ist zu summieren)
Bestimmung der Koeffizienten q k bzw. qk ?
~q = q k g~k | · g~i
⇒ q i = g~i · ~q
11
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
analog:
~q = qk g~k | · g~i
⇒ qi = g~i · ~q
Ko- und kontravariante Komponenten lassen sich einfach ineinander umrechnen:
q i = g~i · ~q = g ik qk
k
g~k qk
analog: qi = gik q k
Skalarprodukt zweier Vektoren ~q und p~?
~q · p~ = qi pk g~i g~k = qi pi
|{z}
δki
k
= q i pi
gik q k pi
k
g ik qk pi
Die Größe gik heißt metrischer Fundamentaltensor, er bestimmt die Länge des Bogenelements in dem jeweils gewählten Koordinatensystem. Aus der Definition g~i :=
∂~
r
∂xi
folgt
mittels Kettenregel unmittelbar die
Metrische Fundamentalgleichung
d~r = g~i dxi = g~i dxi
deren rechte Seite die dxi einführt. Für das Quadrat des Differentials der Bogenlänge
ergibt sich
ds2 = d~r · d~r = gik dxi dxk = g ik dxi dxk
12
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Bemerkung:
In der "flachen"Raum-Zeit des Minkowski-Raumes mit
⇒
Vierervektoren x = (x0 , ~r) = (ct, x, y, z) gilt für das unter Lorentztransformationen
invariante Abstandsquadrate zweier Erreignisse
ds2 = (dx0 = cdt)2 − (dx1 = dx)2 − (dx2 = dy)2 − (dx3 = dz)2 ,
entsprechend folgt
g00 = 1, g11 = g22 = g33 = −1, gij = 0 i 6= j.
Anwendungen bei Integration und Differentiation:
Als Volumenelement (im dreidimensionalen Raum) kann das von den Vektoren
dr~1 = g~1 dx1
dr~2 = g~2 dx2
dr~3 = g~3 dx3
aufgespannte Spatprodukt angesehen werden, d.h.
1
2
3
dV = |g~1 · (g~2 × g~3 )| dx dx dx =
∂(x, y, z) 1
2
3
∂ (x1 , x2 , x3 ) dx dx dx
|
{z
}
Betrag der Funktionaldeterminante
Entsprechend können die Flächen des vektoriellen Flächenelements angegeben werden
dA~1 = g~2 × g~3 dx2 dx3 usw.
Wir können auch Differentialoperatoren in beliebigen Koordinaten angeben.
13
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
~ einer Funktion f , nach Definition gilt:
Beispiel: Gradient ∇
~
df = d~r · ∇f
k
∂f
dxi
i
∂x
k
g~i dxi
~ = ∂f dxi
⇒ g~i dxi · ∇f
∂xi
~ = ∂f |g~i
g~i · ∇f
∂xi
∗ ~i ∂f
~k = δ k
~ =
∇f
g
∗
:
g
~
·
g
i
i
∂xi
∂f
∗∗
= g~i g ik k
∗∗ : q i = g ik qk
∂x
Anwendung in Mechanik:
Geschwindigkeit und Beschleunigung eines Massenpunkts in beliebigen Koordinaten.
Wir starten mit der metrischen Fundamentalgleichung
d~r = g~i dxi
⇒
d~r
dxi
= ~r˙ = g~i
dt
dt
Geschwindigkeit ~r˙ = ẋi g~i
d
dt |
→
Beschleunigung ~r¨ = ẍi g~i + ẋi g~˙i
Speziell in rechtwinkligen Koordinaten ist der metrische Fundamentaltensor diagonal
gik = λ2i δik (keine Summenkonvention)
14
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
→ Basisvektoren g~i und g~i sind parallel
g~i = λ2i g~i kg~i (keine Summenkonvention)
Die orthogonalen Einheitsvektoren erhalten wir aus
e~i =
g~i
= λi g~i
λi
damit Geschwindigkeit
~r˙ =
3
X
ẋi λi e~i
i=1
und Beschleunigung
~r¨ =
3 n
o
X
ẍi λi e~i + ẋi λ̇i e~i + ẋi λi e~˙i
i=1
Berechnung von e~˙i aus der Definition
e~i =
g~i
1 ∂~r
=
(keine Summenkonvention)
λi
λi ∂xi
Beispiel: Zylinderkoordinaten
x1 = ρ
x2 = ϕ
x3 = z
15
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
bzw. ρ =
Umrechnung x = x (ρ, ϕ) = ρ cos ϕ
p
x2 + y 2
y = y (ρ, ϕ) = ρ sin ϕ
ϕ = arctan
z=z
z=z
y
x
∂~r
= (cos ϕ, sin ϕ, 0)
∂ρ
∂~r
g~2 =
= (−ρ sin ϕ, ρ cos ϕ, 0)
∂ϕ
∂~r
g~3 =
= (0, 0, 1)
∂z
⇒ g~1 =
x
p
~ =∇
~ x2 + y 2 =
g~1 = ∇ρ
y
!
p
,p
, 0 = (cos ϕ, sin ϕ, 0)
x2 + y 2
x2 + y 2
y
y
x
sin
ϕ
cos
ϕ
~
2
~ =∇
~ arctan = −
g = ∇ϕ
,
,0 = −
,
,0
x
x2 + y 2 x2 + y 2
ρ
ρ
~ = (0, 0, 1)
g~3 = ∇z
Der metrische Fundamentaltensor
gik


1 0 0



2
= g~i · g~k = 
0 ρ 0


0 0 1
ist, wie für rechtwinklige Koordinaten erwartet, diagonal.
λρ = 1
gik = λ2i δik
λϕ = ρ
λz = 1
Jetzt berechnen wir die orthogonalen Einheitsvektoren.
16
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
e~i =
g~i
λi
e~ρ = (cos ϕ, sin ϕ, 0)
⇒
e~ϕ = (− sin ϕ, cos ϕ, 0)
e~z = (0, 0, 1)
Wir können jetzt den Gradienten in Zylinderkoordinaten ausdrücken:


∂f
∂f
1
cos
ϕ
−
sin
ϕ
∂ρ
ρ
∂ϕ 



∂f
~
∂f
∂f 
~ = gi
∇f
=
sin ϕ ∂ρ + ρ1 cos ϕ ∂ϕ


i
∂x


∂f
∂z
Diese Gleichung ist noch in kartesischen Komponenten ausgedrückt, zu „echter“ Zylinderkoordinatendarstellung kommen wir durch Projektion auf e~ρ , e~ϕ und e~z .
~ · e~ρ = ∂f
∇f
∂ρ
1
~ · e~ϕ = ∂f
∇f
ρ ∂ϕ
~ · e~z = ∂f
∇f
∂z
1 ∂f
∂f
∂f
e~ρ +
e~ϕ +
e~z
⇒ gradf =
∂ρ
ρ ∂ϕ
∂z
Volumenelement in Zylinderkoordinaten
dV = |g~1 · (g~2 × g~3 )| dx1 dx2 dx3 = ρdρdϕdz
k
|
{z
}
dxdydz
ρ
Geschwindigkeit in Zylinderkoordinaten
~r˙ =
3
X
ẋi λi e~i = ρ̇e~ρ + ϕ̇ρe~ϕ + ż e~z
i=1
17
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beschleunigung in Zylinderkoordinaten
~r¨ =
3 n
o
X
ẍi λi e~i + ẋi λ̇i e~i + ẋi λi e~˙i = ρ̈e~ρ + ρ̇e~˙ρ + ϕ̈ρe~ϕ + ϕ̇ρ̇e~ϕ + ϕ̇ρe~˙ϕ + z̈ e~z + ż e~˙z
i=1
Wie sehen e~˙ρ , e~˙ϕ und e~˙z aus?
e~ρ = cos ϕe~x + sin ϕe~y
e~˙ρ = −ϕ̇ sin ϕe~x + ϕ̇ cos ϕe~y = ϕ̇e~ϕ
e~ϕ = − sin ϕe~x + cos ϕe~y
e~˙ϕ = −ϕ̇ cos ϕe~x − ϕ̇ sin ϕe~y = −ϕ̇e~ρ
e~z = e~z ⇒ e~˙z = 0
Damit
~r¨ = e~ρ ρ̈ − ρϕ̇2 + e~ϕ (ρϕ̈ + 2ρ̇ϕ̇) + z̈ e~z
Beispiel: Kugelkoordinaten
x = r sin θ cos ϕ
y = r sin θ sin ϕ
z = r cos θ
18
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Offensichtlich (Beweis Übung) gilt:
gik


1
0
0




2
=
0 
0 r



0 0 r2 sin2 θ
e~r = (sin θ cos ϕ, sin θ sin ϕ, cos θ)
e~θ = (cos θ cos ϕ, cos θ sin ϕ, − sin θ)
e~ϕ = (− sin ϕ, cos ϕ, 0)
~r˙ = ṙe~r + θ̇re~θ + ϕ̇r sin θe~ϕ
1 d 2
2
2
2
2
¨
θ̇r − ϕ̇ r sin θ cos θ e~θ
~r = r̈ − θ̇ r − ϕ̇ r sin θ e~r +
r dt
1 d
ϕ̇r2 sin2 θ e~ϕ
+
r sin θ dt
1.3 Grundtypen der Bewegung
Die einfachste Bewegung eines Massenpunktes ist die geradlinige gleichförmige Bewegung, für die
~r˙ = ~v = const.
gilt.
⇒ ~r¨ = 0
19
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Bahnkurve folgt offensichtlich einer Geraden, deren Richtung durch ~v bestimmt wird:
~r(t) = ~v (t − t0 ) + r~0
Die gleichförmig beschleunigte Bewegung ist durch
~r¨ = ~a = const.
definiert.
⇒ ~v = ~r˙ = ~at + ~b
Bahnkurve:
1
~r(t) = ~at2 + ~bt + ~c
2
mit beliebigen Vektoren ~b und ~c. Für die Anfangsbedingungen
t = t0
~r(t0 ) = r~0
~r˙ (t0 ) = v~0
gilt offensichtlich
~r˙ (t0 ) = v~0 = ~at0 + ~b ⇒ ~b = v~0 − ~at0
1
~r(t0 ) = r~0 = ~at20 + ~bt0 + ~c
k
2
v~0 − ~at0
1
⇒ ~c = r~0 + ~at20 − v~0 t0
2
20
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit ergibt sich für die Bahnkurve:
1
1
1
~r(t) = ~at2 + v~0 t − ~at0 t + r~0 + ~at20 − v~0 t0 = (t − t0 )2~a + (t − t0 )v~0 + r~0
2
2
2
D.h. die Bahnkurve liegt in einer durch ~a und v~0 aufgespannten Ebene, die gleichförmig
beschleunigte Bewegung ist somit eine ebene Bewegung:
Die Bewegung setzt sich zusammen aus einer geradlinig gleichförmigen Bewegung und
einer geradlinig gleichförmig beschleunigten Bewegung. Ohne Verlust an Allgemeinheit
liegen ~a und v~o in der x-y-Ebene, es gelte
~a = ae~y
v~0 = v0x e~x + v0y e~y
dann gilt x − x0 = v0x (t − t0 )
1
y − y0 = a(t − t0 )2 + v0y (t − t0 )
2
21
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Durch Eliminierung der Zeit erhält man die Bahngleichung:
y − y0 =
v0y
1 a
(x − x0 )
(x − x0 )2 +
2
2 v0x
v0x
⇒ Parabel, deren Achse parallel zur Beschleunigungsrichtung (d.h. e~y ) ist.
Falls v~0 parallel zu ~a ist oder v~0 = 0, entartet die Bewegung in eine geradlinige Bewegung.
Beispiel: Wurf im Schwerefeld
Die y-Achse zeige nach oben, d.h. ~a = −g e~y
v0x = v0 cos α
v0y = v0 sin α
Für x0 = y0 = 0 = t0 gilt dann:
x = v0 t · cos α
1
y = v0 t · sin α − gt2
2
• Wurfparabel ergibt sich zu
y = x tan α −
22
g
x
2v02 cos2 α
2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
• Steigzeit ergibt sich aus
!
ẏ = 0 ⇒ v0 sin α − gts = 0
ts =
v0 sin α
g
• Wurfdauer
1
!
y = 0 ⇒ v0 td sin α − gt2d = 0
2
2v0 sin α
td =
= 2ts
g
!
(y = −h falls der Wurf aus der Höhe h erfolgt)
• Wurfhöhe
y(ts ) =
1 v02 sin2 α
v02 sin2 α 1 v02 sin2 α
− g
=
g
2
g2
2
g
• Wurfweite
x(td ) = v0 cos α
2v0 sin α ∗ v02 sin(2α)
=
g
g
(∗ : sin(2α) = 2 sin α cos α)
⇒ maximale Wurfweite für α = 45◦ , kleinere Weiten können im Steilwurf und im
Flachwurf erzielt werden.
23
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Ein Massenpunkt führt eine gleichförmige Kreisbewegung aus, wenn er sich mit konstanter Bahngeschwindigkeit v = |~v | = const. auf einem Kreis mit festem Radius R = const.
bewegt.
Beschreibung mit ebenen Polarkoordinaten
x = ρ cos ϕ
y = ρ sin ϕ
vgl. Zylinderkoordinaten (1.2)
~r˙ = ρ̇e~ρ + ϕ̇ρ e~ϕ
|{z}
q
vρ = 0 vϕ = ωR = v = const.
wobei ω = ϕ̇ die Winkelgeschwindigkeit bezeichnet.
ϕ̇ = ω =
v
= const. ⇒ ϕ(t) = ω(t − to ) + ϕ0
R
früher (1.2) ~r¨ = ρ̈ − ρϕ̇2 e~ρ + (ρϕ̈ + 2ρ̇ϕ̇) e~ϕ
d.h. aρ = ρ̈ − ϕ̇2 ρ = −ω 2 R = −
aϕ = ρϕ̈ + 2ϕ̇ρ̇ = 0
k
k
0
0
24
v2
R
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
⇒ Beschleunigung zeigt zum Mittelpunkt des Kreises (Radialbeschleunigung) und hat
den Betrag ω 2 R
~a = −ω 2 Re~ρ = −
v2
e~ρ
R
betrachten Zeitabhängigkeit
ϕ = ω(t − t0 ) + ϕ0
!
∆ϕ = ω∆t = 2π
Mit ∆t = T (Umlaufzeit) ergibt sich:
ω=
mit Frequenz ν =
2π
= 2πν
T
1
T
Die Winkelgeschwindigkeit ω wird auch als Kreisfrequenz bezeichnet.
In kartesischen Koordinaten gilt:
x = ρ cos ϕ ⇒ x(t) = R cos (ωt + α)
π
y = ρ sin ϕ ⇒ x(t) = R sin (ωt + α) = R cos ωt + α −
2
(mit α = ϕ0 − ωt0 )
Die Projektionen der Kreisbewegung auf die x- und y-Achse sind harmonische Schwingungen.
Genauer: Die gleichförmige Kreisbewegung kann als Überlagerung zweier zueinander
senkrecht stehender harmonischer Schwingungen angesehen werden, deren Phasendifferenz
π
2
ist.
25
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
1.4 Harmonischer Oszillator
Wir betrachten eine periodische, lineare Bewegung eines Massenpunktes längs der xAchse um den Ursprung.
x(t + T ) = x(t)
mit Periodendauer T .
Die periodische Bewegung ist eine harmonische Schwingung, wenn die Auslenkung aus
dem Ursprung eine Kosinus- oder Sinusfunktion der Zeit ist.
x(t) = A cos(ωt + α)
A. . . Amplitude, α. . . Phase, Kreisfrequenz ω =
2π
T ,
Frequenz ν =
1
T
Offensichtlich gilt:
ẋ(t) = −ωA sin(ωt + α)
|ẋ(t)| ist maximal für ωt + α =
(2n+1)π
,
2
d.h. bei den Durchgängen x(t) = 0.
|ẋ(t)| = 0 für ωt + α = nπ, d.h. bei maximaler Auslenkung.
ẍ(t) = −ω 2 A cos(ωt + α) = −ω 2 x(t)
Die Beschleunigung ist proportional zur Auslenkung und ist ihr entgegengesetzt gerichtet.
26
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Auslenkung einer harmonischen Schwingung genügt der Differentialgleichung
ẍ + ω 2 x = 0
Die Umkehrung gilt ebenfalls: Falls für die Bewegung eines Massenpunktes die Differentialgleichung oben gilt, dann führt der Massenpunkt eine harmonische Schwingung aus,
da
x(t) = A cos(ωt + α) = A1 sin(ωt) + A2 cos(ωt)
die allgemeine Lösung dieser DGL ist.
Oft ist die komplexe Schreibweise zweckmäßig
x(t) = Aeiωt ,
A = |A| eiα
wobei der Realteil die physikalische Schwingung repräsentiert.
Überlagerung harmonischer Schwingungen
Sei x1 (t) = A1 eiωt ,
A1 = |A1 | eiα1
x2 (t) = A2 eiωt ,
A2 = |A2 | eiα2
x(t) = x1 (t) + x2 (t) = (A1 + A2 ) eiωt = Aeiωt
| {z }
A
⇒ Die Überlagerung harmonischer Schwingungen gleicher Richtung und Frequenz ω ist
wieder eine harmonische Schwingung mit Frequenz ω.
27
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
A = |A| eiα ergibt sich aus den Rechenregeln für komplexe Zahlen
q
|A| = |A1 |2 + |A2 |2 + 2 |A1 | |A2 | cos (α2 − α1 )
tan α =
|A1 | sin α1 + |A2 | sin α2
|A1 | cos α1 + |A2 | cos α2
Die Amplitude |A| hängt für festes |A1 | und |A2 | von der Phasendifferenz δ = α2 − α1
ab.
• δ = 2nπ ⇒ |A| = |A1 | + |A2 |
maximaler Wert, konstruktive Interferenz
• δ = (2n + 1)π ⇒ |A| = ||A1 | − |A2 ||
minimaler Wert, destruktive Interferenz
Für die Überlagerung von Schwingungen gleicher Richtung, aber unterschiedlicher Frequenz ist
x(t) = A1 eiω1 t + A2 eiω2 t
keine harmonische Schwingung, sondern ein komplizierterer Vorgang.
Falls
ω1
ω2
=
m
n
mit m, n ∈ N, dann liegt ein periodischer Vorgang vor, dessen Kreisfre-
28
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
quenz ω durch ω1 = mω, ω2 = nω bestimmt ist:
x(t) = A1 eimωt + A2 einωt
!
x(t + T ) = x(t) ⇒ T =
2π
ω
Für |A1 | = |A2 | , ω1 ≈ ω2 ergibt sich ein wichtiger Spezialfall:
A1 = |A1 | eiα1
A2 = |A1 | eiα2
h
i
x(t) = |A1 | ei(ω1 t+α1 ) + ei(ω2 t+α2 )
h
= |A1 | ei[(ω1 −ω2 )t+α1 −α2 ]/2 ei[(ω1 +ω2 )t+α1 +α2 ]/2 + . . .
i
. . . + e−i[(ω1 −ω2 )t+α1 −α2 ]/2 ei[(ω1 +ω2 )t+α1 +α2 ]/2
z =:2ω
}| { z =:2α
}| {
ω1 − ω2
α1 − α2 i[(ω1 + ω2 )t+α1 + α2 ]/2
x(t) = 2 |A1 | cos[(
)t + (
)]e
2 }
2 }
| {z
| {z
=:∆ω
= 2 |A1 | cos(∆ωt + ∆α)e
=:∆α
i(ωt+α)
Für ω1 ≈ ω2 ist ∆ω ω und es liegt eine sogenannte Schwebung vor.
29
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Harmonische Schwingungsanalyse
Oft liegen periodische Vorgänge vor, die nicht in einige wenige harmonische Schwingungen
zerlegt werden können. Hier ist eine Fourierzerlegung oft hilfreich.
x(t) sei eine periodische Funktion mit x(t + T ) = x(t), T =
2π
ω
mit höchstens endlich
vielen Unstetigkeitsstellen.
⇒ x(t) kann in eine Fourier-Reihe entwickelt werden:
∞
X
x(t) =
An einωt
n=−∞
Bestimmung der Fourierkoeffizienten An ?
1
T
tZ
0 +T
−imωt
x(t)e
t0
∞
X
1
dt =
An
T
n=−∞
|
⇒ An =
1
T
Z
tZ
0 +T
ei(n−m)ωt dt
t0
{z
δnm
}
x(t)e−inωt dt
T
Oft nähern die Grundschwingung ∼ eiωt und wenige Oberschwingungen ∼ einωt , n > 1
eine periodische Funktion bereits gut an.
Für T → ∞ geht die Fourier-Reihe in ein Fourier-Integral über
Z
x(t) =
q(Ω)eiΩt dΩ
1
mit q(Ω) =
2π
Z
30
x(t)e−iΩt dt
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Senkrecht zueinander stehende harmonische Schwingungen
Sei x(t) = A cos(ωt + α)
y(t) = B cos(ωt + β) = B cos(ωt + α + |{z}
δ )
β−α
Mit cos(x + y) = cos x cos y − sin x sin y folgt:
y(t) = B(cos(ωt + α) cos δ − sin(ωt + α) sin δ)
|
| r {z
{z
}
}
x(t)
A
1−
y
2
x
⇒
− cos δ =
B A
x2
1− 2
A
x(t)2
A2
sin2 δ
x2
y2
2xy
+
−
cos δ = sin2 δ
2
2
A
B
AB
⇒ Der resultierende Vektor [x(t), y(t)] beschreibt eine Ellipse.
Spezialfälle:
• δ = 0, π
⇒
x
A
∓
y 2
B
=0
y(t) = ± B
A x(t)
Ellipse geht in Gerade über
• δ = π2 , 3π
2 und A = B
⇒ x2 + y 2 = A2
elliptische Schwingung geht in Kreisschwingung über
31
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Für A = B entstehen folgende Figuren:
y
x
Senkrecht zueinander stehende harmonische Schwingungen verschiedener Frequenz geben
Anlaß zu sogenannten Lissajous-Figuren. Die Bewegung ist dabei nur dann streng periodisch und die Bahnkurve nur dann geschlossen, wenn das Frequenzverhältnis
rationale Zahl ist, siehe Beispiele unten:
32
ω1
ω2
eine
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2 Newtonsche Mechanik
2.1 Die Newtonschen Axiome
Die Newtonschen Axiome sind keine mathematisch beweisbaren Sätze, sondern Erfahrungstatsachen, aus denen alle weiteren Sätze über die Dynamik (Bewegung von Körpern
unter Einfluß von Kräften) abgeleitet werden können.
2.1.1 Das Trägheitsgesetz
∧
= 1. Newtonsches Axiom:
Jeder Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, diesen Zustand zu
ändern.
Bemerkungen:
• ist Extraktion vieler Erfahrungen für einen idealen Grenzfall
• Ist nicht unmittelbar experimentell überprüfbar, da wir einwirkende Kräfte nicht
vollständig abschirmen können
• Axiom hat nur dann einen Sinn, wenn es ein Bezugssystem gibt, in dem das Trägheitsgesetz gilt
→Ein solches Bezugssystem heißt Inertialsystem
• Erfahrungsgemäß kann ein im Fixsternhimmel befestigtes Bezugssystem als Inertialsystem betrachtet werden
33
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.1.2 Das Grundgesetz der Dynamik
∧
= 2. Newtonsches Axiom
Es sei m die träge Masse und F~ die Kraft auf einen Körper. Dann gilt:
Die auf einen Massenpunkt wirkende Kraft ist gleich dem Produkt aus Masse und
Beschleunigung des Massenpunkts
m~r¨ = F~
Die ursprüngliche Formulierung von Newton ist etwas anders, für den Impuls p~ = m~r˙
gilt:
Die Änderung des Impulses ist der einwirkenden Kraft proportional und geschieht in
Kraftrichtung
p~˙ = F~
Die beiden Formulierungen sind identisch, falls sich die Masse m während der Bewegung
nicht ändert
d ˙
p~˙ =
m~r = m~r¨ = F~
dt
Für sehr große Geschwindigkeiten (v → c) gilt dies nicht mehr, dann
m0
m= q
1−
v2
c2
mit m0 . . . Ruhemasse (Masse für v = 0)
In diesem Fall m~r¨ 6= F~ , p~˙ = F~ bleibt gültig.
Auch für nichtrelativistische Probleme kann m veränderlich sein (Bsp. Rakete) und
m~r¨ 6= F~ , so dass p~˙ = F~ zur Anwendung kommt.
34
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Dynamische Kraft- und Massenmessung
Wir lassen die gleiche Kraft auf zwei Massenpunkte wirken
⇒ m1 r~¨1 = m2 r~¨2
¨
r~2 m1
= m2
r~¨1 Aus dem Verhältnis der gemessenen Beschleunigungen kann auf das Massenverhältnis
geschlossen werden.
Wir wählen eine Referenzmasse (z.B. das Pariser Urkilogramm).
⇒ Wir können jede Masse eindeutig bestimmen.
Mit der Masseneinheit wird über das Grundgesetz dann die Krafteinheit festgelegt.
1 Newton ist die Kraft, die der Masse 1 kg die Beschleunigung 1 ms−2 erteilt.
1N=1
kg m
s2
Statische Kraft- und Massenmessung
Erfahrungsgemäß ist an einem festen Ort die Fallbeschleunigung ~r¨ = ~g für jeden Körper
die gleiche, g ≈ 9, 81
m
.
s2
Das Gewicht eines Körpers der Masse m ist gegeben durch
F~ = m~g
Das Gewicht des Urkilogramms an dem Ort, wo g = 9, 81
gewählt
1 kp = 9, 81 N
35
m
s2
ist, wird als Kilopond (kp)
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wenn man (mit Hilfe einer beliebigen Waage) bei einer statischen Kraftmessung feststellt,
daß die Gewichte zweier Körper an einem Ort gleich groß sind, dann sind die Massen
ebenfalls gleich
m1 g = m2 g ⇒ m1 = m2
Bei dieser Messung spielt die Trägheit des Körpers keine Rolle, sondern die Schwere ist
entscheidend.
⇒ Wir können zwischen schwerer Masse und träger Masse unterscheiden
Nichttriviale Erfahrungstatsache: beide Arten der Massenbestimmung ergeben dasselbe
Resultat, d.h. schwere Masse = träge Masse.
Bemerkung:
• Grundgesetz der Mechanik gibt Meßvorschrift für Kraft und Masse. Wir können
Kraft- und Massemessungen auf Beschleunigungsmessungen, d.h. Längen- und Zeitmessungen zurückführen.
• Wir können bei bekannter Bahnkurve ~r(t) durch zweimaliges Differenzieren nach
der Zeit für bekannte Masse die wirkende Kraft bestimmen
F~ = m~r¨
• Wir können umgekehrt aus bekannter Kraft F~ die Beschleunigung des Massenpunktes ~r¨ und damit die Bahnkurve gewinnen.
→ typisches Problem der theoretischen und auch der technischen Mechanik
36
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.1.3 Das Wechselwirkungsgesetz
∧
= 3. Newtonsches Axiom (actio=reactio)
Kraftwirkungen sind immer gegenseitig, genau gilt
Die von einem Massenpunkt auf einen zweiten Massenpunkt ausgeübte Kraft F~21 ist
gleich groß und entgegengesetzt der Kraft F~12 , die der zweite Massenpunkt auf den
ersten Massenpunkt ausübt
F~12 = −F~21
2.1.4 Superposition von Kräften
Eine weitere wesentliche Erfahrungstatsache ist der Sachverhalt, daß sich Kräfte vektoriell
addieren.
Kräfte F~1 , F~2 ,. . . auf einen Massenpunkt können durch die Einzelkraft
F~ = F~1 + F~2 + . . .
ersetzt werden, d.h.
m~r¨ = F~1 + F~2 + . . .
2.1.5 Bewegte Bezugssysteme
Die Grundgleichung m~r¨ = F~ ist zunächst in einem Inertialsystem Σ gültig.
Welche Form nimmt die Grundgleichung in einem Bezugssystem Σ0 an, das sich bezüglich
Σ bewegt?
37
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Es gilt:
~r = r~0 + r~0
k
x0 e~0x + y 0 e~0y + z 0 e~0z
de~0y
de~0
de~0
d
dr~0
dx0 ~0
dy 0 ~0
dz 0 ~0
~r˙ = ~r =
+ x0 x + y 0
+ z0 z +
ex +
ey +
e
dt
dt
dt
dt
dt
dt{z
dt }z
|dt
˙
r~0
˙
mit r~0 ≡
d0 r~0
dt
als Geschwindigkeit des Massenpunktes für einen Beobachter in Σ0 , für den
die Achsenrichtungen fest scheinen
d0 r~0
dt
→ Differentiation in Σ0 bei fester Lage der Koordinatenachsen.
d~r
. . . Absolutgeschwindigkeit
dt
d0 r~0
v~0 ≡
. . . Relativgeschwindigkeit
dt
dr~0
v~tr ≡
. . . Translationsgeschwindigkeit, Geschwindigkeit von O’ in Σ
dt
~v ≡
Die zeitliche Änderung der Basisvektoren e~0x , e~0y und e~0z resultiert aus einer möglichen
Drehung des Systems Σ0 um eine Achse durch O0 .
38
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir betrachten die Drehung um eine Achse:
# »
# » # »
d AB = CB dϕ = AB sin θdϕ
# »
d AB dt
# »
dϕ
= AB sin θ
dt
k
ω
ω . . . momentane Winkelgeschwindigkeit
Wir definieren den Vektor der Winkelgeschwindigkeit ω
~ durch die Richtung der Achse
einer Rechtsschraube und den Betrag |~
ω | = ω = |ϕ̇|.
Damit gilt
# »
dAB
# »
=ω
~ × AB
dt
Speziell folgt
de~0x
=ω
~ × e~0x ,
dt
de~0y
=ω
~ × e~0y ,
dt
39
de~0z
=ω
~ × e~0z
dt
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
und damit
x0
de~0y
de~0x
de~0
+ y0
+ z0 z = ω
~ × r~0
dt
dt
dt
Das bedeutet für die Geschwindigkeit
d~r
d0 r~0
=
+
dt
dt
dr~0
+ω
~ × r~0
dt
|
{z
}
(∗)
„Führungsgeschwindigkeit“
gilt ~r − r~0 = r~0
⇒
dr~0
d0 r~0
=
+ω
~ × r~0
dt
dt
(∗∗)
Offensichtlich gilt obige Beziehung für jeden Vektor ~b = b0x e~0x + b0y e~0y + b0z e~0z in Σ0
d.h.
d0~b
d~b
=
+ω
~ × ~b
dt
dt
(∗ ∗ ∗)
Speziell für ~b = ω
~ gilt dann
d~
ω
d0 ω
~
=
dt
dt
d.h. der Vektor der Winkelgeschwindigkeit spielt eine besondere Rolle, seine zeitliche
Änderung ist in beiden Bezugssystemen die gleiche.
Wir berechnen jetzt die Beschleunigung durch Differentiation von (∗):
d~v
dv~0 dv~tr
dr~0 d~
ω ~0
=
+
+ω
~×
+
×r
dt
dt
dt
dt
dt
Mit
dv~0 (∗∗∗) d0 v~0
=
+ω
~ × v~0
dt ~b=v~0 dt
40
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
und
dr~0 (∗∗) d0 r~0
=
+~
ω × r~0
dt
dt
|{z}
v~0
ergibt sich
d~v
d0 v~0
dv~tr
d~
ω ~0
=
+ω
~ × v~0 +
+ω
~ × v~0 + ω
~ × (~
ω × r~0 ) +
×r
dt
dt
dt
dt
d.h.
d~v
d0 v~0 dv~tr
d~
ω ~0
=
+
+
×r +ω
~ × (~
ω × r~0 ) + 2~
ω × v~0
dt
dt
dt
dt
dv~tr
dt
. . . Translationsbeschleunigung
dv~tr
dt
+
d~
ω
dt
(∗ ∗ ∗∗)
× r~0 + ω
~ × (~
ω × r~0 ) . . . Führungsbeschleunigung
(ist gerade die zeitliche Ableitung der Führungsgeschwindigkeit für verschwindende Relativgeschwindigkeit v~0 = 0)
−2~
ω × v~0 . . . Coriolisbeschleunigung
−~
ω × (~
ω × r~0 ) . . . Zentrifugalbeschleunigung
In Σ gilt die Grundgleichung der Mechanik m~r¨ = F~ .
~r¨ =
d~v
dt
haben wir gerade berechnet (∗ ∗ ∗∗).
0 ~0
¨
In Σ0 messen wir die Beschleunigung r~0 = ddtv , dafür gilt nach (∗ ∗ ∗∗) eine modifizierte
Grundgleichung:
¨
˙
mr~0 = F~ −mr~¨0 − mω
~˙ × r~0 − m~
ω × (~
ω × r~0 ) − 2m~
ω × r~0
|
{z
}
4 Trägheitskräfte
Ist speziell F~ = 0 so wird mittels der Trägheitskräfte gerade der Effekt der Trägheit
eines Massenpunkts beschrieben, wonach ein sich selbst überlassener Massenpunkt sich
(im Inertialsystem Σ) beschleunigungsfrei bewegt.
41
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
⇒ Die Grundgleichung der Mechanik kann in jedem Bezugssystem angewendet werden,
wenn zu der Kraft, die am Massenpunkt im Inertialsystem angreift, die Trägheitskräfte
addiert werden.
Beispiele
Zentrifugalkraft
Corioliskraft
42
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Trägheitskräfte sind nicht wirkliche Kräfte in dem Sinne, daß sie von umgebenden materiellen Körpern ausgehen, sondern sind durch die Wahl des Bezugssystems bestimmt.
⇒ Sie werden daher auch als „Scheinkräfte“ bezeichnet, im Unterschied zu den als „eingeprägte Kräfte“ bezeichneten wirklichen Kräften.
In Σ0 sind Scheinkräfte genauso meßbar wie eingeprägte Kräfte.
Sei speziell Σ ein Inertialsystem und Σ0 führe bezüglich Σ eine gleichförmig geradlinige
Bewegung aus, d.h.
~r = r~0 + r~0 ,
r~˙0 = const.,
ω
~ =0
(G)
Dann verschwinden offensichtlich die Trägheitskräfte und es gilt
in Σ : m~r¨ = F~
¨
in Σ0 : mr~0 = F~
D.h. Σ0 ist ebenfalls ein Inertialsystem. Weiters ist jedes System Σ0 , das relativ zu Σ eine
unbeschleunigte Translationsbewegung ausführt, ein Inertialsystem. Mit keinem mechanischen Experiment kann zwischen Σ und Σ0 unterschieden werden.
⇒ Wir können keine absolute Ruhe und keine absolute Geschwindigkeit feststellen.
Die zwischen Σ und Σ0 vermittelnde Transformation (G) wird als Galilei-Transformation
bezeichnet und der obige Sachverhalt als Galilei’sches Relativitätsprinzip:
Die Grundgleichung der Mechanik ist unter Galilei-Transformationen beim Übergang
von einem Inertialsystem zu einem anderen forminvariant.
Bemerkung: Charakteristisch für die Galilei-Transformation ist, daß die Zeit nicht transformiert wird (t = t0 )
Diese Forderung ist nicht trivial und auch nicht universell gültig, gilt nur
solange die Translationsgeschwindigkeit vtr c . . . Lichtgeschwindigkeit
43
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.2 Dynamik eines Massenpunktes
2.2.1 Bewegungsgleichungen
Die Masse m des Massenpunktes und die auf ihn wirkende Gesamtkraft F~ seien bekannt,
die gesuchte Bahnkurve genügt der Grundgleichung
m~r¨ = F~ (~r, ~r˙, t)
(Die Kraft F~ ist im Allgemeinen eine Funktion von Ort, Geschwindigkeit und Zeit)
In Komponenten zerlegt ergeben sich die
Bewegungsgleichungen des Massenpunktes
mẍ = Fx (x, y, z, ẋ, ẏ, ż, t)
mÿ = Fy (x, y, z, ẋ, ẏ, ż, t)
mz̈ = Fz (x, y, z, ẋ, ẏ, ż, t)
D.h. es ergeben sich 3 gekoppelte Differentialgleichungen.
Die allgemeine Lösung enthält 6 Integrationskonstanten. Diese können z.B. durch Anfangsbedingungen r~0 = ~r(t0 ), v~0 = ~r˙ (t0 ) festgelegt werden.
Bei bekanntem Kraftgesetz F~ = F~ (~r, ~r˙, t) und bekannten Anfangsbedingungen ist der
Ablauf der Bewegung des Massenpunktes eindeutig bestimmt.
→ „Kausalität im mechanischen Geschehen“
Die Integration der Bewegungsgleichungen kann durch die Einführung geeigneter Größen
wie Impuls, Drehimpuls, Energie und den dafür geltenden Erhaltungssätzen erleichtert
werden.
44
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.2.2 Impulsbilanz
Impuls des Massenpunktes:
d
p~ = m~r˙ |
dt
p~˙ = m~r¨ = F~
⇒ Die zeitliche Änderung des Impulses ist gleich der einwirkenden Kraft.
F~ = 0
⇒
d~
p
=0
dt
⇒
p~ = const.
Bereits bekanntes Ergebnis: Ein kräftefreier Massenpunkt ruht oder bewegt sich gleichförmig entlang einer Geraden.
Bemerkung: Für Systeme aus mehreren Massenpunkten ist die Impulsbilanz nicht trivial.
2.2.3 Energiebilanz
Für eine hinreichend kleine Verschiebung ist die infinitesimale Arbeit dW definiert als
dW = F~ · d~r = |F~ ||d~r| cos ϕ
45
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die gesamte Arbeit W , die von F~ bei Verschiebung eines Massenpunktes längs der Kurve
C von P1 nach P2 zu verrichten ist, hängt i.A. von Anfangs- und Endpunkt sowie der
Wegführung ab:
Z
F~ · d~r
W =
C
Die Leistung P ist definiert als Arbeit pro Zeiteinheit:
P =
dW
d(F~ · ~r)
=
= F~ · ~r˙
dt
dt
Wir multiplizieren die Bewegungsgleichung m~r¨ = F~ mit ~r˙ :
m~r¨ · ~r˙ = F~ · ~r˙
d
dt
mit
k
1
m
~
r˙
2
k
·~
r˙
P
1 ˙ ˙ 1 ˙2
m~r · ~r = m|~r| := T
2
2
T . . . Bewegungsenergie oder kinetische Energie.
⇒ Damit erhalten wir die Bilanzgleichung für die kinetische Energie:
dT
=P
dt
Die zeitliche Änderung der kinetischen Energie ist gleich der Leistung der einwirkenden
Kraft.
Integration der Bilanzgleichung
Z2
Z2
dT =
1
Z2
P dt =
1
1
F~ · |{z}
~r˙ dt =
d~
r
k
T2 − T1
46
Z2
1
F~ · d~r = W
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Konservative Kraftfelder
Eine Kraft heißt konservativ, wenn F~ = F~ (~r) ist und es eine skalare Funktion U (~r) gibt,
so daß gilt
~ (~r)
F~ = −∇U
~ (~r) = ∂U g~i ,
d.h. (vgl. 1.2) ∇U
∂xi
⇒ Fi = −
F~ = Fi g~i
∂U
∂xi
Speziell in kartesischen Koordinaten
Fx = −
∂U
,
∂x
Fy = −
∂U
,
∂y
Fz = −
∂U
∂z
Für konservative Kraftfelder gilt also für die Leistung
i
~ · ~r˙ = − ∂U dx = − dU
P = F~ · ~r˙ = −∇U
k
∂xi dt
dt
dT
dt
⇒
d
(T + U ) = 0
dt
Damit erhalten wir den Energieerhaltungssatz
1
T + U = m|~r˙ |2 + U (~r) =: E = const.
2
U heißt potentielle Energie oder auch Potential und E ist als Summe aus kinetischer und
potentieller Energie die mechanische Gesamtenergie des Massenpunktes.
47
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wann besitzt eine Kraft ein Potential?
~ (~r) |∇×
~
F~ = −∇U
~ × F~ = −∇
~ × ∇U
~ =0
∇
~ × F~ = 0, d.h. die Wirbelfreiheit des Kraftfelds ist notwendige Bedingung für die
⇒∇
Existenz eines Potentials.
~ gilt
Falls F~ = −∇U
ZP2
P1
F~ · d~r = −
ZP2
~ · d~r = −
∇U
ZP2
dU = U1 − U2
(Ui = U (Pi ))
P1
P1
d.h. die Arbeit ist wegunabhängig. Speziell für eine geschlossene Kurve gilt
Z
F~ · d~r =
I
F~ · d~r = 0
C
Nun gilt für einfach zusammenhängende Gebiete der Stokes’sche Satz
Z
C
F~ · d~r =
Z ~ × F~ · dA
~
∇
A
wobei A eine beliebige, von C umrandete Fläche bedeutet.
48
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
D.h. Unabhängigkeit des Wegintegrals der Kraft von der durchlaufenen Kurve (und damit die Existenz eines Potentials) ist äquivalent zur Wirbelfreiheit der Kraft.
⇒ Die Wirbelfreiheit der Kraft ist notwendige und hinreichende Bedingung für die Existenz eines Potentials.
Wir bestimmen U (~r) aus dem Wegintegral der Kraft
ZP
U (~r) = U (r~0 ) −
F~ (r~0 ) · dr~0
P0
~ (~r) = −F~ (~r) gilt.
Zu zeigen, daß dann ∇U
Beweis: Wir können wegen der Wegunabhängigkeit des Integrals eine spezielle Streckenführung wählen (C → C 0 ):
Zx
U (x, y, z) = U (x0 , y0 , z0 ) −
0
0
Zy
Fx (x , y0 , z0 )dx −
x0
∂U
= −Fx (x, y0 , z0 ) −
∂x
0
y0
∂Fy (x, y 0 , z0 ) 0
dy −
∂x
|
{z
}
∂Fx (x,y 0 ,z0 )
∂y 0
Zz
Fy (x, y , z0 )dy −
y0
Zy
0
Fz (x, y, z 0 )dz 0
z0
Zz
z0
∂Fz (x, y, z 0 ) 0
dz
∂x
|
{z
}
∂Fx (x,y,z 0 )
∂z 0
~ × F~ = 0)
(Die Ausdrücke unter den geschweiften Klammern ergeben sich mit ∇
∂U
= −Fx (x, y0 , z0 )−Fx (x, y, z0 ) +Fx (x, y0 , z0 )−Fx (x, y, z)+Fx (x, y, z0 ) = −Fx (x, y, z)
::::::::::
::::::::::
∂x
49
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Analog läßt sich zeigen
∂U
= −Fy (x, y, z)
∂y
∂U
= −Fz (x, y, z)
∂z
~ (~r) = −F~ (~r)
d.h. ∇U
Damit haben wir eine Rechenvorschrift für das Potential gefunden. Das Potential ist nur
!
bis auf eine Konstante bestimmt, wir setzen U (r~0 ) = 0 und erhalten
ZP
U (~r) = −
F~ (r~0 ) · dr~0 =
P0
ZP0
F~ (r~0 ) · dr~0
P
häufig P0 = P (r~0 ) = P (∞)
∧
„Äquipotentialflächen“ = Flächen gleichen Potentials
~
U = const. ⇒ dU = 0 ⇒ d~r⊥∇U
k
~ · d~
∇U
r
~ steht senkrecht auf der Äquipotentialfläche, es gibt keine Kraftd.h. der Gradient ∇U
komponenten in dieser Fläche.
⇒ auf Äquipotentialflächen bewegt sich der Massenpunkt kräftefrei
Wir betrachten speziell eine Kraft F~ , die orthogonal zu ~r˙ steht:
P = F~ · ~r˙ = 0
⇒ T = const.
k
dT
dt
50
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Hier ist die potentielle Energie ebenfalls konstant, da die Ortsänderung senkrecht zur
Kraft, d.h. der Potentialänderung verläuft.
Typisches Beispiel: Lorentzkraft auf elektrische Ladung q im Magnetfeld B.
~ ⇒ F~ · ~r˙ = 0
F~ = q~r˙ × B
nichtkonservative Kräfte
Sei F~ ein zeitabhängiges Kraftfeld, F~ = F~ (~r, t)
~ × F~ (~r, t) = 0 ∀t
Sei ∇
⇒ wir finden ein zeitabhängiges Potential U (~r, t) mit
~ (~r, t)
F~ (~r, t) = −∇U
Ist das Kraftfeld energieerhaltend? Wir untersuchen
i
dT
~ · ~r˙ = − ∂U dx − ∂U + ∂U
= F~ · ~r˙ = −∇U
i
dt
∂t} ∂t
{z
| ∂x dt
− dU
dt
⇒
d
∂U
(T + U ) =
dt
∂t
d.h. die zeitliche Änderung der mechanischen Energie ist bestimmt durch die Zeitableitung von U .
Kräfte, die die Energie eines Massenpunktes nicht erhalten, werden als „dissipative Kräfte“ bezeichnet
• Kräfte, die von Zeit oder Geschwindigkeit abhängen
• ortsabhängige Kräfte, die nicht wirbelfrei sind
51
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Im Allgemeinen unterliegen Massenpunkte sowohl konservativen als auch dissipativen
Kräften
F~ = F~ (cons) (~r) +F~ (diss) (~r, ~r˙, t)
| {z }
~ (~
−∇U
r)
und es gilt die verallgemeinerte Energiebilanz
d
(T + U ) = P (diss) = F~ (diss) · ~r˙
dt
die z.B. die Umwandlung mechanischer Energie in Reibungswärme umfaßt.
Beispiel: Schwerkraft
Oberflächennah ist das Gravitationsfeld der Erde homogen
F~ = −mg e~z
Zz
zugehöriges Potential: U (x, y, z) = −
0
0
Zz
dz Fz (x, y, z ) =
0
dz 0 mg = mgz
0
damit Energieerhaltung
1
mv 2 + mgz = E = const.
2 k
ẋ2 + ẏ 2 + ż 2
Bewegt sich der Massenpunkt in Luft, kommt noch eine dissipative Reibungskraft F~ (diss)
hinzu, approximativ gilt
F~ (diss) = −γ~r˙
γ . . . Reibungs-, Dämpfungskoeffizient
52
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
dann gilt für die mechanische Energie
1
E = mv 2 + mgz
2
die Bilanzgleichung
dE
= −γv 2
dt
⇒ Die mechanische Energie nimmt ständig ab, wird in Wärme umgewandelt.
Beispiel: Linearer harmonischer Oszillator
Für kleine Auslenkungen gilt für die rücktreibende Kraft
F~ = −kxe~x
k > 0 . . . Federkonstante
Damit folgt die Bewegungsgleichung
mẍ = −kx
ẍ + ω 2 x = 0
mit ω 2 =
k
m
(Die Differentialgleichung wurde in 1.4 bereits gelöst)
Zx
U (x) =
1
dx0 kx0 = kx2 ,
2
0
53
konservative Kraft
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit Energieerhaltung
1
1
mẋ2 + kx2 = E = const.
2
2
Für eine reale Feder kommt es zu dissipativen Effekten (innere Reibung)
F~ (diss) = −γ ẋe~x
damit Bewegungsgleichung
mẍ = −kx − γ ẋ
und Bilanzgleichung
dE
= −γ ẋ2
dt
d.h. das System kommt zur Ruhe.
Verallgemeinerung auf einen isotropen 3D-Oszillator:
F~ = −k~r
m~r¨ = −k~r
1
1
U (~r) = k|~r|2 = kr2
2
2
2.2.4 Drehimpulsbilanz
Wir starten von der Bewegungsgleichung
m~r¨ = F~
|~r×
m~r × ~r¨ = ~r × F~ , wegen
d ~r × ~r˙ = ~r˙ × ~r˙ +~r × ~r¨
| {z }
dt
0
folgt
d
m~r × ~r˙ = ~r × F~
dt | {z } | {z }
~
=:L
~
=:M
54
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
~ . . . Drehimpuls
L
~ . . . Drehmoment
M
⇒ Die zeitliche Änderung des Drehimpulses ist gleich dem einwirkenden Drehmoment
~
dL
~
=M
dt
~ = 0 gilt die Drehimpulserhaltung
Für M
~
dL
~ = const.
=0⇒L
dt
~ = 0 gilt
M
• offensichtlich immer für den trivialen Fall F~ = 0
• für F~ 6= 0, falls F~ und ~r parallel oder antiparallel stehen, derartige Kräfte heißen
Zentralkräfte, in allgemeinster Form
~r
F~ = f (~r, ~r˙, t)
|~r|
Die Drehimpulserhaltung gilt also genau dann, wenn sich der Massenpunkt unter dem
Einfluß einer Zentralkraft bewegt.
Betrachten Bewegung eines Massenpunktes entlang einer Bahnkurve:
⇒ Die zeitliche Änderung der „Flächengeschwindigkeit“
55
~
dA
dt
ist proportional zum Dre-
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
himpuls.
~
~ = const. ⇒ dA = const.
L
dt
(bekannt als „Flächensatz“)
D.h. für einen Massenpunkt unter Wirkung einer Zentralkraft gilt:
• die Bewegung erfolgt in einer Ebene senkrecht zum Drehimpuls
• der Radiusvektor („Fahrstrahl“) überstreicht in gleichen Zeiten gleiche Flächen
~ = m~r × ~r˙ = Le~z , d.h. die Bewegung vollziehe sich in der x-y-Ebene. Dann ist
Sei L
~ = m(xẏ − y ẋ)e~z
L
und für die Drehimpulserhaltung gilt
xẏ − y ẋ = const.
Wir gehen über zu Polarkoordinaten
~r = ρe~ρ
~r˙ = ρ̇e~ρ + ρϕ̇e~ϕ
(vgl. 1.2)
~ = m~r × ~r˙ = mρ2 ϕ̇e~z
L
56
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Flächengeschwindigkeit
dA
1 ~ 1 2
~
=
L = ρ ϕ̇ = const.
dt 2m
2
Bemerkung: Als Zentralkräfte im engeren Sinne bezeichnet man Kräfte der Form
~r
F~ = f (r)
r
Ein solches Zentralkraftfeld ist konservativ und besitzt das Potential
Zr
U (r) = −
dr0 f (r0 )
r0
Speziell für f (r) = − rα2 (Gravitations-, Coulombkraft) lautet das Potential
(r0 → ∞)
U (r) = −
α
r
⇒ Für die Bewegung eines Massenpunktes unter dem Einfluß einer Zentralkraft im engeren Sinne gelten Drehimpuls- und Energieerhaltung.
2.2.5 Erhaltungssätze und Integration der Bewegungsgleichungen
Wir betrachten zunächst eine eindimensionale Bewegung entlang x. Offensichtlich gilt
~ = 0 (L
~ = m~r × ~r˙ ).
L
Für eine konservative Kraft
F~ = F (x)e~x
gilt die Energieerhaltung
1
mẋ2 + U (x) = E = const.
2
57
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Zx
mit U (x) = −
dx0 F (x0 )
x0
2
[E − U (x)]
m
r
dx
2
ẋ =
=
[E − U (x)]
dt
m
dx
dt = p
2[E − U (x)]/m
ẋ2 =
Z
t=
dx
p
+ const.
2[E − U (x)]/m
Energie und Integrationskonstante bestimmen die beiden freien Konstanten in der Bewegungsgleichung mẍ = F (x).
Die Gleichung oben liefert t(x), deren Umkehrung x(t).
Wegen ẋ2 ≥ 0 muss E − U (x) ≥ 0 gelten, d.h. Bewegung nur in solchen Gebieten, wo
U (x) ≤ E
Für Punkte, in denen U (x) = E gilt, kehrt die Geschwindigkeit ihr Vorzeichen um.
→ „Umkehrpunkte“, hier x1 , x2 , x3
Wenn das erlaubte Gebiet durch Umkehrpunkte begrenzt wird, ist die Bewegung „finit“.
58
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Oben erfolgt eine finite Bewegung zwischen x1 und x2 . Dort findet eine periodische, aber
im Allgemeinen nicht harmonische Bewegung statt.
Im Bereich x > x3 ist die Bewegung „infinit“, der Massenpunkt kommt aus dem Unendichen, wird bei x3 reflektiert und läuft wieder ins Unendliche.
Mögliche Ruhelagen sind die Stellen, wo keine Kraft auf den Massenpunkt wirkt
dU
= 0,
dx
also die Extrema des Potentials.
Minimum von U → stabile Ruhelage
Maximum von U → labile Ruhelage
Wir betrachten jetzt eine dreidimensionale Bewegung im Zentralkraftfeld
⇒ Drehimpulserhaltung und Energieerhaltung
~r
F~ = f (r)
r
Die vektorielle Bewegungsgleichung lautet:
m~r¨ = f (r)
~r
r
Das Potential erhalten wir aus
Zr
U (r) = −
dr0 f (r0 )
r0
59
(vgl. 2.2.4)
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
~ = const. erfolgt eine Bewegung in einer Ebene. Ohne Beschränkung der AllgeFür L
meinheit verlaufe die Bewegung in der x-y-Ebene, wir gehen dort zu Polarkoordinaten
über
~r = ρe~ρ
~r˙ = ρ̇e~ρ + ρϕ̇e~ϕ
(vgl. 1.2)
Die Erhaltungssätze liefern
mρ2 ϕ̇ = L
1
2
2 2 + U (ρ) = E
2 m ρ̇ + ρ ϕ̇
ϕ̇ =
damit
1
mρ̇2 +
2
L
mρ2
L2
+ U (ρ)
2mρ2
|
{z
}
=E
Ueff ... effektives Potential
Damit erhalten wir eine analoge Gleichung wie vorhin für die eindimensionale Bewegung
(x → ρ)
1
E = mρ̇2 + Ueff (ρ)
2
2
2
ρ̇ =
[E − Ueff (ρ)]
m
r
2
dρ
ρ̇ =
=
[E − Ueff (ρ)]
dt
m
dρ
dt = p
2 [E − Ueff (ρ)] /m
60
(∗)
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Z
t=
dρ
p
+ const.
2 [E − Ueff (ρ)] /m
⇒ aus t(ρ) erhalten wir die Umkehrfunktion ρ(t) und daraus ϕ(t) wie folgt:
Wegen ρ = ρ[ϕ(t)] gilt
dρ dϕ
dρ L
dρ
=
=
dt
dϕ dt
dϕ mρ2
r
dρ
mρ2 dρ ∗ mρ2 2
=
⇒
=
[E − Ueff (ρ)]
dϕ
L dt
L
m
L
dρ
p
⇒ dϕ =
2
mρ
2[E − Ueff (ρ)]/m
L
⇒ϕ=
m
Z
dρ
p
+ const.
ρ2 2[E − Ueff (ρ)]/m
⇒ ϕ(ρ) → ϕ(t)
k
ρ(t)
Damit sind die Bewegungsgleichungen in allgemeiner Form gelöst.
ϕ ändert sich monoton mit der Zeit, da ϕ̇ =
L
mρ2
niemals das Vorzeichen wechselt.
für L = 0 ⇒ ϕ̇ = 0 ⇒ Spezialfall einer eindimensionalen Bewegung
Der Radialteil der Bewegung kann immer als eindimensionale Bewegung im effektiven
Potential
Ueff (ρ) = U (ρ) +
L2
2mρ2
| {z }
„Zentrifugalenergie“,
„Zentrifugalbarriere“
aufgefaßt werden.
61
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Grenzen des Bewegungsbereichs sind bestimmt durch
ρ̇ = 0 ⇒ Ueff (ρ) = U (ρ) +
L2
=E
2mρ2
Dort ist die radiale Geschwindigkeit ρ̇ = 0, aber der Massenpunkt hält nicht an, da
ϕ̇ =
L
mρ2
6= 0 für L 6= 0
Falls der Bewegungsbereich durch ρmin und ρmax eingeschränkt ist, ist die Bewegung
finit, die Bahn verläuft in einem ringförmigen Gebiet.
62
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Bahn muß nicht geschlossen sein! Es gibt nur 2 Typen von Zentralfeldern, in denen
alle Bahnen finiter Bewegungen geschlossen sind, nämlich
U (ρ) ∼
1
ρ
U (ρ) ∼ ρ2
Falls der zulässige ρ-Bereich Ueff (ρ) ≤ E nur durch ρ ≥ ρmin eingeschränkt wird, ist die
Bewegung des Massenpunktes infinit. Der Massenpunkt kommt aus dem Unendlichen
und geht wieder ins Unendliche.
2.2.6 Spezielle Probleme
A) Bewegung auf der rotierenden Erde
Im rotierenden Bezugssystem wirken auf Massenpunkte zusätzlich zur eingeprägten Kraft
noch die
Zentrifugalkraft Fcen = −m~
ω × (~
ω × ~r)
und Corioliskraft Fcor = −2m~
ω × ~r˙ (vgl. 2.1.5)
Dabei ist ω die Winkelgeschwindigkeit der Erde gegenüber dem Fixsternhimmel
ω = |~
ω| =
2π
s−1
86164
Wir betrachten einen Körper, auf den im Inertialsystem nur die Gravitation der Erde
wirkt. Für den irdischen Beobachter wirkt die Schwerkraft, die die Gravitationskraft der
Erde und die Zentrifugalkraft zusammenfaßt.
63
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir müssen noch die Corioliskraft separat berücksichtigen, damit
m~r¨ = m~g + 2m~r˙ × ω
~
~g enthält den Einfluß der Zentrifugalkraft:
Offensichtlich ändert sich ~g infolge der Zentrifugalkraft mit der geographischen Breite θ
Äquator |~g | = 9, 78 ms−2
Pol |~g | = 9, 83 ms−2
Bemerkung: Es existieren weitere Einflüsse auf ~g infolge der Asymmetrie der Erde, der
inhomogenen Dichte der Erde und anderer Himmelskörper.
64
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir wählen als Bezugssystem ein kartesisches Koordinatensystem bei der geographischen
Breite θ
In diesem Koordinatensystem gilt
~g = −g e~z (näherungsweise)
~r˙ = ẋe~x + ẏ e~y + ż e~z
ω
~ = −ω cos θe~x + ω sin θe~z
aus m~r¨ = m~g + 2m~r˙ × ω
~ wird
ẍ = 2ω sin θẏ
ÿ = −2ω sin θẋ − 2ω cos θż
z̈ = −g + 2ω cos θẏ
Wir lösen diese Gleichungen jetzt für den freien Fall. Anfangsbedingungen:
t = 0,
x = y = 0,
z = h,
65
ẋ = ẏ = ż = 0
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik


ẋ ∼ ω  wegen ω klein können wir Terme

ẏ ∼ ω  quadratisch in ω vernachlässigen
d.h. ẍ ∼ ω 2 → 0
ÿ → −2ω cos θż
z̈ → −g
Jetzt mit den Anfangsbedingungen:
x(t = 0) = 0,
ẋ(t = 0) = 0,
ẍ = 0
⇒ x(t) = 0
z(t = 0) = h,
ż(t = 0) = 0,
z̈ = −g
⇒ ż = −gt
1
⇒ z = h − gt2
2
damit in ÿ = −2ω cos θż = 2gtω cos θ
mit ẏ(t = 0) = 0 ⇒ ẏ = gt2 ω cos θ
1
mit y(t = 0) = 0 ⇒ y = gt3 ω cos θ
3
y zeigt nach Osten, d.h. der fallende Körper erfährt eine Ostabweichung. Die Ostablenkung ist eine Folge der höheren Rotationsgeschwindigkeit der Erde in der Abwurfhöhe
gegenüber der Rotationsgeschwindigkeit an der Erdoberfläche. Mit entsprechenden Fallexperimenten kann ab etwa 1800 die Drehung der Erde um ihre eigene Achse empirisch
nachgewiesen werden.
66
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wirkung der Corioliskraft
Wir zerlegen den Vektor der Winkelgeschwindigkeit in Vertikal- und Horizontalkomponenten
Bewegt sich ein Körper horizontal, so gibt ω
~ v Anlaß zu einer horizontalen Kraft orthogonal zu ~v
F~cor = −2m~
ω × ~v
(Rechte-Hand-Regel anwenden)
⇒ Bahnabweichung nach rechts/links auf nördlicher/südlicher Halbkugel
Weiters gibt ω
~ h Anlaß zu einer Kraft, die bei horizontaler Bewegung nach oben oder
unten zeigt
⇒ Gewichtsänderung des Körpers (Eötvös-Effekt). Dieser Effekt wurde von Baron Roland
von Eötvös um 1900 bei der Auswertung von Gravitationsmessungen mittels bewegter
Schiffe im Atlantik festgestellt und erklärt.
67
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
B) Kepler-Problem
Wir betrachten die Bewegung einer Punktmasse m im Gravitationsfeld einer als raumfest
angenommenen Punktmasse M (Approximation der Planetenbewegung um die Sonne).
Die Gravitationskraft bestimmt die Bewegungsgleichung
m~r¨ = F~ = −γ
mM
~r
r3
γ . . . Gravitationskonstante, γ = 6, 67 · 10−11
m3
kgs2
F~ . . . konservativ, Zentralkraft
⇒ Energie- und Drehimpulserhaltung
Ueff = −γ
mM
L2
+
(vgl. 2.2.5)
r
2mr2
Wir suchen das Minimum von Ueff :
mM
L2
1
dUeff L2
=
0
=
γ
−
=
γmM
−
dr r=r0
mr0
r02
mr03
r02
⇒ r0 ≡ k =
68
L2
γm2 M
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Ueff (r = k) = −γ
mM
L2
γ 2 m3 M 2
2
2 4
2
·
γm
M
+
·
γ
m
M
=
−
L2
2mL4
2L2
finite Bewegung für Ueff (k) ≤ E < 0
γ 2 m3 M 2
≤E<0
2L2
γmM
mit L2 = kγm2 M → −
≤E<0
2k
2Ek
−1 ≤
< 0 (*)
γmM
⇒−
infinite Bewegung für 0 ≤ E
Die Umkehrpunkte erhalten wir aus Ueff (r) − E = 0
γmM
L2
−
−E =0
2mr2
r
1
γm2 M 1 2mE
−
2
−
=0
2
2
r2
L
r
L
| {z }
d.h.
1
k
1
21
1
L2
2mE
−
−
k
·
·
=0
r2 k r k2
γm2 M L2
| {z }
k
21
1 2Ek
1
−
−
=0
r2 k r k 2 γmM
1
1
= ±
r
k
s
1
1 2Ek
1
+ 2
=
2
k
k γmM
k
s
:=
1+
mit (*): finite Bewegung für 0 ≤ < 1
infinite Bewegung für E ≥ 0, d.h. ≥ 1
69
s
1±
2Ek
γmM
2Ek
1+
γmM
!
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Umkehrpunkte
1
=
rmin
1+
k
1
rmax
1−
k
=
( < 1)
für → 1 ⇒ rmax → ∞
Bahngleichung r(ϕ)?
2
m {E
Erinnerung 2.2.5: ṙ2 =
− Ueff (r)}
dr
=
⇒ ṙ =
dt
r
2
{E − Ueff (r)}
m
r ist abhängig vom Bahnwinkel ϕ: r = r(ϕ(t))
dr dϕ
dr L
dr
=
=
dt
dϕ dt
dϕ mr2
(mit L = mr2 ϕ̇ (2.2.4))
dr
mr2 dr
mr2
⇒
=
=
dϕ
L dt
L
r
2
{E − Ueff (r)}
m
L
dr
p
2
mr
2{E − Ueff (r)}/m
Z
L
dr
p
ϕ=
+ const.
2
m
r 2{E − Ueff (r)}/m
dϕ =
spezielle Anfangsbedingung: ϕ = 0 für r = rmin , damit
L
ϕ=
m
Zr
rmin
Zr
dr0
p
=
r0 2 2{E − Ueff (r0 )}/m
rmin
dr0
r0 2
q
2m
{E
L2
− Ueff (r0 )}
Wir ersetzen L und E durch und k
s
=
1+
2Ek
2 − 1
2E
2E γm2 M
⇒
=
=
γmM
k2
γmM k
γmM L2
70
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
D.h.
2 −1
k2
=
2mE
.
L2
Damit:
2m
2 − 1 2m γmM 2m L2
0
− 2
{E
−
U
(r
)}
=
+ 2
eff
0
02
L2
k2
|L {zr } |L 2mr
{z }
2
kr 0
1
r0 2
2 − 1 2 1
1
+
−
k2
k r0 r0 2
2
1
1 2
= 2−
−
k
r0 k
(
)
2
k 1
1 2
= 2 1−
−
k
r0 k
=
Zr
damit ϕ =
rmin
r0 2 k
q
1−
dr0
k
1
r0
−
k
=
1 2
k
Zr
rmin
dr0
r0 2
)− 21
k 1
1 2
1−
−
r0 k
(
Variablensubstitution
k
1
1
−
r0 k
=z⇒
z(rmin ) =
dz
k 1
= − 02
dr0
r
0
dr
2 = − k dz
0
r
k 1
1
−
=1
rmin k
| {z }
1+
k
k
(Zr1 − k1 )
damit ϕ = −
1
√
dz
k 1 1
= arccos
−
r k
1 − z2
k
⇒ cos ϕ =
⇔
1
1
= (1 + cos ϕ)
r
k
1 1
−
r k
Kegelschnittgleichung
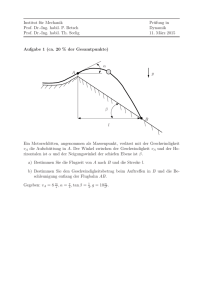
71
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
• Kreis
= 0 ⇔ E = −γ
mM
2k
• Ellipse
0 < < 1 ⇔ −γ
mM
<E<0
2k
• Parabel
=1⇔E=0
• Hyperbel
>1⇔E>0
Bahnkurve ~r(t)?
Wir kennen die Bahngleichung
r = r(ϕ) =
k
.
1 + cos ϕ
Mit L = mr2 ϕ̇ = mr2
72
dϕ
dt
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
m
m
folgt dt = r2 dϕ ⇒ t − t0 =
L
L
Zϕ
dϕ0 r2 (ϕ0 )
ϕ0
d.h. t = t(ϕ) → Umkehrfunktion ϕ = ϕ(t). Damit r = r[ϕ(t)], d.h. ~r = ~r(t) zugänglich!
Problem im Prinzip gelöst.
Keplersche Gesetze
Wenden wir diese Ergebnisse auf die Planetenbewegung an, erhalten wir eine Ellipse.
b2
. . . Scheitelkrümmungsradius
a
√
a2 − b2
=
. . . numerische Exzentrizität
a
p
e = a2 − b2 . . . lineare Exzentrizität
k=
a2 − b2
b2
damit (1 − )a = 1 −
a
=
=k
a2
a
k
k
⇒a=
=
= − γmM
2E = a
2Ek
1 − 2
1 − 1 − γmM
2
73
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
⇒ Für gegebene Massen ist die große Halbachse nur durch die Energie bestimmt!
b2 = a · k = −
γmM
L2
L2
·
=
−
2E
γm2 M
2mE
d.h. b =
√ L
−2mE
⇒ Die kleine Halbachse ist durch Drehimpuls und Energie bestimmt
A
z}|{
πab
dA
L
=
=
T
dt
2m
(Flächensatz, 2.2.4)
T . . . Periodendauer, Umlaufzeit
T =
3
3 √
2πm · γmM · L
2mπab
√
=
= πγm 2 M (−E)− 2 / 2
L
−L · 2E · −2mE
⇒ Bei gegebenen Massen ist die Periodendauer nur durch die Energie bestimmt.
Die große Halbachse ist ebenfalls durch die Energie festgelegt, damit
3
πγm 2 M
√
T =
2
2a
γmM
⇒ T2 =
3
r
2
= 2π
1 3
a2
γM
4π 2 3
a
γM
D.h. für zwei Planeten (m1 und m2 ), die um die Sonne (M ) umlaufen, gilt
T1
T2
2
=
74
a1
a2
3
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit wurden die Keplerschen Gesetze abgeleitet:
1. Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.
2. Der Fahrstrahl Sonne-Planet überstreicht in gleichen Zeiten gleiche Flächen.
3.
Ti
Tj
2
=
3
ai
aj
Die historische Reihenfolge ist umgekehrt:
Keplersche Gesetze empirisch gefunden (Astronomie)
↓
Gravitationsgesetz (Newton); allgemeiner, höhere Stufe der Erkenntnis
Wir skizzieren die historische Ableitung:
Kepler (2.) ⇒ Drehimpulserhaltung
⇒ Die Kraft ist eine Zentralkraft, sie hat nur eine radiale Komponente, d.h.
F~ = Fr e~r mit Fr = m(r̈ − rϕ̇2 ) (vgl. 1.2)
L = mr2 ϕ̇ = const.
Kepler (1.) ⇒ Ellipsengleichung
1
1
= (1 + cos ϕ)
r
k
d
dt
d
dt
1
ṙ
L
= − 2 = − ϕ̇ sin ϕ = −
sin ϕ
↑
r
r
k
kmr2
ϕ̇ =
L
mr 2
L
sin ϕ
km
L
L2
d.h. r̈ =
ϕ̇ cos ϕ =
cos ϕ (∗)
↑ km2 r 2
km
⇒ ṙ =
ϕ̇ =
75
L
mr 2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit in Fr = m(r̈ − rϕ̇2 )
↑
(∗) Fr = m
L2
L2
cos
ϕ
−
km2 r2
m2 r3
L2
=
mr2
↑
L
mr 2
2
L2
1
=−
(∗∗)
cos ϕ −
k
r
kmr2
|
{z
}
− k1
Kepler (2.)
dA
L
= const. =
dt
2m
|{z}
πab
T
⇒ π 2 a2 b2 =
⇔
L2 2
T
4m2
2 2
2
T2
2m b
2m k
=
4π
=
4π
a3
L2 a 2 ↑
L2
b = ka
Kepler (3.)
Ti2
a3i
= const. für alle Planeten i
⇒
L2
:= σ = const.,
m2 k
kann nur noch von Sonnenmasse abhängen
damit in (∗∗) Fr = −
L2
σm
=− 2
kmr2
r
3. Newtonsches Axiom: Fr ∼ M ⇒ σ = γM
Fr = −γ
mM
r2
Das Gravitationsgesetz ist aus der Planentenbeobachtung abgeleitet!
76
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Kosmische Geschwindigkeiten
Wir wollen einen Satelliten in die Umlaufbahn bringen, ausgehend von einem Punkt mit
Abstand R vom Erdmittelpunkt. Die Umlaufbahn r(t) soll außerhalb der Entfernung R
liegen.
d.h. R ≤ rmin =
↑
k
L2
=
2 M (1 + )
1 + ↑ γm
2
vorhin
k=
L
γm2 M
⇒ L2 = m2 R4 ϕ̇2 = m2 R2 vϕ2 ≥ γm2 M R(1 + )
⇒ vϕ2 ≥ (1 + )
Für einen Kreis, d.h. = 0 gilt vϕ2 ≥
γM
R
γM
R
Andererseits soll die Bewegung finit sein, d.h.
E<0
⇒ v2 <
k
1
mv 2
2
−
k
γmM
R
2 + v2
vϕ
r
77
2γM
R
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
graphische Veranschaulichung:
r
γM
km
= 7, 9
R
s
r E
2γM
km
=
= 11, 2
RE
s
R = RE ⇒ 1. kosmische Geschwindigkeit vI =
2. kosmische Geschwindigkeit vII
78
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.3 Dynamik eines MP-Systems
2.3.1 Bewegungsgleichungen
Wir betrachten N diskrete Körper, approximiert als frei bewegliche Massenpunkte.
Bewegungsgleichungen des MP-Systems
mν r~¨ν = F~ν
(ν = 1, 2, . . . , N )
Wir klassifizieren die Kräfte auf die Massenpunkte in
• äußere Kräfte, stammen von außerhalb des MP-Systems
• innere Kräfte, wirken zwischen den MP des Systems
(ext)
F~
| ν{z }
F~ν =
N
X
+
F~νµ
µ=1
µ6=ν
Resultante aller
äußeren Kräfte
auf MP ν
| {z }
Kraft vom MP µ auf
MP ν innerhalb des
Systems
3. Newtonsches Axiom ⇒ F~νµ = −F~µν
damit Bewegungsgleichungen
(ext)
mν r~¨ν = F~ν
+
N
X
F~νµ
µ=1
µ6=ν
Annahme: innere Kräfte sind Zentralkräfte
r~ − r~µ
F~
νµ = ± ν
~ |r~ν − r~µ |
Fνµ (plausibel für punktförmige Körper)
79
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.3.2 Impulsbilanz
Wir summieren über die Bewegungsgleichungen
N
X
mν r~¨ν =
ν=1
N
X
(ext)
F~ν
+
ν=1
N X
N
X
ν=1
N
X
F~νµ =
(ext)
F~ν
ν=1
µ=1
µ6=ν
{z
|
=0
}
(F~νµ =−F~µν )
Mit dem Gesamtimpuls des Systems
p~ =
N
X
p~ν =
ν=1
N
X
mν r~˙ν
ν=1
und der Resultante aller äußeren Kräfte
F~ (ext) =
N
X
(ext)
F~ν
ν=1
Impulsbilanz des Gesamtsystems
d~
p
= F~ (ext)
dt
Die zeitliche Änderung des Gesamtimpulses eines MP-Systems ist gleich der Resultante
der äußeren Kräfte.
(ext)
abgeschlossenes System ⇔ F~ν
= 0 ⇒ F~ (ext) = 0 ⇒
d~
p
dt
= 0, d.h. p~ = const.
Für ein abgeschlossenes System gilt die Erhaltung des Gesamtimpulses.
Wir definieren den Massenmittelpunkt:
N
r~c =
1 X
mν r~ν
m
mit m =
ν=1
N
X
ν=1
80
mν
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Offensichtlich gilt
p~ =
N
X
mν r~˙ν = mr~˙c
ν=1
d.h. mr~¨c = F~ (ext)
Der Massenmittelpunkt bewegt sich so, als ob in ihm die gesamte Masse des Systems
vereinigt wäre und an ihm die Resultante aller äußeren Kräfte wirkte.
d~
p
∧
F~ (ext) = 0 ⇒
= 0 = r~¨c = 0 ⇒ r~˙c = const.
dt
Bei fehlender äußeren Kraft ruht der Massenmittelpunkt des Systems oder vollführt eine
gleichförmig geradlinige Bewegung.
Bemerkungen:
• Die Bewegungsgleichung für den Massenmittelpunkt ist die nachträgliche Rechtfertigung für das Modell des Massenpunktes.
• Innere Kräfte spielen keine Rolle für die Bewegung des Massenmittelpunktes. Beispiel: explodierendes Geschoß; der Massenmittelpunkt der Splitter setzt die Flugbahn fort.
• Der Massenmittelpunkt wird oft als Schwerpunkt bezeichnet:
Wenn sich die Massenpunkte im homogenen Schwerefeld der Erde befinden, gilt
F~ (ext) =
k
mr~¨c
N
X
mν ~g = m~g ⇒ r~¨c = ~g
ν=1
D.h. der Massenmittelpunkt (oder Schwerpunkt) bewegt sich wie ein Massenpunkt
der Masse m unter dem Einfluß der Erdbeschleunigung ~g .
81
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
• Für Körper mit kontinuierlicher Masseverteilung kommt es zum Grenzübergang
von der Summation zur Integration:
Z
1
1 X
r~ν ∆mν → r~c =
~rdm
r~c =
m ν
m
Z
X
∆mν → m = dm
m=
ν
Falls ρ(~r) die Massendichte des Körpers ist, gilt:
dm = ρd3~r, damit folgt
R 3
R
1
r~c = m
d ~r ρ(~r)~r mit m = d3~r ρ(~r)
2.3.3 Energiebilanz
Bewegungsgleichung für den ν-ten Massenpunkt
mν r~¨ν = F~ν | · r~˙ν
d
dt
1 ˙ ˙
mr~ν · r~ν = r~˙ν · F~ν
| {z }
2
{z
}
|
Pν
Tν
Tν . . . kinetische Energie des ν-ten Massenpunkts
Pν . . . am ν-ten Massenpunkt umgesetzte Leistung
Durch Summation über ν erhalten wir:
dT
= P (∗)
dt
Die zeitliche Änderung der kinetischen Energie des Massenpunktsystems ist gleich der
Gesamtleistung.
82
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
mit der kinetischen Energie des Gesamtsystems
T =
N
X
Tν =
ν=1
N
X
1
ν=1
2
mν|r~˙ν |2
und der am Gesamtsystem erbrachten Leistung
P =
N
X
Pν =
ν=1
N
X
r~˙ν · F~ν
ν=1
F~ν , ν = 1, 2, . . . , N seien konservative Kräfte, d.h.
~ ν × F~ν = 0.
F~ν = F~ν (r~1 , r~2 , . . . , r~N ) ≡ F~ν (r~µ ) und ∇
~ νU.
Dann existiert ein Potential U = U (r~1 , r~2 , . . . , r~N ) ≡ U (r~µ ), so daß F~ν = −∇
Damit ergibt sich für die Gesamtleistung
P =
N
X
ν=1
Pν =
N
X
ν=1
F~ν · r~˙ν = −
N
X
~ ν U · r~˙ν = −
∇
ν=1
N X
X
dU
∂U dxiν
·
=−
i
∂xν dt
dt
ν=1
i
Damit wird aus der Bilanzgleichung (∗)
d
(T + U ) = 0
dt
Für konservative Systeme gilt die Erhaltung der Gesamtenergie
T + U = E = const.
Im Allgemeinen unterliegt ein Massenpunkt konservativen und dissipativen Kräften
(cons)
(diss)
F~ν = F~ν
(r~µ ) + F~ν
(r~µ , r~˙µ , t)
83
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Dann nimmt die mechanische Energiebilanz die Form
d
(T + U ) = P (diss)
dt
an, wobei
P (diss) =
N
X
(diss)
F~ν
· r~˙ν
ν=1
die Gesamtleistung der dissipativen Kräfte ist.
Erinnerung 2.3.1: Kräfte auf Massenpunkte können in innere und äußere Kräfte klassifiziert werden, innere Kräfte sind Zentralkräfte.
Oft hängen die inneren Kräfte nur vom gegenseitigen Abstand ab
~
rνµ
F~νµ = fνµ (rνµ ) rνµ
mit ~rνµ = r~ν − r~µ ,
rνµ = |~rνµ |
Dann haben die inneren Kräfte ein Potential
Uνµ
Zrνµ
= Uνµ (rνµ ) = −
drfνµ (r) = Uµν (rµν )
↑
∞
fνµ (r) = fµν (r)
~ ν Uνµ (rνµ )
F~νµ = −∇
~ µ Uνµ (rνµ )
=∇
~ µ Uµν (rµν ) = −F~µν
=∇
Das Gesamtpotential der inneren Kräfte lautet dann
U (int) =
N
1 X
Uνµ (rνµ )
2 ν,µ=1
ν6=µ
84
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beweis: Wir berechnen die Kraft auf den Massenpunkt ν
~ ν U (int) = −
−∇
=−
N
N
µ=1
µ=1
1X~
1X~
∇ν Uνµ (rνµ ) −
∇ν Uµν (rµν )
2
2
| {z }
N
X
~ ν Uνµ (rνµ ) =
∇
N
X
µ=1
Uνµ (rνµ )
F~νµ
µ=1
µ6=ν
Sind die äußeren Kräfte konservativ
(ext)
(ext)
~ ν Uν (r~ν )
F~ν
= F~ν
(rν ) = −∇
so existiert ein Gesamtpotential der äußeren Kräfte
U (ext) =
N
X
Uν (r~ν )
ν=1
Damit ist das Gesamtpotential
N
N
X
1 X
U=
Uνµ (rνµ ) +
Uν (r~ν )
2 ν,µ=1
ν=1
ν6=µ
Bemerkung: Für abgeschlossene Systeme gibt es nur innere Kräfte, die in der Regel als
konservativ angesehen werden können. Für abgeschlossene Systeme gilt also
erfahrungsgemäß der Energieerhaltungssatz.
85
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
2.3.4 Virialsatz
Bewegungen in Massenpunktsystemen sind ständig mit einer Umwandlung zwischen kinetischer und potentieller Energie verbunden. Wie groß sind im zeitlichen Mittel die
Beiträge von kinetischer und potentieller Energie zur Gesamtenergie?
Bewegungsgleichung für einen Massenpunkt:
mν r~¨ν = F~ν | · r~ν
mν r~ν · r~¨ν = F~ν · r~ν
d
(mν r~ν · r~˙ν ) − mν |r~˙ν |2 = r~ν · F~ν |Σ
dt
N
N
N
X
X
X
d
2
˙
˙
(mν r~ν · r~ν ) −
mν |r~ν | =
r~ν · F~ν
dt
ν=1
ν=1
ν=1
Die Kräfte sollen ein Potential besitzen
~ νU
r~ν · F~ν = −r~ν · ∇
N
N
N
X
X
X
d
2
˙
˙
~ νU
mν |r~ν | = −
r~ν · ∇
(mν r~ν · r~ν ) −
damit
dt
ν=1
ν=1
ν=1
Wir definieren den zeitlichen Mittelwert einer Funktion f (t) als
1
hf (t)i = lim
T →∞ T
t+ T2
Z
dt0 f (t0 )
t− T2
Wir mitteln jetzt obige Gleichung
*N
+
+ *N
X d
X
2
(mν r~ν · r~˙ν ) =
mν |r~˙ν | −
dt
ν=1
ν=1
|
{z
} |
{z
}
=0 (s.u.)
2hT i
86
*N
X
+
~ νU
r~ν · ∇
ν=1
|
{z
}
Virial des MP-Systems
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
*N
+
X d
1
˙
(mν r~ν · r~ν ) = lim
T →∞ T
dt
ν=1
N
X
mν r~ν · r~˙ν
t− 2
ν=1
|
t+ T
2
T
{z
}
endlich für fin. Bew.
⇒ hT i =
*N
1 X
2
+
~ νU
r~ν · ∇
ν=1
Der zeitliche Mittelwert der kinetischen Energie ist gleich dem halben Virial des MPSystems.
Oft hängt das Potential homogen von den Auslenkungen ab. Dann ist eine weitere Vereinfachung möglich.
Einschub: Eine Funktion mehrerer Variablen mit der Eigenschaft
f (λx1 , . . . , λxN ) = λm f (x1 , . . . , xN )
heißt homogene Funktion m-ten Grades. Für solche Funktionen gilt
N
X
i=1
xi
∂f
= mf
∂xi
(Satz von Euler)
Beweis:
N
X
d
∂f
| ⇒
(λx1 , . . . , λxN ) = mλm−1 f (x1 , . . . , xN )
xi
dλ
∂xi
i=1
speziell λ = 1
Anwendung im Falle z.B. des harmonischen Oszillators: Jetzt ist die potentielle Energie
eine homogene Funktion zweiten Grades in den {r~ν }, und entsprechend gilt
N
X
~ ν U = 2U
r~ν · ∇
ν=1
87
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
d.h. der Virialsatz nimmt die Form
hT i = hU i
an. In diesem Fall stimmen die Zeitmittel von potentieller und kinetischer Energie überein!
Bem.: Für Probleme der Himmelsmechanik ist das Gravitationspotential relevant, es ist
homogen vom Grad −1, entsprechend gilt 2 hT i = − hU i. Der Virialsatz erlaubt es, recht
gute Abschätzungen für die Gesamtmassen dynamisch gebundener Systeme wie Sternhaufen oder Galaxienhaufen zu finden. Die Gesamtmasse eines solchen Haufens kann
dann vollständig durch Beobachtungsgrößen wie Radialgeschwindigkeiten der Einzelobjekte ausgedrückt werden.
2.3.5 Drehimpulsbilanz
Bewegungsgleichung für den ν-ten Massenpunkt:
mν r~¨ν = F~ν |r~ν ×
mν r~ν × r~¨ν = r~ν × F~ν
| {z }
~ν
M
mit r~˙ν × r~˙ν = 0 gilt
d mν r~ν × r~¨ν =
mν r~ν × r~˙ν
dt |
{z
}
=r~ν ×p~ν =L~ν
88
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit
X
dL~ν
~ν |
=M
dt
ν
N
X
dL~ν
dt
ν=1
=
N
X
~ν
M
ν=1
~
dL
~
=M
dt
mit Gesamtdrehimpuls
X
~ =
L
L~ν =
X
ν
r~ν × p~ν
ν
und Gesamtdrehmoment
~ =
M
X
~ν =
M
ν
X
r~ν × F~ν =
X
ν
r~ν ×
F~ν
(ext)
ν
!
+
X
µ
Es gilt
X
ν,µ
1 X
r~ν × F~νµ =
r~ν × F~νµ + r~µ × F~µν
2 ν,µ
1 X
=
r~ν × F~νµ − r~µ × F~νµ
↑ 2
ν,µ
3. NA
=
1X
(r~ν − r~µ ) × F~νµ
2 ν,µ
Die inneren Kräfte sind Zentralkräfte, d.h.
F~µν
r~ν − r~µ
∼
~
|r~ν − r~µ |
|Fµν |
damit
X
(r~ν − r~µ ) × F~νµ = 0
ν,µ
~ =
d.h. M
N
X
(ext)
~ (ext)
r~ν × F~ν
=M
ν=1
89
F~νµ
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit ergibt sich die Drehimpulsbilanz
~
dL
~ (ext)
=M
dt
Die zeitliche Änderung des Gesamtdrehimpulses eines MP-Systems ist gleich dem Gesamtdrehmoment der äußeren Kräfte, wenn die inneren Kräfte Zentralkräfte sind (praktisch immer erfüllt).
~
~ (ext) = 0 ⇒ dL = 0 ⇒ L
~ = const.
M
dt
D.h. für abgeschlossene Systeme gilt die Drehimpulserhaltung.
Drehung um eine feste Achse
Ohne Beschränkung der Allgemeinheit betrachten wir eine Drehung um die z-Achse.
Lz =
X
mν (xν ẏν − yν ẋν )
kartesische Koord.
ν
=
X
↑
vgl.
mν ρ2ν ϕ̇ν
Zylinderkoord.
ν
2.2.4
Für Mz = 0 gilt Lz = const..
Falls die Massenpunkte untereinander starr verbunden sind (starrer Körper), besitzen
alle Massenpunkte die gleiche Winkelgeschwindigkeit
ϕ̇ν = ϕ̇ = ω ∀ν
90
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit Lz = ω
X
mν ρ2ν
ν
|
{z
}
θ
Lz = θω
θ . . . Trägheitsmoment des Systems bezüglich der z-Achse
Grenzübergang für einen ausgedehnten Körper mit kontinuierlicher Massenverteilung:
θ=
X
mν ρ2ν →
Z
dm · ρ2 =
Z
d3~r n(~r)ρ2
ν
mit Massendichte n(~r) =
dm(~
r)
dV
Bei konstantem Lz kann die Winkelgeschwindigkeit durch Änderung von θ variiert werden
(Bsp. Eiskunstlauf).
Rolle des Bezugspunkts
Der Drehimpuls hängt von der Wahl des Bezugspunkts ab. O und O0 seien zwei Bezugspunkte.
r~ν = r~0 + r~ν0
Sei r~˙0 = 0
91
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
~0 =
L
X
=
X
=
X
mν r~ν0 × r~˙ν
ν
mν (r~ν − r~0 ) × r~˙ν
ν
mν r~ν × r~˙ν − r~0 ×
X
mν r~˙ν
ν
ν
|
{z
}
mr~˙c =~
p (2.3.2)
~0 = L
~ − r~0 × p~
d.h. L
Der Drehimpuls ist also von der Wahl des ruhenden Bezugspunkts O0 dann unabhängig,
wenn der Massenmittelpunkt ruht (~
p = 0).
Jetzt bewege sich O0 bzgl. O, r~0 = r~0 (t).
~0 =
L
X
=
X
mν (r~ν − r~0 ) × (r~˙ν − r~˙0 )
ν
mν r~ν × r~˙ν −
ν
X
mν r~0 × r~˙ν −
ν
X
mν r~ν × r~˙0 +
X
ν
mν r~0 × r~˙0
ν
~ − r~0 × p~ − m(~
=L
rc − r~0 ) × r~˙0
woraus
~0
~
dL
d~
p
dL
=
− r~˙0 × p~ − r~0 ×
−m(r~˙c − r~˙0 ) × r~˙0 −m(~
rc − r~0 ) × r~¨0
{z
}
dt
dt
dt |
−~
p×r~˙0 , da r~˙0 ×r~˙0 =0
d.h.
~0
~
dL
dL
d~
p
=
− r~0 ×
− m(~
rc − r~0 ) × r~¨0
dt
dt
dt
Für das Gesamtdrehmoment gilt andererseits
~0 =M
~ 0 (ext) =
M
X
ν
(ext)
r~ν0 × F~ν
=
X
(r~ν − r~0 ) × F~ν
ν
92
(ext)
~ (ext) − r~0 ×
=M
d~
p
dt
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit
~0
~
dL
d~
p
dL
=
− r~0 ×
−m(~
rc − r~0 ) × r~¨0
dt
dt
dt
k
~ (ext)
M
|
{z
~ 0 (ext)
M
}
~0
dL
~ 0 (ext) − m(~
=M
rc − r~0 ) × r~¨0
dt
d.h.
~0
dL
dt
~0
=M
(ext)
gilt für
• r~¨0 = 0, d.h. O0 ruht oder bewegt sich gleichförmig
• r~c (t) = r~0 (t), d.h. O0 ist der Massenmittelpunkt
2.3.6 Spezielle Probleme
A) Zweikörperproblem
Bewegungsgleichungen
m1 r~¨1 = −f (r21 )
m2 r~¨2 = f (r21 )
Transformation auf Massenmittelpunktsvektor und Abstandsvektor
m1 r~1 + m2 r~2
= r~c
m1 + m2
m2 r~1 − m2 r~2
m2
r~10 = r~1 − r~c =
=−
~r21
m1 + m2
m1 + m2
m1 r~2 − m1 r~1
m1
r~20 = r~2 − r~c =
=
~r21
m1 + m2
m1 + m2
93
~r21
(∗)
r21
~r21
(∗∗)
r21
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
−(∗) · m2 + (∗∗) · m1
n
o
~
r21
⇒ m1 m2 (r~¨2 − r~¨1 ) = f (r21 ) m2 ~rr21
+
m
1
r21
21
| {z }
~
r¨21
⇒
m1 m2 ¨
~r21 = f (r21 ) ~rr21
21
m1 + m2
| {z }
µ...reduzierte Masse
Damit ist das Zweikörperproblem auf ein Einkörperproblem reduziert, die Bewegung der
beiden Massen relativ zueinander ist äquivalent zur Bewegung eines Massenpunktes mit
Masse µ im konservativen Zentralfeld f (r) ~rr .
Aus ~r21 (t) und dem Massenmittelpunkt r~c können dann r~1 (t) und r~2 (t) bestimmt werden.
Wegen der Impulserhaltung gilt für den Massenmittelpunkt
r~¨c = 0 ⇒ r~c (t) = c1 t + c2
(gleichförmig geradlinig bewegt oder in Ruhe)
Bemerkung: Das Kepler-Problem ist eigentlich ein Zweikörperproblem, da die Sonne nicht
raumfest ist. Sowohl die Sonne als auch die Erde bewegen sich auf Ellipsen.
Die Ellipse der Sonne / Erde ist
m
m
≈
kleiner
M +m
M
/
M
≈ 1 größer
M +m
als die in 2.2.6 berechnete Ellipse. Die Sonnenmasse beträgt etwa das 330’000
94
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
fache der Erdmasse, so daß die Korrektur klein ist. Anders sieht es beim
Mond aus, dessen Masse ist immerhin 1/80 der Erdmasse.
B)Raketengleichung
Besonderheit bei einer Rakete: Es handelt sich um die Bewegung eines Körpers mit
veränderlicher Masse.
∧
Rakete + ausgestoßene Masse = MP-System
↑
Massenerhaltung
Bilanzgleichung für den Gesamtimpuls:
p~˙ = F~ (ext)
Impuls zur Zeit t: p~ = m~v
Impuls zur Zeit t + ∆t:
p~ + ∆~
p = [m + ∆m][~v + ∆~v ] + [−∆m][~v + ∆~v + ~u] = |{z}
m~v +m∆~v − ∆m~u
p
~
95
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
∆~
p = m∆~v − ∆m~u
|·
1
, lim
∆t ∆t→0
p~˙ = m~v˙ − ṁ~u
k
~ (ext)
F
⇒ Raketengleichung
m~v˙ = F~ (ext) + ṁ~u
⇒ Impulsbilanz für Rakete
d
(m~v ) = F~ (ext) + ṁ(~v + ~u)
| {z }
dt
Schubkraft
Eine Änderung des Raketenimpulses erfolgt durch eine äußere Kraft und die Schubkraft.
Bsp.: geradliniger Aufstieg einer Rakete im homogenen Schwerefeld der Erde
~v = ż e~z
~u = −ue~z
F~ (ext) = −mg e~z
Damit ergibt sich die Raketengleichung
z̈ = −g − ṁ
mu
Rt 0 ṁ
⇒ ż = −g(t − t0 ) − dt m u
t0
z(t) = − 12 g(t − t0 )2 −
Rt
dt0
t0
mit ṁ < 0
Raketengeschw., ż(t0 ) = 0
Rt0
t0
ṁ
dt00 m
u
Bahnkurve
Speziell für u = const. folgt
m(t0 )
ż = −g(t − t0 ) + u ln
m(t)
96
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Ist für t = tf der Treibstoff verbraucht, hat die Rakete die Geschwindigkeit
m(t0 )
vf = −g(tf − t0 ) + u ln
m(tf )
und für t > tf unterliegt sie den Gesetzen des senkrechten Wurfes
ż = −g(t − tf ) + vf
u ln
h
m(t0 )
m(tf )
i
. . . Endgeschwindigkeit ohne äußere Kraft, hängt vom Massenverhältnis ab.
⇒ Bei festem Massenverhältnis ist die maximal erreichbare Geschwindigkeit umso größer,
je schneller die Masse ausströmt.
97
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
3 Lagrangesche Mechanik
3.1 Das d’Alembertsche Prinzip
3.1.1 Bedingungsgleichungen
Vom mechanischen Standpunkt kann man die Welt als Massenpunktsystem auffassen,
mit Kräften zwischen den MP. Das ist praktisch nicht durchführbar, da makroskopische
Systeme typischerweise ∼ 1023 Teilchen besitzen.
Wir versuchen daher, das Gesamtsystem näherungsweise als Objekt + Umgebung zu
beschreiben.
Beispiel: Körper, der eine schiefe Ebene hinabgleitet
Die Umgebung (der schiefen Ebene) kann durch eine Zwangskraft beschrieben werden,
die den Körper zwingt, sich ausschließlich auf der schiefen Ebene zu bewegen.
Der Körper kann sich nicht frei bewegen, sondern nur gebunden bzw. eingeschränkt.
Die Einschränkung der Bewegung kann in Form von Bedingungsgleichungen formuliert
werden. Im Fall der schiefen Ebene ist die Bedingungsgleichung
x(t) sin α − z(t) cos α = 0
Für komplexere Systeme aus mehreren (N ) Massenpunkten verwenden wir im Folgenden
die Notation von 3N kartesischen Koordinaten und 3N Kraftkomponenten. Ebenfalls
betrachten wir 3N Massen, wobei die Massen, die zu einem MP gehören, jeweils gleich
sind.
98
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit lauten die Newtonschen Bewegungsgleichungen:
mi ẍi = Fi
(i = 1, 2, . . . , 3N )
Bindungen zwischen den MP (innere Bindungen) bzw. Bindungen an feste Kurven oder
Flächen im Raum (äußere Bindungen) formulieren wir als Nebenbedingungen.
Wir unterscheiden 4 Typen von Nebenbedingungen
Holonome NB
lassen sich in Form von Gleichungen folgender Art formulieren:
fk (xj , t) = 0
(k = 1, 2, . . . , r)
[fk (xj , t) ≡ fk (x1 , x2 , . . . , x3N , t)]
bzw. in der Form
3N
X
∂fk
i=1
⇔
3N
X
∂fk
i=1
∂xi
∂xi
ẋi +
dxi +
∂fk
=0
∂t
∂fk
dt = 0
∂t
r . . . Anzahl der Nebenbedingungen, r ≤ 3N
f = 3N − r . . . Anzahl der Freiheitsgrade des Systems
Anholonome NB
lassen sich nur in Form von Differentialgleichungen formulieren
3N
X
fki (xj , t)ẋi + fk0 (xj , t) = 0
i=1
3N
X
fki (xj , t)dxi + fk0 (xj , t)dt = 0
i=1
99
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
wobei der obige Ausdruck kein vollständiges Differential ist, im Unterschied zu holonomen
Nebenbedingungen.
Beispiel: Bewegung eines Schlittschuhs auf der Eisfläche (x-y-Ebene)
Die Bewegung kann nur in Richtung der Schneide erfolgen, d.h.
ẏ − tan ϕẋ = 0
Die Bedingung ist anholonom, da sie nicht als vollständiges Differential von f (x, y, ϕ)
formulierbar ist.
dy − tan ϕdx + 0dϕ = 0
{z
}
|
6=df
Zu den anholonomen Bedingungen werden auch Bedingungen in Form von Ungleichungen
gezählt.
Beispiel: Massenpunkt, der in einem bestimmten Volumen gebunden ist:
(x − x0 )2 + (y − y0 )2 ≤ R2
100
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Skleronome NB
hängen nicht explizit von der Zeit ab, d.h. für holonome Bedingungen
∂fk
=0
∂t
und für anholonome Bedingungen
∂fki
=0
∂t
(i = 1, 2, . . . , 3N )
fk0 = 0
Rheonome NB
sind explizit zeitabhängige Bedingungen.
Für Systeme, die mehreren NB genügen, können diese unterschiedlicher Art sein, holonom, anholonom, teils skleronom, teils rheonom.
3.1.2 Das d’Alembertsche Prinzip
Ein System von N MP unterliege r Nebenbedingungen, z.b. holonom
3N
X
∂fk
i=1
∂xi
dxi +
∂fk
dt = 0
∂t
Diese Nebenbedingungen haben zur Folge, daß die Massenpunkte nicht nur den eingeprägten Kräften Fi ausgesetzt sind, sondern auch noch Zwangskräften F̃i , die die Bewegungsfreiheit der Massenpunkte einschränken. Damit ergeben sich modifizierte Bewegungsgleichungen
mi ẍi = Fi + F̃i
(i = 1, 2, . . . , 3N )
101
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wie können die Zwangskräfte durch die Nebenbedingungen ausgedrückt werden?
Wir betrachten zunächst virtuelle Verrückungen δxi (i = 1, 2, . . . , 3N ), d.h. infinitesimal
kleine Auslenkungen des Systems, die mit den Nebenbedingungen vereinbar sind und
momentan geschehen sollen, d.h. δt = 0.
D.h. für holonome Bedingungen
3N
X
∂fk
i=1
∂xi
dxi +
∂fk
dt = 0
∂t
sind virtuelle Verrückungen solche, die folgende Gleichung erfüllen:
3N
X
∂fk
i=1
∂xi
δxi = 0
Analog gilt für virtuelle Verrückungen unter anholonomen Bedingungen
3N
X
fki δxi = 0
i=1
Für bilaterale Bindungen (d.h. Bindungen, die durch Gleichungen - im Unterschied zu
Ungleichungen - beschrieben werden) lautet das
d’Alembertsche Prinzip
3N
X
F̃i δxi = 0
i=1
Zwangskräfte leisten bei virtuellen Verrückungen keine Arbeit.
D.h. die Zwangskräfte stehen senkrecht auf den erlaubten Bewegungsrichtungen.
Hierbei handelt es sich um eine Erfahrungstatsache, es kann nicht bewiesen werden.
102
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Aus F̃i = mi ẍi − Fi folgt
3N
X
(mi ẍi − Fi )δxi = 0
i=1
Für unilaterale Bindungen, d.h. einseitige Bindungen, wo z.B. Massenpunkte auf ein
bestimmtes Volumen eingeschränkt sind, zeigt die Zwangskraft auf die Seite, in der die
Massenpunkte sich bewegen können.
D.h. dann gilt
3N
X
F̃i δxi ≥ 0 ⇔
3N
X
(mi ẍi − Fi )δxi ≥ 0
i=1
i=1
Im mechanischen Gleichgewicht sind die Massenpunkte in Ruhe, d.h. ẍi = 0 ∀i
Dann gilt das
Prinzip der virtuellen Arbeit
3N
X
Fi δxi ≤ 0
i=1
Ein MP-System ist dann und nur dann im Gleichgewicht, wenn die gesamte virtuelle
Arbeit der am System angreifenden eingeprägten Kräfte verschwindet bzw. nicht positiv
ist.
103
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beispiel: Hebel im Schwerefeld der Erde
Einzig mögliche virtuelle Verrückung ist eine kleine Drehung
virtuelle Arbeit F (a) aδϕ − F (b) bδϕ = 0
⇔ (F (a) a − F (b) b)δϕ = 0
↑
beliebig
⇒ Gleichgewichtsbedingung
F (a) a = F (b) b
(Hebelgesetz)
3.1.3 Bilanzgleichungen
Die Bilanzgleichungen für MP-Systeme aus 2.3.2, 2.3.3 und 2.3.5 bleiben natürlich gültig,
wenn alle wirkenden Kräfte, d.h. eingeprägte und Zwangskräfte berücksichtigt werden.
Wir können auch die Zwangskräfte in innere und äußere Zwangskräfte einteilen
N
X˜
˜
˜
F~ν = F~ν(ext) +
F~νµ
µ=1
Die Impulsbilanz lautet dann
d~
p
˜
= F~ (ext) + F~ (ext)
dt
104
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Entsprechend lautet die Drehimpulsbilanz
~
dL
~ (ext) + M
~˜ (ext)
=M
dt
Für die kinetische Energie gilt
dT
= P + P̃
dt
P + P̃ . . . Leistung aller am System angreifenden eingeprägten und Zwangskräfte
Wir betrachten speziell skleronome Bedingungen der Form
3N
X
fki dxi = 0
i=1
Dann gibt es keinen Unterschied zwischen virtuellen und realen Verrückungen
dxi = δxi
und das d’Alembertsche Prinzip lautet
3N
X
F̃i δxi =
3N
X
i=1
F̃i dxi = 0
i=1
Dann gilt für
P̃ =
3N
X
F̃i ẋi = 0
i=1
und die Bilanzgleichung für T geht in die Bilanzgleichung für freie Systeme über
dT
=P
dt
d.h. die mechanische Energiebilanz ist durch die eingeprägten Kräfte bestimmt.
105
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Falls diese ein Potential besitzen
Fi = −
∂U
∂xi
gilt wie für freie Systeme
d
∂U
(T + U ) =
dt
∂t
∂U
∂t
(vgl. 2.2.3)
= 0 für konservative Systeme
3.1.4 Spezielle Probleme
A) Massenpunkt auf schiefer Ebene
Ein Massenpunkt bewege sich reibungsfrei unter Einfluß der Schwerkraft
eingeprägte Kraft: F~ = −mg e~z
Nebenbedingung: z = x tan α bzw. δz = δx tan α
1 Teilchen, 1 Nebenbedingung → 3 − 1 = 2 Freiheitsgrade
106
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
d’Alembertsches Prinzip
3N
X
(mi ẍi − Fi )δxi = 0
i=1
→ mẍδx + mÿδy + (mz̈ + mg)δz = 0
k
δx tan α
⇒ [ẍ + (z̈ + g) tan α] δx + ÿδy = 0
δx und δy sind frei wählbar
⇒ ẍ + (z̈ + g) tan α = 0 (∗)
ÿ = 0
Die Bewegung in y ist geradlinig gleichförmig.
Es ergeben sich 2 Gleichungen, die zusammen mit der Nebenbedingung z = x tan α zu
lösen sind.
z̈ = ẍ tan α → (∗) ⇒ ẍ (1 + tan2 α) +g tan α = 0
{z
}
|
1
cos2 α
⇒ ẍ = −g sin α cos α
Die Bewegung in x ist gleichförmig beschleunigt. Für s =
s̈ = −g sin α = −
x
cos α
gilt
|F~k |
m
Die Bewegung längs der s-Achse erfolgt unter Einfluß der Projektion der Schwerkraft auf
diese Achse.
107
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
˜
Die Zwangskraft F~ = m~r¨ − F~ lautet in Komponenten
F˜x = mẍ = −mg sin α cos α = −|F~⊥ | sin α
F˜y = mÿ = 0
F˜z = mz̈ + mg = m(ẍ tan α + g) = −mg (sin2 α − 1) = |F~⊥ | cos α
|
{z
}
− cos2 α
˜
D.h. F~ = −F~⊥ , die Zwangskraft ist entgegengesetzt gleich der Komponente der Schwerkraft, die orthogonal zur schiefen Ebene wirkt.
B) Mathematisches Pendel
Ein Massenpunkt befindet sich an einer massenlosen, drehbar aufgehängten Stange.
Eingeprägte Kraft: F~ = mg e~x = mg cos ϕe~ρ − mg sin ϕe~ϕ
Nebenbedingungen: z = 0, ρ = l bzw. δz = 0, δρ = 0
1 Teilchen, 2 Nebenbedingungen → 3 − 2 = 1 Freiheitsgrad
108
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
virtuelle Verrückung
δ~r = δρe~ρ + ρδϕe~ϕ + δz e~z = ρδϕe~ϕ
k
k
0
0
d’Alembertsches Prinzip:
0 = (m~r¨ − F~ ) · δ~r = (m~r¨ · e~ϕ − F~ · e~ϕ )ρδϕ = m(ρϕ̈ + 2ρ̇ϕ̇ + g sin ϕ)ρδϕ
↑
~
r¨ in Zylinderkoord. (1.2)
Da δϕ frei wählbar ist, folgt
ρϕ̈ + 2ρ̇ϕ̇ = −g sin ϕ
Diese Gleichung ist zusammen mit den Nebenbedingungen zu lösen: ρ = l, d.h. ρ̇ = 0
g
⇒ ϕ̈ = − sin ϕ
l
Für kleine Auslenkungen (ϕ 1) gilt sin ϕ ≈ ϕ
Damit ergibt sich die Bewegungsgleichung für eine harmonische Schwingung (vgl. 1.4)
ϕ̈ + ω 2 ϕ = 0
mit ω =
⇒T =
q
2π
ω
g
l
= 2π
q
l
g
Z.B. erfolgt die Eichung von Pendeluhren über die Pendellänge.
109
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Jetzt betrachten wir beliebige Auslenkungen
Wir nutzen die Energieerhaltung bei skleronomen Bedingungen aus:
T + U = E = const.
T = 21 m|~r˙ |2 = 21 m(ρ̇2 + ρ2 ϕ̇2 + ż 2 ) = 12 ml2 ϕ̇2
k
k
0
0
U = −mgρ cos ϕ = −mgl cos ϕ
1
⇒ E = ml2 ϕ̇2 − mgl cos ϕ
2
1
E
g
= ϕ̇2 − cos ϕ
2
ml
2
l
|{z}
=:
k
ω2
1
= ϕ̇2 − ω 2 cos ϕ
2
dϕ
dt
2
= 2( + ω 2 cos ϕ)
Z
dϕ
p
t=
+ const.
2( + ω 2 cos ϕ)
Wir betrachten U (ϕ) = −ω 2 cos ϕ
110
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Bewegung ist finit für −ω 2 < < ω 2 . Die Umkehrpunkte (ϕ̇ = 0) folgen aus
U (ϕ0 ) = −ω 2 cos ϕ0 = Wir integrieren für eine finite Bewegung mit den Anfangsbedingungen
ωt =
t = 0, ϕ = 0
Rϕ
dϕ0
q
0
2(cos ϕ0 −cos ϕ0 )
| {z }
− 2
ω
Wir integrieren numerisch bis ϕ = ϕ0 , dann offensichtlich t =
T
4
s ϕ20
l
⇒ T ≈ 2π
1+
+ ...
g
16
Für ϕ0 → 0 ergibt sich wieder ein harmonischer Oszillator, für ϕ0 > 0 hängt die Schwingungsdauer auch von der Amplitude ϕ0 ab.
˜
Die Zwangskraft F~ = m~r¨ − F~ lautet in Komponenten
F˜ρ = m(ρ̈ − ρϕ̇2 ) −Fρ = −ml(ϕ̇2 + ω 2 cos ϕ)
{z
} k
|
−mlϕ̇2
mg cos ϕ
F˜ϕ = m(ρϕ̈ + 2ρ̇ϕ̇) −Fϕ = ml (ϕ̈ + ω 2 sin ϕ) = 0
|
{z
} k
{z
}
|
mlϕ̈
−mg sin ϕ
=0 (Bewegungsgl.)
F˜z = mz̈ − Fz = 0
k
0
k
0
D.h. die Zwangskraft hat nur eine Komponente
˜
F~ = −ml(ϕ̇2 + ω 2 cos ϕ)e~ρ
Diese muß die ρ-Komponente der Schwerkraft kompensieren und die Radialkraft realisieren, die die Kreisbewegung erzwingt.
111
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
3.1.5 Starrer Körper
Ein starrer Körper entspricht einem System von Massenpunkten mν , deren Abstände
sich nicht ändern sollen.
Die festen Abstände reduzieren die Freiheitsgrade des Systems auf typischerweise 6:
Drehachse
d’Alembertsches Prinzip:
N
X
(mν r~¨ν − F~ν )δ r~ν = 0
ν=1
Nebenbedingungen:
r~ν = r~1 + r~ν 0
δ r~ν = δ r~1 + δ r~ν 0
wobei δ|r~ν 0 | = 0
wobei m1 ein willkürlich herausgegriffener Massenpunkt ist.
112
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Für einen festen Abstand δ|r~ν 0 | = 0 kann der Massenpunkt mν nur eine Drehung um
eine Achse durch den Massenpunkt m1 ausführen:
δ r~ν 0 = δ ϕ~ν × r~ν 0 (vergleiche Drehung um eine Achse in 2.1.5)
damit δ r~ν = δ r~1 + δ ϕ~ν × r~ν 0
Bei einem starren Körper müssen bei einer Drehung alle Winkel gleich sein, d.h.
δ ϕ~ν = δ ϕ
~
damit δ r~ν = δ r~1 + δ ϕ
~ × r~ν 0
⇒ r~˙ν = r~˙1 + ω
~ × r~ν 0
Die beliebig wählbaren δ r~1 und δ ϕ
~ sind die 6 Freiheitsgrade des starren Körpers
(3 Translationen, 3 Rotationen).
Jetzt mit δ r~ν ins d’Alembertsche Prinzip:
N
N
X
X
¨
~
⇒ δ r~1 ·
(mν r~ν − Fν ) + δ ϕ
~×
r~ν 0 · (mν r~¨ν − F~ν ) = 0
ν=1
ν=1
|
δϕ
~·
N
P
{z
(mν r~ν 0 ×r~¨ν −r~ν 0 ×F~ν )
ν=1
113
}
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Anmerkung: Für das Spatprodukt gilt
(~a × ~b) · ~c = (~b × ~c) · ~a = (~c × ~a) · ~b
Beweis über Komponentendarstellung
(~a × ~b)i = εijk aj bk
(Summenkonvention)
wobei für das Permutationssymbol gilt
εijk =




+1 (i, j, k) gerade Permutation von 1, 2, 3




−1 (i, j, k) ungerade Permutation von 1, 2, 3






0 mindestens zwei Indizes gleich
Wichtige Rechenregel
εijk εimn = δjm δkn − δjn δkm
εijk εijn = 2δkn
εijk εijk = 6
(Summenkonvention)
Wegen r~ν 0 = r~ν − r~1 folgt weiters
δ r~1 ·
N
X
ν=1
(mν r~¨ν − F~ν ) + δ ϕ
~·
N h
X
i
mν r~ν × r~¨ν − r~ν × F~ν − r~1 × (mν r~¨ν − F~ν ) = 0
ν=1
114
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Da δ r~1 und δ ϕ
~ frei wählbar sind, folgt:
N
X
mν r~¨ν =
ν=1
N
X
mν r~ν × r~¨ν =
ν=1
N
X
ν=1
N
X
F~ν
r~ν × F~ν
ν=1
Das entspricht gerade der Impulsbilanz
d~
p
= F~ = F~ (ext)
dt
und der Drehimpulsbilanz
~
dL
~ =M
~ (ext)
=M
dt
Gesamtkraft und Gesamtdrehmoment sind nur durch die eingeprägten äußeren Kräfte
bestimmt, da die Zwangskräfte als innere Kräfte keinen Beitrag leisten.
Ist der starre Körper nicht frei beweglich, sondern durch Nebenbedingungen eingeschränkt, so treten noch äußere Zwangskräfte und Zwangsdrehmomente auf. Dann gilt
d~
p
˜
= F~ (ext) + F~ (ext) ;
dt
~
dL
~˜ (ext)
~ (ext) + M
=M
dt
115
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beispiel: Um feste Achse drehbarer Körper
o.B.d.A entspreche die Drehachse der z-Achse, r~1 fixiere einen Punkt auf der Achse.
Damit δ r~1 = 0, δ ϕ
~ = δϕe~z
und es gilt die Drehimpulsbilanz für die z-Komponente
dLz
= Mz = Mz(ext)
dt
(vgl. 2.3.5) Lz = θϕ̇
mit θ =
N
X
mν ρ2ν =
Z
dmρ2
ν=1
wobei θ das Trägheitsmoment des starren Körpers bezogen auf die Drehachse (z-Achse)
ist. ρ ist dabei der senkrechte Abstand des jeweiligen Massenpunktes von der Drehachse.
Damit lautet die Bewegungsgleichung
θϕ̈ = M
Für skleronome Bedingungen gehen in die Energiebilanz nur eingeprägte Kräfte ein. Falls
diese ein Potential besitzen gilt
d
∂U
(T + U ) =
dt
∂t
hier ist U = U (ϕ, t)
T =
N
X
1
ν=1
2
mν |r~˙ν |2 =
N
X
1
ν=1
2
2
mν (ρ˙ν +
ρ2ν ϕ˙ν 2
2
+ z˙ν ) =
k
k
k
0
ϕ̇2
0
116
N
X
1
ν=1
1
mν ρ2ν ϕ̇2 = θϕ̇2
2
2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit lautet die Energiebilanz
d 1 2
θϕ̇ + U (ϕ, t) =
dt 2
∂U
∂U
θϕ̇ϕ̈ +
ϕ̇ +
=
∂ϕ
∂t
∂
U (ϕ, t)
∂t
∂U
∂t
∂U
θϕ̈ = −
|{z}
∂ϕ
M
⇒M =−
∂U
∂ϕ
D.h. die Drehung eines starren Körpers um eine feste Achse ist analog zur eindimensionalen Translationsbewegung mit den Entsprechungen
x↔ϕ
Gilt die Energieerhaltung, d.h.
∂U
∂t
m↔θ
F ↔M
= 0, können wir die Bewegungsgleichung integrieren
Z
θϕ̈ = M → t =
dϕ
p
2[E − U (ϕ)]/θ
(analog zum Vorgehen in 2.2.5 mit den oben genannten Ersetzungen)
117
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Steinerscher Satz
Das Trägheitsmoment ist abhängig von der Wahl der Achse
θ=
=
N
X
ν=1
N
X
mν ρ2ν
=
N
X
2
0
0
mν (ρ02
ν + ρc − 2ρc ρν cos ϑν )
ν=1
2
mν ρ02
ν +mρc − 2ρc
ν=1
|
N
X
mν ρ0ν cos ϑ0ν
ν=1
{z
θc
}
|
{z
mxc =0
}
θ = θc + mρ2c
Ist das Trägheitsmoment bezüglich der durch den Massenmittelpunkt gehenden Achse
bekannt, so ist es (bei bekannter Gesamtmasse) bezüglich jeder dazu um ρc parallel
verschobenen Achse bekannt.
118
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Freie Achsen
Die Zwangskräfte und Zwangsdrehmomente sind gegeben durch
d~
p ~ (ext)
˜
F~ (ext) =
−F
dt
~
~˜ (ext) = dL − M
~ (ext)
M
dt
(wichtig für die Fixierung der Drehachsen)
Wir betrachten einen Körper, der im Schwerefeld der Erde um eine Achse, welche senkrecht auf der Erdoberfläche steht, rotiert. Dafür gilt:
˜
F~ (ext) = mr~¨c + mg e~z = −mρc ϕ̇2 e~ρ + mg e~z
↑
ρ̇ = 0 = ϕ̈
~˙ + mg r~c × e~z = (L˙x + mgyc )e~x + (L˙y − mgxc )e~y
~˜ (ext) = L
M
(Annahme: M̃z
(ext)
= 0, d.h. Lz ändert sich nicht)
˜
Die Zwangskraft F~ (ext) ist gerade die Kraft, die den Körper (Massenmittelpunkt) auf
eine Kreisbahn vom Radius ρc in fester Höhe über der Erdoberfläche zwingt.
~˜ (ext) ist das zur Achsenfixierung nötige Zwangsdrehmoment, wir betrachten die entM
sprechenden Drehimpulskomponenten:
Für eine Kreisbewegung gilt:


xν = ρν cos ϕ 
⇒

yν = ρν sin ϕ 
x˙ν = −ϕ̇yν
y˙ν = ϕ̇xν
x¨ν = −ϕ̈yν − ϕ̇y˙ν = −ϕ̇2 xν
k
0 gleichförmige Bewegung
y¨ν = ϕ̈xν + ϕ̇x˙ν = −ϕ̇2 yν
k
0
119
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
damit
N
N
N
ν=1
ν=1
X
X
d X
L˙x =
mν (yν z˙ν − zν y˙ν ) = −
mν zν y¨ν =
mν zν ϕ̇2 yν
dt
k
ν=1
0
N
N
N
ν=1
ν=1
X
X
d X
mν (zν x˙ν − xν z˙ν ) =
mν zν x¨ν = −
mν zν ϕ̇2 xν
L˙x =
dt
k
ν=1
0
mit dem
Deviationsmoment (auch „dynamische Unwucht“)
θij =
N
X
mν (xν )i (xν )j
i 6= j
ν=1
ergibt sich
L˙x = ϕ̇2 θyz
L˙y = −ϕ̇2 θxz
Anstelle zeitabhängige Deviationsmomente zu benutzen ist es oft sinnvoll, in ein körperfestes Koordinatensystem zu wechseln.
(x’ und y’ sind körperfest)
120
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
es gilt
xν = x0ν cos ϕ − yν0 sin ϕ
yν = x0ν sin ϕ + yν0 cos ϕ
zν = zν0
damit ergibt sich
θxz = θx0 z 0 cos ϕ − θy0 z 0 sin ϕ
θyz = θx0 z 0 sin ϕ + θy0 z 0 cos ϕ
wobei die körper- und achsenspezifischen Deviationsmomente θx0 z 0 und θy0 z 0 jetzt zeitunabhängig sind.
Verschwinden für eine gewählte, durch den Massenmittelpunkt des Körpers gehende
Drehachse die Deviationsmomente, so ist kein Zwangsdrehmoment notwendig, um ein
Kippen der Drehachse zu verhindern. Ein um eine solche Achse nach einem Anstoß in
Drehung versetzter Körper kann um diese Achse frei weiterrotieren, da die Achse ihre
Lage beibehält.
Eine solche Achse wird freie Achse genannt, bzw. Hauptträgheitsachse oder Hauptachse.
Hauptachsen verlaufen durch den Massenmittelpunkt und sind Symmetrieachsen.
121
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Physisches Pendel
Das physische Pendel entspricht einem starren Körper, der um eine Achse parallel zur
Erdoberfläche frei beweglich ist.
Die Bewegungsgleichung lautet
θϕ̈ = Mz = −yc Fx = −ρc sin ϕ · mg
⇒ ϕ̈ = −
ρc mg
sin ϕ
θ
analog zur Bewegungsgleichung des mathematischen Pendels (3.1.3):
g
ϕ̈ = − sin ϕ
l
Wir definieren eine reduzierte Pendellänge
l=
θ
ρc m
und können alle Ergebnisse aus 3.1.3 übertragen.
122
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Mit dem Steinerschen Satz
θ = θc + mρ2c
erhalten wir
θc
θc
l=
+ ρc = ρc 1 + 2
ρc m
ρc m
d.h. für ein festes l (bzw. für eine vorgegebene Schwingungsdauer) gibt es zwei mögliche
ρc , d.h. zwei mögliche Aufhängungspunkte.
D.h. speziell für die Wahl des Schwingungsmittelpunkts zum Aufhängungspunkt ergibt
sich die selbe Schwingungsdauer (Beweis: Übung).
Die minimale Pendellänge ergibt sich aus
dl
dρc
=0
⇒ − ρθ2cm + 1 = 0 ⇒ ρc =
q
c
diese gibt Anlaß zur kleinstmöglichen Schwingungsdauer.
123
θc
m
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
3.2 Lagrangesche Gleichungen
3.2.1 Lagrangesche Gleichungen 1. Art
Wir starten vom d’Alembertschen Prinzip
3N
X
(mi ẍi − Fi )δxi = 0
i=1
mit bilateralen, anholonomen Bedingungen
3N
X
fki dxi + fk0 dt = 0
(k = 1, 2, . . . , r)
i=1
(für holonome Bedingungen fki →
∂fk
∂xi ,
fk0 →
∂fk
∂t )
Wir multiplizieren die k-te Bedingung für dt = 0 mit λk und summieren über k:
r X
3N
X
λk fki δxi = 0
k=1 i=1
Wir subtrahieren das Ergebnis vom d’Alembertschen Prinzip
⇒
3N
X
mi ẍi − Fi −
i=1
r
X
!
λk fki
δxi = 0
k=1
Von 3N virtuellen Verrückungen δxi sind 3N − r = f frei wählbar, r sind durch Nebenbedingungen festgelegt.
Wir wählen die Lagrangeschen Multiplikatoren λk so, daß für die nicht frei wählbaren
δxi (i = 1, ..., r) die Vorfaktoren
mi ẍi − Fi −
r
X
k=1
124
!
λk fki
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
verschwinden (r Gleichungen für r Unbekannte λk ).
Für die verbleibenden f virtuellen Verrückungen δxi (i = r + 1, ..., 3N ) verschwinden
die Vorfaktoren automatisch, da diese frei wählbar sind, und die Gesamtsumme nach
Konstruktion verschwinden muß
Damit erhalten wir die
Lagrangeschen Gleichungen 1. Art
mi ẍi = Fi +
r
X
λk fki
i = 1, 2, . . . , 3N
k=1
(3N Gleichungen)
die zusammen mit den r Nebenbedingungen
3N
X
fki ẋi + fk0 = 0
k = 1, 2, . . . , r
i=1
zu lösen sind.
D.h. wir haben 3N + r Gleichungen zur Bestimmung von 3N Koordinaten xi und r
Lagrangeschen Multiplikatoren λk .
Aus den Lagrangeschen Gleichungen 1. Art liest man unmittelbar die
Zwangskräfte F̃i =
r
X
k=1
ab. Speziell für holonome Bedingungen gilt:
F̃i =
r
X
λk
k=1
125
∂fk
∂xi
λk fki
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Lösungsstrategie:
(i) ẍi aus LG 1. Art in die nach der Zeit differenzierten Nebenbedingungen einsetzen
(ii) aus diesen r Gleichungen erhält man die λk
(iii) λk in die LG 1. Art einsetzen
(iv) resultierende Bewegungsgleichungen lösen → xi = xi (t)
Beispiel: Massenpunkt auf schiefer Ebene (vgl. 3.1.3)
eingeprägte Kraft: F~ = −mg e~z
Nebenbedingung: f (x, y, z) = z − x tan α = 0
⇒
∂f
= − tan α
∂x
∂f
=1
∂z
Lagrangesche Gleichungen 1. Art:
mẍ = −λ tan α
mÿ = 0
mz̈ = −mg + λ
126
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
(i) Wir differenzieren die Nebenbedingung nach der Zeit:
z̈ − ẍ tan α = 0
und setzen die ẍi aus den LG 1. Art ein:
λ
λ
−g + + tan α tan α = 0
m
m
| {z } | {z }
−ẍ
z̈
(ii) λ bestimmen:
λ
m
(1 + tan2 α) = g
{z
}
|
1
cos2 α
λ = mg cos2 α
(iii) λ in LG 1. Art eliminieren
ẍ = −g sin α cos α
ÿ = 0
z̈ = g(−1 + cos2 α) = −g sin2 α
(iv) Resultierende Bewegungsgleichungen lösen:
x = s cos α
s̈ =
ẍ
= −g sin α
cos α
(bekanntes Ergebnis aus 3.1.3)
Zwangskraft für holonome Bedingungen:
F̃i =
r
P
k=1
k
λk ∂f
∂xi
˜
~ = mg cos2 α∇(z
~ − x tan α)
→ F~ = λ∇f
127
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Komponentenweise ausgedrückt:
F˜x = mg cos2 α(− tan α) = −mg sin α cos α
F˜y = 0
F˜z = mg cos2 α
(bekanntes Ergebnis aus 3.1.3)
~ bringt unmittelbar zum Ausdruck, daß die Zwangskraft senkrecht
Bemerkung: F̃ ∼ ∇f
auf der schiefen Ebene steht.
Energiebilanz
Aus 3.1.3 wissen wir
dT
= P + P̃
dt
wobei
3N
X
P̃ =
F̃i ẋi
i=1
die Leistung der Zwangskräfte ist. Mit
F̃i =
r
X
λk fki
k=1
folgt
P̃ =
r
X
k=1
λk
3N
X
fki ẋi
i=1
Wobei für die Nebenbedingungen
3N
X
fki ẋi + fk0 = 0
i=1
gilt.
128
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit
P̃ = −
r
X
λk fk0
k=1
und die Energiebilanz lautet
r
X
dT
=P −
λk fk0
dt
k=1
Speziell für holonome Bedingungen gilt
r
X ∂fk
dT
=P−
λk
dt
∂t
k=1
Besitzen die eingeprägten Kräfte ein Potential, so gilt (vgl. 2.3.3)
r
d
∂U X
(T + U ) =
−
λk fk0
dt
∂t
k=1
bzw. speziell für holonome Bedingungen
r
d
∂U X ∂fk
(T + U ) =
−
λk
dt
∂t
∂t
k=1
D.h. die aus rheonomen Bindungen resultierenden Zwangskräfte tragen i.A. zur Leistung bei und verändern die Energie des MP-Systems. Ist das System konservativ und
skleronom, so gilt die Energieerhaltung.
129
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
3.2.2 Lagrangesche Gleichungen 2. Art
Für Systeme mit vielen Massenpunkten und vielen Nebenbedingungen sind die Lagrangeschen Gleichungen 1. Art oft nicht wirklich zielführend, da 3N +r Gleichungen zu lösen
sind.
Effizienter wäre es ein Verfahren zu benutzen, das von vornherein auf die f = 3N − r
Freiheitsgrade abstellt.
Wir betrachten N Massenpunkte mit r Nebenbedingungen der Form
fk (xj , t) = fk (x1 , x2 , . . . , x3N , t) = 0
k = 1, 2, . . . , r
Diese r Nebenbedingungen bilden ein Gleichungssystem in den xj , das für r < 3N unterbestimmt ist, d.h. f = 3N − r Koordinaten bleiben unbestimmt.
Wir können die xi als Funktion der Freiheitsgrade xj darstellen
xi = xi (xj1 , . . . , xjf , t)
i = 1, . . . , 3N j = 1, . . . , f
Die Koordinaten xj sind dann durch keine Nebenbedingungen mehr eingeschränkt.
Anstelle der beliebig wählbaren f Koordinaten xj können auch f beliebig wählbare (linear
unabhängige) Kombinationen dieser Koordinaten verwendet werden
qα = qα (xj1 , . . . , xjf , t)
α = 1, . . . , f
die dem System eventuell besser angepaßt sind.
Wir schreiben allgemein
xi = xi (qα , t) ≡ xi (q1 , q2 , . . . , qf , t)
i = 1, 2, . . . , 3N α = 1, 2, . . . , f
wobei die keinerlei Nebenbedingungen unterworfenen Koordinaten qα als generalisierte
Koordinaten bezeichnet werden.
130
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Durch Zeitableitung ergeben sich die generalisierten Geschwindigkeiten q˙α . Es gilt
f
X
∂xi
∂xi
q˙α +
ẋi =
∂qα
∂t
α=1
⇒
∂
∂ q˙α
∂ ẋi
∂xi
=
∂ q˙α
∂qα
xi = xi (qα , t), daraus folgt für die virtuellen Verrückungen
δxi =
f
X
∂xi
δqα
∂qα
α=1
Dieses setzen wir in das d’Alembertsche Prinzip ein:
3N
X
(mi ẍi − Fi )δxi = 0
i=1
f
X
∂xi
δqα = 0 bzw.
∂qα
α=1
i=1
#
" 3N
f
X
X
∂xi
δqα = 0
(mi ẍi − Fi )
∂qα
3N
X
α=1
(mi ẍi − Fi )
i=1
Da die δqα frei wählbar sind, muß folgendes gelten
3N
X
i=1
(mi ẍi − Fi )
∂xi
=0
∂qα
131
α = 1, 2, . . . , f
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir schreiben diese Bewegungsgleichung noch etwas um. Es gilt:
3N
X
3N
mi ẍi
i=1
3N
d X
∂xi
∂xi X
∂ ẋi
=
mi ẋi
−
mi ẋi
∂qα
dt
∂qα
∂qα
i=1
k
∂ x˙i
∂ q˙α
3N
=
3N
d X
∂ ẋi X
∂ ẋi
−
mi ẋi
mi ẋi
dt
∂ q˙α
∂qα
i=1
d ∂
=
dt ∂ q˙α
i=1
3N
X
i=1
|
d.h.
i=1
3N
X
mi ẍi
i=1
3N
1
∂ X1
2
mi ẋi −
mi ẋi 2
2
∂qα
2
i=1
{z
}
|
{z
}
T
T
d ∂T
∂T
∂xi
=
−
∂qα
dt ∂ q˙α ∂qα
wobei die kinetische Energie als Funktion der generalisierten Koordinaten und Geschwindigkeiten angesehen wird
T = T (qα , q˙α , t)
3N
X
i=1
Fi
∂xi
=: Φα (qα , q˙α , t) . . . generalisierte Kraft
∂qα
Damit lauten die Bewegungsgleichungen
d ∂T
∂T
−
= Φα
dt ∂ q˙α ∂qα
α = 1, 2, . . . , f
Besitzen die eingeprägten Kräfte Fi ein Potential U = U (xi , t)
Fi = −
132
∂U
∂xi
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
folgt für Φα
Φα =
3N
X
i=1
3N
X ∂U ∂xi
∂U
∂xi
=−
=−
Fi
∂qα
∂xi ∂qα
∂qα
i=1
wobei die potentielle Energie als Funktion der generalisierten Koordinaten und der Zeit
angesehen wird: U = U (qα , t)
⇒
∂U
=0
∂ q˙α
Wir können daher schreiben
Φα = −
d ∂U
∂U
+
∂qα dt ∂ q˙α
| {z }
0
Wir definieren die
Lagrange-Funktion des Systems
L = L(qα , q˙α , t) = T − U
und finden damit eine kompakte Notation für die Bewegungsgleichung in generalisierten
Koordinaten.
Lagrangesche Gleichungen 2. Art
∂L
d ∂L
−
=0
dt ∂ q˙α ∂qα
α = 1, 2, . . . , f
Wir haben jetzt f gewöhnliche Differentialgleichungen 2. Ordnung zur Bestimmung der
qα (t). Die Anzahl der Gleichungen ist gleich der Anzahl der Freiheitsgrade. Die Nebenbedingungen treten nicht mehr explizit auf.
133
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Lösungsstrategie:
(i) formuliere die Zwangsbedingungen
(ii) finde die verallgemeinerten Koordinaten
(iii) stelle die Lagrange-Funktion L = T − U auf
(iv) leite die Lagrange-Gleichungen 2. Art ab und löse sie
(v) transformiere zurück auf die ursprünglichen (anschaulichen) Koordinaten
(der letzte Schritt ist nicht immer notwendig und nicht immer möglich)
Beispiel: Rollpendel
m1 bewege sich reibungsfrei entlang x. Welche Bahnen beschreiben m1 und m2 unter
dem Einfluß der Schwerefeldes?
(i) 4 holonom-skleronome Zwangsbedingungen
z1 = z2 = 0
y1 = 0
(x1 − x2 )2 + y22 − R2 = 0
damit verbleiben 6 − 4 = 2 Freiheitsgrade
134
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
(ii) generalisierte Koordinaten: x1 und ϕ
Transformationsformeln
x2 = x1 + R sin ϕ ⇒ x˙2 = x˙1 + ϕ̇R cos ϕ
y2 = R cos ϕ ⇒ y˙2 = −ϕ̇R sin ϕ
(iii) Lagrange-Funktion
1
1
1
m2 2 2
T = m1 x˙1 2 + m2 (x˙2 2 + y˙2 2 ) = (m1 + m2 )x˙1 2 +
(R ϕ̇ + 2Rx˙1 ϕ̇ cos ϕ)
2
2
2
2
U = −m2 gR cos ϕ
L=T −U =
m1 + m2 2 m2 2 2
x˙1 +
(R ϕ̇ + 2Rx˙1 ϕ̇ cos ϕ) + m2 gR cos ϕ
2
2
(iv) LG 2. Art lösen
d ∂L
dt ∂ x˙1
−
∂L
∂x1
=0
k
0
⇒
∂L
∂ x˙1
=: p1 = (m1 + m2 )x˙1 + m2 Rϕ̇ cos ϕ = const.
(Gesamtimpuls des Systems in x-Richtung)
p1 . . . verallgemeinerter Impuls zur Koordinate x1
Wir lösen nach x˙1 auf:
x˙1 =
p1
m1 +m2
x1 (t) = x1 (0) +
−
m2
m1 +m2 Rϕ̇ cos ϕ
p1
m1 +m2 t
−
135
m2
m1 +m2 R(sin ϕ(t)
Rt
dt0
0
− sin ϕ(0))
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir wählen die Anfangsbedingungen
x1 (0) = 0,
x˙1 (0) = −
ϕ(0) = 0,
ϕ̇(0) = ω0
| {z }
m2
Rω0
m1 + m2
⇒p1 =0
damit
x1 (t) = −
m2
R sin ϕ(t)
m1 + m2
D.h. der erste Massenpunkt schwingt um seine Ruhelage. Aus den Transformationsformeln folgt für den zweiten Massenpunkt
x2 (t) = x1 (t) + R sin ϕ(t) =
m1
R sin ϕ(t)
m1 + m2
y2 (t) = R cos ϕ(t)
Es gilt
x2 (t)2
m1 R
m1 +m2
2 +
y2 (t)2
=1
R2
D.h. der zweite Massenpunkt bewegt sich auf einer Ellipse
mit horizontaler Halbachse
a=
m1 R
m1 + m2
und vertikaler Halbachse
b=R>a
136
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Das Problem ist noch nicht vollständig gelöst. Wir erhalten die Zeitabhängigkeit von ϕ(t)
aus
d ∂L ∂L
−
=0
dt ∂ ϕ̇ ∂ϕ
∂L
= m2 R2 ϕ̇ + m2 Rx˙1 cos ϕ
∂ ϕ̇
d ∂L
= m2 R2 ϕ̈ + m2 Rx¨1 cos ϕ − m2 Rx˙1 ϕ̇ sin ϕ
dt ∂ ϕ̇
∂L
= −m2 Rx˙1 ϕ̇ sin ϕ − m2 gR sin ϕ
∂ϕ
⇒ Rϕ̈ + x¨1 cos ϕ + g sin ϕ = 0
Näherung für kleine Winkel: cos ϕ ≈ 1, sin ϕ ≈ ϕ.
m2
R sin ϕ(t)
m1 + m2
m2
x˙1 (t) = −
R cos ϕ(t) · ϕ̇
m1 + m2
m2
m2
x¨1 (t) = −
R(ϕ̈ cos ϕ − ϕ̇2 sin ϕ) ≈ −
Rϕ̈
m1 + m2
m1 + m2
x1 (t) = −
Damit gilt näherungsweise
Rϕ̈ −
m2
Rϕ̈ + gϕ = 0
m1 + m2
m1
ϕ̈
R + gϕ = 0
m1 + m2
g m1 + m2
ϕ=0
ϕ̈ +
R m1
(Differentialgleichung des harmonischen Oszillators, vgl. 1.4)
r
Schwingungsfrequenz ω =
137
g m1 + m2
R m1
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die gewählten Anfangsbedingungen führen auf
ϕ(t) =
ω0
sin ωt
ω
Generalisierter Impuls
Generalisierte Impulse sind definiert durch
pα :=
∂L
∂T
=
∂ q˙α
∂ q˙α
Nach den Lagrangeschen Gleichungen 2. Art
d ∂L
∂L
−
=0
dt ∂ q˙α ∂qα
folgt
p˙α =
∂T
∂L
=
+ Φα
∂qα
∂qα
↑
generalisierte Kräfte
Sei speziell ein freies System gegeben durch
L=
3N
X
mi
i=1
2
ẋi 2 − U (x1 , . . . , x3N , t)
∂L
= mi ẋi = pi
∂ ẋi
d.h. die generalisierten Impulse stimmen mit den gewöhnlichen Impulsen überein und
Φi = −
∂U
= Fi
∂xi
die generalisierten Kräfte entsprechen den gewöhnlichen Kräften.
138
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Die Lagrangeschen Gleichungen 2. Art
d ∂L
∂L
−
= p˙i − Fi = 0
dt ∂ ẋi ∂xi
ergeben die bekannten Newtonschen Bewegungsgleichungen des freien Systems
mẍi = Fi
3.2.3 Erhaltungssätze und Symmetrien
Erhaltungssätze für physikalische Größen sind Ausdruck von Symmetrien
Energieerhaltung ⇔ Homogenität der Zeit
Die Lagrange-Funktion eines abgeschlossenen Systems L = L(qα , q˙α , t) ist invariant gegenüber einer zeitlichen Transformation t → t + δt, d.h.
L(qα , q˙α , t + δt) = L(qα , q˙α , t) + δL
mit δL =
wobei wegen der Homogenität der Zeit
∂L
∂t
∂L
δt
∂t
= 0 gilt.
139
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Was bedeutet das physikalisch?
f ∂L
dL X ∂L
∂L
q˙α +
q¨α +
=
dt
∂qα
∂ q˙α
∂t
α=1
f
∂L
d X ∂L
q˙α +
=
dt
∂ q˙α
∂t
(∗)
d
⇒
dt
α=1
f
X
α=1
∂L
d ∂L
=
dt ∂ q˙α
∂qα
(∗) :
!
∂L
∂L
q˙α − L = −
∂ q˙α
∂t
k
0
f
X
∂L
q˙α − L = const.
⇒
∂ q˙α
α=1
Nur die kinetische Energie hängt von der Geschwindigkeit ab, d.h.
f
f
X
X
∂L
∂T
q˙α =
q˙α
∂ q˙α
∂ q˙α
α=1
α=1
Für skleronome Bedingungen ist die kinetische Energie eine homogene Funktion 2. Grades
in den q˙α :
T (qα , λq˙α ) = λ2 T (qα , q˙α )
Nach dem Eulerschen Theorem über homogene Funktionen gilt (vgl. 2.3.4)
f
X
∂T
q˙α = 2T
∂ q˙α
α=1
damit
f
X
∂L
q˙α − L = 2T − (T − U ) = T + U = E = const.
∂ q˙α
α=1
D.h. die Energieerhaltung ist Ausdruck der Invarianz der Lagrange-Funktion gegenüber
zeitlicher Transformationen, d.h. Ausdruck der Homogenität der Zeit.
140
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Impuls ⇔ Homogenität des Raumes
Die Lagrange-Funktion eines abgeschlossenen Systems hängt von den Abständen der
Massenpunkte, aber nicht von deren absoluten Koordinaten ab. L ist invariant unter
räumlichen Translationen.
r~ν → r~ν + δ~r ⇒ L → L + δL
N
P
~ r~ L
mit δL =
δ~r · ∇
ν
ν=1
Wegen der Homogenität des Raumes ist δL = 0
N
X
⇒
~ r~ L = 0
∇
ν
ν=1
Wir betrachten die Translationsvariable ~r als generalisierte Koordinate
N
X
∂L
d ∂L
~ ~r L =
~ r~ L = 0
=
=∇
∇
ν
dt ∂~r˙
∂~r
ν=1
⇒
∂L
= const.
∂~r˙
N
N
N
N
ν=1
ν=1
ν=1
ν=1
X
X
∂L X ~
(∗) X
~ ˙T =
=
∇r~˙ν L =
∇
mν r~˙ν =
p~ν = p~
r
~
ν
∂~r˙
(∗): in L hängt nur T von r~˙ν ab.
Hieraus folgt die Erhaltung des Gesamtimpulses des Systems.
p~ = const.
ist Ausdruck der Homogenität des Raumes.
141
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Drehimpulserhaltung ⇔ Isotropie des Raumes
Isotropie des Raumes bedeutet, daß sich die Physik eines abgeschlossenen Systems bei
einer Drehung nicht ändert, d.h. unter der Transformation
r~ν → r~ν + δ r~ν , δ r~ν = δ ϕ
~ × r~ν
L → L + δL
soll die Lagrange-Funktion unverändert bleiben, also δL = 0.
δL =
N
X
~ r~ L = δ ϕ
δ r~ν · ∇
~
ν
ν=1
N
X
~ r~ L = 0
r~ν × ∇
ν
ν=1
Wir betrachten für eine gewählte feste Achse den Drehwinkel ϕ als generalisierte Koordinate auf
d ∂L
∂L
∂L
=
⇒
= const.
∂ϕ
dt ∂ ϕ̇
∂ ϕ̇
0=
Differential von L unter der Transformation:
dL =
=
N
X
ν=1
N
X
~ r~ L +
dr~ν · ∇
ν
N
X
~ ˙ L + ...
dr~˙ν · ∇
r~ν
ν=1
~ r~ L +
(d~
ϕ × r~ν ) · ∇
ν
ν=1
= d~
ϕ·
N
X
~ ˙ L + ...
(dϕ
~˙ × r~ν ) · ∇
r~ν
ν=1
N
X
~ r~ L + dϕ
r~ν × ∇
~˙ ·
ν
ν=1
N
X
ν=1
r~ν × p~ν
↑
s.o.
d.h.
N
N
ν=1
ν=1
X
X
∂L
~ = const.
= e~ω ·
r~ν × p~ν = e~ω
L~ν = e~ω · L
∂ ϕ̇
Die Invarianz der Lagrange-Funktion unter Drehung um eine beliebige Achse bedeutet
also die Erhaltung des Gesamtdrehimpulses.
142
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Zyklische Koordinaten
Systemangepaßte generalisierte Koordinaten qα
Transformation:
qα → qα + δqα
L → L + δL = L +
falls δL = 0 ⇔
∂L
δqα
∂qα
∂L
=0
∂qα
k
d ∂L
dt ∂ q˙α
⇒ Erhaltungssatz
∂L
= const.
∂ q˙α
Generalisierte Koordinaten, von denen die Lagrange-Funktion nicht abhängt, heißen zyklische Koordinaten. Sie stellen Symmetriekoordinaten des Systems dar und geben Anlaß
zu Erhaltungssätzen.
Erinnerung: Rollpendel in 3.2.2; x1 war zyklische Variable, entsprach Erhaltung des Gesamtimpulses p1
Beispiel: Zwei-Körper-Problem (vgl. 2.3.6)
Zwei Massenpunkte, die über eine abstandsabhängige Zentralkraft miteinander wechselwirken
1
1
L = m1 |r~˙1 |2 + m2 |r~˙2 |2 − U (|r~2 − r~1 |)
2
2
143
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir führen Relativ- und Massenmittelpunktskoordinaten ein
~r = r~2 − r~1
m~
rc = m1 r~1 + m2 r~2
m2
~r
m
m1
r~2 = r~c +
~r
m
⇒ r~1 = r~c −
(m = m1 + m2 )
(vgl. 2.3.6)
damit
m2 ˙ ˙
m2
r~c · ~r
|r~˙1 |2 = |r~˙c |2 + 22 |~r˙ |2 − 2
m
m
m2
m1 ˙ ˙
|r~˙2 |2 = |r~˙c |2 + 21 |~r˙ |2 + 2
r~c · ~r
m
m
m1 ˙ 2 m2 ˙ 2 1
1 m1 m22 + m2 m21 ˙ 2
|r~1 | +
|r~2 | = m|r~˙c |2 +
|~r|
2
2
2
2 (m1 + m2 )2
|
{z
}
m1 m2 (m1 +m2 )
=µ
(m1 +m2 )(m1 +m2 )
µ . . . reduzierte Masse
Damit nimmt die Lagrange-Funktion die Form
1
1
L = m|r~˙c |2 + µ|~r˙ |2 − U (|~r|)
2
2
an, ist additiv in Massenmittelpunkts- und Relativbewegung.
Die Massenmittelpunktskoordinate ist zyklisch ⇒ Impulserhaltungssatz
144
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
4 Hamiltonsche Mechanik
4.1 Prinzip der kleinsten Wirkung
Bisher gelangten wir mit den Newtonschen Bewegungsgleichungen und dem d’Alembertschen Prinzip zu den Lagrangeschen Gleichungen 2. Art. Man kann jedoch zeigen, daß
den Lagrangeschen Gleichungen ein fundamentales Prinzip, das Hamiltonsche Prinzip
oder Prinzip der kleinsten Wirkung zugrunde liegt, das von allgemeiner und zentraler
Bedeutung für die Physik ist.
Wir betrachten die „Bahnkurve“ eines Massenpunktsystems mit f Freiheitsgraden im
f -dimensionalen Konfigurationsraum der generalisierten Koordinaten qα
qα = qα (t)
Wir ordnen jedem Punkt P auf qα (t) einen infinitesimal benachbarten Punkt P 0 so zu,
daß P und P 0 jeweils zum gleichen Zeitpunkt gehören.
qα = qα (t) → qα0 = qα0 (t)
δqα (t) = qα0 (t) − qα (t), δt = 0
d.h. die Variationen der generalisierten Koordinaten sind virtuelle Verrückungen.
145
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
d
δqα (t) = q˙α0 (t) − q˙α (t) = δ q˙α (t)
dt
Wir betrachten die Funktion L(qα , q˙α , t) und deren Variation, d.h. die Differenz der Funktion auf der wirklichen Bahn und der variierten Bahn.
δL = L(qα0 , q˙α0 , t) − L(qα , q˙α , t) = L(qα + δqα , q˙α + δ q˙α , t) − L(qα , q˙α , t)
Für kleine Variationen δqα und δ q˙α folgt dann
δL =
f X
∂L
∂L
δqα +
δ q˙α
∂qα
∂ q˙α
α=1
Erinnerung 3.2.2, aus dem d’Alembertschen Prinzip
3N
X
(mi ẍi − Fi )δxi =
f X
d ∂L
∂L
−
δqα = 0
dt ∂ q˙α ∂qα
α=1
i=1
folgten die Lagrangeschen Gleichungen, da die δqα frei wählbar sind. Es gilt
d ∂L
dt ∂ q˙α
d
δqα =
dt
∂L
δqα
∂ q˙α
−
∂L d
δqα
∂ q˙α |dt{z }
δ q˙α



X
f
f 
X
 d ∂L

d ∂L
∂L


d.h.
δqα =
δq
+
δ
q
˙
α
α
 dt ∂ q˙α

dt ∂ q˙α
∂ q˙α


α=1
α=1 |
{z }
∂L
∂qα
=
f X
∂L
α=1
|
∂L
δqα +
δ q˙α
∂qα
∂ q˙α
{z
}
δL(siehe oben)
146
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
D.h. die einer Variation der Bahnkurve entsprechende Variation der Lagrange-Funktion
ist
f
X
d ∂L
δqα
δL =
dt ∂ q˙α
α=1
Zt2
dt
t1
t2
Zt2
dtδL =
f
X
∂L
δqα ∂ q˙α
α=1
t1
t1
Wir wählen die Vergleichsbahn so, daß Anfangs- und Endpunkte mit der wirklichen
Bahnkurve übereinstimmen:
δqα (t1 ) = δqα (t2 ) = 0
damit
Zt2
Zt2
dtδL = δ
t1
dtL = 0
t1
Wir definieren
Wirkung
Zt2
S=
dtL
t1
und erhalten
δS = 0
Hamiltonsches Prinzip oder Prinzip der kleinsten Wirkung
Die von einem MP-System im Konfigurationsraum tatsächlich durchlaufene Bahnkurve
zeichnet sich gegenüber den zugelassenen Vergleichsbahnen dadurch aus, daß für sie die
147
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wirkung einen Extremwert - meistens ein Minimum - annimmt.
Bemerkung: Hamiltonsches Prinzip in der Optik: Fermatsches Prinzip
Zs2
ds · n(s) = Extremum
↑
s1
Brechzahl
Wir können umgekehrt auch vom Hamiltonschen Prinzip starten und daraus die Lagrangeschen Gleichungen ableiten:
Zt2
Zt2
dtL =
0 = δS = δ
dt
t1
t1
Zt2
=
"
dt
d
δqα +
∂qα
dt
t1
Zt2
f X
∂L
dt
t1
α=1
f X
∂L
α=1
=
f X
∂L
α=1
∂L
δqα +
δ q˙α
∂qα
∂ q˙α
d ∂L
−
∂qα dt ∂ q˙α
∂L
δqα
∂ q˙α
−
#
d ∂L
dt ∂ q˙α
f
X
∂L
δqα +
δqα
∂ q˙α
α=1
|
δqα
t2
t1
{z
0
}
Da die δqα frei wählbar sind, folgt
∂L
d ∂L
−
=0
∂qα dt ∂ q˙α
α = 1, 2, . . . , f
Bemerkungen:
• Mathematisch formuliert sind die Lagrange-Gleichungen die Lösung der EulerLagrangeschen Variationsaufgabe.
• Falls keine holonomen Nebenbedingungen gegeben sind, erhalten wir gegebenenfalls
andere Bewegungsgleichungen:
Legen wir z.B. die ursprünglichen 3N Koordinaten des Systems zugrunde, so folgt
148
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
für das Variationsproblem
Zt2
dt
" 3N X ∂L
d ∂L
−
∂xi dt ∂ ẋi
i=1
t1
Zt2
bzw.
#
δxi = 0
" 3N
#
X
dt
(Fi − mi ẍi )δxi = 0
i=1
t1
wobei nun die δxi nicht mehr frei wählbar sind, sondern gemäß
3N
X
fki δxi = 0
k = 1, 2, . . . , r
i=1
mit den z.B. anholonomen Nebenbedingungen verträglich sein müssen. Wir können
daher zunächst nur auf das d’Alembertsche Prinzip
3N
X
(Fi − mi ẍi )δxi = 0
i=1
schließen.
4.2 Hamiltonsche Gleichungen
Die Lagrange-Gleichungen liefern uns Bewegungsgleichungen des Systems in der Form
von f gewöhnlichen Differentialgleichungen 2. Ordnung. Manchmal ist es zweckmäßiger,
stattdessen mit 2f gewöhnlichen Differentialgleichungen 1. Ordnung zu rechnen.
Erinnerung 3.2.2: generalisierte Impulse
pβ :=
∂L
β = 1, 2, . . . , f
∂ q˙β
d.h. aus L = L(qα , q˙α , t) folgen die generalisierten Impulse pβ = pβ (qα , q˙α , t)
Umstellen liefert q˙α = q˙α (qβ , pβ , t).
149
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir untersuchen jetzt das totale Differential der Lagrange-Funktion
dL =
f X
∂L
∂qα
|{z}
α=1
d
= dt
=
=
f
X
dqα +
∂L
∂L
dq˙α +
dt
∂ q˙α
∂t
|{z}
pα
∂L
=p˙α
∂ q˙α
(p˙α dqα + pα dq˙α ) +
α=1
f
X
∂L
dt
∂t
[p˙α dqα + d(pα q˙α ) − q˙α dpα ] +
α=1
∂L
dt
∂t
d.h.
f
X
d
!
pα q˙α − L
=
α=1
|
f
X
(−p˙α dqα + q˙α dpα ) −
α=1
{z
H
∂L
dt
∂t
}
Offensichtlich hängt H von qα , pα und t ab, d.h. wir sind durch eine sogenannte LegendreTransformation zu einer neuen Funktion mit neuen Variablen gekommen, das ist die
Hamilton-Funktion des Systems
H = H(qα , pα , t) =
f
X
pα q˙α − L
α=1
Bemerkung: Erinnerung 3.2.3, dort wurde bereits gezeigt, daß für skleronome Bedingungen H gerade die Energie des Systems darstellt.
150
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Das vollständige Differential der Hamilton-Funktion ist gegeben durch
dH =
f X
∂H
α=1
∂H
dqα +
dpα
∂qα
∂pα
+
∂H
dt
∂t
Koeffizientenvergleich liefert
p˙α = −
∂H
,
∂qα
q˙α =
∂H
∂pα
Hamiltonsche oder kanonische Gleichungen
∂H
∂L
=−
∂t
∂t
D.h. wir haben jetzt 2f gewöhnliche DGL 1. Ordnung als Bewegungsgleichungen für die
2f unbekannten Funktionen qα (t) und pα (t).
Energieerhaltung:
f X
∂H dqα
dH
∂H dpα ∂H
=
+
+
dt
∂qα dt
∂pα dt
∂t
α=1
=
f
X
α=1
k
k
−p˙α
q˙α
∂H
(−p˙α q˙α + q˙α p˙α ) +
|
{z
} ∂t
0
Hängt die Hamilton-Funktion nicht explizit von der Zeit ab, ist sie Erhaltungsgröße.
∂H
dH
=0 ⇒
= 0 ⇒ H = E = const.
↑
∂t
dt
(3.2.3)
151
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Lösungsstrategie
(i) formuliere die Zwangsbedingungen
(ii) finde die verallgemeinerten Koordinaten
(iii) drücke T und V durch die generalisierten Koordinaten und Geschwindigkeiten aus
(iv) bestimme die generalisierten Impulse
pj =
∂T
∂ q˙j
(v) eliminiere damit die q˙j und bilde die Hamilton-Funktion
H(q1 , . . . , qf , p1 , . . . , pf ) = T + V
(vi) identifiziere eventuelle zyklische Koordinaten, die zugehörigen (zeitlich konstanten)
Impulse können aus den Anfangsbedingungen bestimmt werden
(vii) stelle für alle (nicht zyklischen) Variablen die Bewegungsgleichungen auf
−
∂H
= p˙j ,
∂qj
∂H
= q˙j
∂pj
und löse sie
(viii) transformiere zurück auf die ursprünglichen (anschaulichen) Koordinaten
152
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beispiel: Gleiten auf schräger Schiene im Schwerefeld der Erde
(i) y = 0, Nebenbedingung: z + x tan α = 0
(ii) generalisierte Variable: Weg s des Massenpunktes. Es gilt:
x = s cos α,
y = 0,
z = −s sin α
ẋ = ṡ cos α,
ẏ = 0,
ż = −ṡ sin α
(iii)
⇒T =
m
m
m 2
(ẋ + ẏ 2 + ż 2 ) = (ṡ2 cos2 α + ṡ2 sin2 α) = ṡ2
2
2
2
V = mgz = −mgs sin α
(iv) generalisierter Impuls
p=
∂T
= mṡ
∂ ṡ
(v) Hamilton-Funktion
H =T +V =
p2
− mgs sin α
2m
(vi) In diesem Beispiel gibt es keine zyklischen Koordinaten, d.h. es gibt keine zeitlich
konstanten Impulse
153
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
(vii) Bewegungsgleichungen
−
∂H
= ṗ ⇒ mg sin α = ṗ
∂s
p
∂H
= ṡ ⇒
= ṡ
∂p
m
Integration liefert:
p(t) = p0 + (mg sin α)t
Zt
s(t) = s0 +
p(t0 ) 0
dt
m
0
= s0 +
p0
t2
t + (g sin α)
m
2
Wir wählen die Anfangsbedingungen p0 = s0 = 0, damit erhalten wir die Bahnkurve
durch Rücktransformation
~r(t) = (x(t), y(t), z(t)) = (cos α, 0, − sin α)(g sin α)
Bemerkung: Es gilt die Energieerhaltung
H=
p2
− mgs sin α
2m
mit
p = (mg sin α)t
s = (g sin α)
t2
(Spezielle Anfangsbedingungen)
2
154
t2
2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
gilt
H=
m2 g 2 sin2 α 2
t2
t − mg 2 sin2 α = 0 = const.
2m
2
4.3 Poisson-Klammern
Wir betrachten eine physikalische Größe A = A(qα , pα , t), wobei für qα , pα die kanonischen Gleichungen
q˙α =
∂H
,
∂pα
p˙α = −
∂H
∂qα
gelten, dann gilt:
f dA X ∂A
∂A
∂A
=
q˙α +
p˙α +
dt
∂qα
∂pα
∂t
α=1
f X
∂A ∂H
∂A ∂H
∂A
=
−
+
∂qα ∂pα ∂pα ∂qα
∂t
α=1
Wir definieren die Poisson-Klammer {A, B} zweier Größen A und B durch
f X
∂A ∂B
∂A ∂B
{A, B} =
−
∂qα ∂pα ∂pα ∂qα
α=1
damit lautet die Bewegungsgleichung für A
dA
∂A
= {A, H} +
dt
∂t
Speziell für A = qα bzw. A = pα gilt dann offensichtlich
p˙α = {pα , H} ,
q˙α = {qα , H}
kanonische Gleichungen in symmetrischer Form
155
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Für die Poisson-Klammern gelten folgende Regeln
{A, B} = − {B, A}
{(A + B), C} = {A, C} + {B, C}
{AB, C} = A {B, C} + {A, C} B
{A, pα } =
∂A
,
∂qα
{A, qα } = −
∂A
∂pα
{A, {B, C}} + {B, {C, A}} + {C, {A, B}} = 0 (Jacobi-Identität)
{qα , pβ } = δαβ
{qα , qβ } = {pα , pβ } = 0 (Beweis: Übung)
Falls A Erhaltungsgröße ist, gilt
0=
dA
∂A
= {A, H} +
dt
∂t
D.h. falls A nicht explizit von der Zeit abhängt, ist A Erhaltungsgröße, wenn
{A, H} = 0.
Wir betrachten
d
∂
{A, B} = {{A, B} , H} +
{A, B}
dt
∂t
156
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
mit {{A, B} , H} + {{H, A} , B} + {{B, H} , A} = 0
↑
Jacobi
folgt {{A, B} , H} = {A, {B, H}} + {B, {H, A}} = {A, {B, H}} + {{A, H} , B}
ferner gilt
∂
{A, B} =
∂t
∂A
,B
∂t
∂B
+ A,
∂t
so daß insgesamt
d
∂A
∂B
{A, B} = {A, {B, H}} + {{A, H} , B} +
, B + A,
dt
∂t
∂t
(
) (
)
∂A
∂B
=
{A, H} +
, B + A, {B, H} +
∂t
|
{z
}
|
{z ∂t }
dA
dt
dB
dt
Daraus folgt das
Poisson-Theorem
d
{A, B} =
dt
dA
,B
dt
dB
+ A,
dt
D.h. falls A und B Erhaltungsgrößen sind
dB
dA
=
=0
dt
dt
gilt dies auch für die Poisson-Klammer von A und B
d
{A, B} = 0 ⇒ {A, B} = const.
dt
Damit kann man gegebenenfalls neue Bewegungsintegrale für ein System finden.
157
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
5 Spezielle Relativitätstheorie
5.1 Grundlagen
5.1.1 Michelson-Experiment - Lorentzkontraktion
∧
1864: theoretisches Fundament des Elektromagnetismus = Maxwell-Gleichungen,
~ mit dem Magnetfeld B,
~ der elektridiese verknüpfen im Vakuum das elektrische Feld E
schen Ladungsdichte ρ sowie der elektrischen Stromdichte ~j:
~ ·B
~ =0
∇
~˙ = 0
~ ×E
~ +B
∇
~ ·E
~ = 1 ·ρ
∇
0
~ ×B
~ − 1 ·E
~˙ = µ0 · ~j
∇
c2
Vs
wobei µ0 = 4π · 10−7 Am
, 0 = 8, 854 · 10−12 VAs
m , 0 · µ0 =
1
c2
mit c = 3 · 108 m
s.
Bemerkungen:
• Die Maxwell-Gleichungen enthalten die Lichtgeschwindigkeit c als Naturkonstante!
• spezielle Lösung der Maxwell-Gleichungen: elektromagnetische Wellen (Lichtwellen), die sich im Vakuum mit c ausbreiten
158
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Probleme:
• Nach der Galilei-Transformation sollten sich Geschwindigkeiten linear addieren:
t0 = t
r~0 = ~r − ~v t
˙
r~0 = ~r˙ − ~v
k
k
v~0
~v˜
~v . . . Geschwindigkeit des gestrichenen Systems
v~0 . . . Geschwindigkeit im gestrichenen System
~v˜ . . . Geschwindigkeit um ungestrichenen System
d.h. der Beobachter sollte die Lichtgeschwindigkeit in Abhängigkeit vom Bewegungszustand der Lichtquelle messen können
• Medium, in dem sich Lichtquellen ausbreiten?
∧
(z.B. Schallwellen = Druckschwankungen)
Hypothese: Licht breitet sich im „Äther“ aus, eine Substanz die den leeren Raum sowie
andere Materie ausfüllt und durchdringt.
159
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Bewegung der Erde relativ zum Äther?
→ 1881 Michelson-Experiment in Potsdam (später genauer in den Zeiss-Werken in Jena)
Zeit, die das Licht von P zu S1 braucht:
t1 =
l1 + x
c
In dieser Zeit bewegt sich das Interferometer um x (mit v)
x
v
x
l1 + x
⇒ =
v
c
c
x
− 1 = l1
v
l1 vc
x=
1 − vc
t1 =
160
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beim Rückweg kommt P dem Licht um die Strecke x0 entgegen
l1 − x0
c
x0
0
t1 =
v
l1 vc
x0 =
1 + vc
t01 =
Gesamtweg des Lichts:
L1 = l1 + x + l1 − x0
l1 vc
l1 vc
= 2l1 +
−
1 − vc
1 + vc
2
2
2l1 1 − vc2 + l1 vc + vc2 − l1 vc −
=
2
1 − vc2
2l1
=
2
1 − vc2
Strahlengang senkrecht zu ~v :
Die Zeit, die das Licht von P zu S2 braucht
p
l22 + y 2
t2 =
c
ist gleich der Flugzeit des Spiegels
t2 =
161
y
v
v2
c2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
l2 + y 2
y2
⇒ 2 2 = 2
c v
1
l2
1
y 2 2 − 2 = − 22
c
v
c
y2 =
c2
l22
1
−
v2
y = l2 q
1
c2
v
c
1−
v2
c2
Das Problem ist symmetrisch, d.h. der Gesamtweg lautet:
v
u
q
u
2
L2 = 2 l2 + y 2 = 2tl22 + l22
v2
c2
1−
v2
c2
1
= 2l2 q
1−
v2
c2
Damit ergibt sich die Wegdifferenz
∆S = Lk − L⊥ = L1 − L2 =
2l1
1−
v2
c2
2l2
−q
1−
v2
c2
Einschub: Taylorentwicklung
Satz von Taylor: Eine Funktion f sei in (x0 −α, x0 +α), α > 0 (n+1)-mal differenzierbar.
Dann gilt für x ∈ (x0 − α, x0 + α)
f (x) =
n
X
f (i) (x0 )
i=0
mit Rn (x) =
i!
(x − x0 )i + Rn (x)
f (n+1) (x0 + β(x − x0 ))
(x − x0 )n+1
(n + 1)!
162
β ∈ (0, 1)
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beispiele:
f (x) =
1
1+x
x0 = 0
1
0
= −1
f (x0 ) = −
(1 + x)2 x=x0
⇒ f (x) = f (0) (x0 )x0 + f (1) (x0 )x1 + σ(x2 ) = 1 − x + σ(x2 )
d.h. für x 1 gilt
1
≈1−x
1+x
1
x0 = 0
1+x
1
1
− 23 0
f (x0 ) = − (1 + x) =−
2
2
x=x0
f (x) = √
1
⇒ f (x) = f (0) (x0 )x0 + f (1) (x0 )x1 + σ(x2 ) = 1 − x + σ(x2 )
2
d.h. für x 1 gilt
1
x
√
≈1−
2
1+x
Anwendung hier:
1
1−
v2
c2
1
q
∆S =
1−
2l1
1−
v2
c2
v2
c2
≈1+
v2
c2
≈1+
1 v2
2 c2
2l2
−q
1−
v2
c2
für v c
für v c
≈ 2(l1 − l2 ) + 2l1
163
v2
v2
− l2 2
2
c
c
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir rotieren den Versuchsaufbau um 90◦ (l1 ↔ l2 )
L1 →
2l2
1−
2l1
L2 → q
1−
v2
c2
v2
c2
∆S ⊥ = Lk − L⊥ = L2 − L1
2l1
=q
1−
v2
c2
−
2l2
1−
≈ 2(l1 − l2 ) − 2l2
v2
c2
v2
v2
+
l
1 2
c2
c
(k, ⊥ bezogen auf Lichtwellen)
⇒ ∆(∆S) = ∆S − ∆S ⊥ ≈ l1
v2
v2
+
l
2
c2
c2
Für v > 0 sollte daher eine orientierungsabhängige Interferenz auftreten. Problem: Das
Experiment findet keine Orientierungsabhängigkeit!
Lösungsmöglichkeiten:
a) Erde nimmt Äther mit (Michelson)
widerspricht der Fixsternaberration (damals mit Äther erklärt):
Wir müssen ein Fernrohr um α = arctan Ll = arctan vt
ct gegen die Senkrechte drehen,
um einen Fixstern zu sehen. Nach einem halben Jahr: v → −v ⇒ α → −α
164
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
b) Geschosshypothese: c → c ± v
widerlegt durch Doppelsternbeobachtung
c) Kontraktion jedes Körpers in Bewegungsrichtung um einen Faktor x
r
1−
l=
L1 =
2l1
1−
v2
c2
v 2
(Lorentz 1892)
c
→
2l1
q
1−
1−
v2
c2
v2
c2
2l1
=q
1−
v2
c2
damit
∆S = L1 − L2 → q
2l1
1−
v2
c2
2l2
−q
1−
2l1
∆S ⊥ = L2 (l1 ) − L1 (l2 ) → q
1−
v2
c2
v2
c2
2l2
−q
1−
v2
c2
⇒ ∆(∆S) = ∆S − ∆S ⊥ = 0
Übereinstimmung mit dem Experiment!
D.h. wir können das Konzept des Äthers beibehalten, wenn wir die Lorentzsche Kontraktionshypothese akzeptieren. Das Michelson-Experiment zeigt, dass die Messung einer
absoluten Geschwindigkeit, d.h. der Bewegung relativ zum absoluten System des Äthers
nicht möglich ist. Die Ätherhypothese kann (muss aber nicht) fallengelassen werden!
Relativitätsprinzip (Einstein 1905)
Alle Naturgesetze behalten ihre Gültigkeit in beliebigen Inertialsystemen.
(hier: Konstanz der Lichtgeschwindigkeit, d.h. Maxwell-Gleichungen)
165
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
5.1.2 Zeitdilatation
Die Galilei-Transformation
~r0 = ~r − ~v t
gilt nicht wegen der Lorentzkontraktion.
Was ist mit t0 = t? Ist die Zeit absolut?
Lichtpulsuhr:
jetzt bewegt sich die Uhr mit ~v :
Zeit, die das Licht von S1 zu S20 braucht:
p
L2 + y 2
t=
c
in dieser Zeit bewegt sich der Spiegel um y
t=
y
v
166
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
y2
L2 + y 2
=
2
v
c2
2
1
L
1
y2
− 2 = 2
2
v
c
c
⇒
v
y = Lq c
1−
v2
c2
Periode der bewegten Uhr
τ 0 = 2t =
2y
1
2L
q
=
v
c
|{z}
1−
τ
v2
c2
τ
=q
1−
v2
c2
⇒ Eine bewegte Uhr läuft langsamer!
Gilt das auch für andere Bewegungsrichtungen? Wir untersuchen eine parallel bewegte
Uhr:
Lorentz-Kontraktion
r
0
L =L
1−
v2
<L
c2
Lichtweg von S1 zu S20
∆S = L0 + x
167
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Zeit für Hinweg
L0 + x
x
t=
=
c
v
1 1
L0
x
=−
−
c v
c
L0 vc
L0
x=−
=
1 − vc
1 − vc
Der Rückweg von S20 zu S10 verkürzt
∆S 0 = L0 − x0
Zeit für Rückweg
x0
L0 − x0
=
t0 =
c
v
0
1
1
L
x0
+
=
v
c
c
L0 vc
L0
x0 =
=
1 + vc
1 + vc
Der Gesamtweg beträgt:
S = 2L0 + x − x0
r
v
v
v2
c
c
=L 1− 2 2+
−
c
1 − vc
1 + vc
r
v2
v
v
v 2 2 1 − c2 + c 1 + c −
=L 1− 2 ·
2
c
1 − v2
c
2
= Lq
1−
τ0 =
v2
c2
s
2L
1
q
=
c |{z}
c
1−
τ
v2
c2
τ
=q
1−
168
v2
c2
v
c
1−
v
c
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Bemerkungen:
• Die Zeitdilatation ist unabhängig von der Bewegungsrichtung!
• Die Lorentz-Kontraktion ist essentiell für die konsistente Beschreibung der bewegten Uhr
• Zwillingsparadoxon
Welcher Zwilling altert schneller, der auf der Erde oder einer im Raumschiff?
Antwort: der auf der Erde (Achtung: Beschleunigung, ART)
• Ist der Effekt im Flugzeug meßbar?
v ≈ 1000
τ0
1
=q
τ
1−
v2
c2
v
km
⇒
≈ 10−6
h
c
≈1+
1 v 2
1
≈ 1 + 10−12
2 c
2
Der Effekt ist mit einer Atomuhr leicht meßbar!
Problem: Durch die Flughöhe kommt es zu einer veränderten Gravitation, wir brauchen daher die Allgemeine Relativitätstheorie. Abschätzung:
1
!
∆Epot = mgh = ∆Ekin = mv 2
2
1 v 2 gh
−12
⇒
= 2 ≈ 10
2 c
c ↑
h ≈ 10 km
⇒ Die gravitative Zeitdilatation ist von gleicher Größenordnung wie die durch die
Bewegung verursachte.
169
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
• Höhenstrahlung
Die Lebensdauer eines Myons beträgt ca. 2, 2·10−6 s. Das entspricht einer Fluglänge
von maximal s = c · ∆τ ≈ 660 m. Der Nachweis erfolgt daher nur aufgrund der
Zeitdilatation!
5.1.3 Lorentz-Transformation
Die Lorentz-Kontraktion und die Zeitdilatation sind Ausdruck desselben Effekts!
Beispiel: Myonenzerfall
Im System der Erde ist die Fluglänge durch die Zeitdilatation verlängert:
1
x → xq
1−
v2
c2
= x0
Im (bewegten) Ruhesystem des Myons ist x0 durch die Lorentzkontraktion verkürzt:
r
x0 → x0
1−
v2
= x00 = x
c2
Wir suchen eine Transformation, die konsistent vom bewegten ins ruhende Bezugssystem
transformiert.
170
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Forderungen an die Transformation:
a) Homogenität und Isotropie des Raumes
b) Konstanz der Lichtgeschwindigkeit
c) Relativitätsprinzip
• Homogenität des Raumes:
Falls ein Körper in S die konstante Geschwindigkeit ~u hat, ist u~0 in S 0 ebenfalls
konstant. D.h. die Transformation ist linear:
x0 = a11 x + a12 t + c1
t0 = a21 x + a22 t + c2


0
y =y 
o.B.d.A. wegen ~v k e~x

z0 = z 
Ohne Beschränkung der Allgemeinheit gelten außerdem
t00


= t0 = 0 

x00 = x0 = 0 
171
⇒ c1 = c2 = 0
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Damit
x0 = a11 x + a12 t
t0 = a21 y + a22 t
Speziell für die Bewegung des Koordinatenursprungs von S 0 ergibt sich:
x0 = 0 = a11 x + a12 t
⇒−
a12
x
= = v ⇒ a12 = −a11 · v
a11
t
⇒ x0 = a11 (v)x − a11 (v) · v · t
= a11 (v)(x − v · t)
(∗)
• Relativitätsprinzip:
Wir können auch annehmen, daß S 0 in Ruhe ist und sich S mit −v bewegt. Daher
muß in Analogie gelten
x = a11 (−v)(x0 − (−v)t0 )
t → −t
Zeitspiegelung in S ~v → −~v
(∗∗)
ändert ~v =
d~
x
dt
läßt x unverändert
x →x
d.h.
x0


= a11 (v)x + a12 (v)t 
→

t0 = a21 (v)x + a22 (v)t 
172
x00 = a11 (−v)x − a12 (−v)t
t00 = a21 (−v)x − a22 (−v)t
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Mit x00 = x0 , t00 = −t0 (Zeitspiegelung in S 0 ) folgt:
a11 (−v) = a11 (v)
a12 (−v) = −a12 (v)
a21 (−v) = −a21 (v)
a22 (−v) = a22 (v)
⇒ a11 = a11 (v 2 ), hängt nicht vom Vorzeichen von v ab.
• Konstanz der Lichtgeschwindigkeit:
t = t0 = 0, S fällt mit S 0 zusammen.
Wir senden einen Lichtblitz aus. Dieser erreicht in S zum Zeitpunkt t den Ort x
x = ct
und in S 0 zum Zeitpunkt t0 den Ort x0
x0 = ct0
Damit in (∗)
v
x0 = a11 (v 2 )(x − vt) = a11 (v 2 )x 1 −
k
c
x
c
und in (∗∗)
v
x = a11 (v 2 )(x0 + vt0 ) = a11 (v 2 )x0 1 +
k
c
0
x
c
v
v
= a11 (v )a11 (v )x 1 +
1−
c
c
2
173
2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
⇒ a211 =
1
1−
v2
c2
1
d.h. a11 = q
1−
v
a12 = −a11 v = − q
1−
v2
c2
v2
c2
x − vt
x0 = q
2
1 − vc2
Damit in (∗∗)
x = a11 x0 + vt0
d.h.
x
0
−x
a11
r

v2
1
x − vt 
1− 2 ·x− q
=
2
v
c
1 − vc2
v2
1
−
x − x + vt
2
1
c
q
= ·
2
v
1− v
1
t =
v
0
c2
t − v2 x
t0 = q c
2
1 − vc2
Lorentz-Transformation mit ~v = v e~x
x − vt
x0 = q
2
1 − vc2
x0 + vt0
x= q
2
1 − vc2
t − v2 x
t0 = q c
2
1 − vc2
t0 + v2 x0
t= q c
2
1 − vc2
y 0 = y, z 0 = z
y = y0, z = z0
174
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
nichtrelativistischer Grenzfall v c:
1
q
1−
→ 1+
v2
c2
1 v2 3 v4
+
+ ...
2
8{zc4
|2 c
}
→0
es ergibt sich die Galilei-Transformation:
x0 = x − vt
t0 = t
y 0 = y, z 0 = z
Addition von Geschwindigkeiten?
In S gilt:
x = ut
In S 0 gilt mit x0 =
qx−vt
2
1− v2
c
und t0 =
t− v x
q c2
2
1− v2
(∗)
:
c
u0 =
x0
x − vt
=
0
t
t − cv2 x
175
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Additionstheorem der Geschwindigkeiten
(∗)
u0 =
u−v
1 − vu
c2
Bemerkungen:
• speziell u = c:
u0 =
c−v
=c
1 − vc
d.h. c ist die maximal erreichbare Geschwindigkeit (Ergebnis ändert sich nicht bei
v → −v!)
• speziell v c:
u0 = u − v
(Galilei-Transformation)
5.2 Raum-Zeit-Mannigfaltigkeit
5.2.1 Meßvorschriften und Gleichzeitigkeit
Galilei/Newton: absolute Zeit, wir können Gleichzeitigkeit festlegen mittels eines idealen
starren Körpers (unendlich große Signalgeschwindigkeit)
SRT: Lorentz-Transformation verknüpft Raum und Zeit


Zeitpunkte 
−→ Ereignispunkte in der Raum-Zeit-Mannigfaltigkeit

Raumpunkte 
Es ist daher eine sorgfältige Definition von Meßvorschriften und des Begriffs „Gleichzeitigkeit“ erforderlich.
176
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
(i) Zeitmessung
Wir betrachten eine bewegte Uhr, der Beobachter ruht in S.
cot ϑ =
v
v
⇔ ϑ = arccot
c
c
Wir betrachten das System S0 , in dem die Uhr ruht. Die t0 -Achse ist daher parallel zur
Weltlinie der Uhr.
Lorentz-Transformation:
t − v2 x
t0 = q c
2
1 − vc2
Die x0 -Achse ist definiert durch t0 = 0
⇒ ct =
v
x
c
⇒ tan ϕ =
v
v
⇔ ϕ = arctan
c
c
177
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Wir betrachten Ereignisse in S und S0 , z.B. zweimaliges Schlagen der Uhr (E1 , E2 )
Die Zeitdifferenz zwischen E1 und E2 hängt vom Bezugssystem und von der Meßvorschrift
ab.
• Annahme: synchronisierte Uhren bei xE1 und xE2 ruhen in S.
LT: tE1 =
t0,E1 + cv2 x0,E
q
2
1 − vc2
tE2 =
t0,E2 + cv2 x0,E
q
2
1 − vc2
⇒ tE2 − tE1 =
t0,E2 − t0,E1
q
2
1 − vc2
⇒ Zeitdilatation
178
(∗)
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
• Annahme: Rückmeldung von E2 bei xE2 an xE1 ist erforderlich
Die Signallaufzeit ∆t =
xE2 −xE1
c
muß addiert werden.
LT: xE1 =
x0,E + vt0,E1
q
2
1 − vc2
xE2 =
x0,E + vt0,E2
q
2
1 − vc2
⇒ ∆t =
v t0,E2 − t0,E1
c 1 − v22
c
Damit ergibt sich die Zeitdifferenz für einen bei xE1 ruhenden Beobachter
τE2 E1 = tE2 − tE1 + ∆t
1 + vc
= (t0,E2 − t0,E1 ) q
|
{z
} 1 − v2
(∗)
c2
τ0,E2 E1
s
= τ0,E2 E1
1+
1−
v
c
v
c
6= (∗)
Bemerkung: Wir betrachten eine Frequenz
f0 =
1
τ0,E2 E1
τ0,E2 E1
f0
⇒f =
τE2 E1
f=
1
τE2 E1
relativistischer Dopplereffekt
s
f=
1 − vc
f0
1 + vc
f0 . . . Frequenz der ruhenden Quelle
f . . . Frequenz, die dem Beobachter erscheint, wenn die Quelle sich mit v fortbewegt.
179
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Beispiel: Rotverschiebung der Spektren von Sternen, die sich von der Erde entfernen
Wir betrachten den nichtrelativistischen Grenzfall:
v
1 ⇒
c
p
1−
√1
1+ vc
v
c
→1−
→1−
1v 2
· f0 ≈
f ≈ 1−
2c
1v
2c
1v
2c
+ ...
+ ...
v 1 v2
1− +
c 4 |{z}
c2
!
· f0
→0
Nichtrelativistische Ableitung:
f=
1
f0
1 + vc
Längenmessung (1D, Länge l)
• Beobachter ruht in S
• Körper bewegt sich mit v in S, ruht in S0
Variante a)
Der Körper leuchtet kurz bei t0,E auf, d.h. die Messung ist gleichzeitig in S0 , aber nicht
gleichzeitig in S.
E1 , E2 . . . Endpunkte des Körpers
180
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
r
LT: l0 =
1−
v2
l
c2
l0 < l
Die gleichzeitig gemessene Länge ist kürzer.
Variante b)
Der Körper leuchtet ständig und wird im System S fotografiert, d.h. die Messung ist
gleichzeitig in S, aber nicht gleichzeitig in S0 .
1
LT: l0 = q
1−
Die gleichzeitig gemessene Länge ist kürzer.
181
v2
c2
l
l0 > l
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Variante c)
Der Körper wird mit einem Lichtblitz aus S angestrahlt und wir messen das gestreute
Licht, d.h. die Messung ist weder in S noch in S0 gleichzeitig. Der Lichtblitz erreicht
Anfangs- und Endpunkt des Körpers zu verschiedenen Zeiten.
s
LT: l0 =
1 − vc
l
1 + vc
l0 < l
⇒ Die gemessene Länge l ist von der Meßvorschrift abhängig!
182
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
5.2.2 Kausalität von Ereignissen
Wir entsenden einen Lichtblitz bei x = 0, t = 0.
(i) Bereich der Raum-Zeit, den wir beeinflussen können
(ii) Ereignispunkte, von denen wir Nachrichten empfangen können
(iii) Ereignispunkte, mit denen wir nicht kommunizieren können
Der kausale Bereich wird beschrieben durch
c2 t2 − ~x2 > 0
| {z }
t>0
=:s2
s2 . . . Abstand in der Raum-Zeit
s2 Lorentz-transformiert:
o.B.d.A Lorentz-Transformation in ~x-Richtung (sonst Rotation des Koordinatensystems)
s2 = c2 t2 − x2
183
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
mit x0 =
qx−vt
2
1− v2
c
und t0 =
t− v x
q c2
2
1− v2
folgt
c
s02 = c2 t02 − x02
=
v 2 x2
c2
c2 t2 − 2tvx +
1−
v2
c2
−
(c2 − v 2 )t2 − x2 1 −
=
1−
x2 − 2tvx + v 2 t2
1−
v2
c2
v2
c2
v2
c2
= c2 t2 − x2 = s2
⇒ s2 ist Lorentz-invariant.
⇒ Der kausale Bereich ist Lorentz-invariant.
⇒ Die Kausalität der Welt wird durch die SRT nicht in Frage gestellt!
5.3 Relativistische Mechanik
5.3.1 Masse und Energie
Wir betrachten ein Atom im angeregten Zustand:
Es geht durch Emission von 2 Photonen (Annahme: kein Impulsübertrag auf das Atom)
in den Grundzustand über.
184
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Energien der Photonen:
L01 = ~ω1
L02 = ~ω2
ω . . . Kreisfrequenz
~ . . . Plancksches Wirkungsquantum (~ = 1, 05 · 10−24 Js)
Im Ruhesystem des Atoms gelte ω1 = ω2 = ω
Die Energiebilanz lautet daher:
E0∗ = E0 + 2L0
mit L0 = ~ω
E0∗ . . . Energie des angeregten Atoms
E0 . . . Energie des Atoms im Grundzustand
Bis jetzt haben wir das Ruhesystem des Atoms betrachtet. Betrachten wir nun das Atom
aus Sicht eines bewegten Beobachters:
Der Beobachter sieht die Dopplerverschiebung
1 ± vc
ω
ω± = q
v2
1 − c2
1 ± vc
1 ± vc
⇒ L± = ~ω ± = |{z}
~ω q
= L0 q
2
2
1 − vc2
1 − vc2
L0
185
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
Für einen bewegten Beobachter lautet die Energiebilanz:
E ∗ (v) = E(v) + L+ + L−
= E(v) +
1 + vc + 1 − vc
q
L0
2
1 − vc2
2L0
⇒ E ∗ (v) − E(v) = q
2
1 − vc2
wir subtrahieren E0∗ − E0 = 2L0


1
⇒ (E ∗ (v) − E0∗ ) − (E(v) − E0 ) = 2L0  q
{z
} |
{z
}
|
1−
∗ (v)
Ekin
Ekin (v)
v2
c2
− 1
∗ (v) . . . kinetische Energie des angeregten Atoms
Ekin
Ekin (v) . . . kinetische Energie des Atoms im Grundzustand


∗
(v) − Ekin (v) = 2L0  q
Ekin
1
1−
v2
c2
− 1
⇒ Die kinetische Energie ändert sich durch Emission der Photonen, trotz verschwindendem Impulsübertrag.
Für
v
c
1 gilt:
1
Ekin ≈ m0 v 2
2
1
∗
Ekin
≈ m∗0 v 2
2
1
q
1−
v2
c2
≈1+
1 v2
2 c2
damit
1 v2
1 2 ∗
v (m0 − m0 ) = 2L0 ·
2 | {z }
2 c2
∆m
186
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
∆m =
E0∗ − E0
∆E0
2L0
=
= 2
2
2
c
c
c
Interpretation als:
E0 = m0 c2
. . . Energieinhalt des ruhenden Systems
vorhin
2L0
m∗0 c2 − m0 c2
q
E ∗ (v) − E(v) = q
=
2
↑
v2
1 − c2 2L0 = ∆mc2 1 − vc2
m∗ c2
⇒ E ∗ (v) = q 0
2
1 − vc2
m0 c2
E(v) = q
2
1 − vc2
Taylorentwicklung:
1
q
1−
v2
c2
=1+
1 v2 3 v4
+
+σ
2 c2
8 c4
v6
c6
3
v4
1
E(v) = m0 c2 + m0 v 2 + m0 2 + . . .
2
8
c
m0 c2 . . . Ruheenergie
1
2
2 m0 v . . .
v4
0 c2
3
8m
nichtrelativistische kinetische Energie
+ . . . . . . relativistische Korrekturen
187
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
5.3.2 Geschwindigkeitsabhängigkeit der trägen Masse
m0 c2
vorhin: E(v) = q
= m(v)c2
v2
1 − c2
m0
mit m(v) := q
1−
v2
c2
Ist die Interpretation von m(v) als geschwindigkeitsabhängige träge Masse sinnvoll?
dE = dW = F dx =
↑
↑
IV.1
F =
E = mc2 =
k
p
v
⇒ EdE = c2
dp
dx
dx = dp
= dp · v
dt
dt
dp
dt
p 2
c
v
(∗) | · dE (= dp · v)
p
· vdp = c2 pdp
v
Integration liefert
E 2 = c2 p2 + E02
E0 . . . Integrationskonstante
mit p =
Ev
c2
(∗)
⇒ E2 =
E 2v2
+ E02
c2
v2
E 2 1 − 2 = E02
c
E0
d.h. E(v) = q
k
1−
2
mc
v2
c2
E0
2
⇒ m(v) = q c
1−
188
v2
c2
Prof. Dr. habil. Wolf Gero Schmidt
Universität Paderborn, Lehrstuhl für Theoretische Physik
speziell m(v = 0) = m0 =
E0
:
c2
geschwindigkeitsabhängige, träge Masse
m0
m(v) = q
1−
189
v2
c2