Magnetfeld eines Dipols

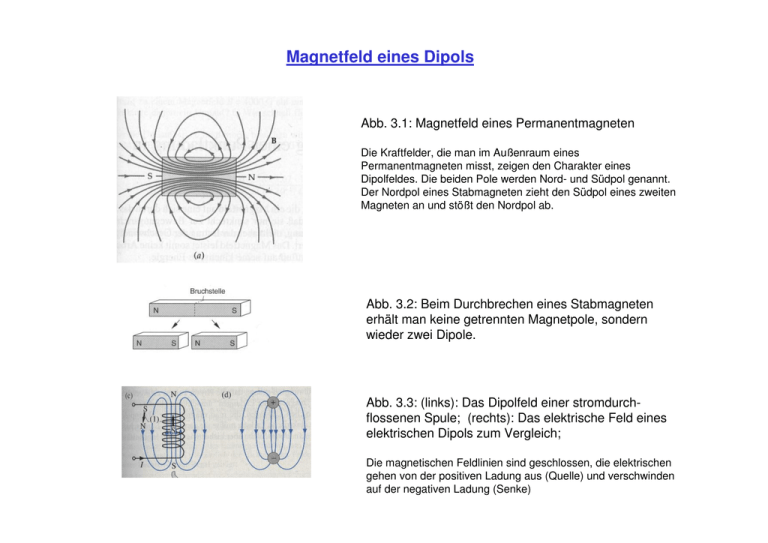
Magnetfeld eines Dipols
Abb. 3.1: Magnetfeld eines Permanentmagneten
Die Kraftfelder, die man im Außenraum eines
Permanentmagneten misst, zeigen den Charakter eines
Dipolfeldes. Die beiden Pole werden Nord- und Südpol genannt.
Der Nordpol eines Stabmagneten zieht den Südpol eines zweiten
Magneten an und stößt den Nordpol ab.
Abb. 3.2: Beim Durchbrechen eines Stabmagneten
erhält man keine getrennten Magnetpole, sondern
wieder zwei Dipole.
Abb. 3.3: (links): Das Dipolfeld einer stromdurchflossenen Spule; (rechts): Das elektrische Feld eines
elektrischen Dipols zum Vergleich;
Die magnetischen Feldlinien sind geschlossen, die elektrischen
gehen von der positiven Ladung aus (Quelle) und verschwinden
auf der negativen Ladung (Senke)
Magnetfelder eines geraden Leiters und einer Spule
Abb. 3.4: Magnetfeldlinien um einen geraden stromdurchflossenen Draht. Die Feldstärke
fällt mit 1/r ab.
Abb. 3.5. Magnetfeld einer
stromdurchflossenen langen Zylinderspule
Beispiele für die Berechnung von Magnetfeldern
Abb. 3.6: B-Feld Berechnung, Beispiel: gerader Leiter
(a)
(b)
Integrationsweg entlang der kreisförmigen Magnetfeldlinien;
Feldstärke | B(r) | als Funktion des Abstandes r von der
Drahtmitte.
Abb. 3.7: B-Feld Berechnung, Beispiel: leitendes Rohr
Auch für einen Leiter, der sich von einem Draht zu einem Rohr
aufweitet, ist das Magnetfeld kreissymmetrisch. Im Außenraum, für
r > ra nimmt das Magnetfeld von der Aufweitung des Leiters keine
Notiz und liegt mit gleicher Stärke vor wie bei einem dünnen
geraden Leiter. Im Innern des Rohrs dagegen erzeugt der Strom
kein Magnetfeld.
Abb. 3.8: B-Feld Berechnung, Beispiel: Spule
Integrationsweg zur Bestimmung des Magnetfeldes einer langen
Zylinderspule.
Magnetische Kräfte auf Ladungen
Abb. 3.9: Illustration der Lorentz-Kraft
Abb. 3.10: Magnetische Kräfte zwischen
zwei Leitern sind anziehend bei paralleler
(gestrichelt) und abstoßend (volle Linie) bei
entgegengesetzter Stromrichtung.
Fadenstrahlrohr: e/m Bestimmung des Elektrons
Abb. 3.11: Fadenstrahlrohr
Links: Experimenteller Aufbau: Von zwei Spulen, deren Abstand gleich dem Radius ist (Helmholtz-Spulen) wird
im Bereich des Zentrums ein praktisch homogenes Magnetfeld erzeugt. Elektronen, die aus einer Glühkathode
austreten und anschließend eine elektrostatische Beschleunigungsstrecke durchlaufen, werden aufgrund der
wirkenden Lorentz-Kraft auf eine Kreisbahn gezwungen.
Rechts: Prinzipskizze zur Demonstration der Lorentz-Kraft und zur Berechnung der Bahn eines Elektrons im
Vakuum. Das B-Feld steht senkrecht zur Zeichenebene.
Kraft auf eine Leiterschleife im Magnetfeld
Abb. 3.12: Kraft auf eine Leiterschleife im Magnetfeld
Links: Kräfte, die auf eine stromdurchflossene, rechteckige Leiterschleife wirken, wenn sich diese in einem
homogenen Magnetfeld B befindet, das parallel zur Schleifenebene liegt. Durch die Kräfte entsteht ein
Drehmoment, das versucht, die Schleife so zu drehen, dass ihre Ebene senkrecht zum Magnetfeld steht.
Rechts: Die Orientierung der Leiterschleife wird durch den Flächennormalenvektor beschrieben. Mit Hilfe der
Rechte-Hand-Regel lässt sich die Orientierung von n ermitteln: zeigen die Finger in Richtung des Stroms, so gibt
die Richtung des Daumens die Richtung von n an.
Hall –Effekt
Abb. 3.13: Der Hall Effekt
Das Magnetfeld zeigt in die Papierebene hinein. Sowohl auf positive Ladungsträger, die sich von rechts nach links
bewegen, als auch auf negative Ladungsträger, die sich von links nach rechts bewegen, übt das Magnetfeld eine
nach unten gerichtete Kraft aus. Es resultiert im Leiter eine elektrische Spannung, die sog. Hall-Spannung.