6. ¨Ubung (KW 26/27)

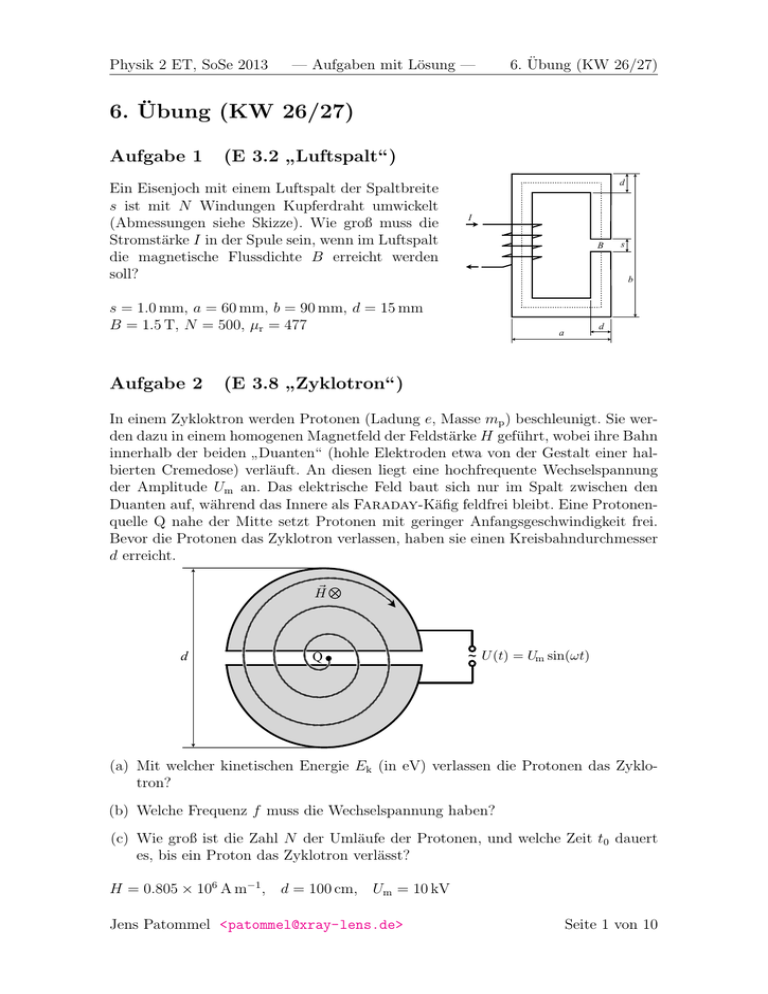
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
6. Übung (KW 26/27)
Aufgabe 1
(E 3.2 Luftspalt“)
”
Ein Eisenjoch mit einem Luftspalt der Spaltbreite
s ist mit N Windungen Kupferdraht umwickelt
(Abmessungen siehe Skizze). Wie groß muss die
Stromstärke I in der Spule sein, wenn im Luftspalt
die magnetische Flussdichte B erreicht werden
soll?
d
I
B
b
s = 1.0 mm, a = 60 mm, b = 90 mm, d = 15 mm
B = 1.5 T, N = 500, µr = 477
Aufgabe 2
s
d
a
(E 3.8 Zyklotron“)
”
In einem Zykloktron werden Protonen (Ladung e, Masse mp ) beschleunigt. Sie werden dazu in einem homogenen Magnetfeld der Feldstärke H geführt, wobei ihre Bahn
innerhalb der beiden Duanten“ (hohle Elektroden etwa von der Gestalt einer hal”
bierten Cremedose) verläuft. An diesen liegt eine hochfrequente Wechselspannung
der Amplitude Um an. Das elektrische Feld baut sich nur im Spalt zwischen den
Duanten auf, während das Innere als Faraday-Käfig feldfrei bleibt. Eine Protonenquelle Q nahe der Mitte setzt Protonen mit geringer Anfangsgeschwindigkeit frei.
Bevor die Protonen das Zyklotron verlassen, haben sie einen Kreisbahndurchmesser
d erreicht.
�
H
d
Q
~ U (t) = Um sin(ωt)
(a) Mit welcher kinetischen Energie Ek (in eV) verlassen die Protonen das Zyklotron?
(b) Welche Frequenz f muss die Wechselspannung haben?
(c) Wie groß ist die Zahl N der Umläufe der Protonen, und welche Zeit t0 dauert
es, bis ein Proton das Zyklotron verlässt?
H = 0.805 × 106 A m−1 , d = 100 cm, Um = 10 kV
Jens Patommel <[email protected]>
Seite 1 von 10
Physik 2 ET, SoSe 2013
Aufgabe 3
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
(E 4.11 Leiterrechteck“)
”
Gegeben ist ein Leitersystem gemäß Skizze.
b
d
(a) Durch den Leiter L2 fließt ein Strom der Stärke
I2 . Wie groß ist der magnetische Fluss Φ1
durch die Rechteckfläche, die der Leiter L1 umrandet?
(b) Durch L2 fließt sinusförmiger Wechselstrom
(Stromstärke I2,eff , Frequenz f ). Wie groß ist
die induzierte Spannung U1,eff im Leiter L1 ?
a
(c) Der Leiter L1 hat den Widerstand R. Wie groß
ist die Stromstärke I1,eff ?
(d) Welche Leistung P wird im Leiter L1 in
Wärme umgesetzt, und woher stammt die verbrauchte Energie?
L1
L2
I2 = 10 A, I2,eff = 10 A, f = 50 Hz, R = 0.10 Ω, a = 100 cm, b = 10 cm, d = 2.0 cm
Aufgabe 4
(E 4.5 Rotierende Spule“)
”
Durch eine lange Spule (Länge l1 , Windungszahl N1 ) fließt ein Strom mit der
Stromstärke I1 . In dieser Spule rotiert eine zweite Spule (Windungszahl N2 , Windungsfläche A2 ) mit der Frequenz f2 . Berechnen Sie den Maximalwert Um der entstehenden Wechselspannung!
l1 = 20 cm, N1 = 1000, I1 = 50 A, N2 = 400, A2 = 6.0 cm2 , f2 = 100 s−1
Jens Patommel <[email protected]>
Seite 2 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Lösung zu Aufgabe 1
~ r), welche mit der magnetischen
Die Spule erzeugt eine magnetische Feldstärke H(~
~ r) über die Materialgleichung
Flussdichte B(~
~ r) = µr (~r)µ0 H(~
~ r)
B(~
verknüpt ist. Innerhalb des Eisenjochs hat die relative Permeabilität den Wert µrE ,
im Luftspalt hingegen den Wert µrL , d. h.
(
µrE , ~r ∈ Eisenjoch
µr (~r) =
.
µrL , ~r ∈ Luftspalt
Die magnetische Flussdichte ist im Innern des Eisenjochs überall parallel zur Mittellinie gerichtet und hat den konstanten Betrag BE . Wenn die Größe des Luftspalts s
hinreichend klein im Vergleich zum Durchmesser d des Eisenjochs ist, so bleiben die
Flusslinien auch innerhalb des Spaltes parallel zueinander, so dass die magnetische
Flussdichte im Spalt den konstanten Betrag BL hat, wobei
BL = BE =: B
gilt. Die magnetische Flussdichte hat überall im Eisenjoch und im Luftspalt den
konstanten Wert B. Somit folgt für die magnetischen Feldstärken im Eisenjoch und
im Luftspalt der Zusammenhang
µrE µ0 HE = BrE = B = BrL = µrL µ0 HL
1
B
(1.1)
=⇒ HE =
µrE µ0
1
HL =
B.
(1.2)
µrL µ0
Die magnetische Feldstärke hat die Eigenschaft, dass ein geschlossenes Wegintegral
dem elektrischen Gesamtstrom entspricht, der durch die vom Weg definierte Querschnittsfläche fließt,
I
~ r) .
Iges = d~r H(~
Wählt man als Integrationsweg die in der Abbildung gestrichtelt dargestellte Linie, so wird jede Spulenwindung genau einmal umrundet, so dass der umschlossene
elektrische Gesamtstrom Iges = N I beträgt und sich folgendes Integral ergibt:
I
Z
Z
Z
Z
~ r)
d~
r kH(~
~
~
~
N I = Iges = d~r H(~r) = d~r H(~r) + d~r H(~r) =
drH(~r) + drH(~r)
Eisen
Z
Z
= HE dr + HL
WEisen
Eisen
Luft
Luft
i
h
dr = HE (b − d) + (b − d − s) + (a − d) + (a − d) + HL s
| {z } | {z } | {z } | {z }
WLuft
links
rechts
oben
unten
= HE [2(a + b − 2d) − s] + HL s
1
1
(1.1)
=
B [2(a + b − 2d) − s] +
Bs
(1.2) µrE µ0
µrL µ0
Jens Patommel <[email protected]>
Seite 3 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Nach der gesuchten Stromstärke aufgelöst finden wir folgendes Ergebnis:
s
B 2(a + b − 2d) − s
+
I=
N µ0
µrE
µ
rL
1.5 T
2(60 + 90 − 2 · 15) − 1.0 1.0
=
+
mm
500 · 4π · 10−7 V s A−1 m−1
477
1
T A m2
T m2
= 3.58
= 3.58 A
= 3.58 A .
Vs
Vs
Lösung zu Aufgabe 2
(a) Bis auf den kleinen Spalt zwischen den beiden Duanten wirkt auf die Protonen
ausschließlich die von der magnetischen Flussdichte hervorgerufene Lorentzkraft,
deren Richtung stets senkrecht zur momentanen Bewegungsrichtung zeigt und deren
Betrag
FL = evB
lautet. Offenkundig ist der Betrag der Lorentzkraft konstant, solange der Geschwindigkeitsbetrag v und der Betrag der magnetischen Flussdichte konstant sind.
Innerhalb der Duanten ist das Magnetfeld räumlich homogen und zeitlich konstant,
so dass sich der Betrag der Lorentzkraft nur dann ändert, wenn sich der Betrag
der Geschwindigkeit ändert. Der Geschwindigkeitsbetrag kann sich allerdings nur
dann ändern, wenn es eine Kraftkomponente in Bewegungsrichtung des Teilchens
gibt, was bei der Lorentzkraft nicht der Fall ist, denn diese wirkt stets senkrecht
zur Bewegungsrichtung. Folglich bleibt die radial beschleunigende Kraft FL zeitlich
konstant und das Proton bewegt sich innerhalb der Duanten auf einer Kreisbahn
vom Radius r, wobei die Radialbeschleunigung
ar =
v2
r
beträgt. Da diese Beschleunigung von der Lorentzkraft verursacht wird, gilt nach
dem zweiten Newtonschen Gesetz
FL = mp ar
und folglich
v2
evB = mp
r
⇐⇒
v=
e
µ0 H r .
mp
(2.1)
Geschwindigkeitsbetrag und Bahnradius sind also proportional zueinander, wobei
die Proportionalitätskonstante ausschließlich von der spezifischen Ladung e/mp des
Protons und von der Stärke des Magnetfeldes abhängt. Mit dem Betrag der Geschwindigkeit kann man nun zu jedem Bahnradius die kinetische Energie des Protons berechnen, insbesondere für den Bahnradius d/2 unmittelbar vor Verlassen des
Jens Patommel <[email protected]>
Seite 4 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Zyklotrons:
Ek =
1
m v2
2 p
=
1
m
2 p
e
d
µ0 H
mp
2
2
=
e2 d2 µ20 H 2
8mp
(2.2)
2
e · 1.602 × 10−19 C · (1.00 m · 4π · 10−7 V s A−1 m−1 · 0.805 × 106 A m−1 )
8 × 1.67 × 10−27 kg
1.602 × 16π 2 × 0.8052
C V2 m−2 s2
=
· 10−19−2·7+2·6+27 · e ·
8 × 1.67
kg
CV
}J
= 12.27 × 106 · e|{z}
· V·
2 −2 }J
kg m s
=
eV
= 12.27 MeV .
(b) In Teilaufgabe (a) haben wir festgestellt, dass die Bahngeschwindigkeit proportional zum Bahnradius ist. Daraus folgt sofort, dass die Umlaufdauer T des Protons
vom Bahnradius r unabhängig ist, d. h. die Zeitdauer für eine vollständige Kreisbahn ist immer gleich groß, egal wie schnell das Proton fliegt und welchen Abstand
es vom Kreismittelpunkt hat. Die (konstante) Umlaufdauer berechnen wir zu
T =
u (2.1)
Kreisumfang
=
=
Bahngeschwindigkeit
v
2πr
e
µ Hr
mp 0
=
2π
(2.3)
e
µH
mp 0
Die Umlauffrequenz f ist definiert als als Anzahl der Umläufe pro Zeitintervall, sie
ergibt sich also als Kehrwert der Umlaufdauer:
e µ0
H
mp 2π
1.602 × 10−19 C
=
· 2 × 10−7 V s A−1 m−1 · 0.805 × 106 A m−1
1.67 × 10−27 kg
VCs
2 · 1.602 · 0.805
· 10−19−7+6+27 ·
=
1.67
kg m2
VC
= 1.54 × 107 ·
· s−1
kg m2 s−2
J
= 1.54 × 107 ·
· s−1 = 15.4 MHz .
Nm
(2.3)
f = T −1 =
Die Umlauffrequenz des Protons betträgt – unabhängig von seinem Radius und
seinem Geschwindigkeitsbetrag – 15.4 MHz.
Man mache sich klar, was passsieren würde, wenn an den Duanten eine Gleichspannung anläge. Dann erführe das Proton im linken Spalt zwischen den Duanten eine in
Bewegungsrichtung orientierte und im rechten Spalt eine entgegen der Bewegungsrichtung orientierte Beschleunigung (oder umgekehrt), die beiden Beschleunigungen
höben sich also gerade auf, so dass das Proton nach jedem Umlauf dieselbe Geschwindigkeit hätte. Damit die Beschleunigung immer nur in Bewegungsrichtung
des Protons wirkt, muss das elektrische Feld im Spalt zwischen den Duanten nach
Jens Patommel <[email protected]>
Seite 5 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
jedem halben Umlauf des Protons umorientiert werden, folglich muss an den Duanten eine Wechselspannung anliegen, und zwar mit derselben Frequenz, mit der das
Proton im Zyklotron umläuft. Man nennt diese Frequenz auch Zyklotronfrequenz.
(c) Wie viele Umläufe braucht das Proton bis zum Verlassen des Zyklotrons? In
Teilaufgabe (a) wurde die kinetische Energie ermittelt, die das Proton beim Verlassen des Zyklotrons hat. Woher stammt diese Energie? Sicher nicht vom Magnetfeld,
denn die von ihm verursachte Lorentzkraft wirkt immer nur senkrecht zur Bewegungsrichtung und kann somit keine Energie auf das Proton übertragen. Einzig das
elektrische Feld überträgt Energie auf das Proton, und zwar jedes Mal, wenn das
Proton den Spalt durchquert. Wenn wir annehmen, dass die Freqeunz der Wechselspannung der Zyklotronfrequenz entspricht und die Wechselspanung ihr Maximum
erreicht, wenn sich das Proton gerade im Spalt befindet, dann erhöht sich die kinetische Energie des Protons pro Spaltdurchlauf um
∆E = eUm .
(2.4)
Pro Umlauf durchfliegt das Proton zweimal den Spalt, folglich beträgt die Anzahl
der Umläufe bis zum Verlassen des Zyklotron
N=
12.27 MeV
12.27 × 106 eV
Ek (2.4) Ek
=
=
=
= 614 .
2∆E
2eUm
2e · 10 kV
20 × 103 eV
Insgesamt wird dafür die Zeit
t0 = N T =
N
614
=
= 39.8 × 10−6 s = 40 µs
f
15.4 MHz
benötigt.
Jens Patommel <[email protected]>
Seite 6 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Lösung zu Aufgabe 3
(a) Der magnetische Fluss durch die vom Leiter L1 umrandete Fläche A ergibt sich
aus folgendem Integral:
Z
Z
Z
~ H
~
dAk
~
~
~
~
Φ1 = dAB(~r) = µ0 dAH(~r) = µ0 dAH(~r) .
(3.1)
A
A
Dieses Flächenintegral lässt sich als Ineinandergeschachtelte Riemannintegrale
über zwei Koordinaden schreiben. Bei der
Wahl des Koordinatensystems hat man
freie Hand, man könnte zum Beispiel kartesische Koodinaten oder Polarkoordinaten wählen. Weil die Fläche A rechteckig
ist, liegt es Nahe, ein kartesisches Koordinatensystem zu nehmen, dessen Achsen
parallel zu den Seiten des Rechtecks verlaufen. Legen wir also die x-Achse horizontal, die y-Achse vertikal und den Koordinatenursprung auf den Leiter L2 (siehe Zeichnung), dann kann man Gleichug
(3.1) wie folgt umschreiben:
Z
(3.1)
Φ1 = µ0
A
d+b
Z
A
y
a
A
dA
dy
dx
x
d
d+b
Zd+b
Zd+b Za
Zd+b Za
I2 a
I2
= µ0 dx
y
dAH(~r) = µ0 dx dyH(x, y) = µ0 dx dy
2πx
2πx 0
= µ0 dx
d
0
d
0
d
d+b
µ0
µ0
I2 a
=
I2 a log |x| d =
I2 a log(1 + db )
2πx
2π
2π
(3.2)
d
= 2 × 10−7 V s A−1 m−1 · 10 A · 1 m · log(1 +
10
)
2
= 3.58 × 10−6 V s = 3.58 µWb .
(b) Im Leiter L2 fließt nun kein Gleichstrom mehr, sondern Wechselstrom der Form
√
I2 (t) = I2,m sin(2πf t) = I2,eff 2 sin(2πf t) .
(3.3)
√
Der Faktor 2 zwischen Effektiv- und Maximalstromstärke sowie zwischen Effektivund Maximalspannung ergibt sich aus der Forderung
Ueff Ieff
ZT
ZT
ZT
1
1
1
= hP iT =
dtP (t) =
dtU (t)I(t) =
dt Um sin(2πf t) Im sin(2πf t)
T
T
T
0
0
0
T
Um Im
1
f T =1 1
=
t−
sin(2πf t) cos(2πf t)
= √2 Um √12 Im ,
2T
2πf
0
!
Jens Patommel <[email protected]>
Seite 7 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
d. h. die Effektivwerte Ueff und Ieff geben an, wie stark ein Gleichstrom mit diesen
Effektivwerten sein müsste, damit dieser die gleiche mittlere Leistung erbringt wie
der vorliegende Wechselstrom mit den Maximalwerten Um und Im .
Der Wechselstrom verursacht in der Leiterschleife L1 einen zeitlich veränderlichen
magnetischen Fluss, den wir mit den Gleichungen (3.2) und (3.3) berechnen:
√
µ0
(3.3) µ0
a log(1 + db ) I2 (t) =
a log(1 + db ) I2,eff 2 sin(2πf t)
2π
|2π
{z
}
= Φm sin(2πf t) .
Φm
(3.2)
Φ(t) =
(3.4)
Das zeitlich veränderliche Magnetfeld induziert in der Leiterschleife eine Spannung,
die sich aus der Zeitableitung des magnetischen Flusses ergibt:
(3.4)
d
U1 (t) = −Φ̇(t) = − dt
Φm sin(2πf t) = − 2πf Φm cos(2πf t) = −U1,m cos(2πf t) .
| {z }
U1,m
(3.5)
Damit errechnen wir eine induzierte effektive Spannung von
√
U1,m
2π
(3.4) 2π µ0
af log(1 + db ) I2,eff 2 = µ0 af I2,eff log(1 + db )
U1,eff = √ = √ f Φm = √
2
2
2 2π
−7
−1
−1
= 4π · 10 V s A m · 1 m · 50 s−1 · 10 A · ln 6 = 1.13 mV .
(c) Die effektive Stromstärke I1,eff , die von der effevtiven induzierten Spannung
verursacht wird, hat den Wert
I1,eff =
1.13 mV
U1,eff
=
= 11.3 mA .
R
0.10 Ω
(d) Der Mittelwert der in Wärme umgesetzten Leistung beträgt
P = U1,eff I1,eff = 1.13 mV · 11.3 mA = 12.8 µW .
Die Energie stammt von der Spannungsquelle, die den Leiter L2 mit Wechselstrom
versorgt.
Jens Patommel <[email protected]>
Seite 8 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Lösung zu Aufgabe 4
I1 N1
~
dA
↵(t)
U2 (t)
~
B
A2
N2
senkrecht zur Zeichenebene
verlaufende Rotationsachse
l1
Die in der Sekundärspule induzierte Spannung ergibt sich aus der Zeitableitung des
magnetischen Flusses, der die Querschnittsfläche der Sekundärspule durchströmt“,
”
wobei es zu beachten gilt, dass jede der N2 Windungen additiv zur Gesamptspannung
beiträgt:
U2 (t) = −N2 Φ̇(t) .
(4.1)
Der magnetische Fluss wird berechnet, indem man die von der Primärspule erzeugte magnetische Flussdichte über der Querschnittsfläche A2 der Sekundärspule
integriert. Bezeichnet man den senkrecht auf dem Flächenelement stehenden Vektor
~ und den zeitabhängigen Winkel zwischen diesem Vektor
vom Betrage dA mit dA
und der magnetischen Flussdichte mit α(t) (siehe Zeichnung), so ergibt sich folgender
Ausdruck für den magnetischen Fluss:
x
x
x
~ B(~
~ r) = dAB(~r) cos α(t) = B cos α(t) dA = A2 B cos α(t) . (4.2)
Φ(t) = dA
A2
A2
A2
Hierbei wurde ausgenutzt, dass das Magnetfeld im Innern einer langen Spule räumlich homogen ist und überall parallel zur Spulenachse verläuft, so dass der von ~r
~ vor das Integral gezogen werden darf. Gleichung (4.2)
unabhängige Betrag B = |B|
setzen wir in (4.1) ein und erhalten unter Beachtung der Kettenregel
(4.1)
(4.2)
d
[A2 B cos α(t)] = N2 A2 B α̇(t) sin α(t) .
U2 (t) = −N2 Φ̇(t) = −N2 dt
(4.3)
Den Betrag B der räumlich homogenen und zeitlich konstanten magnetischen Flussdichte ermittelt man anhand der von der Primärspule erzeugten magnetischen Feldstärke zu
B = µ0 H = µ0
N1
I1 ,
l1
(4.4)
was sogleich in (4.3) eingesetzt wird:
(4.3)
(4.4)
U2 (t) = N2 A2 B α̇(t) sin α(t) = N2 A2 µ0
Jens Patommel <[email protected]>
N1
I1 α̇(t) sin α(t) .
l1
(4.5)
Seite 9 von 10
Physik 2 ET, SoSe 2013
— Aufgaben mit Lösung —
6. Übung (KW 26/27)
Kümmern wir uns jetzt um die Winkel-Zeit-Funktion α(t)! Wenn wir annehmen,
dass die Sekundärspule mit konstanter Frequenz f2 und somit mit konstanter Winkelgeschwindigkeit ω2 = 2πf2 um eine zur Längsachse der Primärspule senkrecht
stehende Rotationsachse rotiert, so gilt für den Winkel α(t) und dessen Zeitableitung α̇(t):
α(t) = α0 + ω2 t = α0 + 2πf2 t ,
α̇(t) = ω2 = 2πf2 .
(4.6)
(4.7)
Ineinander eingesetzt erhalten wir die in der Sekundärspule induzierte Wechselspannung
(4.5)
U2 (t) = N2 A2 µ0
N1
(4.6)
I1 α̇(t) sin α(t) = 2πf2 µ0 N1 N2 A2 I1 l1−1 sin(α0 + 2πf2 t)
(4.7) |
{z
}
l1
Um
mit einer maximalen Amplitude von
Um = 2πµ0 f2 N1 N2 A2 I1 l1−1
= 8π 2 × 10−7 V s A−1 m−1 · 100 s−1 · 400 000 · 6.0 × 10−4 m2 · 50 A · (0.2 m)−1
= 47.4 V .
Quellen
Die Aufgaben 3, 4 und 5 sind entnommen aus: Peter Müller, Hilmar Heinemann,
Heinz Krämer, Hellmut Zimmer, Übungsbuch Physik, Hanser Fachbuch, ISBN: 9783-446-41785-4
http://www.hanser-fachbuch.de/buch/Uebungsbuch+Physik/9783446417854
Die Übungs- und Lösungsblätter gibt es unter
http://newton.phy.tu-dresden.de/~patommel/Physik_2_ET
Die Homepage zur Vorlesung findet sich unter
http://www.iapp.de/iapp/lehre/materialien/?v=pe
Jens Patommel <[email protected]>
10