Jahrgangsstufe 10 - Rhön

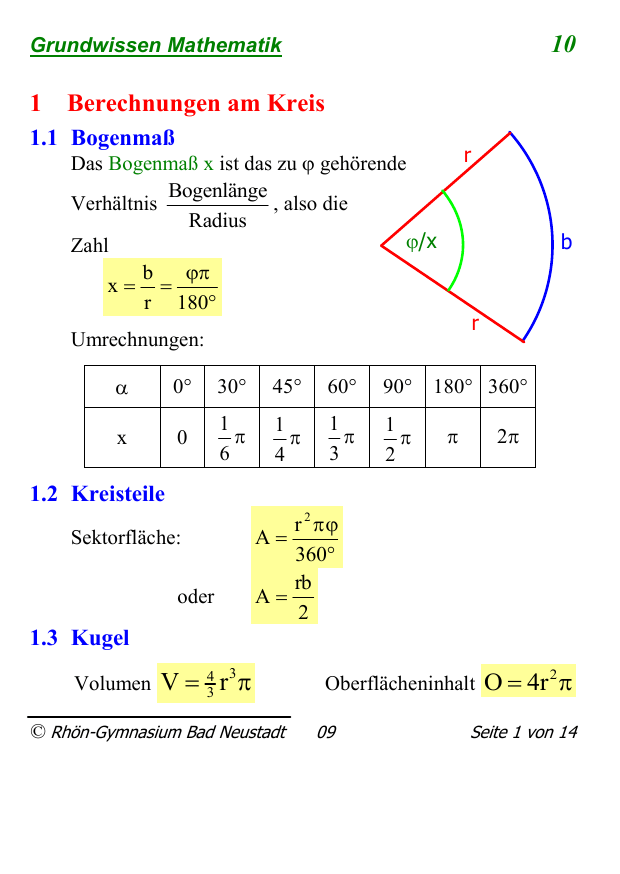
10
Grundwissen Mathematik
1
Berechnungen am Kreis
1.1 Bogenmaß
r
Das Bogenmaß x ist das zu  gehörende
Bogenlänge
Verhältnis
, also die
Radius
/x
Zahl

b
x 
r 180
b
r
Umrechnungen:

0°
30°
45°
60°
90° 180° 360°
x
0
1

6
1

4
1

3
1

2

2
1.2 Kreisteile
Sektorfläche:
oder
r 2 
360
rb
A
2
A
1.3 Kugel
Volumen
V  43 r 3
© Rhön-Gymnasium Bad Neustadt
Oberflächeninhalt O  4r 
2
09
Seite 1 von 14
10
Grundwissen Mathematik
2
Sinus, Kosinus und Tangens am Einheitskreis
-cos
tan

cos
Sinus, Kosinus und Tangens beliebiger
Winkel
Für die Vorzeichen gilt
Sinus
Kosinus Tangens
1
-sin
-sin
-1
sin
sin
1
-1
Für negative Winkel (im Uhrzeigersinn) gilt:
sin()   sin , cos()  cos , tan()   tan 
Bsp.:
sin150  sin(180 - 150 )  sin30 
1
2
tan 300   tan( 360  300 )   tan 60   3
sin 
1
2
2  1  45 und 2  180  45  135
© Rhön-Gymnasium Bad Neustadt
09
Seite 2 von 14
10
Grundwissen Mathematik
3
Trigonometrie am allgemeinen Dreieck
3.1 Sinussatz
In einem Dreieck verhalten sich die Längen zweier Seiten wie
die Sinuswerte der gegenüberliegenden Winkel.
a sin 
usw.

b sin 
3.2 Kosinussatz
In jedem Dreieck gilt
c2  a 2  b2  2abcos  usw.
Sonderfall: Satz des Pythagoras, falls der Winkel 90° hat.
Der Kosinussatz liefert den Winkel eindeutig, der Sinussatz nicht.
Bsp.: Das Dreieck mit a=6cm, b=4,5cm und =62° ist nach
SsW eindeutig. Aus dem Sinussatz ergibt sich
b  sin  4,5cm  sin62
sin  

 0,6622
a
6cm
 1  41,5 und  2  180  41,5  138,5
2 scheidet aus, weil im Dreieck der größeren Seite der größere Winkel gegenüberliegen muss. Die Überprüfung mit der
Innenwinkelsumme liefert dieselbe Entscheidung.
© Rhön-Gymnasium Bad Neustadt
09
Seite 3 von 14
10
Grundwissen Mathematik
4
Trigonometrische Funktionen
y
1
O
1
2
3
4
5
6 x
-1
Sinusfunktion f(x) = sin x mit Df = IR .
punktsymmetrisch zu (0/0); Periodenlänge 2Wf = [-1;1]
Kosinusfunktion f(x) = cos x mit Df = IR .
achsensymmetrisch zur y-Achse; Periodenlänge 2 Wf = [-1;1]
y
2
Tangensfunktion f(x) = tan x
mit Df = IR \ (2z  1) 2 
1
O
1
2
3 x
-1
punktsymmetrisch zu (0/0); Periodenlänge Wf = IR
-2
© Rhön-Gymnasium Bad Neustadt
09
Seite 4 von 14
10
Grundwissen Mathematik
Die allgemeine Sinusfunktion
f (x)  a sin[b(x  c)]  d mit a, b  0 Periode
2
b
a: Streckung oder Stauchung in y-Richtung
b: Streckung oder Stauchung in x-Richtung
c: Verschiebung nach rechts ( c < 0) oder links (c > 0)
d: Verschiebung nach oben (d > 0) oder unten (d < 0)
5
Exponentialfunktion
5.1 Exponentielles Wachstum
Ist die Änderung pro Zeiteinheit direkt proportional zum aktuellen Bestand, so liegt ein exponentielles Wachstum oder
eine exponentielle Abnahme vor. (x im Exponenten)
x
Wachstumsgesetz y  b  a
b: Anfangswert
a: Wachstumsfaktor oder Abnahmefaktor
a>1 exponentielle Zunahme,
0<a<1 exponentielle Abnahme
© Rhön-Gymnasium Bad Neustadt
09
Seite 5 von 14
10
Grundwissen Mathematik
5.2 Exponentialfunktionen
y  ax a  IR  , x  IR
 12 
x
 
1
10
+
W = IR
streng monoton steigend
für a>1
streng monoton fallend
für 0<a<1
Die Graphen von
y  a x und y   1a 
sind zueinander symmetrisch bzgl. der y-Achse.
x
y
4
10x
2x
3
2
x
6
1
-2
-1
O
1
2 x
Logarithmus
Ist b  IR  \ 1 und bx  a , so heißt der Exponent x der Logarithmus von a zur Basis b: x  logb a .
( log b a ist diejenige Zahl, mit der man b potenzieren muss,
um a zu erhalten.)
log b 1  0; l og b b  1
log b b x  x; blogb x  x
© Rhön-Gymnasium Bad Neustadt
09
Seite 6 von 14
10
Grundwissen Mathematik
6.1 Rechnen mit Logarithmen
log b (u  v)  log b u  log b v
log b (u : v)  log b u  log b v
log b u z  z  log b u
(b, u, v  IR  , b  1, z  IR)
2  logb x  3logb y  log b z  log b
1
1
logb b  4 logb a   4 logb a
2
2
a
log b x
Basisumrechnung: log a x 
log b a
logb
b
x2 y3
z
4

Zehnerlogarithmus: Schreibweise: lg x : log10 x
Praxis: Auf dem TR ist die Zehnerlogarithmus-Taste mit log
beschriftet!
Näherungsweises Berechnen von Logarithmen mit beliebiger
log 5
 2,3219
Basis auf dem TR z.B. log 2 5 
log 2
© Rhön-Gymnasium Bad Neustadt
09
Seite 7 von 14
10
Grundwissen Mathematik
6.2 Exponential- und Logarithmusgleichungen
Variable im Exponenten – Lösungsprinzip –
2 x  32 x 1 | logarithmieren
lg 2 x  lg 32 x 1
x lg 2  ( 2x  1 )lg 3 nach x auflösen
x lg 2  2x lg 3 - lg 3
x lg 2  2x lg 3   lg 3
x(lg 2  2 lg 3 )   lg 3
x
 lg 3
lg 2  2 lg 3
Variable im Logarithmus – Lösungsprinzip –
log 5 ( 2x  1 )  3 |delogarithmieren
53  2x  1
x  62
7
Ganzrationale Funktionen
Ein Term der Form
a n x n  a n 1x n 1  ...  a 2 x 2  a1x  a 0 mit a 0 ...a n  IR; a n  0
heißt Polynom n-ten Grades.
© Rhön-Gymnasium Bad Neustadt
09
Seite 8 von 14
10
Grundwissen Mathematik
Eine Funktion der Form
f : x a n x n  a n 1x n 1  ...x 2  a1x  a 0 mit a 0 ...a n  ;a n  0
mit Df 
heißt ganzrationale Funktion n-ten Grades.
7.1 Potenzfunktionen
Jede Funktion f(x) = xn mit Df = IR und n  IN heißt Potenzfunktion mit natürlichem Exponenten.
y
5
x4
y
x2
x5 x3
2
4
1
3
-2
2
-1
1
2 x
-1
1
-2
-2
-1 O
1
2 x
n gerade
Wf = IR 0
achsensymmetrisch zur y Achse
gemeinsam (–1|1), (0|0), (1|1)
© Rhön-Gymnasium Bad Neustadt
-3
n ungerade
Wf = IR
punktsymmetrisch zu (0|0)
gemeinsam (–1|–1), (0|0), (1|1)
09
Seite 9 von 14
10
Grundwissen Mathematik
7.2 Polynomdivision
6x : 3x  
3
6x 3  16x 2  7x  10 : 3x  2   2x 2  4x  5
(6x 3  4x 2 )
(3x  2)  2x 2
12x 2  7x
12x2 : 3x  
 12x 2  8x 
 15x  10
(15x  10)
usw.
0
7.3 Nullstellen
f ist eine ganzrationale Funktion n-ten Grades.
Dann hat sie höchstens n Nullstellen.
Ist x = a Nullstelle von f, so gilt f(x) = (x–a)·g(x) mit Grad
g(x) = n–1.
7.4 Grenzwert
Unterscheiden sich die Funktionswerte von f(x) für x   bzw.
x – beliebig wenig von der Zahl a, so konvergiert f(x) gegen
den Grenzwert a.
lim f (x)  a bzw. lim f (x)  a
x 
x 
© Rhön-Gymnasium Bad Neustadt
09
Seite 10 von 14
10
Grundwissen Mathematik
7.5 Felder abstreichen
f(x) = x3 – x = x(x+1)(x–1)
NST x1 = –1, x2 = 0, x3 = 1
–1 0 1
x
– – + +
x+1 – + + +
x-1 – – – +
f(x) – + – +
y
3
2
f(x)
1
-2
7.6 Symmetrie
f(-x)
f(-x) = –f(x)
Graph punktsymmetrisch
zu (0|0).
-1
O
1
x
-1
-2
-3
y
2
f(-x)
-2
f(x)
1
-1
O
1
f(-x) = f(x)
Graph achsensymmetrisch
zur y-Achse
x
© Rhön-Gymnasium Bad Neustadt
09
Seite 11 von 14
10
Grundwissen Mathematik
8
Zusammengesetzte Zufallsexperimente
8.1 Bedingte Wahrscheinlichkeit
heißt für P(B)  0 die bedingte WahrP(A  B)
scheinlichkeit von A unter der Bedingung
P(B)
B.
oder Wahrscheinlichkeit von A unter der Bedingung, dass B eingetreten ist, oder Wahrscheinlichkeit von A im Ergebnisraum B.
PB (A) 
Bsp.: Bei einer Befragung von 80 Personen geben 65 an Englisch
und 55 Französisch zu sprechen. Von denen die Englisch sprechen, sprechen 45 auch Französisch.
PE (F) 
P(E) 
65
80
45
65
P(E  F)
  P(F) 
E
F
P(E  F)
PE (F)
F
P(E  F)
PE (F)
F
P(E  F)
PE (F) 
15
P(E) 
80
F
20
65
55
80
E
© Rhön-Gymnasium Bad Neustadt
09
Seite 12 von 14
10
Grundwissen Mathematik
55 65 45 10
 

80 80 65 80
Mit welcher Wahrscheinlichkeit spricht unter denen, die kein
Englisch sprechen, jemand Französisch?
10
P(E  F) 80 10
;
PE (F) 


15 15
P(E)
80
Mit welcher Wahrscheinlichkeit spricht unter denen, die kein
Englisch sprechen, jemand auch kein Französisch?
10 5
PE (F)  1  
15 15
5
P(„keine der beiden Sprachen“) = P(E  F)  P(E)  PE (F) 
80
Mit welcher Wahrscheinlichkeit spricht unter denen, die Französisch sprechen, jemand auch Englisch?
65 45

P(E  F) 80 65 45
PF (E) 


55
P(F)
55
80
a) P(„nur F“) = P(E  F)  P(F)  P(E  F) 
b)
c)
d)
e)
Lösung der Aufgaben mit der Vierfeldertafel
(Nur anwendbar bei zwei Ereignissen)
© Rhön-Gymnasium Bad Neustadt
09
Seite 13 von 14
10
Grundwissen Mathematik
8.2 Vierfeldertafel
Vierfeldertafel mit der absoluten Häufigkeit.
+
E E Gesamt
F
45 10
55
20
5
25
F
Gesamt 65 15
80
a) 10 sprechen nur Französisch. P(„nur F“) =
10
80
10
15
5
c) PE (F) 
15
b) PE (F) 
d) P(E  F) 
5
80
45
55
Vierfeldertafel mit der Wahrscheinlichkeit.
+
E E Gesamt
e) PF (E) 
F
45
80
10
80
55
80
F
20
80
5
80
25
80
Gesamt
65
80
15
80
1
© Rhön-Gymnasium Bad Neustadt
09
Seite 14 von 14