Nach oben

10
Grundwissen Mathematik
1
Berechnungen am Kreis
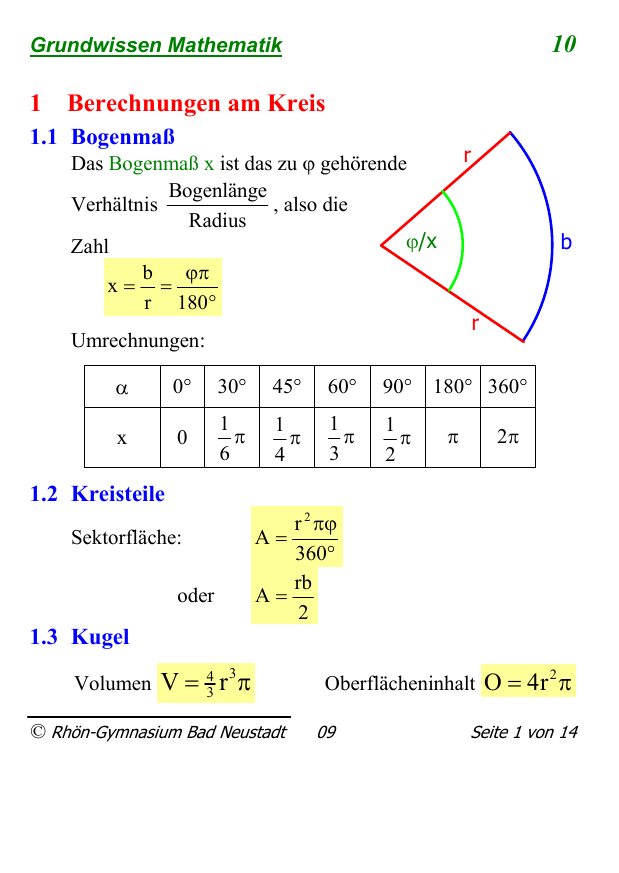
1.1 Bogenmaß
r
Das Bogenmaß x ist das zu ϕ gehörende
Bogenlänge
Verhältnis
, also die
Radius
ϕ/x
Zahl
b
ϕπ
x= =
r 180°
b
r
Umrechnungen:
α
0°
30°
45°
60°
90° 180° 360°
x
0
1
π
6
1
π
4
1
π
3
1
π
2
π
2π
1.2 Kreisteile
Sektorfläche:
oder
r 2 πϕ
360°
rb
A=
2
A=
1.3 Kugel
Volumen
V = 43 r 3π
© Rhön-Gymnasium Bad Neustadt
Oberflächeninhalt O = 4r π
2
09
Seite 1 von 14
10
Grundwissen Mathematik
2
Sinus, Kosinus und Tangens am Einheitskreis
-cosα
tanα
α
cosα
Sinus, Kosinus und Tangens beliebiger
Winkel
Für die Vorzeichen gilt
Sinus
Kosinus Tangens
1
-sinα
-sinα
-1
sinα
sinα
1
-1
Für negative Winkel (im Uhrzeigersinn) gilt:
sin( −α) = − sin α, cos( −α) = cos α, tan( −α) = − tan α
Bsp.:
sin150° = sin(180° - 150° ) = sin30° =
1
2
tan 300° = − tan( 360° − 300° ) = − tan 60° = − 3
sin α =
1
2
2 ⇒ α1 = 45° und α 2 = 180° − 45° = 135°
© Rhön-Gymnasium Bad Neustadt
09
Seite 2 von 14
10
Grundwissen Mathematik
3
Trigonometrie am allgemeinen Dreieck
3.1 Sinussatz
In einem Dreieck verhalten sich die Längen zweier Seiten wie
die Sinuswerte der zugehörigen Winkel.
a sin α
=
usw.
b sin β
3.2 Kosinussatz
In jedem Dreieck gilt
c 2 = a 2 + b 2 − 2ab cos γ usw.
Sonderfall: Satz des Pythagoras, falls der Winkel 90° hat.
Der Kosinussatz liefert den Winkel eindeutig, der Sinussatz nicht.
Bsp.: Das Dreieck mit a=6cm, b=4,5cm und α=62° ist nach
SsW eindeutig. Aus dem Sinussatz ergibt sich
b ⋅ sin α 4,5cm ⋅ sin62°
sin β =
=
≈ 0,6622
a
6cm
⇒ β1 = 41,5° und β 2 = 180° − 41,5° = 138,5°
β2 scheidet aus, weil im Dreieck der größeren Seite der größere Winkel gegenüberliegen muss. Die Überprüfung mit der
Innenwinkelsumme liefert dieselbe Entscheidung.
© Rhön-Gymnasium Bad Neustadt
09
Seite 3 von 14
10
Grundwissen Mathematik
4
Trigonometrische Funktionen
y
1
O
1
2
3
4
5
6 x
-1
Sinusfunktion f(x) =sin x mit Df = IR .
punktsymmetrisch zu (0/0); Periodenlänge 2π; Wf = [-1;1]
Kosinusfunktion f(x) = cos x mit Df = IR .
achsensymmetrisch zur y-Achse; Periodenlänge 2π; Wf = [-1;1]
y
2
Tangensfunktion f(x) = tan x
mit Df = IR \ {(2z + 1) π2 }
1
O
1
2
3 x
-1
punktsymmetrisch zu (0/0);
Periodenlänge π; Wf = IR
-2
© Rhön-Gymnasium Bad Neustadt
09
Seite 4 von 14
10
Grundwissen Mathematik
Die allgemeine Sinusfunktion
f (x) = a sin[b(x + c)] + d mit a, b ≠ 0 Periode
2π
b
a: Streckung oder Stauchung in y-Richtung
b: Streckung oder Stauchung in x-Richtung
c: Verschiebung nach rechts ( c < 0) oder links (c > 0)
d: Verschiebung nach oben (d > 0) oder unten (d < 0)
5
Exponentialfunktion
5.1 Exponentielles Wachstum
Ist die Änderung pro Zeiteinheit direkt proportional zum aktuellen Bestand, so liegt ein exponentielles Wachstum oder
eine exponentielle Abnahme vor. (x im Exponenten)
x
Wachstumsgesetz y = b ⋅ a
b: Anfangswert
a: Wachstumsfaktor oder Abnahmefaktor
a>1 exponentielle Zunahme,
0<a<1 exponentielle Abnahme
© Rhön-Gymnasium Bad Neustadt
09
Seite 5 von 14
10
Grundwissen Mathematik
5.2 Exponentialfunktionen
y = a x a ∈ IR + , x ∈ IR
( 12 )
x
( )
1
10
+
W = IR
streng monoton steigend
für a>1
streng monoton fallend
für 0<a<1
Die Graphen von
y = a x und y = ( 1a )
y
4
10x
2x
3
2
x
1
sind zueinander
symmetrisch bzgl. der yAchse.
6
x
-2
-1
O
1
2 x
Logarithmus
Ist b ∈ IR + \ {1} und b x = a , so heißt der Exponent x der Logarithmus von a zur Basis b: x = log b a .
( log b a ist diejenige Zahl, mit der man b potenzieren muss,
um a zu erhalten.)
log b 1 = 0; l og b b = 1
log b b x = x; blogb x = x
© Rhön-Gymnasium Bad Neustadt
09
Seite 6 von 14
10
Grundwissen Mathematik
6.1 Rechnen mit Logarithmen
log b (u ⋅ v) = log b u + log b v
log b (u : v) = log b u − log b v
log b u z = z ⋅ log b u
(b, u, v ∈ IR + , b ≠ 1, z ∈ IR)
2 ⋅ logb x + 3logb y − log b z = logb
1
1
logb b − 4 logb a = − 4 logb a
a
2
2
log b x
Basisumrechnung: log a x =
log b a
logb
b
x2 y3
z
4
=
Zehnerlogarithmus: Schreibweise: lg x := log10 x
Praxis: Auf dem TR ist die Zehnerlogarithmus-Taste mit log
beschriftet!
Näherungsweises Berechnen von Logarithmen mit beliebiger
log 5
≈ 2,3219
Basis auf dem TR z.B. log 2 5 =
log 2
© Rhön-Gymnasium Bad Neustadt
09
Seite 7 von 14
10
Grundwissen Mathematik
6.2 Exponential- und Logarithmusgleichungen
Variable im Exponenten – Lösungsprinzip –
2 x = 32 x −1 | logarithmieren
lg 2 x = lg 32 x −1
x lg 2 = ( 2x − 1 )lg 3 nach x auflösen
x lg 2 = 2x lg 3 - lg 3
x lg 2 − 2x lg 3 = − lg 3
x(lg 2 − 2 lg 3 ) = − lg 3
x=
− lg 3
lg 2 − 2 lg 3
Variable im Logarithmus – Lösungsprinzip –
log 5 ( 2x + 1 ) = 3 |delogarithmieren
5 3 = 2x + 1
x = 62
7
Ganzrationale Funktionen
Ein Term der Form
a n x n + a n −1 x n −1 + ... + a 2 x 2 + a1 x + a 0 mit a 0 ...a n ∈ IR; a n ≠ 0
heißt Polynom n-ten Grades.
© Rhön-Gymnasium Bad Neustadt
09
Seite 8 von 14
10
Grundwissen Mathematik
Eine Funktion der Form
f : x 6 a n x n + a n −1 x n −1 + ...x 2 + a1 x + a 0 mit a 0 ...a n ∈ \;a n ≠ 0
mit Df = \ heißt ganzrationale Funktion n-ten Grades.
7.1 Potenzfunktionen
Jede Funktion f(x) = xn mit Df = IR und n ∈ IN heißt Potenzfunktion mit natürlichem Exponenten.
y
5
x4
y
x2
x5 x3
2
4
1
3
-2
2
-1
1
2 x
-1
1
-2
-2
-1 O
1
2 x
n gerade
Wf = IR 0+
achsensymmetrisch zur y Achse
gemeinsam (–1|1), (0|0), (1|1)
© Rhön-Gymnasium Bad Neustadt
-3
n ungerade
Wf = IR
punktsymmetrisch zu (0|0)
gemeinsam (–1|–1), (0|0), (1|1)
09
Seite 9 von 14
10
Grundwissen Mathematik
7.2 Polynomdivision
(6x ): (3x ) =
3
6x 3 + 16x 2 − 7x − 10 : (3x + 2 ) = 2x 2 + 4x − 5
−(6x 3 + 4x 2 )
(3x + 2) ⋅ 2x 2
12x 2 − 7x
12x2 : (3x) =
− (12x 2 + 8x )
− 15x − 10
−(−15x − 10)
usw.
0
7.3 Nullstellen
f ist eine ganzrationale Funktion n-ten Grades.
Dann hat sie höchstens n Nullstellen.
Ist x = a Nullstelle von f, so gilt f(x) = (x–a)·g(x) mit Grad
g(x) = n–1.
7.4 Grenzwert
Unterscheiden sich die Funktionswerte von f(x) für x → ∞ bzw.
x→ –∞ beliebig wenig von der Zahl a, so konvergiert f(x) gegen
den Grenzwert a.
lim f (x) = a bzw. lim f (x) = a
x →∞
x →−∞
© Rhön-Gymnasium Bad Neustadt
09
Seite 10 von 14
10
Grundwissen Mathematik
7.5 Felder abstreichen
f(x) = x3 – x = x(x+1)(x–1)
NST x1 = –1, x2 = 0, x3 = 1
–1 0 1
x
– – + +
x+1 – + + +
x-1 – – – +
f(x) – + – +
y
3
2
f(x)
1
-2
7.6 Symmetrie
f(-x)
f(-x) = –f(x)
Graph punktsymmetrisch
zu (0|0).
-1
O
1
x
-1
-2
-3
y
2
f(-x)
-2
f(x)
1
-1
O
1
f(-x) = f(x)
Graph achsensymmetrisch
zur y-Achse
x
© Rhön-Gymnasium Bad Neustadt
09
Seite 11 von 14
10
Grundwissen Mathematik
8
Zusammengesetzte Zufallsexperimente
8.1 Bedingte Wahrscheinlichkeit
heißt für P(B) ≠ 0 die bedingte Wahrscheinlichkeit von A unter der Bedingung
B.
oder Wahrscheinlichkeit von A unter der Bedingung, dass B eingetreten ist, oder Wahrscheinlichkeit von A im Ergebnisraum B.
PB (A) =
P(A ∩ B)
P(B)
Bsp.: Bei einer Befragung von 80 Personen geben 65 an Englisch
und 55 Französisch zu sprechen. Von denen die Englisch sprechen, sprechen 45 auch Französisch.
PE (F) =
P(E) =
65
80
45
65
P(E ∩ F)
⊕ = P(F) =
E
F
P(E ∩ F)
PE (F)
F
P(E ∩ F)
PE (F)
F
P(E ∩ F)
PE (F) =
15
P(E) =
80
F
20
65
55
80
E
© Rhön-Gymnasium Bad Neustadt
09
Seite 12 von 14
10
Grundwissen Mathematik
55 65 45 10
− ⋅
=
80 80 65 80
Mit welcher Wahrscheinlichkeit spricht unter denen, die kein
Englisch sprechen, jemand Französisch?
10
P(E ∩ F) 80 10
=
=
;
PE (F) =
15 15
P(E)
80
Mit welcher Wahrscheinlichkeit spricht unter denen, die kein
Englisch sprechen, jemand auch kein Französisch?
10 5
PE (F) = 1 − =
15 15
5
P(„keine der beiden Sprachen“) = P(E ∩ F) = P(E) ⋅ PE (F) =
80
Mit welcher Wahrscheinlichkeit spricht unter denen, die Französisch sprechen, jemand auch Englisch?
65 45
⋅
P(E ∩ F) 80 65 45
=
=
PF (E) =
55
P(F)
55
80
a) P(„nur F“) = P(E ∩ F) = P(F) − P(E ∩ F) =
b)
c)
d)
e)
Lösung der Aufgaben mit der Vierfeldertafel
(Nur anwendbar bei zwei Ereignissen)
© Rhön-Gymnasium Bad Neustadt
09
Seite 13 von 14
10
Grundwissen Mathematik
8.2 Vierfeldertafel
Vierfeldertafel mit der absoluten Häufigkeit.
+
E E Gesamt
F
45 10
55
20 5
25
F
Gesamt 65 15
80
a) 10 sprechen nur Französisch. P(„nur F“) =
10
80
10
15
5
c) PE (F) =
15
b) PE (F) =
d) P(E ∩ F) =
5
80
45
55
Vierfeldertafel mit der Wahrscheinlichkeit.
+
E E Gesamt
45
10
55
F
80
80
80
e) PF (E) =
F
20
80
5
80
25
80
Gesamt
65
80
15
80
1
© Rhön-Gymnasium Bad Neustadt
09
Seite 14 von 14