WS2008/09 Blatt 12
Werbung

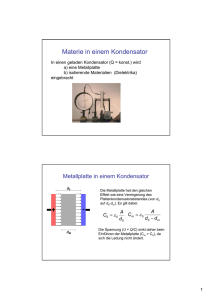
Lehrstuhl für Technische Elektrophysik TU München Tutorübungen zu “Elektromagnetische Feldtheorie 1”, Prof. Wachutka, WS0809, Blatt 12 1. Aufgabe Ein zylinderförmiges Dielektrikum mit der ortsabhängigen, isotropen relativen Permittivität εr (r), der Länge L und dem Radius 2R1 ist metallisch ummantelt und von Vakuum umgeben. Im Dielektrikum befindet sich die zylindersymmetrische Ladungsdichte ⎧ ⎪ ⎨ ρ(r) = ⎪ ⎩ ρ0 ρ0 R1 , 0 ≤ r < R1 , 1 , R1 ≤ r < 2R1 r wobei ρ0 eine konstante Ladungsdichte ist. Die Länge L des Dielektrikums ist groß verglichen mit dessen Radius 2R1 , so daß die Streufelder an den beiden Stirnflächen des Dielektrikums vernachlässigbar sind. a) Bestimmen Sie im Dielektrikum aus der gegebenen Ladungsdichte ρ(r) die dielektri r ). Welche Oberflächenladungsdichte σr=2R (r) muß sich auf sche Verschiebung D( 1 r) dem metallischen Außenmantel befinden, damit die dielektrische Verschiebung D( außerhalb des Dielektrikums verschwindet? b) Wie muß die relative Permittivität εr (r) gewählt werden, damit sie auf der z-Achse r)| überall im Dielekden Wert 1 annimmt und der Betrag des elektrischen Felds |E( trikum linear mit dem Radius r ansteigt? Ist die ermittelte relative Permittivität εr (r) im gesamten Dielektrikum stetig? r ), wenn c) Mit welcher Ladungsdichte ρtot (r) erhält man das gleiche elektrische Feld E( kein Dielektrikum vorhanden ist? d) Bestimmen Sie die Polarisation P (r) und die Polarisierungs-Volumenladungsdichte ρpol (r) im Dielektrikum. Wie groß ist die Polarisierungs-Oberflächenladungsdichte σpol,r=2R1 (r) am Außenmantel? r ) des Dielektrikums gepeicherte Energiee) Berechnen Sie die im elektrischen Feld E( dichte wel (r) und die gespeicherte Gesamtenergie Wel . f) Wird ein Volumenelement des Dielektrikums in beliebiger Richtung um ein kleines Stück δr verschoben, kann sich dessen elektrische Energiedichte wel (r) ändern. Wie r ) von der elektrischen Energiedichte wel (r) ab, wenn diese hängt die Kraftdichte f( als potentielle Energiedichte ψ(r) interpretiert werden kann? Welche Kraftdichte f(r) wirkt auf das Dielektrikum? Lehrstuhl für Technische Elektrophysik TU München Tutorübungen zu “Elektromagnetische Feldtheorie 1”, Prof. Wachutka, WS0809, Blatt 12 2. Aufgabe Zwei Metallplatten der Fläche A, die sich im Abstand 2d voneinander befinden, bilden einen Plattenkondensator. In diesem liegen zwei Dielektrika mit unterschiedlichen elektrischen Suszeptibilitäten, so daß im Plattenkondensator für die elektrische Suszeptibilität χ= ⎧ ⎨ 1 ,0<x<d ⎩ 2 , d ≤ x < 2d gilt. Außerhalb des Plattenkondensator befindet sich Vakuum. Auf der unteren Metallplatte bei x = 0 und der oberen Metallplatte bei x = 2d befinden sich die Ladungen −Q und Q. Der Abstand 2d der beiden Metallplatten ist klein verglichen mit der Fläche A, so daß die Streufelder am Rand vernachlässigt werden können. r) zwischen den beiden Metallplata) Bestimmen Sie die dielektrische Verschiebung D( ten. b) Leiten Sie den allgemeinen Zusammenhang zwischen der Polarisation P (r) und der r ) her. Bestimmen Sie damit die Polarisation P (r) dielektrischen Verschiebung D( im Plattenkondensator. Wie groß ist die Polalarisierungs-Grenzflächenladungsdichte σpol,x=d (r) zwischen den beiden Dielektrika? Im Folgenden darf die Ladung auf der oberen Metallplatte vom Wert Q abweichen. c) Welche Grenzflächenladungsdichte σx=d (r) muß sich zwischen den Dielektrika befin r ) zu erhalten? den um im Plattenkondensator ein konstantes elektrisches Feld E( Wie groß ist die Polarisation P (r) im Plattenkondensator und die PolalarisierungsGrenzflächenladungsdichte σpol,x=d(r) zwischen den Dielektrika nun? d) Wie muß die Grenzflächenladungsdichte σx=d (r) gewählt werden damit die Polalarisierungs-Grenzflächenladungsdichte σpol,x=d (r) zwischen den Dielektrika verschwindet? Pol1. Lösungsskizze r ) wird mit Hilfe der Maxwellgleichung a) Die dielektrische Verschiebung D( ∂V r ) · da = D( V ρ(r)d3 r aus der vorgegebenen Ladungsverteilung ρ(r) bestimmt. Da es sich um ein zylindersymmetrisches Problem handelt, werden für die Berechung Zylinderkoordinaten verwendet. In diesen ergibt sich das Flächenelement zu da = er rdzdϕ, das Volumen r) = Dr (r)er . element zu d3 r = ξdzdϕdξ und die dielektrische Verschiebung zu D( r) in den Richtungen eϕ und Die Komponenten der dielektrischen Verschiebung D( ez sind aus Symmetriegründen gleich Null. Als Hüllfläche ∂V wird ein Zylinder mit dem Radius r und der Länge L gewählt. 2π L ϕ=0 z=0 Dr (r)er · er rdzdϕ = r 2π L ξ=0 ϕ=0 r 2πlrDr (r) = 2πl Dr (r) = für 0 ≤ r < R1 : ρ(ξ)ξdzdϕdξ ρ(ξ)ξdξ 1 r ρ(ξ)ξdξ r ξ=0 1 r 1 ρ0 2 ρ0 Dr (r) = ρ0 ξdξ = r = r r ξ=0 r 2 2 ρ 0 r ) = rer D( 2 für R1 ≤ r < 2R1 : für r ≥ 2R1 : ξ=0 z=0 1 1 R1 1 r Dr (r) = ρ0 ξdξ + ρ0 ξdξ r ξ=0 r ξ=R1 ξ 2 ρ0 R12 1 1 ρ0 R1 1 + ρ0 R1 (r − R1 ) = − + ρ0 R1 = r 2 r 2 r 2 1 R ρ 0 1 r) = − + ρ0 R1 er D( 2 r Dr (r) = 1 r R1 ξ=0 ρ0 ξdξ + 1 r 2R1 1 ρ0 ξdξ ξ ξ=R1 1 r σr=2R1 (r)δ (ξ − 2R1 ) ξdξ r ξ=2R1 1 1 ρ0 R12 1 + ρ0 R1 (2R1 − R1 ) + σr=2R1 (r)2R1 = 0 = r 2 r r 2 3ρ0 R1 1 1 = + 2R1 σr=2R1 (r) = 0 2 r r 3ρ0 R1 σr=2R1 (r) = − 4 + r) b) In einem isotropen Dielektrikum gilt zwischen der dielektrische Verschiebung D( r ) der Zusammenhang und dem elektrischen Feld E( r ). r ) = εr (r)ε0 E( D( Aufgrund der Zylindersymmetie und des geforderten linearen Anstiegs des elektri r )| mit dem Radius r gelten D( r ) = Dr (r)er und E( r) = schen Feldbetrags |E( (E0 r/R1 )er , wobei E0 eine konstante elektrische Feldstärke ist. E0 r er R1 R1 Dr (r) 1 εr (r) = ε0 E0 r Dr (r)er = εr (r)ε0 ρ0 R1 2ε0 E0 Insbesondere soll die relative Permittivität εr (r) auf der z-Achse, also für r = 0, den Wert 1 annehmen. Mit dieser Bedingung kann die noch unbekannte Konstante E0 bestimmt werden. für 0 ≤ r < R1 : εr (r) = ρ0 R1 =1 2ε0 E0 ρ0 R1 E0 = 2ε0 εr (r) = 1 εr (r = 0) = für R1 ≤ r < 2R1 : εr (r) = − ρ0 R13 1 ρ0 R12 1 1 2 1 + + 2R = −R 1 1 2ε0 E0 r 2 ε0 E0 r r2 r In den beiden Bereichen 0 ≤ r < R1 und R1 ≤ r < 2R1 wird die relative Permittivität εr (r) jeweils durch stetige Funktionen εr,0≤r<R1 (r) und εr,R1 ≤r<2R1 (r) dargestellt. Besitzen die beiden Funktionen für r = R1 den gleichen Wert, so ist die Permittivität im gesamten Dielektrikum stetig. εr,0≤r<R1 (r = R1 ) = εr,R1 ≤r<2R1 (r = R1 ) 1 = −R12 1 1 + 2R1 2 R1 R1 1 = 1 Die Permittivität εr (r) ist also im gesamten Dielektrikum stetig. c) Für die Berechnung der Ladungsdichte ρtot (r) wird ebensfalls die Maxwellgleichung ∂V r) · da = D( V ρtot (r)d3 r verwendet. Diesemal jedoch in der differentiellen Form r ) = ρtot (r). divD( r) = Aufgrund des fehlenden Dielektrikums und dem elektrischen Feld E( r) = ε0 E( r) = (ρ0 /2ε0)rer erhält man für die dielektrische Verschiebung D( (ρ0 /2)rer . Die Divergenz in Zylinderkoordinaten vereinfacht sich aufgrund der fehlenden Abhängikeiten von ϕ und z zu div = 1/r(∂/∂r)r. 1 ∂ ρ0 r r = ρtot (r) r ∂r 2 ρtot (r) = ρ0 d) Die im Dielektrikum ebenfalls zylindersymmetrische Polarisation P (r) = Pr (r)er wird mit der Gleichung r ) − ε0 E( r) P (r) = D( Pr (r)er = Dr (r)er − ε0 Er (r)er Pr (r) = Dr (r) − ε0 Er (r) bestimmt, wobei die Beziehung Er (r) = (ρ0 /2ε0)r verwendet wird. für 0 ≤ r < R1 : ρ0 ρ0 r − ε0 r=0 2 2ε0 P (r) = 0 Pr (r) = ρ0 ρ0 R12 1 + ρ0 R1 − ε0 r 2 r 2ε0 ρ0 R12 1 ρ0 − r + ρ0 R1 =− 2 r 2 2 ρ0 R1 1 ρ0 P (r) = − − r + ρ0 R1 er 2 r 2 für R1 ≤ r < 2R1 : P (r) = − Die Polarisierungs-Volumenladungsdichte ρpol (r) im Dielektrikum erhält man aus der ermittelten Polarisation P (r) mit der Gleichung ρpol (r) = −divP (r) = − 1 ∂ rPr (r). r ∂r für 0 ≤ r < R1 : ρpol (r) = − 1 ∂ r·0 =0 r ∂r für R1 ≤ r < 2R1 : 1 ∂ ρ0 R12 1 ρ0 r − − r + ρ0 R1 ρpol (r) = − r ∂r 2 r 2 1 1 = − (−ρ0 r + ρ0 R1 ) = ρ0 − ρ0 R1 r r Die Polarisierungs-Oberflächenladungsdichte σpol,r=2R1 (r) am Außenmantel, dessen vom Dielektrikum wegzeigende Flächennormale n = er lautet, wird ebenfalls aus der der Polarisation P (r) = Pr (r)er berechnet. σpol,r=2R1 (r) = P (r = 2R1 ) · n = Pr (r = 2R1 )er · er = − ρ0 R12 1 ρ0 ρ0 R1 − 2R1 + ρ0 R1 = − 2 2R1 2 4 e) Die elektrische Energiedichte wel (r) ergibt sich aus dem halben Produkt der dielektri r) = (ρ0 /2ε0 )rer . r ) = Dr (r)er mit dem elektrischen Feld E( schen Verschiebung D( 1 r) D(r) · E( 2 1 ρ0 Dr (r)er · rer wel (r) = 2 2ε0 ρ0 wel (r) = rDr (r) 4ε0 wel (r) = für 0 ≤ r < R1 : wel (r) = ρ2 ρ0 ρ0 r = 0 r2 4ε0 2 8ε0 ρ0 ρ0 R12 1 ρ2 R2 ρ2 R1 + ρ0 R1 = − 0 1 + 0 r wel (r) = − 4ε0 2 r 8ε0 4ε0 für R1 ≤ r < 2R1 : r ) insgesamt gespeicherte elektrische Energie Wel erhält Die im elektrischen Feld E( man durch räumliche Integration der elektrische Energiedichte wel (r). Wel = R1 2π L r=0 = 2πL ϕ=0 R1 r=0 = 2πL R1 r=0 = 2πL ρ20 32ε0 z=0 wel (r)rdzdϕdr + wel (r)rdr + 2πL ρ20 2 r rdr + 2πL 8ε0 R14 + 2πL − 3 7 πρ20 LR14 1 − + ε0 16 8 6 41πρ20 LR14 = 48ε0 2R1 r=R1 2R1 2π L r=R1 r=R1 16ε0 z=0 wel (r)rdzdϕdr wel (r)rdr 2R1 ρ20 R12 ϕ=0 ρ20 R12 ρ20 R1 − + r rdr 8ε0 4ε0 2 (2R1 ) − R12 ρ20 R1 + (2R1 )3 − R13 12ε0 = f) Eine Potentialänderung bei Verschiebung eines Körpers entspricht einer Arbeit, welche für kleine Verschiebungen gleich dem skalaren Produkt aus Kraft und Weg ist. Das Gleiche gilt für die entsprechenden Dichten. δψ(r) = ∂ψ(r) · δr = f(r) · δr ∂r Da die elektrische Energiedichte wel (r) als potentielle Energiedichte ψ(r) interpretiert werden kann und der Gradienten in Zylinderkoordinaten ∂/(∂r) = ∂/(∂r)er bei Unabhängigkeit von ϕ und z lautet, erhält man für die Kraftdichte ∂wel (r) ∂wel (r) ∂ψ(r) = = er . f(r) = ∂r ∂r ∂r für 0 ≤ r < R1 : ∂wel (r) ∂ er = f(r) = ∂r ∂r ρ20 2 ρ2 r er = 0 rer 8ε0 4ε0 ∂wel (r) ∂ ρ2 R2 ρ2 R1 er = f(r) = − 0 1 + 0 r er ∂r ∂r 8ε0 4ε0 für R1 ≤ r < 2R1 : = ρ20 R1 er 4ε0 2. Aufgabe r ) zwischen den beiden Metallplatten wird mit a) Die dielektrische Verschiebung D( Hilfe der Maxwellgleichung ∂V r ) · da = D( V ρ(r)d3 r ermittelt. Dazu wird um die untere Metallplatte eine quaderförmige Hüllfläche gelegt. Aufgrund der gleich stark positiv geladenenen oberen Metallplatte befinden sich sämtliche negativen Ladungen der unteren Metallplatte an der Grenzfläche zum Dielektrikum. Damit trägt nur der zwischen den Metallplatten befindliche Teil der Hüllfläche, der den Normalenvektor ex und die Fläche A besitzt, zum Oberflächenintegral bei, da die Streufelder vernachlässigt werden sollen. Das Volumenintegral über die Ladungsdichte ρ(r) ist gleich der eingeschlossenen Ladung −Q. ∂V r) · da = D( V ρ(r)d3 r r ) · Aex = −Q D( r ) = − Q ex D( A b) Um den allgemeinen Zusammenhang zwischen der Polarisation P (r) und der dielek r ) herzuleiten, werden die Beziehungen D( r ) = P (r) + trischen Verschiebung D( r ), D( r) = εr (r)ε0 E( r ) und εr (r) = χ(r) + 1 verwendet. ε0 E( r) r) − ε0 E( P (r) = D( r) − ε0 D(r) = D( εr (r)ε0 εr (r) − 1 D(r) = εr (r) = χ(r) D(r) χ(r) + 1 Mit χ(r) = 1 für 0 < x < d und χ(r) = 2 für d ≤ x < 2d ergibt sich daraus die Polarisation P (r) im Plattenkondensator. für 0 < x < d: für d ≤ x < 2d: χ(r) Q Q 1 − ex = − ex D(r) = χ(r) + 1 1+1 A 2A 2 χ(r) Q 2Q D(r) = P2 (r) = − ex = − ex χ(r) + 1 2+1 A 3A P1 (r) = Die Polarisierungs-Grenzflächenladungsdichte σpol,x=d (r) zwischen den beiden Dielektrika berechnet sich aus σpol,x=d(r) = P1 (r) ·n1 + P2 (r) ·n2 . Dabei sind P1 (r) und P2 (r) die Polarisationen in den beiden Dielektrika bei 0 < x < d und d ≤ x < 2d. Die Vektoren n1 = ex und n2 = −ex sind die vom jeweiligen Dielektrikum wegzeigenden Normalenvektoren der Grenzfläche. σpol,x=d(r) = P1 (r) · n1 + P2 (r) · n2 Q 2Q ex · ex − ex · (−ex ) 2A 3A Q = 6A = − c) Da sich die Ladung −Q auf der unteren Metallplatte nicht ändert, bleibt die di r) im unteren Dielektrikum (0 < x < d) gleich. Mit elektrische Verschiebung D( r) = εr (r)ε0 E( r ) und εr (r) = χ(r) + 1 erhält man damit das elektrische Feld D( r ) im unteren Dielektrikum. E( Q ex − D(r) D(r) Q A E(r) = ex = = =− εr (r)ε0 (χ(r) + 1) ε0 (1 + 1) ε0 2ε0 A r ) auch im oberen Dielektrikum (d ≤ x < 2d) herrSoll dieses elektrische Feld E( r) dort schen, ist die dielektrische Verschiebung D( r ) = (χ(r) + 1) ε0 E( r) = (2 + 1) ε0 − Q ex = − 3Q ex . 2 (r) = εr (r)ε0 E( D 2ε0 A 2A 1 (r) · n1 + D 2 (r) · n2 erhält man die für Damit und der Beziehung σx=d (r) = D r ) erforderliche Grenzflächenladungsdichte σx=d (r). das konstante elektrische Feld E( Für diese Formel zeigen die Normalenvektoren der Grenzfläche n1 = −ex und n2 = 1 (r) = D( r) ex ins jeweilige Dielektrikum mit den dielektrischen Verschiebungen D 2 (r). und D 1 (r) · n1 + D 2 (r) · n2 σx=d (r) = D Q 3Q = − ex · (−ex ) − ex · ex A 2A Q = − 2A r ) im unAus demselben Grund aus dem sich die dielektrische Verschiebung D( teren Dielektrikum nicht geändert hat, ändert sich dort auch die Polarisierung P (r) nicht. Im oberen Dielektrium kann die Polarisierung P (r) mit der Beziehung r) bestimmt werden. P (r) = χ(r)ε0 E( für 0 < x < d: Q P1 (r) = − ex 2A für d ≤ x < 2d: r) = 2ε0 − Q ex = − Q ex P2 (r) = χ(r)ε0 E( 2ε0 A A Aus der ermittelten Polarisierung P (r) kann nun wie in Teilaufgabe b) die Polarisierungs-Grenzflächenladungsdichte σpol,x=d (r) bestimmt werden. σpol,x=d(r) = P1 (r) · n1 + P2 (r) · n2 Q Q ex · ex − ex · (−ex ) 2A A Q = 2A = − d) Damit die Polarisierungs-Grenzflächenladungsdichte σpol,x=d (r) and der Grenzfläche der beiden Dielektrika verschwindet muß die Polarisierung P (r) dort stetig sein. σpol,x=d(r) = P1 (r) · n1 + P2 (r) · n2 0 = P1 (r) · ex + P1 (r) · (−ex ) P1 (r) = P2 (r) Damit ist die Polarisierung P (r) im gesamten Plattenkondensator konstant und die r ) im oberen Dielektrikum kann mit der Beziehung dielektrische Verschiebung D( r)/ (χ(r) + 1) ermittelt werden. Im unteren Dielektrikum hat sich P (r) = χ(r)D( r) nicht verändert. die dielektrische Verschiebung D( für 0 < x < d: für d ≤ x < 2d: 1 (r) = − Q ex D A 2+1 χ(r) + 1 Q 3Q P (r) = D2 (r) = − ex = − ex χ(r) 2 2A 4A Die gesuchte Grenzflächenladungsdichte σx=d (r) kann damit wie in Teilaufgabe c) berechnet werden. 1 (r) · n1 + D 2 (r) · n2 σx=d (r) = D Q 3Q = − ex · (−ex ) − ex · ex A 4A Q = 4A