Isotrope Dielektrika

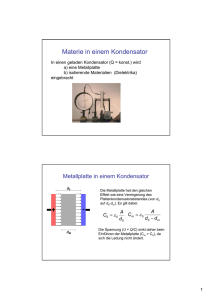
Ergänzungen zu Physik II
Isotrope Dielektrika
Isotrope Dielektrika
2|
Das Coulombsche Gesetz in der Form F =1/(4π0 ) |q1r||q
ist nur für zwei Ladungen im Vakuum gültig.
2
Versuche mit der Cavendish-Drehwaage mit flüssigen oder gasförmigen Isolatoren zwischen den beiden
Ladungen ergeben stets Kräfte, die kleiner sind als jene, die im Vakuum auftreten. Das Medium, der
Isolator zwischen den Ladungen, nach M. Faraday Dielektrikum genannt, hat also einen Einfluss auf die
elektrischen Felder.
In der Natur gibt es keine vollkommenden Nichtleiter bzw. Isolatoren, jedoch ist der Ladungstransport
in einem Isolator so gering, dass wir Isolatoren in sehr guter Näherung als ideale Nichtleiter behandeln
können. Isolatoren sind für das elektrische Feld durchlässig, während Leiter das Feld abschirmen. Wie
gerade erwähnt bezeichnet man Isolatoren als Dielektrika.
Zum Spannungsbegriff V =
2 s
Dielektrikum
3 s
s1
s4
R
~ r in einem Plattenkondensator mit Dielektrikum:
Ed~
Für einem Plattenkondensator, in dem in der oberen Hälfte ein Dielektrikum steckt, muss nach
R der Definition der Spannung als Arbeit pro
~ r = qV ) die Spannung zwischen den PunkLadungseinheit (W = q Ed~
ten 2-1 und 3-4 gleich und die Arbeit über den Weg 1-2-3-4 null sein.
+
−
D.h.:
(i) Die Wege 2-3 und 4-1 laufen auf Äquipotentialflächen und die Arbeit ist null.
(ii) In Anbetracht der Nichtexistenz eines Perpetuum mobile 1. Art muss gelten: W1−2 = −W3−4 .
Die Spannungsdefinition mit oder ohne ein Dielektrikum bleibt damit gleich. Bezüglich des Einflusses
nichtleitender Materie (Isolatoren, Dielektrika) auf elektrische Felder zeigen Experimente Folgendes:
À Wird ein Dielektrikum zwischen die Platten eines geladenen Kondensators geschoben, wobei sich die
Ladung nicht ändert, so verkleinert sich die ursprüngliche Potentialdifferenz V1 − V2 , respektive wird
~ oder der effektive Plattenabstand reduziert. Das Ausmass der Verkleinerung
die elektrische Feldstärke E
hängt vom jeweiligen Material ab.
+Q
~
E
?
−Q
6
d
?
A
A V1 − V2
=V
Á Wird ein Dielektrikum zwischen die Platten eines geladenen Kondensators geschoben, wobei mit einer angelegten Batterie die Spannung konstant gehalten wird,
dann erhöht sich die Ladung des Kondensators und es
fliesst ein Strom.
Q =konst.
+Q
~0 < E
~
E
?
−Q
+Q0
~
E
?
−Q0
A
0
0
A V1 − V2
0
=V <V
I
Q0 > Q
V =konst.
Der mikroskopische Grund hierfür liegt darin, dass auch Isolatoren aus positiven und negativen Ladungen
bestehen. Wird nun ein Isolator in ein elektrische Feld gebracht, so können in den Atomen elektrische Dipolmomente induziert oder in Molekülen bereits vorhandene Dipolmomente im Feld ausgerichtet werden.
.
j
Das Dipolmoment wird definiert als
p~ = q · d~ ,
(1)
d~
*+
−q +q
wobei seine Richtung definitionsgemäss von der negativen zur positiven Ladung
−j
zeigt. Der Abstand d~ ist ein Mass für die Asymmetrie der Ladungen.
~
E
Im äusseren elektrischen Feld werden also positive und negative Ladungen
66666666
± ± ± ± ± ± ± ± ± +σp
gegeneinander verschoben; die Materie wird polarisiert. Während sich die
± ± ± ± ± ± ± ± ±
Ladungen im Inneren des Körpers immer noch aufheben, treten an den
± ± ± ± ± ± ± ± ±
Oberflächen Ladungen +σp , −σp auf, wobei der Körper als Ganzes neutral
± ± ± ± ± ± ± ± ±
−σp
1
Ergänzungen zu Physik II
~
F~ = −q E
−j
j d~ *+ ~
~
F = qE
Isotrope Dielektrika
bleibt; er besitzt nun ein elektrisches Dipolmoment. Daher können auch
Isolatoren in elektrischen Feldern Kräfte erfahren. Ein konstantes Feld
~ und dreht die einzelnen Dipole,
erzeugt ein Drehmoment ~τ = q · d~ × E
während ein inhomogenes, mit dem Ort sich änderndes Feld eine Kraft
~ auf die Dipole ausübt.
F~ = ∇(q d~E)
Die Polarisation P~ eines Körpers ist definiert als Dipolmomente pro Volumeneinheit p~/∆V . Sie hat für
~ und es gilt
isotrope Dielektrika die Richtung des angelegten Feldes E,
C
As V
.
~
~
.
(2)
P = χe ε◦ E
·
=
Vm m
m2
χe ist die materialabhängige elektrische Suszeptibilität. Sie kann mittels einer Federkonstanten k zwischen
~
~
den zwei Ladungen interpretiert werden: Seien kd = F = eE, p~ = ed~ = e2 E/k,
dann ist P~ = e2 E/(k
∆V )
und χe = e2 /(kε◦ ∆V ). Da die elektrische Suszeptibilität dimensionslos ist, hat P~ die Dimension von
~ [C/m2 ]. Wir betrachten nun ein rechteckiges Stück Dielektrikum der Dicke d und der Fläche A
ε◦ E
~ Das gesamte Dipolmoment ist Polarisation·Volumen“, also P · ∆V = P · Ad.
im elektrischen Feld E.
”
Anderseits ist ein Dipolmoment definiert als Ladung · Abstand der Ladungen“, q · d, wonach hier P · A
”
gleich der unbeweglichen Polarisationsladung σp A sein muss:
P · Ad = Qp · d = σp · A · d ,
−Qp = −σp A
PP
q
P
Qp =
-σp A
~ P~
E
σp
d.h. |P~ | = σp .
Hierbei ist σ die bewegliche und σp die feste Polarisationsflächenladungsdichte. Allgemein gilt Pn = σp – die Normalkomponente der
Polarisation ist gleich der Flächenladungsdichte an der Oberfläche eines
Dielektrikums. P~ zeigt mit Gleichung (1) von −σp nach +σp .
d
Dies erklärt die Verkleinerung der Potentialdifferenz im Kondensator. Zusätzlich zu den Ladungen auf
der Kondensatorplatte treten entgegengesetzte Polarisationsladungen σp auf, sodass die Feldstärke im
Innern des Dielektrikums verkleinert wird. Für das effektive Feld E 0 eines ebenen Plattenkondensators
gilt: ε◦ E 0 = σ − σp .
+Q = +σA
Leiter
++++++++++++++++
−−−−−−−−−−−−−−−−
−Qp =−σp A
~ P~ E
~ D
~p
?
E
Dielektrikum
? 6
?
+Qp =+σp A
++++++++++++++++
−−−−−−−−−−−−−−−−
Leiter
−Q = −σA
~ Vac
E
?
Die Anwesenheit polarisierbarer Materie modifiziert ganz allgemein das elektrische Feld. Statt mit der Polarisation und Polarisationsladungen zu rechnen, ist es oft zweckmässig, ein weiteres
Vektorfeld einzuführen, nämlich die dielektrische Verschiebung
.
~ =
~ + P~ .
D
ε◦ E
(3)
Die Bezeichnung Verschiebung wurde von Maxwell eingeführt, um damit die Verschiebung der positiven und negativen Ladungen im Dielektrikum durch das äussere Feld zu charakterisieren. Für den Fall
isotroper1 Dielektrika (Gläser, Plastik, polykristalline Materialien, kubische Kristalle) gilt mit (2), (3):
C
~
~
~
~
~
~
~
P = χe ε◦ E , und mit ε := 1 + χe :
D = ε◦ E + P = ε◦ (1 + χe )E = ε◦ εE
.
(4)
m2
Die dimensionslose Materialkonstante ε heisst relative Dielektrizitätskonstante. Sie spielt eine wichtige
Rolle in der Optik (Bsp. Brechungsindex). χe ist wieder die Suszeptibilität; im Vakuum ist χe = 0, ε = 1
~ = ε◦ E.
~
und damit D
1 Anisotrope
Dielektika sind i.A. nichtkubische Kristalle mit einer Kristallstruktur, die in verschiedenen Raumrichtungen
~ steht nicht parallel zu E.
~
unterschiedlich ist. Die Dielektrizitätskonstante ε ist dann ein Tensor und D
2
Ergänzungen zu Physik II
Isotrope Dielektrika
Dielektrizitätskonstanten ε und χe einiger Materialien
bei Normaldruck und 20◦ C; es ist immer ε > 1.
Material
ε
χe
Material
ε
χe
Vakuum
1
0
Luft
1.00059
0.0059
He
1.000060 0.000060 O2
1.000486 0.000486
Benzol
2.3
1.3
Aceton
21
20
Bernstein
2.8
1.8
TiO2
40. . . 80
40. . . 80
Paraffin
1.9 . . . 2.2
1.1
Glas
5 ...7
4 ...6
Wasser
81
80
Eis
3
2
Zusammenfassung der Grundversuche:
V=konstant
Q=konstant
V = VVac
Q = εQVac > QVac
E = EVac
D = σ = εε◦ E = εε◦ EVac
C = Q/V = εCVac = εε◦ A/d
V = VVac /ε < VVac
Q = QVac
E = EVac /ε < EVac
D = σ = εε◦ E = ε◦ EVac
C = Q/V = εCVac = εε◦ A/d
Mit einem Dielektrikum kann die Kapazität eines Kondensators um ε erhöht werden. (EVac , VVac und
CVac sind die Grössen im Vakuum.)
Der verallgemeinerte Gauss’sche Satz
Für einen Kondensator mit Dielektrikum gilt mit dem Gauss’schen Satz2 ,
EnL = 0
Leiter
6
σ
++++++++++++++++
I
−−−−−−−−−−−−−−−−
σp
E
?n
Dielektrikum
++++++++++++++++
~ A
~=
Ed
Z
En dA =
1
ε◦
H
~ A
~ = qein /0 ,
Ed
Z
(σ − σp )dA =
1
ε◦
Z
(σ − Pn )dA ,
oder mit Q, der wahren Ladung ohne Polarisationsladung,
Z
Z
Z
ε◦ En dA + Pn dA = σdA = Q ;
−−−−−−−−−−−−−−−−
Leiter
~ = ε◦ E
~ + P~ ist, also Dn = ε◦ En + Pn , erhalten wir hieraus den
und da aus Gleichung (3) D
I
allgemeinen Gauss’schen Satz
~ A
~=
Dd
Z
Dn dA = Q
bzw. - in differentieller Form - die 1. Maxwell Gleichung mit Dielektrikum
~ =ρ .
∇·D
(5)
(6)
~
Der Fluss des D-Feldes
durch eine geschlossene Fläche ist gleich der Summe der eingeschlossenen Ladun~
gen. Die Polarisationsladungen sind im D-Feld
enthalten und dürfen auf der rechten Seite der Gleichung
nicht mitgezählt werden. Die differentielle Form Gl.(6) ist die 1. Maxwell Gleichung mit einem Dielektri~ = ρ/ε◦ ) hergeleitet.
kum; sie wird analog zur 1. Maxwell Gleichung3 ohne Dielektrikum (∇E
~ σ, P~ , σp gelöst werden,
Elektrostatische Probleme mit Dielektrika können entweder mit den Grössen E,
~
~
~
oder mit E, σ, D. Da die dielektrische Verschiebung D die Polarisationsladungen bereits einschliesst,
~ das einfachere Feld
müssen nur noch die wahren Ladungen berücksichtigt werden. (Im Allgemeinen ist D
2 Vgl.
Halliday, Kap.24-4.
Ergänzungen Die Poissongleichung“.
”
3 Siehe
3
Ergänzungen zu Physik II
Isotrope Dielektrika
~ abgeleitet werden kann.) Die Feldstärke in einem
zur Berechnung, aus dem dann das physikalische Feld E
Dielektrikum variiert im atomaren Bereich von Ort zu Ort, sie kann daher nur als ein Mittelwert über
einen grösseren Volumenbereich aufgefasst und nicht etwa atomistisch interpretiert werden.
Beispiele zu Dielektrika
Das Verhalten der Feldstärken an den Grenzflächen.
a) Leiter-Dielektrikum Eine geschlossene Gauss’sche Fläche habe die Form einer Pillenschachtel,
~ parallel zur Grenzfläche. E
~ und D
~ stehen senkrecht auf der Leitermit der Grund- und Deckfläche dA
H
~ dA
~=
oberfläche, im Innern des Leiters sind beide Felder null. Mit dem allgemeinen Gauss’schen Satz, D
Q, integriert über die geschlossene Fläche, wobei die Integrale über die Seitenflächen sich aufheben, gilt
Dielektrikum
D · dA = σ · dA also D = D⊥ = σ.
ε
−
~
~
E
+@ − D
Daraus folgt mit D = εε◦ E und D = ε◦ E + P sowie der Eigenschaft, dass
+@ −@
~
P
P~ von −σp nach +σp zeigt (|P~ | = −σp , siehe Gleichung (1)):
+@ −
@
@ @
+ −
@
D
σ
1
@
dA
@ @
E=
=
⇒ σp = −P = ε◦ E − D = −σ 1 −
,
@
@+ @−
εε◦
εε◦
ε
+
@
Leiter
E = 0 @ @−
+@ σp eine Beziehung zwischen σp auf dem Dielektrikum und σ auf dem Leiter.
σ@
D=0
b) Dielektrikum-Dielektrikum
D1n @
R
@
@@
1
@ @@
~
D1
~2 @@
@*
D
@
@
D
@
ε1
2n @
@
@
R
@
@
ε2 @
@
A
E1t
@
@
@
R
@
@
1
D
@ @@
~
@
E1
*
@
~2 E
@
@ @@ B
@ @ ε1
C
@
@
ε@
R
@
2
E2t
Trägt die Trennfläche nur Polarisationsladungen, d.h. σp 6= 0 und σ =
0, so gilt mit Gl. (5) (wobei sich die Flächenintegrale über die Seitenflächen der Pillenschachtel wiederum aufheben): D1n dA − D2n dA = 0, also
~ ist an
D1n = D2n bzw. ε1 E1n = ε2 E2n . Die Normalkomponente von D
~ ändert sprunghaft.
der Trennfläche stetig. Die Normalkomponente von E
Wird ferner ein geschlossener Weg ABCD
betrachtet, wobei AB=CD= d, d
H
~ ~l = 0, integriert über den geschlosparallel zur Trennfläche, so gilt mit Ed
senen Weg, wobei sich die Wegintegrale über die Seitenstrecken senkrecht
zur Trennfläche aufheben (das elektrostatische Feld hat ein Potential, daher
~ = 0): E1t d − E2t d = 0, also E1t = E2t bzw. D1t /ε1 = D2t /ε2 .
gilt ∇ × E
~ ist an der TrennIn Worten ausgedrückt: Die Tangentialkomponente von E
~ hingegen ändert sprunghaft.
fläche stetig, die Tangentialkomponente von D
Die obigen zwei Eigenschaften führt zum Brechungsgesetz der Feldlinien an der Trennfläche (vgl. das
Brechungsgesetz in der Optik): Es ist tan α1 = E1t /E1n und tan α2 = E2t /E2n und damit lautet das
>E
~1
α1 6
ε1
E E1n
1t
6 E2t ε2
E2n
α2
~2
E
Brechungsgesetz
(mit E1t = E2t ) :
tan α1
E2n
ε1
=
=
.
tan α2
E1n
ε2
c) Plattenkondensator mit einem Teil eines Dielektrikums Um die Durchschlagfestigkeit eines
Plattenkondensators bei konstanter Spannung zu verbessern, steckt jemand ein Dielektrikum zwischen
die Platten, das nur einen Teil des Plattenabstandes füllt. Es gilt für den Abstand dε ohne Dielektrikum
4
Ergänzungen zu Physik II
2
V =konst.
ε 6
dε
?
6
ε◦ d
?
Isotrope Dielektrika
V
E0 = d+d
(ohne Dielektrikum), und mit Dielektrikum D1 = ε◦ E1 = D2 = εε◦ E2
ε
⇒ E2 = E1 /ε .
Z2
Somit ist
V =
1
dε
E ds = E1 d + E1 dε = E1 d +
= E0 (d + dε ).
ε
ε
1
Da ε > 1 folgt E0 < E1 , d.h. im Luftspalt wird das Feld grösser und dieser so “ge1
schützte” Kondensator schlägt, wenn mit E1 die Durchschlagsfeldstärke erreicht wird, eher durch. Stattdessen hätte die Dicke des Dielektrikums gerade so gewählt werden müssen, dass d = 0 gegolten hätte.
d) Felder einer Kugel oder einer Punktladung im unendlichen Dielektrikum können wie die
~
E-Felder
im Vakuum geschrieben werden, es muss einzig ε◦ durch εε◦ ersetzt werden:
Q~r
Q~r ~
~
~ r12 ) · Q = Q1 · Q2 ~r12 ;
, E=
. Für zwei Punktladungen Q1 und Q2 gilt F~ = E(~
D=
3
3
3
4πr
εε◦ 4πr
εε◦ 4πr12
durch das Dielektrikum wird die Kraft zwischen den zwei Ladungen gegenüber derjenigen im Vakuum
um den Faktor 1ε verringert.
Eine atomistische Interpretation der Dielektrizitätskonstante
Eine atomistische Interpretation der Dielektrizitätskonstante muss im molekularen Bau der Materie gesucht werden. Es gibt nichtpolare, bezüglich ihrer Ladung symmetrische Moleküle (z.B. CO2 ) und polare,
unsymmetrische (z.B. H2 O):
Nichtpolare Moleküle
x
Die
Schwerpunkte der positiven und negativen Ladungen fallen zuCH4
CO2
Ai
A
sammen,
die symmetrischen Moleküle haben kein permanentes Dipol Cx
A
~
moment.
Ein äusseres E-Feld
verschiebt die Ladungen und induziert
H
H
x
Ax
~ F am Molekül
Oj
Cj
Oj
damit einen elektrischen Dipol proportional zum Feld E
~ F , wobei pm die molekulare elektrische Polarisierbarkeit, eine Konstante des Moleküls, ist. E
~F
p~e = pm · E
ist nicht elementar berechenbar, es hängt vom Einfluss der Nachbarmoleküle ab, kann aber für isotrope
~F = E
~ innen + P~ /(3ε◦ ) .
Substanzen durch das innere Feld und die Polarisation ausgedrückt werden als E
n·p
~ innen + P~ /(3ε◦ )) ⇒ P~ = [(n · pm )/(1 − m )]E
~ innen , und
Für n Moleküle ist dann n · p~e = P~ = n · pm (E
3ε◦
~ = εε◦ E
~ = ε◦ E
~ + P~ sowie P~ = ε◦ (ε − 1)E
~ :
mit D
n · pm
ε−1
– die Clausius-Masotti Formel .
=
3ε◦
ε+2
Damit besteht ein Zusammenhang zwischen der makroskopischen Dielektrizitätskonstanten ε und der
mikroskopischen, molekularen elektrischen Polarisierbarkeit pm . Die induzierten Dipole tragen mit dem
Wert ε zum Wert εε◦ , der absoluten Dielektrizitätskonstanten des Materials, bei. ε ist nicht von der
Temperatur abhängig.
Polare Moleküle
Die Schwerpunkte der positiven und negativen Ladungen fallen nicht
H2 O
HCl
zusammen. Polare, nichtsymmetrische Moleküle haben daher ein perj
O X Hj
j
Hj
Hj
Cl
manentes Dipolmoment p~ = q d~ (mit dem Abstand der beiden Schwer~
punkte d).
As·m
V/m
.10-3 9
P
HCl
1
CH4
1
3
5 .10-3 °C-1
1/T
~
Im E-Feld
erhalten die zunächst ungeordneten Dipole eine Orientierung
in Feldrichtung und erzeugen damit eine Polarisierung des Dielektrikums. Dieser Polarisierung wirkt die Wärmebewegung mit zunehmender
Temperatur entgegen – ε ist von der Temperatur abhängig. Zusätzlich
muss, wie bei den nichtpolaren Molekülen, noch der Anteil der induzierten Dipole berücksichtigt werden.Eine genaue Berechnung der Temperaturabhängigkeit ist elementar nicht möglich. Die Frequenzabhängigkeit
ε = ε(ω) ist wichtig für die Optik.
5