Supraleitung

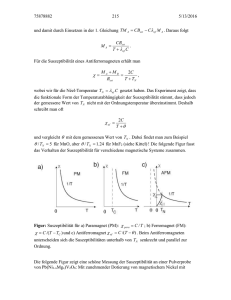
Ingenieurkeramik III
187
8.Kap
Supraleitung
Um die Jahrhundertwende wurden grosse Fortschritte in der
Tieftemperaturforschung gemacht. In diesem Umfeld wurde 1911 das
Phänomen Supraleitung vom niederländischen Experimentalphysiker
Heike Kamerlingh Onnes entdeckt. Onnes, der seine ganze
wissenschaftliche Karriere der Tieftemperaturkühlung widmete,
gelang 1908 als erstem die Verflüssigung von Helium bei 4 Kelvin.
Das flüssige Helium erlaubte ihm die Durchführung von
Experimenten bei Temperaturen, so nahe am absoluten Nullpunkt, wie
sie nie zuvor erreicht wurden.
1911 begann Onnes mit der Untersuchung der elektrischen
Eigenschaften von Metallen bei extrem tiefen Temperaturen. Damals
war wohlbekannt, dass der elektrische Widerstand mit sinkender
Temperatur abnimmt. Heftig diskutiert wurde jedoch, wie sich der
Widerstand in der Nähe des absoluten Nullpunktes verhalten würde.
Es existierten drei unterschiedliche Thesen (Abb. 8.1). Lord Kelvin
vertrat die Ansicht, dass die Elektronen am Nullpunkt an Ort und
Stelle einfrören und demnach der Widerstand gegen Unendlich strebt.
Der deutsche Physiker Matthiesen glaubte, es verbleibe ein konstanter
Restwiderstand in den Metallen. Onnes und Dewar dagegen
vermuteten, dass der Widerstand weiter linear abnimmt.
Abb. 8.1:
Theorien zum Verhalten von Metallen nahe dem absoluten Nullpunkt.
188
Ingenieurkeramik III
Da gewöhnlich Verunreinigungen in Metallen ihre elektrische
Leitfähigkeit beeinträchtigen und somit die experimentellen Resultate
verfälschen, arbeitete Onnes mit Quecksilber (es lässt sich leicht
reinigen, da es bei RT flüssig ist). Zunächst beobachtete er wie
erwartet eine kontinuierliche Abnahme des Widerstandes. Bei 4.2 K
schien aber der Widerstand vollständig verschwunden zu sein. Diese
Messung erweckte vorerst keineswegs Entdeckerglück, sondern vor
allem Misstrauen gegenüber der Messmethode und den Messgeräten.
Durch wiederholte Versuche überzeugte er sich schliesslich, dass
tatsächlich stets ein Sprung im Widerstand des Quecksilbers auftrat
(Abb. 8.2). Experimente mit Zinn und Blei zeigten bald, dass auch
andere Metalle bei ausreichender Kühlung supraleitend werden. Für
seine Leistung bei der Erforschung des Verhaltens von Metallen in der
Nähe des absoluten Nullpunktes wurde Onnes im Jahre 1913 der
Nobelpreis verliehen.
Abb. 8.2:
Der elektrische Widerstand von Hg als Funktion der Temperatur.
Während den folgenden 75 Jahren wurden zwar einige wenige
Anwendungen entwickelt, wie z. B:
• Leistungsfähige supraleitende Magnete für MRI (magnetic
resonance imaging) in der Medizin.
• Hochfeldmagnete in hochenergetischen Teilchenbeschleunigern.
• Sehr sensible magnetische Felddetektoren - SQUID’s
(Superconducting Quantum Interference Devices).
Aber die notwendige Kühlung mit flüssigem Helium verhinderte aus
wirtschaftlichen Gründen eine breitere Anwendungspalette.
Im April 1986 entdeckten K.A. Müller und J.G. Bednorz (zwei
Forscher bei IBM in Zürich) Supraleitung im System (LaBa)2CuO4,
Ingenieurkeramik III
welches schon bei einer Temperatur von 35 K supraleitend wurde. Für
diese Entdeckung wurde ihnen der Nobelpreis verliehen.
Nur wenige Monate später entdeckte eine Gruppe aus Houston
Supraleitung bei Temperaturen über 77 K (flüssigem Stickstoff) in
YBa2Cu3O(7-δ) . Dies eröffnete völlig neue Perspektiven, da Kühlung
mit Stickstoff sowohl um Grössenordnungen billiger als auch viel
einfacher zu handhaben ist.
Das Rennen um die Entdeckung weiterer supraleitender Materialien
mit noch höheren Sprungtemperaturen begann. 1988 wurden
Supraleiter im Bi-Sr-Ca-Cu-O-System (TC = 110 K) und im Tl-Ba-CaCu-O-System (TC = 125 K) gefunden. Im Jahre 1993 wurde
schliesslich an der ETH Zürich im System Hg-Ba-Ca-Cu-O
Supraleitung mit TC = 133 K gefunden. Die gleiche Verbindung unter
Hochdruck hergestellt erreicht ein TC > 150 K, was bis heute die
höchste gemessene Sprungtemperatur geblieben ist.
Die Entdeckung der Supraleitung oberhalb von 77 K in einer so
speziellen Materialgruppe wie den keramischen Oxiden forderte
Physiker, Chemiker und Materialwissenschaftler gleichermassen. Das
Überdenken der bisherigen Theorien sowie die Begründung und die
Konsequenzen neuerer Beobachtungen waren und sind immer noch
eine grosse Herausforderung der Wissenschaft. Obwohl 1987 die
„flüssig Stickstoff - Barriere“ durchbrochen worden ist, sind viele
grosse Versprechungen der Supraleitertechnologie bis heute noch
nicht realisiert worden. Viele technische Probleme verhindern den
Einsatz in vielerlei Anwendungen. Falls die Sprungtemperatur noch
weiter erhöht werden kann (bis RT ?), ist sicher auch eine Revolution
der gesamten bisherigen Technologie möglich.
Techniker in aller Welt träumen schon von supraleitenden Antrieben
für Magnetschwebebahnen, Schiffe oder gar Kraftfahrzeuge, Geräte
vom einfachen Sensor bis hin zum supraleitenden Grosscomputer und
Systemkomponenten vom Kabel bis zum Generator. Die Entwicklung
wird sicherlich noch einige Jahrzehnte oder mehr dauern, sofern sich
die materialtechnischen Probleme überhaupt lösen lassen.
189
190
Ingenieurkeramik III
8.1 Was ist Supraleitung?
Onnes entdeckte 1911, dass der elektrische Widerstand von
Quecksilber beim Abkühlen unter 4.2 K sprungartig auf Null abfällt
(Abb. 8.2). Ob allerdings tatsächlich R = 0 gilt, kann experimentell
nicht bestimmt werden. Als untere Grenze des Widerstandsprunges
gilt heute ein Abfall um mindestens vierzehn Zehnerpotenzen. In
einem Experiment, floss ein induzierter Strom im Ring aus einem
Supraleiter ohne messbare Verminderung während zweieinhalb
Jahren! Ein Supraleiter hat einen spezifischen Widerstand, der
mindestens 1017-mal kleiner ist als derjenige von Kupfer. Wir können
also getrost sagen: unterhalb einer kritischen Temperatur kann ein
supraleitender Zustand auftreten, wobei der elektrische Widerstand
Widerstand / m
0.010
onset
0.008
0.006
Abb. 8.3:
Verschiedene Definitionen von TC .
0.004
R=0
0.002
0.000
80
90
100
110
120
Temperatur / K
verschwindend klein wird. Zu beachten gilt es, dass die Bedingung R
= 0 nur für Gleichstrom gilt. Die Beschreibung des Widerstandes bei
Wechselstrom ist sehr komplex und sprengt den Rahmen dieses
Kapitels.
Wie schon in der Einleitung taucht im Zusammenhang mit
Supraleitung immer wieder der Begriff kritische Temperatur oder
Sprungtemperatur TC auf. Diese definiert den Phasenübergang
zwischen normal- und supraleitendem Zustand. Tc,onset ist die
Temperatur bei welcher der Widerstand beim Abkühlen vom linearen
Verhalten abweicht und unterhalb von Tc,R=0 ist kein Widerstand
mehr messbar (Abb. 8.3). Dazwischen sind weitere Definitionen
gebräuchlich, z.B. ist TC,50 diejenige Temperatur, bei welcher der
Widerstand auf die Hälfte abgesunken ist.
Im Jahr 1933 konnten Meissner und Ochsenfeld zeigen, dass der
supraleitende Zustand neben der Eigenschaft R = 0 zusätzlich die
Eigenschaft hat, ein Magnetfeld immer aus seinem Innern zu
verdrängen; das Material erweist sich als perfekter Diamagnet.
Dieser Effekt wird heute kurz Meissner-Effekt genannt: B = 0. An
Ingenieurkeramik III
191
der Oberfläche des Supraleiters (T<TC) werden supraleitende
Abschirmströme angeworfen, welche ein Magnetfeld erzeugen, dass
im Inneren des Supraleiters das äussere Magnetfeld exakt
kompensiert.
Bi > 0, T > TC
Bi = 0, T < TC
Abb. 8.4.:
Schematische Darstellung des Meissner - Effekts in einer supraleitenden Kugel, die
bei konstantem äusserem Magnetfeld abgekühlt wird. Beim Unterschreiten der
Sprungtemperatur werden die Induktionsfeldlinien aus der Kugel herausgedrängt.
Abb. 8.5:
Spezifische Wärme eines Supraleiters.
In Festkörpern werden die Beiträge zur spezifischen Wärme cP von
Phononen (Gitterschwingungen) und Elektronen geliefert. Im
normalleitenden Zustand gilt:
cPhononen ~T³ und cElektronen ~T.
Nach dem Übergang zur supraletenden Zustand gilt:
cElektronen ~exp(-C/T) ,
was zu einem Sprung in der spezifischen Wärme führt (Abb. 8.5).
192
Ingenieurkeramik III
8.2 Supraleitende Werkstoffe
Die Antwort auf die Frage, welche Werkstoffe supraleitende
Eigenschaften zeigen, soll hier in zwei Teilen gegeben werden. Es ist
naheliegend, dass als erstes die Elemente als Reinstoffe untersucht
wurden, ehe man sich an deren Verbindungen und Legierungen wagte.
8.2.1
Supraleitende Elemente
Abb. 8.6:
Periodensystem der supraleiten-den Elemente.
•Die ferromagnetischen Elemente ((Fe, Co, Ni) sind nicht supraleitend
•Die guten Leitern (Ag, Cu, Au..) sind keine Supraleiter•Nb zeigt das
höchste TC = 9.2K aller Elemente
8.2.2
Supraleitende Verbindungen
Es sind weit über tausend supraleitende Legierungen und
Verbindungen bekannt. Man findet sogar supraleitende Verbindungen,
für deren Komponenten keine Supraleitung beobachtet wird. Als
Beispiel hierzu sei CuS mit TC = 1.6 K erwähnt.
Eine interessante Gruppe bilden die Supraleiter
Wolframstruktur vom Typ Nb3Sn, Nb3Ga, Nb3Ge.
mit
β-
Ingenieurkeramik III
193
Ge
Nb
Abb. 8.7:
Elementarzelle der
β-Wolframstruktur
Charakteristisch für diese Struktur ist die Anordnung der Nb-Atome in
Ketten parallel zur x-, y- und z-Achse. Diese orthogonalen Ketten
schneiden sich nicht. In den Ketten haben die Nb-Atome einen
kleineren gegenseitigen Abstand als im Gitter des reinen Nb. Die
Kettenstruktur scheint hierbei für die besonderen Eigenschaften
verantwortlich zu sein.
Abb. 8.8:
Supraletende Verbindungen
Verbindung
Nb3Sn
Nb3Ge
PbMo6S8
NbO
NaxWO3
BaPb1-xBixO3
(LaSr)2CuO4
YBa2Cu3O7-x
HgBa2Ca2Cu3O8+x
K3C60
Cs2RbC60
TC [K]
18
Tieftemperatur
Supraleiter
23
15
Cheverel Phase
2
Tieftemperatur
oxydische
6
Supraleiter
12
Hochtemperatur
36
Supraleiter
93
135
19
Fullerene
33
Die Hypothese, wonach es möglich sein sollte, organische Supraleiter
mit besonders hohem TC zu finden, war bereits 1964 formuliert
worden. Aber erst im Jahre 1980 wurde von Jerome et al. der erste
organische Supraleiter entdeckt. Inzwischen erreicht man
beispielsweise mit der Verbindung (BEDT-TTF)2Cu(CNS)2
Übergangstemperaturen von 10.4 K. Mit der Entdeckung der
Fullerene 1990 wurden diese kritischen Temperaturen bei weitem
übertroffen. Für die Zusammensetzung Cs2RbC60 wurde ein
maximales TC von 33 K gemessen.
194
Ingenieurkeramik III
Abb. 8.9:
Struktur eines C60-Fullerens
Vor mehr als 20 Jahren stellten A. Sleight und seine Mitarbeiter beim
amerikanischen Chemiekonzern Du Pont einen keramischen
Werkstoff aus Barium, Blei, Wismut und Sauerstoff her. Obwohl
seine Sprungtemperatur bei nur 12 K lag, brachte er J.G. Bednorz und
K.A. Müller auf die Idee, gezielt nach keramischen Supraleitern zu
suchen. Sie leiteten im September 1986 durch ihren Artikel in der
Zeitschrift für Physik B die Revolution in der Supraleiterforschung
ein.
Proben aus dem La-Ba-Cu-O-System zeigten bereits bei 34 K einen
steilen Abfall des elektrischen Widerstandes. Mit dem Nachweis des
Meissner-Effektes war der Beweis für die Supraleitung der Proben
erbracht. Dies löste einen wahren „Goldrausch“ nach oxidischen
Supraleitern aus. Bereits einige Monate später wurde von Y-Ba-Cu-O
berichtet, bei dem TC-Werte > 92 K beobachtet wurden. 1988 wurden
Supraleiter im Bi-Sr-Ca-Cu-O-System (TC = 110 K) und im Tl-Ba-CaCu-O-System (TC = 125 K) gefunden.
Über Ostern 1993 entdeckte A. Schilling von der ETH Zürich
Supraleitung im Hg-Ba-Ca-Cu-O-System bei 133 K. Ähnliche
Verbindungen unter Hochdruck synthetisiert gaben Spitzenwerte bis
zu 157 K. Dieser Erfolg entbehrt freilich nicht einer gewissen Ironie.
Schon der vorherige Rekordhalter Tl-Ba-Ca-Cu-O enthielt mit
Thallium ein hochgiftiges Element, das seine kommerziellen
Ingenieurkeramik III
Einsatzmöglichkeiten einschränkt. Mit Quecksilber ist auch der neue
Rekordhalter nicht ungefährlich. Es scheint, als reiche die Natur den
Gral der Höchsttemperatur-Supraleitfähigkeit nur als Giftbecher.
Diese oxidischen Supraleiter - die sogenannten HochtemperaturSupraleiter (HTSL) - stehen zur Zeit im Brennpunkt des
Forschungsinteresses aller Industrienationen.
Abb. 8.10:
Historische Entwicklung der kritischen Temperatur.
8.3 Die Physik der Supraleitung
Die Theorie der Supraleitung ist extrem kompliziert und benötigt das
Verständnis der Quantenmechanik. Die ausführliche und vollständige
Diskussion über die Quantenmechanik der Supraleitung sprengt den
Rahmen dieses Kapitels. In diesem Abschnitt sollen nur einige
Grundlagen vermittelt werden.
Supraleiter haben die Eigenschaft, Gleichstrom ohne elektrischen
Widerstand zu leiten. Die Elektronen wandern demnach ungehindert
durch das Kristallgitter; denn jede Art von Zusammenstössen
verursacht Reibung und somit Energieverluste. Die Fähigkeit der
Elektronen ungehindert durch das Material zu wandern hat die
Wissenschaftler über viele Jahre beschäftigt. Die drei amerikanischen
Physiker J. Bardeen, L. Cooper, und J. Schrieffer, lieferten mit der
195
196
Ingenieurkeramik III
BCS-Theorie 1957 die erste mikroskopische Erklärung für die
Supraleitung. Sie erhielten für ihre Entdeckung 1972 den Nobelpreis.
Nach dieser Theorie sind die Elektronen bei tiefer Temperatur
gepaart. Die Kopplung zwischen ihnen beruht auf ihrer
Wechselwirkung mit dem Kristallgitter. Ein Elektron, das an den
Ionen des Gitters vorbeiwandert, kann dessen Lage verschieben.
Dieses Elektron erzeugt ein Phonon (Abb. 8.11).
Abb. 8.11:
Schematische Darstellung der
Gitterdeformation durch einem
Elektron.
Die Verformung des Gitters bildet eine Region mit positiver
Ladungsdichte, die wiederum ein zweites Elektron anzieht. Während
einer Phononoszillation kann das Elektron eine Distanz von ~104Å
zurücklegen. Das zweite Elektron wird dann angezogen ohne die
Abstossungskraft des ersten Elektrons zu spüren. Zwischen den
beiden Elektronen entsteht also eine Anziehung, die bei niedrigen
Temperaturen stärker ist als die Coulomb-Abstossung. Die beiden
Elektronen bilden also einen gebundenen Zustand, und man spricht
von einem Cooper-Paar (Abb. 8.12).
Abb. 8.12:
Schematische Darstellung derElerktron-Phonon-Wechselwirkung, welche für die
Bildung der Cooper-Paare vearantwortlich ist.
Ingenieurkeramik III
Die Elektronen in Cooper-Paaren haben entgegengesetzte Spins, so
dass sie als ein Teilchen mit Gesamtspin null betrachtet werden.
Solche Teilchen mit geradzahligem Spin bezeichnet man als Bosonen.
Für sie gilt, dass ein Quantenzustand je wahrscheinlicher ist, desto
häufiger er bereits besetzt ist, d.h. die Bosonen nehmen alle den
selben Quantenzustand mit gleicher Energie ein (Abb. 8.13). Für
Fermionen, Teilchen mit halbzahligem Spin (z.B. Elektronen), gilt
hingegen das Pauliverbot wonach jeder Quantenzustand nur einmal
besetzt wird. Im Grundzustand des Supraleiters bei T = 0 K sind
sämtliche Elektronen in Cooper-Paaren gebunden, die alle die gleiche
Energie haben. Die Impulse der einzelnen Elektronen sind bei T = 0 K
gleich gross, aber entgegengesetzt.
Abb. 8.13: Bose and Fermie Statistik
Die bisher besprochenen Cooper-Paare haben keinen Impuls. Somit
bewegen sich gleich viele Elektronen in die eine wie in die andere
Richtung, und es fliesst kein Strom. Wird dem System, z.B. durch
Anlegen einer Spannung, Energie zugeführt die kleiner ist als die
Bindungsenergie der Paarkorrelation, so bleiben die Cooper-Paare
erhalten, besitzen aber einen von null verschiedenen Gesamtimpuls.
Alle Cooper-Paare haben dabei den gleichen Impuls: Im Supraleiter
fliesst ein Strom. Ein normaler Leiter hat einen Widerstand, weil der
Impuls der Ladungsträger bei deren Streuung am Atomrumpfgitter
verändert wird. Wie besprochen, tritt die Streuung an
Verunreinigungen (Fremdatomen) oder an thermischen Schwingungen
der Gitterionen (Phononen) auf. In einem Supraleiter werden die
Cooper-Paare fortwährend aneinander gestreut; jedoch bleibt bei
diesem Vorgang der Gesamtimpuls erhalten, so dass sich keine
Änderung des Stromes ergibt. Ein Cooper-Paar kann nicht an einem
Atomrumpf gestreut werden, weil dies einen Energieverlust zur Folge
hätte was für ein Boson nicht möglich ist. Der einzige Weg, den Strom
durch Streuung zu verringern, besteht darin, die Bindung der CooperPaare aufzubrechen. Dies erfordert eine kinetische Energie der
Cooper-Paare die gleich oder grösser als die Bindungsenergie der
Paarkorrelation ist. Bei kleinen Strömen sind Streuvorgänge, bei
denen sich der Gesamtimpuls eines Cooper-Paares ändert, völlig
ausgeschlossen. Daher haben Supraleiter keinen Widerstand.
197
198
Ingenieurkeramik III
Man darf bei der beschriebenen Modellvorstellung nicht vergessen,
dass es sich bei der Paarbildung um einen dynamischen Prozess
handelt, da sich die Elektronen durch das Gitter bewegen.
Ausschlaggebend ist letztlich die Geschwindigkeit, mit der das Gitter
der Störung durch ein vorüberfliegendes Elektron folgen kann und
somit die Eigenfrequenz des Gitters.
Die guten elektrischen Leiter werden nicht zu Supraleiter. Beim
guten Leiter ist die Wechselwirkung zwischen Elektronen und dem
Gitter schwach. Für die Supraleiter ist die Elektron-Phonon-Kopplung
wichtig.
Die C-Paarbildung wird über eine Gitterschwingung vermittelt. Diese
Schwingung wird von der Masse der schwingenden Gitterionen
abhängig. Das führt zur einer Verschiebung der TC wenn Elemente
mit unterschiedlichen Massen (Isotope) in das Gitter eingebaut
werden (Isotopieeffekt).
TC~M-α
Für viele Tieftemperatur- Supraleiter α=0.5
Abb. 8.14:
Isotopieeffekt in Hg
Spezifische Wärme
In den Supraleiter führt die Bildung der Cooper-Paaren zur einer
Änderung der Zustandsenergieverteilung in der Nähe der
Fermieenergie EF. Unterhalb der TC bildet sich um die Fermieenergie
eine Energielücke 2Δ. Die Cooper-Paare im Grundzustand haben die
Energie um Δ kleiner als die EF. Die ungepaarten Elektronen (oder
zerrissene Cooper-Paare) haben eine höhere Energie EF+Δ. Mit der
Erhöhung der Temperatur wird 2Δ immer kleiner und bei TC gleich
Null. Zugleich werden alle Cooper-Paare zerrissen. Die 2Δ Werte
könnte man aus den Messungen der spezifischen Wärme entnehmen
(Abb. 8.15)
SL
cEleS ~exp(-Δ/kT)
NL
Temperatur
Abb. 8.15:
Energielücke und spezifische
Wärme in Supraleiter
TC
cElektronen ~exp(-Δ/kBT) ,
kB - Boltzmannkonstante2Δ=Eg – Energielüke. Cooper-Paare
Bindungsenergie.
Ingenieurkeramik III
Die BCS Theorie gibt eine universelle Abhängigkeit zwischen der
Energielücke und TC.
2Δ=3.5kBTC
Tc<20K Eg~1meV
Tc~100K Eg~5meV (Eg≈1.2eV für Si)
Zu beachten gilt es, dass diese Beschreibung, basierend auf der BCSTheorie nur auf Tieftemperatur-Supraleiter (TTSL) anwendbar ist.
Eine Theorie, die das Phänomen der Hochtemperatur-Supraleitung
zufriedenstellend erklärt, gibt es zur Zeit noch nicht.
199
200
Ingenieurkeramik III
8.4 Supraleiter im „Phasenraum“ Temperatur –
Strom - Magnetfeld
Wir haben bis jetzt gesehen, dass Supraleitung nur unterhalb einer
kritischen Temperatur TC möglich ist. Gleichzeitig wissen wir, dass
ein äusseres Magnetfeld vom Supraleiter verdrängt wird. Es ist
anzunehmen, dass auch hier eine kritische obere Grenze besteht;
oberhalb eines kritischen Magnetfeldes wird dieses in den
Supraleiter eindringen und den supraleitenden Zustand zerstören. Um
den verschwindenden elektrischen Widerstand auszunützen, wollen
wir verlustfrei Strom transportieren. Dabei ist zu beachten, dass jeder
Strom ein Magnetfeld aufbaut. Z.B. erzeugt ein Strom I durch einen
langen, dünnen Draht ein Feld, dessen Feldlinien konzentrische Kreise
bilden und dessen magnetische Flussdichte B im Abstand R vom
Leiter gegeben ist durch:
I
B = μ0 ⋅
2 πR
(8.1)
Damit stellen sich zwei Probleme:
1. Wie kann das durch den Stromfluss zwingend erzeugte Magnetfeld
im Supraleiter verpackt werden, wo doch dieser Magnetfelder aus
seinem Inneren verdrängen will?
2. Die Supraleitung bricht spätestens dann zusammen, wenn das
durch den Stromfluss erzeugte Magnetfeld den kritischen Wert
übersteigt. Somit gibt es also eine kritische Stromdichte jC.
Wir haben festgestellt, dass neben der kritischen Temperatur TC auch
ein kritisches Magnetfeld BC und eine kritische Stromdichte jC
existieren. Die Supraleitung tritt nur auf wenn alle 3 Grössen, die
voneinander abhängig sind, unterschritten werden – wir sprechen von
einem Phasenraum über T-j-B.
Um Verwechslungen vorzubeugen werden in der Folge
Magnetfelder durch ihre magnetische Induktion B
charakterisiert.
Es gilt im Vakuum:
B = μ0 ‚ H
und innerhalb einer Substanz:
B = μ0 ‚ (H+M)
Ingenieurkeramik III
Abb. 8.16:
Der supraleitende Phasenraum
201
202
Ingenieurkeramik III
8.5 Die London-Gleichungen, Eindringtiefe und
Kohärenzlänge
Eine erste phänomenologische Theorie zur Supraleitung wurde von F.
und H. London vorgeschlagen. Analog zum Ohm’schen Gesetz
j = σ‚E im normalleitenden Fall wurde eine Verknüpfung der
Stromdichte mit dem elektrischen Feld (R = 0 im supraleitenden
Zustand) gesucht.
Abweichend vom normalen Fall (Ohm’sches Gesetz) bei welchem die
Geschwindigkeit der Elektronen im E-Feld konstant ist (die
Proportionalitätskonstante heisst spez. Widerstand) ist beim
Supraleiter der Widerstand = 0. Die Ladungsträger werden also
ständig beschleunigt und dies proportional zum Feld E.
Die erste Londonsche Gleichung beschreibt Widerstadlosesbehalten
von Supraleitern:
Die Bewegungsgleichung für Elektronen im elektrischen Feld lautet,
dJ/dt=E⋅n⋅e2/m
m…
n…
e…
E…
Ladungsträgermasse
Ladungsträgerdichte
Ladung von Elektron
Elektrische Feldstärke
(8.2)
Die zweite Londonsche Gleichung beschreibt den exponentiellen
Abfall des B-Feldes von der Supraleiteroberfläche ins Innere
B=B0⋅exp(-x/λ)
(8.3)
Dabei bezeichnet λ die Stelle, wo B(x) auf den e-ten Teil des
Oberflächenwertes abgefallen ist. Man nennt λ die Londonsche
Eindringtiefe. Sie ist temperaturabhängig, da die Ladungsträgerdichte
n temperaturabhängig ist. Dabei gilt ungefähr λ(T) = λ0‚(1-(T/TC)4)-0.5.
Wie in Abb. 8.17 ersichtlich, steigt die Eindringtiefe gegen TC hin
stark an, das Magnetfeld dringt immer mehr ein und zerstört die
Supraleitung.
Ingenieurkeramik III
203
Abb. 8.17
Abb. 8.18
Abb. 8.17:
Temperaturabhängigkeit der Londonschen Eindringtiefe λ des äusseren Feldes in
die Oberfläche eines Supraleiters.
Abb. 8.18:
Eindringtiefe und Dichte der Cooper-Paare an der Grenzfläche normal- Æ
supraleitend.
In Abb. 8.18 ist dargestellt, wie das Magnetfeld in den supraleitenden
Querschnitt eindringt. Gleichzeitig ist eingezeichnet, wie sich die
Dichte der supraleitenden Ladungsträger von Null am Rand auf nC
steigert.
Über die Kohärenzlänge ξGL (GL weist auf die Ginzburg-Landau
Theorie hin) ist definiert, innert welcher Distanz diese Dichte um den
e-ten Teil zunimmt. Man kann aber auch sagen:
− ξGL gibt den Abstand an, über den die Korrelation zu CooperPaaren wirksam ist. Anders ausgedrückt: Sie bezeichnet die grösste
nichtsupraleitende Strecke (Korngrenze, Verunreinigung), die ein
Cooper-Paar durchtunneln kann oder den Abstand zwischen den
beiden Elektronen eines Cooper-Paares (Abb. 8.19).
CooperAbb. 8.19:
Tunneleffekt und Weak links beim
Übergang Supraleiter – Normalleiter - Supraleiter.
ξGL
SL
NL
SL
x
ξGL > x Æ
SL
NL
SL
x
ξGL < x Æ Weak link
204
Ingenieurkeramik III
− ξGL gibt auch die kleinste Länge an, über welche die Dichte der
Cooper-Paare variieren kann.
Die Kohärenzlänge hat damit wesentlichen Einfluss auf die
elektrischen Eigenschaften des Supraleiters.
8.6 Josephsoneffekt
Metall-Isolator-Metall Tunneleffekt
Nehmen wir an, wir haben zwei Metallstücke die mit einer sehr
dünnen isolierenden Schicht getrennt werden; dann können die
Elektronen durch diese Barriere nicht fliessen. Legt man aber ein
Potenzial an, werden die Elektronen an einer Seite des Überganges
eine grössere Energie als an der anderer haben. Man bekommt an
beiden Seiten des M-I-M-Überganges unterschiedliche Fermi
Niveaus. Die isolierende Barriere könnte dann durchtunnelt werden.
Der Tunnelstrom wird in diesem Fall linear vom Potenzial (der
Spannung) abhängig.
Abb. 8.20:
Der Tunneleffekt und die Strom-Spannung Charakteristik beim Metall-IsolatorMetall Übergang
Metall-Isolator-Supraleiter Tunneleffekt
Wenn es an einer Seite des Überganges einen Supraleiter (bei
Temperatur unterhalb der TC) gibt, dann gibt es für den Supraleiter
eine Energielücke 2Δ in der Elektronen Zustandsenergieverteilung.
Die Zustände unterhalb der Energielücke sind mit Cooper-Paaren
Ingenieurkeramik III
besetzt. Die Elektronen aus dem Metall können in den unteren
Energieband nicht durchtunneln. Man muss wieder ein Potenzial
anlegen (und zwar grösser als Δ/e) um die Fermieenergie der MetallElektronen so zu erhöhen, dass sie in den Energieband oberhalb der
Lücke durchtunneln können. Die Strom-Spannungs Charakteristik ist
nicht mehr linear. Es fliesst kein Strom im Übergang bis die Spannung
den Wert Δ/e erreicht. Wenn die Spannung den Wert Δ/e
überschreitet, wird sofort ein sehr grosse Tunnelstrom durch den
Übergang fliessen.
Abb. 8.21:
Der Tunneleffekt und die Strom-Spannungs Charakteristik beim Metall-IsolatorSupraleiter Übergang
Supraleiter-Isolator-Supraleiter Tunneleffekt
Wenn der Übergang nicht polarisiert ist (d.h. ohne Spannung) können
die Cooper-Paare durch die isolierende Barriere tunneln. Das ist aber
nur dann möglich wenn die Dicke der Barriere kleiner ist als die
Kohärenzlänge. So kann der Strom über die Barriere ohne Verluste
(Wiederstand gleich Null) fliessen. Der maximale Strom der durch
den Übergang fliessen kann (Kritischer Josephson Strom) kann die
Werte 1-103 A/cm2 erreichen.
Mit einer Erhöhung der Spannung könnte man ähnliche Tunneleffekte
wie beim Metall-Isolator-Supraleiter Übergang erreichen. Man muss
aber eine Spannung anlegen die den Wert 2Δ/e überschreitet. Die
Cooper-Paare werden dann zerrissen und durchtunneln in den Band
oberhalb der Energielücke.
205
206
Ingenieurkeramik III
Abb. 8.22:
Der Tunneleffekt und die Strom-Spannung Charakteristik beim Supraleiter-IsolatorSupraleiter Übergang
8.7 Supraleiter im äusseren Magnetfeld
Wie bereits vorher angedeutet, ist das Verschwinden des elektrischen
Widerstandes nicht die einzige charakteristische Eigenschaft des
supraleitenden Zustandes. Der Meissner-Effekt der das Verhalten in
einem äusseren Magnetfeld beschreibt, insbesondere das Verdrängen
des Magnetfeldes aus dem Inneren einer supraleitenden Probe, kommt
noch dazu. Dabei kann man zwei grundsätzlich verschiedene
Verhaltensweisen beobachten, die von Ginzburg-Landau Parameter
κ=λ/ξGL abhängig sein.
8.7.1
Supraleiter 1. Art (Typ I)
Die Materialien für die κ<1/√2=0.71 nennt man Supraleiter Typ I.
Abb. 8.23:
Supraleiter Typ I. Kohärenzlänge ξ
und Eindringtiefe λ.
Ingenieurkeramik III
207
TC [K]
1.2
3.7
7.2
Al
Sn
Pb
λ [nm]
16
34
37
ξGL [nm]
1600
230
83
κ
0.01
0.16
0.47
Wird um einen Supraleiter 1. Art ein äusseres Magnetfeld aufgebaut,
so wird dieses nicht in den Supraleiter eindringen können (ausser in
einem sehr kleinen Oberflächenbereich Abb. 8.23). In diesem
Oberflächenbereich werden Abschirmströme angeregt die im Inneren
des Supraleiters ein Feld aufbauen, das dem äusseren Feld exakt
entgegengesetzt ist. Die Summe der Felder im Supraleiter ist dann
gleich null. Man sagt, der Supraleiter ist ein perfekter Diamagnet.
Dieser Sachverhalt lässt sich auf zwei Arten darstellen. Abb. 8.24
zeigt die Magnetisierung der Supraleiter in Funktion des äusseren
magnetischen Feldes. Es ist darauf zu achten, dass die Magnetisierung
in negativen Einheiten aufgetragen wird! Diese Abbildung zeigt das
diamagnetische Feld, welches im Inneren aufgebaut wird, um das
äussere Feld zu kompensieren. Wie schon vorher angedeutet,
funktioniert dies nur bis zu einem kritischen Feld BC, dann bricht die
Supraleitung zusammen und das äussere Feld dringt vollständig ein.
Bc
Abb. 8.24
Abb. 8.25
Abb. 8.24:
Magnetisierungskurve eines Supraleiters 1. Art
Abb. 8.25:
Magnetfeld im Inneren eines Supraleiters 1. Art als Funktion des Aussenfeldes.
Es gilt Bi = Ba + μ0‚ M = 0 im supraleitenden und Bi = Ba im
normalleitenden Zustand.
Die zweite Möglichkeit der Darstellung ist in Abb. 8.25 gezeigt. Hier
wird das resultierende Feld im Inneren des Supraleiters als Funktion
des Aussenfeldes aufgetragen. Solange das externe Feld kleiner als BC
208
Ingenieurkeramik III
bleibt, ist die Probe supraleitend und das Innenfeld gleich Null.
Sobald die Supraleitung zusammenbricht, dringt das Aussenfeld ein
und das Innenfeld entspricht dem Aussenfeld.
Solche Supraleiter 1. Art sind technologisch uninteressant, da sie nur
in einer dünnen Oberflächenschicht Stromtransport erlauben.
8.7.2
Supraleiter 2. Art
Die Materialien für die κ>0.71 nennt man Supraleiter Typ I.
Die HTSL zeichnen sich durch extrem kurze Kohärenzlängen aus. In
Abb. 8.26:
Supraleiter Typ II. Kohärenzlänge ξ
und Eindringtiefe λ.
den Schichtebenen betragen sie 1 bis 4 nm, senkrecht dazu weniger
als 1 nm, damit liegen sie etwa um das hundertfache niedriger als in
den TTSL.
TC [K]
λ [nm] ξGL [nm] κ
Nb
9.3
39
38
1
Nb3Sn
18
80
3
27
YBa2Cu3O7
93
150
1.5
100
Rb3C60
30
247
2.0
124
Bi2Sr2Ca2Cu3O10
110
200
1.4
143
In Supraleitern 2.Art ist es energetisch günstiger, wenn ein
ansteigendes äusseres Magnetfeld nicht vollständig bis zum Kollaps
verdrängt wird, sondern „portionenweise“ in die supraleitende
Struktur eindringen kann.
Die Magnetisierungskurve eines solchen Supraleiters 2. Art ist in Abb.
8.27 gezeigt. Kleine externe Felder werden wie im Supraleiter 1. Art
vollständig kompensiert (verdrängt), so dass die Magnetisierung linear
mit dem äusseren Feld ansteigt. Ab einer gewissen Grenze BC1 nimmt
die Magnetisierung der supraleitenden Probe eher langsam ab bis sie
bei BC2 vollständig verschwindet.
Ingenieurkeramik III
Abb. 8.27:
Magnetisierungskurve eines Supraleiters 2. Art
Abb. 8.28:
Mittleres Magnetfeld im Inneren eines Supraleiters 2. Art als Funktion des
Aussenfeldes
Die Grösse des mittleren Innenfeldes ist in Abb. 8.28 gezeigt. Zu
Beginn bleibt es Null, steigt dann ab BC1 stetig an bis bei BC2 das
Aussenfeld vollständig eingedrungen ist.
Das stufenweise Eindringen des Magnetfeldes in den Supraleiter
geschieht in Form einzelner Flussquanten, die man auch als
Flussschläuche, -linien oder -fäden bezeichnet. Diese Flussschläuche
ordnen sich in einem hexagonalen Gitter an, da für diese Anordnung
die Enthalpie minimal ist. Die Abstände ergeben sich dadurch, dass
die für eine bestimmte Magnetfeldstärke zwischen BC1 und BC2
notwendige Anzahl Flussschläuche sich gleichmässig über die zur
Verfügung stehende Fläche verteilen. Es ist gelungen, die Lage der
einzelnen Flussschläuche mit Eisenkolloid zu markieren und so
sichtbar zu machen. Mittels STM (Scanning Tunneling Microscopy)
können die Flusslinien auch visualisiert werden (Abb. 8.30). Es ist
dies der einzige makroskopisch sichtbare Quanteneffekt.
Der Durchmesser der Flussschläuche entspricht der Kohärenzlänge
ξGL. Im Inneren sind die Flussschläuche nicht supraleitend (nS→0
Abb.8.31) und das Magnetfeld (B) kann sie durchdringen. Ein
Supraleitender Strom ( Dichte jS) fliest um jeden Flussschlauch.
209
210
Ingenieurkeramik III
Abb. 8.29:
Flussliniengitter in einem Typ-II-Supraleiter. Jede magnetische Flusslinie trägt ein
elementares Flussquantum:
Φ0=h/2e≅2.07·10-15Tm2
Abb.8.30:
STM (Scanning Tunneling Microscopy) Aufnahme des Abrikosov-Gitters in NbSe2
Abb. 8.31:
Die Struktur der Flussschläuchen in Supraleiter Typ II
Während wir beim Supraleiter 1. Art nur die beiden Zustände
supraleitend (Meissner-Phase 0 < B < BC,th ) und normalleitend (BC,th
< B) vorgefunden haben, kommt beim Supraleiter 2. Art noch ein
Zwischenzustand, die sogenannte Gemischte Phase (BC1 < B < BC2)
hinzu.
Oberhalb eines Magnetfeldes BC1, bis zu welchem sich auch ein
Supraleiter 2. Art in der Meissner-Phase befindet, beginnt das äussere
Magnetfeld in das Innere des Supraleiters einzudringen und zwar mit
steigendem Aussenfeld. Erst oberhalb eines oberen kritischen Feldes
BC2 geht die Supraleitfähigkeit verloren. Erwähnenswert ist an dieser
Stelle noch, dass sich jeder Supraleiter 1. Art (es sind dies
Ingenieurkeramik III
211
ausnahmslos reine Elemente) durch Legieren in einen Supraleiter 2.
Art überführen lässt.
Abb. 8.32:
Unterscheidung von Supraleitern 1. und 2. Art im B-T-Diagramm.
1. Art: Hier tritt nur die Meissner Phase auf
2. Art: Hier tritt bei kleinen äusseren Feldern die Meissner Phase und bei höheren
die gemischte Phase auf.
8.7.3
Die kritische Stromdichte
Als kritische Stromdichte jC bezeichnet man die Transportstromdichte
für den ein Supraleiter unter gegebenen Bedingungen (äusseres
Magnetfeld und Temperatur) in den normalleitenden Zustand
übergeht.
JC ist für einen idealen Supraleiter durch BC1 bestimmt (vgl.
Phasendiagramm in Kapitel 8.7.2). BC1 ist das Magnetfeld, bei
welchem der Supraleiter für eine gegebene Temperatur von der
Meissner- in die Gemischte (Shubnikow)-Phase übergeht. Oberhalb
von BC1 dringt das Magnetfeld in Form von Flussschläuchen in den
Supraleiter ein. Die Wechselwirkung dieser Flussschläuche mit dem
Transportstrom führt zu einer Lorentzkraft, welche eine
Verschiebung der Flussschläuche durch den Supraleiter bewirkt.
fL = j × φ0
fL… Lorentzkraft pro Länge
φ0… Flussquant in Richtung von Ba
(8.4)
212
Ingenieurkeramik III
Abb. 8.33:
Wirkung der Lorentzkraft auf Flussschläuche in der Shubnikov-Phase.
Abb. 8.34:
Die Defekten im Kristallgitter (z.B. Verunreinigungen) die nicht supraleitend sind,
können die Flusslinien „verankern“. Das verhindert die Flusslinienbewegung,
solange die Stromdichte einen kritischen Wert jC nicht überschreitet
Für die Verschiebung der Flussschläuche genügt ein beliebig kleiner
Transportstrom. Diese Verschiebung verbraucht Energie, welche sich
in Form eines ohm'schen Verlustes bemerkbar macht. Die daraus
resultierende Erwärmung kann im Extremfall zur Zerstörung der
Supraleitung im gesamten Querschnitt führen. In einem idealen
Supraleiter 2.Art gibt es keine Kraft, welche der Lorentzkraft
entgegenwirkt. Man sieht sofort ein, dass für einen solchen Supraleiter
der kritische Strom oberhalb von BC1 Null ist.
Deshalb werden in der Praxis sogenannte harte Supraleiter
eingesetzt, wo das Wandern der Flussschläuche durch
Pinningzentren (Haftzentren) verhindert wird. Besonders wirksame
Hindernisse sind dabei normalleitende Ausscheidungen in der
supraleitenden Matrix. Je grösser diese Pinningzentren sind, desto
höher ist die Pinningkraft, die den Flussschlauch festhält, mindestens
aber sollten sie etwa so breit sein wie ein Flussschlauch um überhaupt
eine Haftwirkung zu erzielen. Neben der Beschaffenheit der
Pinningzentren wirkt sich auch die Steifigkeit der Flussschläuche auf
die Pinningkraft aus, je beweglicher sie sind desto schwieriger sind sie
zu pinnen.
Ingenieurkeramik III
Abb. 8.35:
Ein Hochtemperatur Supraleiter zeigt zwei Bereiche der gemischten (FLFlusslinien) Phase:
FL-Festkörper im Bereich Bc1(T)<B<Bm(T) sind die FL fest verankert.
FL bilden reguläres Abrikosov-Gitter. Der SL kann einen Transportstrom j<jc
verlustfrei tragen.
FL-Flüssigkeit. Die thermischen Fluktuationen „befreien“ die FL aus ihren
Verankerungen. Der SL zeigt einem elektrischen Widerstand.
Wird nun die Stromdicht, das Magnetfeld oder die Temperatur im
Supraleiter erhöht (und die Linie Bm(T) Abb. 8.35 überschriten), so
wird die Lorentzkraft, die Pinningkraft übertreffen und die
Flussschläuche losreissen. Der kritische Strom im Supraleiter wird
beim Flusslinienschmelzen scharf vermindern.
Abb. 8.36:
Leitfähigkeit des supraleitenden Materials gegenüber Temperatur bei unterschiedlichen
Magnetfeldern. Bei der Tm-Temperatur „schmilzt“ das Flusslieniengitter und die
Wiederstand des Materials nimmt zu.
213
214
Ingenieurkeramik III
8.8 Hochtemperatur Supraleiter (HTSL)
8.8.1
La2-xSrxCuO4
Die (LaBa)2CuO4 war die erste supraleitende Kupratverbindung die
von K.A.Müller und G. Bednorz 1986 synthetisiert wurde. Die TC
beträgt 35K. Noch höhere Werte erreicht man wenn Lanthan mit
Strontium (statt mit Barium) substituiert wird. Die kritische
Temperatur ist in dieser Verbindung von der Strontium- bzw.
Bariumkonzentration abhängig. Bei der Dotierung, werden statt
dreiwertigen Lanthankationen zweiwertige Strontium Katione in das
Gitter eingebaut. Die Sauerstoffleerstellen werden wiederum mit den
Sauerstoffatomen aus der Gas Phase besetzt. Die Löcher die dabei
entstehen können gehen dann in die CuO2-Schichten über.
x
2SrO → 2Sr‘La + 2O O + V··O
x
V··O+ 0.5O2→ O O+ 2h·Die Ladungsträger in La Sr CuO (auch bei
2-x
x
4
meisten anderen HTSL) sind deshalb Löcher.Es gibt eine optimale
Löcherkonzentration bei der die höchste TC-Werte erreicht werden
(Abb. 8.38)
Abb. 8.38:
Phasen-Diagram für La2-xSrxCuO4
Abb. 8.37:
Kristallstruktur des La2-xSrxCuO4
Ingenieurkeramik III
8.8.2
215
YBa2Cu3O7-x
Bis jetzt wurden viele Verbindungen hergestellt die noch höhere
Sprungtemperaturen als bei La2-xSrxCuO4 vorweisen. Es ist
charakteristisch, dass alle diese Verbindungen Perovskit ähnliche
Strukturen haben und enthalten Kupfer.
YBa2Cu3O7-x (Y123) war die erste Kupratverbindung deren
Sprungtemperatur oberhalb 77K (Flüssiger Stickstoff) liegt.
Abb. 8.39:
Kristallstruktur des YBa2Cu3O7-x
Abb. 8.40:
Kritische
Temperatur
YBa2Cu3O7-x
Die Synthese von YBa2Cu3O7-x ist relativ einfach. Man benutzte als
Ausgangsmaterialien Y2O3, BaCO3 und CuO. Die Synthese findet bei
~930oC statt:
0.5Y2O3 + 2Ba2CO3 + 3CuO + x/2O2→YBa2Cu3O7-x + 2CO2 + ΔH
Die kritische Temperatur für Y123 ist stark vom Sauerstoffgehalt
abhängig (Abb. 8.40). Der Sauerstoffgehalt für diese Verbindung ist
von der Temperatur (und Sauerstoffpartialdruck) abhängig.
Die Struktur sämtlicher keramischer Supraleiter ist geprägt durch
ihren schichtweisen Aufbau. Die Einheitszelle besteht aus
Kupferoxidschichten, die sich mit isolierenden Schichten abwechseln.
Die CuO-Schichten tragen den Suprastrom, während die isolierenden
für
216
Ingenieurkeramik III
Schichten den Elektronenhaushalt regulieren. Für die meisten
Hochtemperatur Supraleiter, die Löcher in den CuO2-Ebenen sind die
Ladungsträger. Die Elektronen werden von Kationen des
Ladungsreservoirs angezogen, was gleichzeitig eine Löcherdotierung
der CuO2-Ebenen verursacht.
8.3Å
Abb. 8.41:
Die Schichtstruktur der YBa2Cu3O7-x
Die Schichtstruktur ist auch für eine hohe Anisotropie der
physikalischen Eigenschaften verantwortlich. Entlang der c-Richtung
ist die Kohärenzlänge sehr klein (4Å in Y123). Deshalb können die
Cooper-Paare nicht die Ladungsreservoirs durchtunneln (Abb 8.42).
Der Superstrom fliesst nur entlang der CuO2-Schichten. Deshalb, für
Einkristalle YBa2Cu3O7 bei 4.2K, ist der kritische Strom entlang der
ab-Ebene 100 Mal grösser als entlang der c-Richtung
(jc(ab)~107A/cm2, jc(c)~105A/cm2).
ΤC
λab [Å] λc [Å] ξab [Å] ξc [Å]
YBa2Cu3O7
93
1500
6000
15
4
Bi2Sr2Ca2Cu3O10
110
2000
10000
13
2
Abb. 8.42:
Anisotropie der Eindringtiefe und Kohärenzlänge in YBa2Cu3O7-x und
Bi2Sr2Ca2Cu3O10.
Ingenieurkeramik III
8.8.3
217
Bi-Sr-Ca-Cu-O
Das dominierende Element in den isolierenden Schichten bestimmt
den Familiennamen der supraleitenden Verbindung (z.B. Bi-, Pb-, Hg, Tl- oder Cu-Supraleiter). Einen Sonderfall bilden die YBCOSupraleiter, die eigentlich zur Cu-Familie gehören, da ihre
isolierenden Schichten aus CuO-Ketten bestehen, aus historischen
Gründen aber als Yttrium-Supraleiter bezeichnet werden. Innerhalb
der entsprechenden Familien werden die Verbindungen nach der
Anzahl der Isolations- und CuO-Schichten unterschieden
Ca
Ca
Ca
Ca
Ca
Ca
Bi2Sr2CuO6 2201
TC=20K
Bi2Sr2CaCu2O8 2212
TC=95K
Bi2Sr2Ca2Cu3O10 2223
TC=110K
Abb. 8.43:
Strukturen A der Bi-Sr-Ca-Cu-Oxide Zusammensetzungen mit ihrer kritischen Temperatur
218
Ingenieurkeramik III
In Abb. 8.43 sind drei Beispiele aus der Bi-Familie aufgezeichnet, die
alle 2 isolierende Schichten aber eine, zwei oder drei CuO2-Schichten
beeinhalten. Die ausgeprägte Schichtstruktur der keramischen
Supraleiter dominiert auch deren Eigenschaften (z.B. TC).
Ähnlich wie bei Y123, sind die TC Werte von der
Sauerstoffkonzentration abhängig (Abb. 8.44).
Abb. 8.44:
TC Abhängigkeit von der Sauerstoffkonzentration in Bi2Sr2Ca1Cu2O10.
8.8.4
Hg-Ba-Ca-Cu-O
Quecksilbercuprate bilden eine ganze Reihe von Verbindungen die
Supraleitende Eigenschaften aufweisen. Die Mitglieder der
HgBa2Can−1CunO2n+2 „Familie“ unterscheiden sich an der Zahl der
CuO2-Schichten. Die Verbindung mit drei CuO2-Schichten
(HgBa2Ca2Cu3O8 -1223) hat seit 1993 einen Weltrekord bei der
Sprungtemperatur von 133K vorgewiesen.
Abb. 8.45:
Kristallstrukturen von HgBa2Can−1CunO2n+2 Verbindungen
Ingenieurkeramik III
219
Das Einbauen von mehreren CuO2-Schichten führt in die Struktur
zuerst zu einer Erhöhung der Sprungtemperatur. Die TC wird aber bei
mehr als drei Schichten wieder herabgesetzt (Abb. 8.46).
Abb. 8.46:
Die Abhängigkeit der Sprungtemperatur TC in HgBa2Can-1CunO2n+2 von „n“ Zahl derCuO2-Schichten.
8.8.5
HTSL: Wie geht es weiter?
Die HTSL unterscheiden sich wesentlich von „klassischen“
Supraleitern:
1. HTSL haben die Sprungtemperaturen die um 100K liegen. Aus
der BSC-Theorie könnte man erwarten, dass die maximale TC
30K nicht überschreitet.
2. Sauerstoff-Isotopeneffekt in Cupraten ist sehr klein. Für
YBa2Cu3O6.96 (optimal dotiert) αO=0.02 (TC=M-α).
Die BSC-Theorie kann die Eigenschaften von HTSL nicht
vollständig erklären. Es wird eine neue Erklärung für das
Phänomen der HTSL gesucht.
Die HTSL wurde nur in Cupratverbindungen gefunden. Sind die hohe
Sprungtemperaturen nur in Cupraten möglich?
Im Januar 2001 wurde eine Entdeckung der Supraleitung in MgB2 mit
der TC=39K veröffentlicht. Dies ist die höchste Sprungtemperatur die
für einen nichtcupratischen (und nicht oxydischen) Supraleiter
gemessen wurde. Die Verbindung hat eine interessante
Schichtkristallstruktur (Abb. 8.47). Die Boratomen bilden Schichten
die eine ähnliche Struktur hat wie die Kohlenstoffschichten in
Graphit.
Abb. 8.47:
Die Struktur von MgB2. Die BorAtome (kleine Kugeln) bilden
Graphitähnliche Schichten.
220
Ingenieurkeramik III
8.8.6
Technische Anforderungen
Ein Material muss verschiedene Kriterien erfühlen um eine
Anwendung zu finden. Im Fall der Supraleiter sind das vor allem:
•
•
•
•
•
Kritische Temperaturen über 77K
•Eine hohe kritische Stromdichte
•Ein hohes kritisches Magnetfeld•Eine einfache Herstellung
•Gute mechanische Eigenschaften
•Keine (oder kleine) Giftigkeit
Abb. 8.48:
Schematische Darstellung des
Stromflusses im polykrystallinen
Material.
Abb. 8.49:
Korngrenzenmodelle für
polykrystalischen HTSL.
Die Kohärenzlänge ξGL, die in Kapitel 8.5 definiert wurde, hat
verschiedene Bedeutungen. So entspricht sie sowohl der Strecke, die
ein Cooper-Paar durchtunneln kann, als auch der ungefähren Breite
eines Flussschlauches. Die HTSL zeichnen sich durch extrem kurze
Kohärenzlängen aus. Im polykristallinen Material tragen deshalb die
Korngrenzen
entscheidend
zu
einer
Verminderung
der
Stromtragfähigkeit bei. Andererseits wirken bereits kleinste
Verunreinigungen oder Ausscheidungen als Pinningzentren für die
Flussschläuche, weil diese sehr schmal sind. Trotz grösserer Anzahl
an Pinningzentren ist das Pinning in HTSL jedoch schlechter als in
TTSL, weil die Flussschläuche wegen der hohen Anisotropie in sich
viel beweglicher sind und deshalb ein einzelner Flussschlauch sehr
viel mehr Pinningzentren benötigt.
Der schichtartige Aufbau bringt es mit sich, dass die HTSL in
Plättchen auskristallisieren, mit einer Ausdehnung von etwa 100 μm
in ab-Richtung und von wenigen Mikrometern in c-Richtung. In
polykristallinem Material sind diese Plättchen statistisch angeordnet,
so dass sie sich nur an den Kanten berühren und Hohlräume
einschliessen. Die kleine Kohärenzlänge in c-Richtung erschwert es
den Cooper-Paaren, zwischen den CuO-Schichten hin und her zu
tunneln. Somit ist die Stromführung an die a-b-Ebenen gebunden. An
Ingenieurkeramik III
221
den Korngrenzen führt dies zu Schwierigkeiten, da die
stromführenden Ebenen selten von einem Korn ins nächste
durchgehen. Die elektrischen Verbindungen zwischen den Körnern
sind deshalb immer Tunnelkontakte. Man bezeichnet sie treffend als
"weak links", als schwache Glieder in den supraleitenden
Strompfaden. Jetzt können wir auch verstehen, warum es äusserst
wichtig ist, dass die Korngrenzen in HTSL möglichst sauber und
schmal sind: Je grösser die Strecke, die Cooper-Paare durchtunneln
müssen, desto unwahrscheinlicher wird dieses Durchtunneln. Wenn
also die Korngrenze dicker als die Kohärenzlänge ist, unterbricht sie
die supraleitenden Strompfade. Dies ist mit der Hauptgrund, warum
für die meisten supraleitenden Zusammensetzungen die kritischen
Stromstärken sehr gering sind, trotz TC über 100 K und genügend
vielen Pinningzentren. Ein hohes TC bedingt eben nicht automatisch
auch ein hohes jC.
Fast alle Hochtemperatur Supraleiter sind aus chemischen Stoffen
aufgebaut die aussergewöhnlich giftig sind. Die steigende Giftigkeit
könnte man sogar mit der steigender Sprungtemperatur korrelieren
(Abb. 8.50). Für viele Materialien (z.B. Hg- oder Tl-Verbindungen)
ist die Giftigkeit so gross, dass die Anwendungsmöglichkeiten mit
Sicherheit auch in Zukunft eingeschränkt werden.
Abb. 8.50:
LD50- Giftdosis in mg per kg des
Körpers, welche tödlich für 50% der
Population ist. Ausgerechnet auf
Grund der Daten für die Metalloxyden
222
Ingenieurkeramik III
Abb. 8.51:
Die wichtigsten Eigenschaften der Hochtemperatur-Supraleiter im Vergleich.
(Angaben gelten für Filme)
Werkstoff
NbTi
Bi-2212
Bi-2223
YBCO
8.8.7
TC
[K]
10
95
110
92
JC (4 K)
[A/cm2]
106
5‚105
3‚105
107
JC (77 K)
[A/cm2]
104
5‚104
106
BC2 (4 K)
[T]
14
180
250
150
BC2 (77 K)
[T]
0.1
1
20
Herstellung
Die Herstellungsverfahren der keramischen Supraleiter werden
unterschieden nach der Geometrie des Endproduktes. Wir
unterscheiden Dünnfilme, Dickfilme, Drähte (Bänder) oder
Massivteile. Hierbei werden die verschiedensten bereits bekannten
Methoden angewendet von denen die wichtigsten in der Folge kurz
skizziert werden.
Für das Abscheiden von Dünnfilmen (< 1 μm) hat sich als technisch
wichtigstes Verfahren das IBAD (ion beam assisted deposition)
erwiesen. Das Endprodukt ist ein mehrschichtiger Composite (Abb.
8.52): Als Ausgangssubstrat wird eine Nickelbasis-Legierung
verwendet, die für die nötige mechanische Stabilität sorgt. Darauf
wird nun eine Zirkonoxidschicht (YSZ) abgeschieden, die durch einen
zusätzlichen zweiten Ionenstrahl biaxial (in 2 Richtungen)
ausgerichtet wird, dieser Schritt ist das eigentliche IBAD mit dem eine
perfekt texturierte YSZ-Schicht erhalten wird. Diese entstandene
strenge Textur des YSZ wird vom Supraleiter übernommen, der
mittels einer herkömmlichen Laserabscheidung aufgetragen wird.
Abb. 8.52:
YBCO-Dünnfilm, hergestellt mittels des IBAD-Prozesess.
Ingenieurkeramik III
223
Abb. 8.53:
Temperatur-Zeit Schema des
Schmelzprozessierens mit anschliessendem Glühen.
Dickfilme (10-500μm) werden bevorzugt im Foliengiessverfahren
hergestellt. Die aus einem ethanolhaltigen Schlicker gegossenen
Supraleiter-Folien werden anschliessend auf einem Substrat (Silber
oder Magnesiumoxid) schmelzprozessiert. Dieser Schmelzprozess
gliedert sich in 4 Teile (Abb. 8.53): (1) In der Ausbrennphase werden
die verbliebenen organischen Bestandteile aus der Folie ausgebrannt.
(2) Beim Aufschmelzen wird der Supraleiter in Fremdphasen,
Sauerstoff und Schmelze zersetzt, wir haben also ein peritektisches
Aufschmelzen. (3) Beim nachfolgenden langsamen Abkühlen wird die
supraleitende Phase wieder auskristallisiert. Dies geschieht mit sehr
langsamen Abkühlgeschwindigkeiten von 5-10°C/h um das
Zusammenkommen von Fremdphasen, Sauerstoff und Schmelze zu
ermöglichen.
(4)
Durch
Nachglühen
in
geeigneter
Sauerstoffatmosphäre
schliesslich
wird
die
ideale
Sauerstoffstöchiometrie im Supraleiter eingestellt um optimale
elektrische Eigenschaften zu erreichen. Dieser Schmelzprozess wird
für sämtliche Dickfilme, Drähte und Massivteile verwendet.
Abb. 8.54:
Kritische Stromdichte nehmen für Bi-2212 Filme mit der Dicke ab. Der gesamte
Strom der durch ein Film fliessen kann (per cm der Breite) nimmt aber zu.
Drähte rsp. Bänder werden mittels des sogenannten Powder-in-tube
(PIT) Verfahrens hergestellt. Wie wir im nächsten Kapitel sehen
werden ist es für viele Anwendungen Voraussetzung, dass die spröde
supraleitende Keramik auf Spulen gewickelt werden kann. Da dies mit
224
Ingenieurkeramik III
blosser Keramik niemals möglich ist wird ein gut verformbares
Substrat benötigt. Silber hat sich dafür als einziger Werkstoff tauglich
gezeigt, da es inert gegen die äusserst aggressive Schmelze ist. In
Abb. 8.55 ist der Prozess skizziert: In einem ersten Schritt wird das
vorkalzinierte Supraleiterpulver in feine Silberröhrchen abgefüllt und
zugeschweisst. Mehrere dieser gefüllten Röhrchen werden dann
möglichst dicht zu einem Stack zusammengefügt, der nun aus
mehreren Filamenten besteht. Anschliessend wird der gesamte Stack
während dem Schmelzprozessieren extrudiert und gewalzt wodurch
ein sogenannter Multifilamentleiter entsteht. Beim Walzen und
Extrudieren werden die Körner des Materials orientiert um die
„Weak-links“ zu vermindern. Am Schluss wird wie bei den
Dickfilmen geglüht.
Abb. 8.55:
Schema des Powder-in-tube Prozesses (PIT).
Die kritischen Stromdichten die man in Drahten und Bänder erreicht
werden ständig erhöht (Abb. 8.56). Es ist aber weiterhin sehr
schwierig die hohen Werte für lange (z.B. 1 km) Leiter zu bekommen.
Abb. 8.56:
Entwicklung
der
kritischen
Stromdichte während der neunziger
Jahre.
Massivmaterial schliesslich wird vor oder während dem
Schmelzprozess
mechanisch
oder
durch
Zentrifugalkräfte
zusammengepresst.
Ingenieurkeramik III
225
8.9 Anwendungen
8.9.1
Übersicht
Supraleiter sind in verschiedensten Gebieten der Technik und der
Naturwissenschaften einsetzbar. Sie ermöglichen durch den
Nullwiderstand und den Meissner-Effekt neuartige Geräte
(Strombegrenzer, Energiespeicher, Hochfeldmagnete) oder machen
bestehende Geräte effizienter (Transformatoren, Kabel, Motoren).
Durch die hohen Herstellungs-, Material- und Kühlkosten, konnten
sich bis jetzt jedoch nur einige wenige Anwendungen für Supraleiter
kommerziell durchsetzen. Heliumgekühlte Tieftemperatursupraleiter
(intermetallische Verbindungen) werden eingesetzt als Magnete in
Teilchenbeschleunigern, NMR-Tomographen oder SQUIDs zur
Messung kleinster Magnetfelder. Von den vielen möglichen
Anwendungen für die keramischen Hochtemperatursupraleiter sind bis
heute (1999) einzig die Stromzuführungen vom Normalleiter zum
Tieftemperatursupraleiter von kommerziellem Nutzen.
Für die folgenden Anwendungen wurde die technologische
Machbarkeit bereits demonstriert, viele Anwendungen wurden auch
schon als Prototypen eingesetzt, sie sind aber allesamt noch zu teuer
für eine kommerzielle Nutzung.
Medizin & Wissenschaft:
• MRI (magnetic resonance imaging, NMR)
Das Prinzip liegt daran, dass die Atomkerne mit Spin ≠0 (z.B. H in
H2O) magnetische Momente besitzen. Diese können in grossen
Magnetfeldern beobachtet werden.
• Hochfeldmagnete in Teilchenbeschleunigern
• SQUID (superconducting quantum interference device) zur
Messung kleinster Magnetfelder
Supraleitender Ring (∅ < 1 mm) mit zwei Josephsonkontakten. Bei
niedrigen Temperaturen fliesst im Ring ein supraleitender Strom.
Nach der Quantentheorie dürfen sich im Ring nur eine ganzzahlige
Anzahl magnetischer Flussquanten befinden. Im Ausgangszustand ist
das Feld ausserhalb des Rings und das innerhalb des Rings im
Gleichgewicht. Wird das äussere Feld grösser, kann ein Flussquant in
das SQUID-Loch eindringen und das Gleichgewicht der beiden Felder
wird wieder hergestellt. Bei jedem Flussquant-eindringen wird eine
Strom und Spannung Oszillation im Ring beobachtet.
SQUID’s sind noch für Felder empfindlich, die ein Hundertmillionstel
des Erdfeldes betragen.
226
Ingenieurkeramik III
Abb. 8.57:
SQUID (superconducting quantum
interference device).
Elektronik:
•
•
Mikrowellenfilter
Schalt- und Speicherelemente
Mikrochips: SFQL (Single Flux Quantum
mit einem Flussquantum repräsentiert den
0. Eine Änderung des Zustands gibt ein
Bereich, 10-12 s). Dadurch sind sehr
möglich.
Logic)Supraleitender Ring
logischen Zustand 1, ohne
Spannung Signal (im mV
hohe Schaltungsfrequenz
Abb. 8.58:
Entwicklung der Uhrfrequenz für
Logische Schaltelemente
Industrie:
• Magnetische Lager
Ein Rotor (a flywheel) in der Vakuumkammer als Energiespeicher,
gelagert mit einem magnetischen (HTSL) Lager
• Magnetische Abschirmungen
• MagLev-Züge (magnetic levitation)
Ingenieurkeramik III
227
Abb. 8.59:
Flywheel
Energie:
• Motoren & Generatoren
• SMES (superconducting magnetic
kurzfristigen Energiespeicherung
energy
storage)
zur
Es speichert elektrische Energie im Magnetfeld, das von einer
supraleitenden Spule produziert wird.
•
Unterirdische Übertragungskabel
Abb. 8.60:
SMES Prinzip
Abb. 8.62:
Ein supraleitender Überttragungskabel
Abb. 8.61:
SMES Prototyp
Abb. 8.63:
Ein Durchschnitt eines supraleitenden Band.
Man sieht viele Filamente aus dem
supraleitendem Material im Silbermantel.
228
Ingenieurkeramik III
•
•
Transformatoren
Strombegrenzer
Zweck eines Strombegrenzers ist es, auf zu hohe Ströme oder
Spannungen, verursacht z.B. durch ein Kurzschluss, zu reagieren und
die überschüssige Energie zu absorbieren. Dadurch werden
Kraftwerke untereinander, Fabriken oder einzelne Transformatoren
und Generatoren geschützt, vergleichbar mit Haushaltssicherungen im
Grossformat. Nach ihrer Wirkungsweise werden 2 verschiedene Arten
von Strombegrenzern unterschieden. Der resistive Strombegrenzer
reagiert über die kritische Stromdichte und der induktive
Strombegrenzer über das kritische Magnetfeld auf einen Überstrom.
Abb. 8.64:
Resistiver Strombegrenzer
Der resistive Strombegrenzer ist sehr einfach aufgebaut (Abb. 8.64).
Der Supraleiter wird mit dem zu schützenden Stromkreis in Serie
geschaltet und in flüssigem Stickstoff gekühlt. Im Normalbetrieb
entstehen im System wegen dem Nullwiderstand (nur bei
Gleichstrom!) nur Energieverluste durch die Kühlung. Erhöht sich nun
die Stromdichte durch einen Kurzschluss auf einen Wert oberhalb von
jC, so tritt sofort Normalleitung auf und die überschüssige Energie des
Kurzschlusses wird im Strombegrenzer in Wärme umgewandelt.
Dadurch sinkt die Stromdichte und es tritt wieder Supraleitung ein
womit der Normalbetrieb wieder hergestellt wird, ohne dass etwas
ersetzt werden muss. Um möglichst viel Energie aufnehmen zu
können ohne dass der Supraleiter beschädigt wird, muss die zu
absorbierende Energie auf einen möglichst langen Leiter verteilt
werden, weshalb der Supraleiter meanderförmig auf ein Substrat
prozessiert wird.
Ingenieurkeramik III
Beim induktiven Strombegrenzer wird der zu schützende
Stromkreis über eine Induktionsspule geleitet, deren Selbstinduktion
dem sich ändernden Strom entgegenwirkt. Die Selbstinduktion ist nun
proportional abhängig von der Permeabilität des Materials im Innern
der Spule. Sie ist deshalb mit einem Eisenkern ca. 100‘000fach höher
als mit Luft. Im induktiven Strombegrenzer wird nun der Eisenkern
durch einen Supraleiter, der wiederum mit flüssigem Stickstoff
gekühlt wird, abgeschirmt (Meissner-Effekt). Im Normalbetrieb wird
somit die Selbstinduktion tief gehalten, da das vom Strom induzierte
Magnetfeld den Supraleiter nicht durchdringen und damit das Eisen
nicht magnetisieren kann. Im Schadensfall jedoch erhöht sich das
induzierte Magnetfeld auf einen Wert grösser als das BC des
Supraleiters, dadurch erfolgt sofort die Magnetisierung des Eisens und
ein resultierender Anstieg der Selbstinduktion um das 100‘000fache.
Somit wird ein grosser Teil der überschüssigen Energie vom Eisen
absorbiert. Durch das sich ändernde Magnetfeld werden zudem im
zerstörten Supraleiter Ströme angeworfen. Durch die derart
entstehende induzierte Spannung über der Spule wird der Überstrom
begrenzt. Sobald der Strom absinkt stellt sich wieder der
Ausgangszustand ein.
Abb. 8.65:
Induktiver Strombegrenzer
Literatur
•
•
•
W. Buckel, „Supraleitung“.
VCH Verlagsgesellschaft, Weinheim, 1990.
Bourdillon and N.X. Tan Bourdillon, „High Temperature
Superconductors: Processing and Science“.
San Diego, Academic Press, Inc., 1994.
T.P. Sheahen, „Introduction to High-temperature
Superconductivity“.
Plenum Press, New York and London, 1994.
229