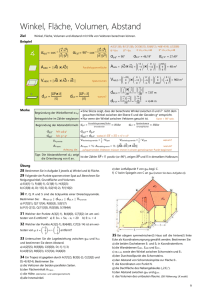
Winkel eines Dreiecks

2-dimensionale Vektorrechnung
Dreiecke
Winkel eines Dreiecks:
Gegeben sind die Punkte A, B und C eines Dreiecks. Berechne die Winkel α, β und γ.
Lösungsweg:
α ist der Winkel zwischen den Vektoren AB und AC :
1. AB =B-A
2. AC =C-A
3. cosα=
AB ⋅ AC
AB ⋅ AC
β ist der Winkel zwischen den Vektoren BA und BC :
4. BA =A-B
5. BC =C-B
6. cosβ=
BA ⋅ BC
BA ⋅ BC
γ ist der Winkel zwischen den Vektoren CA und CB :
7. CA =A-C
8. CB =B-C
9. cosγ =
CA ⋅ CB
CA ⋅ CB
Gerechnetes Beispiel:
A(-1|1), B(2|7) und C(3|-1) bilden ein Dreieck. Berechne die Innenwinkel des
Dreiecks.
Lösung:
Um den Winkel α zu bestimmen, berechnet man zuerst die Vektoren AB und AC :
 2   − 1  3 
AB =B-A=   -   =  
7  1  6
 3   − 1  4 
AC =C-A=   -   =  
 −1  1   − 2 
 3  4 
 . 
AB ⋅ AC
3.4 + 6.(−2)
6  − 2
cosα=
=
=
=0 ⇒ α=90°
3² + 6² . 4² + (−2)²
45. 20
AB ⋅ AC
Um den Winkel β zu bestimmen, berechnet man zuerst die Vektoren BA und BC :
www.matheprofi.at
2-dimensionale Vektorrechnung
Dreiecke
 − 1  2   − 3 
BA =A-B=   -   =  
 1   7   − 6
 3   2  1 
BC =C-B=   -   =  
 −1  7   − 8 
 − 3  1 
 . 
BA ⋅ BC
− 3.1 + (−6).(−8)
 − 6   − 8
cosβ=
=
=
=0,832 ⇒ β=33,69°
(−3)² + (−6)² . 1² + (−8)²
45. 65
BA ⋅ BC
Um den Winkel γ zu bestimmen, berechnet man zuerst die Vektoren CA und CB :
 − 1  3   − 4 
CA =A-C=   -   =  
 1   −1  2 
 2   3   − 1
CB =B-C=   -   =  
 7   −1  8 
 − 4   − 1
 . 
CA ⋅ CB
(−4).(−1) + 2.8
 2  8 
cosγ =
=
=
=0,983 ⇒ γ=56,31°
(−4)² + 2² . (−1)² + 8²
20 . 65
CA ⋅ CB
Hinweis 1: Da die Winkelsumme eines Dreiecks 180° beträgt, kann man den dritten
Winkel berechnen, indem man von 180° die beiden zuerst berechneten Winkel abzieht:
γ=180°-α-β=180°-90°-33,69°=56,31°
Hinweis 2: Um einen Innenwinkel eines Dreiecks oder eines Vierecks berechnen zu
können muss man entweder die beiden Richtungsvektoren verwenden die vom
entsprechenden Eckpunkt wegzeigen, oder die beiden Vektoren die zum Eckpunkt
hinzeigen. Um den Winkel β zu berechnen verwendet man also entweder die Vektoren
BA und BC , oder aber die Vektoren AB und CB . Mit den Vektoren AB und BC
würde man den Winkel 180°-β als Ergebnis erhalten.
www.matheprofi.at