Magnetische Eigenschaften und Raman

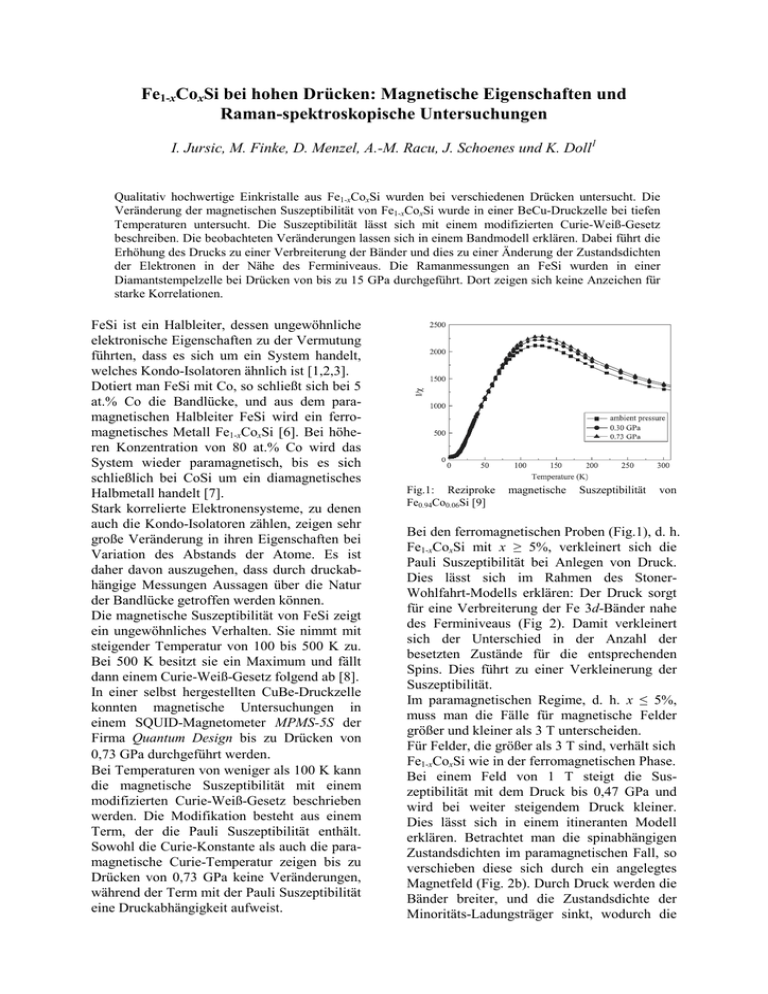
Fe1-xCoxSi bei hohen Drücken: Magnetische Eigenschaften und
Raman-spektroskopische Untersuchungen
I. Jursic, M. Finke, D. Menzel, A.-M. Racu, J. Schoenes und K. Doll1
Qualitativ hochwertige Einkristalle aus Fe1-xCoxSi wurden bei verschiedenen Drücken untersucht. Die
Veränderung der magnetischen Suszeptibilität von Fe1-xCoxSi wurde in einer BeCu-Druckzelle bei tiefen
Temperaturen untersucht. Die Suszeptibilität lässt sich mit einem modifizierten Curie-Weiß-Gesetz
beschreiben. Die beobachteten Veränderungen lassen sich in einem Bandmodell erklären. Dabei führt die
Erhöhung des Drucks zu einer Verbreiterung der Bänder und dies zu einer Änderung der Zustandsdichten
der Elektronen in der Nähe des Ferminiveaus. Die Ramanmessungen an FeSi wurden in einer
Diamantstempelzelle bei Drücken von bis zu 15 GPa durchgeführt. Dort zeigen sich keine Anzeichen für
starke Korrelationen.
FeSi ist ein Halbleiter, dessen ungewöhnliche
elektronische Eigenschaften zu der Vermutung
führten, dass es sich um ein System handelt,
welches Kondo-Isolatoren ähnlich ist [1,2,3].
Dotiert man FeSi mit Co, so schließt sich bei 5
at.% Co die Bandlücke, und aus dem paramagnetischen Halbleiter FeSi wird ein ferromagnetisches Metall Fe1-xCoxSi [6]. Bei höheren Konzentration von 80 at.% Co wird das
System wieder paramagnetisch, bis es sich
schließlich bei CoSi um ein diamagnetisches
Halbmetall handelt [7].
Stark korrelierte Elektronensysteme, zu denen
auch die Kondo-Isolatoren zählen, zeigen sehr
große Veränderung in ihren Eigenschaften bei
Variation des Abstands der Atome. Es ist
daher davon auszugehen, dass durch druckabhängige Messungen Aussagen über die Natur
der Bandlücke getroffen werden können.
Die magnetische Suszeptibilität von FeSi zeigt
ein ungewöhnliches Verhalten. Sie nimmt mit
steigender Temperatur von 100 bis 500 K zu.
Bei 500 K besitzt sie ein Maximum und fällt
dann einem Curie-Weiß-Gesetz folgend ab [8].
In einer selbst hergestellten CuBe-Druckzelle
konnten magnetische Untersuchungen in
einem SQUID-Magnetometer MPMS-5S der
Firma Quantum Design bis zu Drücken von
0,73 GPa durchgeführt werden.
Bei Temperaturen von weniger als 100 K kann
die magnetische Suszeptibilität mit einem
modifizierten Curie-Weiß-Gesetz beschrieben
werden. Die Modifikation besteht aus einem
Term, der die Pauli Suszeptibilität enthält.
Sowohl die Curie-Konstante als auch die paramagnetische Curie-Temperatur zeigen bis zu
Drücken von 0,73 GPa keine Veränderungen,
während der Term mit der Pauli Suszeptibilität
eine Druckabhängigkeit aufweist.
Fig.1: Reziproke
Fe0.94Co0.06Si [9]
magnetische
Suszeptibilität
von
Bei den ferromagnetischen Proben (Fig.1), d. h.
Fe1-xCoxSi mit x ≥ 5%, verkleinert sich die
Pauli Suszeptibilität bei Anlegen von Druck.
Dies lässt sich im Rahmen des StonerWohlfahrt-Modells erklären: Der Druck sorgt
für eine Verbreiterung der Fe 3d-Bänder nahe
des Ferminiveaus (Fig 2). Damit verkleinert
sich der Unterschied in der Anzahl der
besetzten Zustände für die entsprechenden
Spins. Dies führt zu einer Verkleinerung der
Suszeptibilität.
Im paramagnetischen Regime, d. h. x ≤ 5%,
muss man die Fälle für magnetische Felder
größer und kleiner als 3 T unterscheiden.
Für Felder, die größer als 3 T sind, verhält sich
Fe1-xCoxSi wie in der ferromagnetischen Phase.
Bei einem Feld von 1 T steigt die Suszeptibilität mit dem Druck bis 0,47 GPa und
wird bei weiter steigendem Druck kleiner.
Dies lässt sich in einem itineranten Modell
erklären. Betrachtet man die spinabhängigen
Zustandsdichten im paramagnetischen Fall, so
verschieben diese sich durch ein angelegtes
Magnetfeld (Fig. 2b). Durch Druck werden die
Bänder breiter, und die Zustandsdichte der
Minoritäts-Ladungsträger sinkt, wodurch die
Suszeptibilität zunächst ansteigt, ebenso wie
deren Beitrag zur negativen Suszeptibilität.
Bei noch höheren Drücken wird das Band der
Majoritäts-Ladungsträger depopuliert, und die
Zustandsdichte der Minoritäts-Ladungsträger
am Ferminiveau sinkt. Beides führt zu einer
Verkleinerung der Suszeptibilität.
Erhöht man den Druck auf die Probe, so
erhöhen sich die Frequenzen der Phononen. Es
zeigt sich kein außergewöhnliches Verhalten
bei FeSi, welches auf stark korrelierte
Elektronen hinweist.
DFT-Rechnungen für verschiedene Gitterkonstanten und damit verschiedene Drücke
ergeben eine sehr gute qualitative Übereinstimmung. Dies unterstützt die Beschreibungen im itineranten Bild.
Fig.2: Zustandsdichte für Spin-up und Spin-down
Elektronen bei a) paramagnetischer Grundzustand b) in
einem Magnetfeld c) niedrigem Druck d) hohem Druck.
FeSi, Fe1-xCoxSi und CoSi kristallisieren in der
B20-Struktur. Die Faktorgruppenanalyse sagt
voraus, dass für diese Struktur 9 Raman-aktive
Moden zu beobachten sind. Dabei handelt es
sich um 2 A-, 2 E-, und 5 T-Moden.
Es wurden Ramanuntersuchungen an FeSi bei
verschiedenen Drücken in einer Diamantstempeldruckzelle (DAC) durchgeführt. Der
Druck wurde dabei mittels der RubinFluoreszenzmethode bestimmt.
In dem Raman-Spektrum von FeSi (Fig. 3)
sind nur 4 der 9 Raman-aktiven Moden zu
beobachten. Es handelt sich dabei um die EModen bei 180 cm-1 und 316 cm-1, sowie um
die T-Moden bei 192 cm-1 und 308 cm-1. Durch
die kleine Probengröße ist das Signal/RauschVerhältnis zu klein, um die schwach ausgeprägten Strukturen beobachten zu können.
Fig. 3: Ramanspektrum von FeSi bei Drücken bis zu
15 GPa
Fig. 4: Linienposition der E-Mode und T-Mode in
Abhängigkeit des Drucks. Kreise, Quadrate: Experiment;
Dreiecke: Ergebnisse der DFT-Rechnungen
Aus der Veränderung der Linienposition
wurde der druckabhängige Grüneisen-Parameter für die E-Mode bei 180 cm-1 bestimmt.
Dieser hat einen Wert von γE1= 1,48. Im
Vergleich zu stark korrelierten SchwereFermionen-Systemen wie z.B. UPt3 (γ = 60) ist
das ein sehr kleiner Wert. Dieser deutliche
Unterschied zu den Schwere-FermionenSystemen spricht gegen sehr starke Korrelationen der Elektronen im FeSi.
1
MPI für Festkörperforschung, Stuttgart
[1] M. Fäth et al., Phys. Rev. B 58, 15483 (1998).
[2] Aeppli and Z. Fisk, Comments on Cond. Mat. Physics
(Gordon and Breach, Science Publishers S.A., United
Kingdom, 1992), vol. 16, pp. 155–165.
[3] Z. Fisk, J. L. Sarrao, S. L. Cooper, P. Nyhus, G. S.
Boebinger, A. Passner, and P. C. Canfield, Physica B 223,
409 (1996).
[4] Tajima, Y. Endoh, J. E. Fischer, and G. Shirane, Phys.
Rev. B 38, 6954 (1988).
[5] Y. Takahashi, J. Phys.: Condens. Matter 9, 2593
(1997).
[6] D. Menzel, D. Zur, and J. Schoenes, J. Magn. Magn.
Mater. 272-276, 130 (2004).
[7] J. H. Wernick et al., Mater. Res. Bull. 7, 1431 (1972).
[8] V. Jaccarino et al., Phys. Rev. 160, 476 (1967).
[9] D. Menzel, M. Finke, T. Donig, A.-M. Racu, J.
Schoenes, Physica B: Condensed Matter 378-380, 718
(2006).