Vorwort

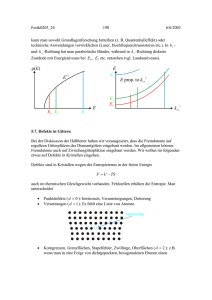
68615778
32
5/14/2016
Man erhält diesen Ausdruck auch im Grenzfall  L   0 :
   L  0 1 
 L2
  L   L  2 L
 02
2.2.2. Quantenmechanische Behandlung
Wir wollen jetzt den Diamagnetismus mit Hilfe der Quantenmechanik herleiten. Dazu
betrachten wir den letzten Term des Hamiltonoperators in Abschnitt 2.1. der 2. Ordnung
in B ist.
Zur Berechnung der freien Energie brauchen wir einen Ausdruck für die
Energieänderung des Grundzustands in einem Magnetfeld. Für B  (0,0, Bz ) erhalten wir
in Störungstheorie 1. Ordnung für den diamagnetischen Anteil
E 
e2 B2
8me
Z

i 1
0 | xi2  yi2 | 0 
e2 B2
8me
Z
2
3 0|r
i 1
i
2
|0 .
Der letzte Schritt gilt nur für gefüllte Elektronenschalen (L = 0, S = 0, J = 0), weil nur
dann die Ladungsverteilung kugelsymmetrisch ist. Aus der Thermodynamik
( dF   SdT  pdV  MdB ) folgt für n Atome pro Volumeneinheit
M 
F
(E )
e2 B Z 2
 n
 n
 ri .
B
B
6me i 1
Damit erhält man für die diamagnetische Suszeptibilität in Störungstheorie 1. Ordnung
einen fast identischen Ausdruck wie in der klassischen Näherung:
 dia
 0 ne 2
M 0M



H
B
6 me
Z

i 1
ri 2 .
In erster Näherung ist  dia wiederum unabhängig von T, da angeregte Zustände n
( n  0 ) meistens nur schwach populiert sind. Meistens setzt man für Z ein Z eff ein, weil
ja nur gefüllte Schalen für den Diamagnetismus relevant sind. Beispiel: Den
Diamagnetismus in Na misst man normalerweise in Salzen wie NaCl, wo Na eine
Edelgaskonfiguration einnimmt.
In welchen Materialien kann man einen starken Diamagnetismus finden?

grosser Radius der Atome, grosses Z:  Xe  43  106 cgs (Fazekas p. 53)
68615778

33
5/14/2016
Moleküle, bei denen sich die Elektronen auf Umlaufbahnen mit grossem Radius
bewegen: Kohlenstoffringe:  graphite  260  10 6 (Alff).
Diese Figur entspricht Figur 2.2 in Blundell.
Falls Elektronenschalen nicht vollständig gefüllt sind, ergeben sich positive Werte für 
( Paramagnetismus), die viel grösser sind als  dia . In Natrium hingegen ist der
Diamagnetismus sehr wichtig:

NaCl:
 para  8  10 6

Na (metallisch):
 dia  2  10 6
2.3. Paramagnetismus
Paramagnetismus tritt in Materialien mit einer ungeraden Zahl von Elektronen immer auf.
Sauerstoff ist aber ein Beispiel eines paramagnetischen Materials mit einer geraden
Anzahl von Elektronen. Paramagnetische Materialien weisen bereits in Nullfeld ein
magnetisches Moment auf, im Gegensatz zu diamagnetischen Materialien, in denen das
Moment durch das äussere Feld induziert wird.
Liegt kein Feld an, zeigen die Momente in willkürliche Richtungen. Bei sehr hohen
Feldern werden alle Momente ausgerichtet und der Körper ist vollständig magnetisiert.
68615778
34
5/14/2016
2.3.1. Klassische Behandlung
Für eine halbklassische Betrachtungsweise verweisen wir auf die Literatur (Blundell p.
23) und die Vorlesung Festkörperphysik. Das Ergebnis lautet:
z
1
 coth( y )   L( y ) .

y
L ( y ) nennt man Langevin-Funktion, y  B /( k BT ) und  z bezeichnet das mittlere
Moment entlang B. Im Grenzfall y  1 erhält man
z
B


3k B T
woraus folgt:
 Langevin  n
0 2
3k B T
.
Das Ergebnis zeigt, das  umgekehrt proportional zu T ist (Curie-Gesetz), was man
auch tatsächlich beobachtet. Die Curie-Konstante C  n 0  2 /(3k B ) ist aber nur korrekt
für „klassische“ Spins, d.h. wenn    B ist. Die klassische Herleitung des
Paramagnetismus liefert trotz des Bohr-van Leeuwen-Theorems eine endliche
Suszeptibilität, weil wir stabile Momente vorausgesetzt haben, die nur existieren können,
wenn wir stabile (d. h. quantisierte) Elektronenbahnen haben.
2.3.2. Quantenmechanische Behandlung: S = ½
Als einfachstes Beispiel betrachten wir ein quantenmechanisches System mit S  12 . Das
magnetische Moment ist gegeben durch
μ   gμ B S .
Legt man ein Magnetfeld an, dann werden 2 Zeeman-Niveaus erzeugt deren Energie
gegeben ist durch (wir setzen g  2.0000)
E  μ  B   B B .
Die Besetzung der zwei möglichen Zustände m1 / 2   12 ist gegeben durch BoltzmannFaktoren exp(  E / k BT ) . Mit der Abkürzung x   B B /( k BT ) erhält man
68615778
35
5/14/2016
N1
N1
ex
2
 x
 N 1 e  e x
2
L
1/2
-B
-1/2
B
2
2BB
N1
2
N1  N 1
2
mJ

x
e
.
e  e x
x
2
1.0
Besetzung des
unteren Zustands
Besetzung
0.8
0.6
0.4
Besetzung des
oberen Zustands
0.2
0.0
0
1
2
x = B/kBT
3
4
File Magnetismus.opj
Die Magnetisierung der Probe ist gerade proportional zur Differenz der beiden Kurven
und man erhält mit N  N  1  N 1
2
2
 B
1
e x  ex
M  ( N  1  N 1 ) B  n  B x
 n B tanh B .
x
2
2
V
k BT
e e
Für x  1 , d.h. hohe Temperaturen ist tanh x  x und man erhält
M  n B
BB
k BT

n B2 B
,
k BT
Für die paramagnetische Suszeptibilität folgt
 para ( S  12 ) 
M  0 M n 0  B2 n 0 g 2  B2 S ( S  1)



.
H
B
k BT
3k B T
 para ( S  12 ) ist 3 mal grösser als das klassische Langevin-Resultat  Langevin  n
0 2
3k B T
!
Für S  12 ist die Abweichung besonders dramatisch, da g 2 S ( S  1)  3  g 2 S 2  1 ist!
68615778
36
5/14/2016
Der Grund liegt darin, dass die transversalen Komponenten eines S  12 Spins sehr gross
sind und zu grossen Nullpunktsfluktuationen führen. Im klassischen Grenzfall mit
S   nähern sich die klassischen und quantenmechanischen Werte an: S (S  1)  S 2 .
100
0.20
Suszeptibilität
80
0.16
0.12
para = C/T
40
-1
para = T/C
20
0
0.08
1/para
para
60
0.04
0
40
80
T (K)
120
0.00
160
File Magnetismus.opj
Den Ausdruck g B S (S  1) bezeichnet man als effektives magnetisches Moment.
Eine viel einfachere Herleitung (Blundell p. 25) ergibt sich, indem man die
Zustandssumme Z  e  B B / k BT  e   B B / k BT  2 cosh(  B B / k BT ) bestimmt und daraus über
die freie Energie direkt die Magnetisierung, spezifische Wärme und die Entropie
berechnet:
68615778
37
5/14/2016
 B
 F 
M  
  n B tanh  B 
 B  T
 k BT 
2
 B
1
 E 
C 
  nk B  B 
2
 T  B
 k B T  (cosh  B B / k B T )

 B
 F 
S  
  nk B ln 2 cosh(  B B / k BT )  - B tanh  B B / k BT  .
k BT
 T  B

]
Die spezifische Wärme weist ein breites Maximum, eine sogenannte Schottky-Anomalie
auf. Diese Form ist typisch für ein System mit zwei Energieniveaus (Tunneling, Gläser
etc.).
Man kann magnetische Momente auf zwei Arten messen:

Suszeptibilität  Curiekonstante   eff  g B S (S  1)

Magnetisierung 
 sat   B
(genauer:  sat  g B S ).
Die Ergebnisse sind wegen den Quantenfluktuationen sehr verschieden! Man muss
immer angeben, welches magnetische Moment man meint.

lokalisierte Momente: man setzt einfach die Quantenzahl S ein, allgemein: J.
68615778

38
5/14/2016
itinerante Momente: da ist sehr viel Physik dahinter (Ni3Al:  sat /  eff  16 ).
Die letztere Frage wird uns insbesondere im Zusammenhang mit der Neutronenstreuung
noch intensive beschäftigen.
2.3.3. Quantenmechanische Behandlung: Allgemeine J
Für beliebige J hat man 2J  1 Niveaus und man erhält für die potentielle Energie E J z
EJz eines Moments mit der z-Komponente des Drehimpulses J
E J z  g B J z B z .
Der g-Faktor ist gegeben durch die Landé-Gleichung (Herleitung: Ashcroft-Mermin p.
797):
g  1
J ( J  1)  S ( S  1)  L( L  1)
.
2 J ( J  1)
Warum ist die Addition von L  S eine einfache Vektoraddition, während die Addition
der Momente zu einem komplizierten g-Faktor führt?
Wie in der folgenden Figur gezeigt ist, ist das magnetische Moment des Spins bereits mit
einem gyromagnetischen Faktor g  2 behaftet, während das orbitale Moment g  1 hat.
Das hat zur Folge, dass das magnetische Moment und der Drehimpuls nicht parallel sind
zueinander.
J
L
S
S
L

68615778
39
5/14/2016
Beachte: Die gezeigte Vektoraddition J  L  S gilt nur für die sogenannte RusselSaunders-Kopplung, in der S, L und J mit dem Hamiltonoperator kommutieren, i.e. gute
Quantenzahlen sind. Sobald die angelegten Felder oder die Spin-Bahn-Kopplung
gross werden, ist dies nicht mehr der Fall. Die Spin-Bahn-Kopplung nimmt typisch mit
Z4 (wasserstoffähnliche Atome) oder Z2 (neutrale Atome, siehe Blundell, Bemerkung 14
p. 35) zu und führt bei den schweren Elementen zur sogenannten jj-Kopplung.
Unter der Annahme, dass die Energie für die angeregten J-Multipletts viel grösser ist als
E J z  g B JB z , erhält man für die Magnetisierung
J
M n
 g
J z  J
B
J ze
J

e
 E J z / k BT
 E J z / k BT
 ng B J
 ( J / J )e
e
aJ z / J
z
aJ z / J
,
J z  J
wobei a  g 0  B JH /( k BT ) . Man sieht, dass der Zähler gerade der Ableitung des
Nenners entspricht und man erhält
M  ng B J
d  J aJ z / J 
.
ln   e

da  J z   J

Dies ist eine geometrische Reihe mit dem Quotienten e  a / J und es ergibt sich durch
Summation und daraus folgende Differentiation der Ausdruck
 g  JH 
 2J  1
 2J  1 1
 a 
 .
M  ng B J 
coth  a
coth    ng B JB j  0 B

 2J  2J
 2 J 
 2J
 k BT 
B J (a ) nennt man die Brillouin-Funktion. Für J 
Resultat B 1 (a )  tanh( a ) .
1
2
erhält man natürlich wieder das
2
Für den Grenzfall kleiner Magnetfelder ( a  1 ) kann man B J (a ) entwickeln und man
erhält
J 1
B J (a) 
a.
3J
Dann gilt für die Magnetisierung
M  ng B J
J  1 g 0  B JH
H
 ng 2  0  B2 J ( J  1)
3J
k BT
3k BT
68615778
40
5/14/2016
und die Suszeptibilität
  ng 2  0  B2 J ( J  1)
n g 2  B2 J ( J  1) n 0 2
H
C
 0

 eff  ,
3k BT
3k B T
3k B T
T
wobei das sogenannte effektive Moment gegeben ist durch
 eff  g B J ( J  1) .
Man erhält damit wiederum das Curie-Gesetz C  T 1 . Im klassischen Grenzfall J  
wird das Resultat von Langevin reproduziert.
Durch Messen der Temperaturabhängigkeit der paramagnetischen Suszeptibilität kann
man  eff eines Materials bestimmen, indem man 1 /  para gegen die Temperatur T
aufträgt. Die Steigung entspricht dann gerade der inversen Curiekonstanten C 1 .
Die folgende Figur nach W. E. Henry, Phys. Rev. 88, 559 (1952) zeigt das magnetische
Moment für die L  0 Ionen



I: Cr3+ ( S  3 / 2 )
II: Fe3+ ( S  5 / 2 )
III: Gd3+ ( S  7 / 2 ).
68615778
41
0
1
5/14/2016
2
3
B/T (T/K)
4
Die Figur zeigt, dass die Sättigungsmagnetisierung für die Ionen gerade den Werten 3, 5
und 7  B entspricht.Die Übereinstimmung der Brillouinfunktion mit dem Experiment ist
sehr gut. Die Steigung bei B / T  0 nimmt mit S zu, weil B / T aufgetragen ist und nicht
SB / T  0 .
2.3.4. Van Vleck Paramagnetismus
Wir haben gesehen, dass der Hamiltonoperator für ein Material in einem Magnetfeld die
folgende Form hat
e2
H  H 0   B (L  gS)  B 
8me
Z
 (B  r )
i 1
2
i
.
Für J  0 ist das Material im Rahmen der Störungstheorie 1. Ordnung unmagnetisch.
Trotzdem kann ein J  0 paramagnetisch sein, wie man bei Anwendung von
Störungstheorie 2. Ordnung feststellt. Die Änderung in der Grundzustandsenergie ist
gegeben durch
E0  0 |  B (L  gS)  B | 0  
n0
0 |  B (L  gS)  B | n
E0  E n
2
e2 B2

8me
Z

i 1
0 | xi2  yi2 | 0 .
Der 1. Term beschreibt im Rahmen der Störungstheorie 1. Ordnung den “normalen”
Paramagnetismus, der 3. Term den Diamagnetismus. Der mittlere Term beschreibt den
68615778
42
5/14/2016
sogenannten Van Vleck Paramagnetismus. Er liefert offensichtlich einen positiven
Beitrag, da E n  E0 angeregte Zustände bezeichnen soll.
Wir betrachten ein einfaches 2-Niveau System mit dem unmagnetischen Grundzustand
|0> und dem angeregten, magnetischen Zustand |1>. Für den Van Vleck Anteil an der
Energieverschiebung erhalten wir
EVV 
0 |  z Bz | 1
E0  E1
2
.
Daraus folgt für die Magnetisierung (   E1  E2 ):
2
2nB z
 | 0 |  z Bz | 1 |
  (F ) 
M  

| 0 |  z | 1 |2
 n

B

B



T
und damit für die (positive) Suszeptibilität
 VV 
2
2
2n 0
  0 | 0 |  z Bz | 1 |

0 | z |1 .
B


VV
Bei nicht zu hohen Temperaturen ist die Van Vleck Suszeptibilität unabhängig von der
Temperatur. Für eine genauere Diskussion siehe Jäger und Perthel p. 20 ff.
Eu2O3
0
100
200
300
T (K)
In der obigen Figur ist die Suszeptibilität für Eu2O3 skizziert. Die Zustände sind gemäss
dem Boltzmann-Faktor besetzt: Bei T = 0 ist nur der Zustand 0 besetzt. Sobald
  k BT wird, nimmt die Suszeptibilität ab, weil die Übergangswahrscheinlichkeit
abnimmt. Bei hohen Temperaturen ist nur der magnetische Zustand 1 besetzt und man
erhält ein Curie-Verhalten.